A company has:
- 100 million ordinary shares outstanding which are trading at a price of $5 each. Market analysts estimated that the company's ordinary stock has a beta of 1.5. The risk-free rate is 5% and the market return is 10%.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant annual dividend of 9% of par. The next dividend will be paid in one year. Assume that all preference dividends will be paid when promised. They currently trade at a price of $90 each.
- Debentures that have a total face value of $200 million and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 110% of their face value.
The corporate tax rate is 30%. All returns and yields are given as effective annual rates.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
In the dividend discount model:
### P_0= \frac{d_1}{r-g} ###
The pronumeral ##g## is supposed to be the:
Question 335 foreign exchange rate, American and European terms
Investors expect Australia's central bank, the RBA, to reduce the policy rate at their next meeting due to fears that the economy is slowing. Then unexpectedly, the policy rate is actually kept unchanged.
What do you expect to happen to Australia's exchange rate?
One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
A stock is expected to pay its next dividend of $1 in one year. Future annual dividends are expected to grow by 2% pa. So the first dividend of $1 will be in one year, the year after that $1.02 (=1*(1+0.02)^1), and a year later $1.0404 (=1*(1+0.02)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
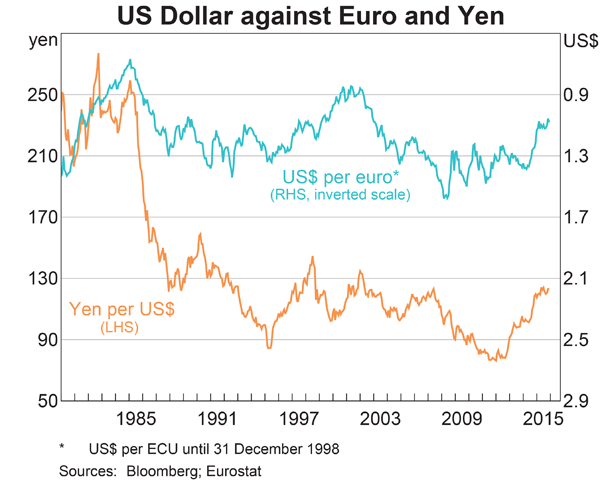
Below is a graph of the USD against the JPY and EUR from 1980 to 2015, compiled by the RBA. Select the correct statement about what occurred between 1980 and 2015. Note that in 1980 the euro was around 1.3 USD per EUR and the Yen was around 250 JPY per USD.
Question 707 continuously compounding rate, continuously compounding rate conversion
Convert a 10% effective annual rate ##(r_\text{eff annual})## into a continuously compounded annual rate ##(r_\text{cc annual})##. The equivalent continuously compounded annual rate is:
Question 744 income and capital returns, real and nominal returns and cash flows, inflation
If someone says "my shares rose by 10% last year", what do you assume that they mean? The effective annual: