For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100) and maturity (3 years).
The only difference is that bond X and Y's yields are 8 and 12% pa respectively. Which of the following statements is true?
Which one of the following bonds is trading at a discount?
Which one of the following bonds is trading at par?
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
Let the 'income return' of a bond be the coupon at the end of the period divided by the market price now at the start of the period ##(C_1/P_0)##. The expected income return of a premium fixed coupon bond is:
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
Your main expense is fuel for your car which costs $100 per month. You just refueled, so you won't need any more fuel for another month (first payment at t=1 month).
You have $2,500 in a bank account which pays interest at a rate of 6% pa, payable monthly. Interest rates are not expected to change.
Assuming that you have no income, in how many months time will you not have enough money to fully refuel your car?
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
What is the net present value (NPV) of undertaking a full-time Australian undergraduate business degree as an Australian citizen? Only include the cash flows over the duration of the degree, ignore any benefits or costs of the degree after it's completed.
Assume the following:
- The degree takes 3 years to complete and all students pass all subjects.
- There are 2 semesters per year and 4 subjects per semester.
- University fees per subject per semester are $1,277, paid at the start of each semester. Fees are expected to remain constant in real terms for the next 3 years.
- There are 52 weeks per year.
- The first semester is just about to start (t=0). The first semester lasts for 19 weeks (t=0 to 19).
- The second semester starts immediately afterwards (t=19) and lasts for another 19 weeks (t=19 to 38).
- The summer holidays begin after the second semester ends and last for 14 weeks (t=38 to 52). Then the first semester begins the next year, and so on.
- Working full time at the grocery store instead of studying full-time pays $20/hr and you can work 35 hours per week. Wages are paid at the end of each week and are expected to remain constant in real terms.
- Full-time students can work full-time during the summer holiday at the grocery store for the same rate of $20/hr for 35 hours per week.
- The discount rate is 9.8% pa. All rates and cash flows are real. Inflation is expected to be 3% pa. All rates are effective annual.
The NPV of costs from undertaking the university degree is:
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Achieve firm free cash flow (FFCF or CFFA) of $1m.
- Pay dividends of $1.8m
- Complete a $1.3m share buy-back.
- Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Read the following financial statements and calculate the firm's free cash flow over the 2014 financial year.
| UBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2014 | ||
| $m | ||
| Sales | 293 | |
| COGS | 200 | |
| Rent expense | 15 | |
| Gas expense | 8 | |
| Depreciation | 10 | |
| EBIT | 60 | |
| Interest expense | 0 | |
| Taxable income | 60 | |
| Taxes | 18 | |
| Net income | 42 | |
| UBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2014 | 2013 |
| $m | $m | |
| Assets | ||
| Cash | 30 | 29 |
| Accounts receivable | 5 | 7 |
| Pre-paid rent expense | 1 | 0 |
| Inventory | 50 | 46 |
| PPE | 290 | 300 |
| Total assets | 376 | 382 |
| Liabilities | ||
| Trade payables | 20 | 18 |
| Accrued gas expense | 3 | 2 |
| Non-current liabilities | 0 | 0 |
| Contributed equity | 212 | 212 |
| Retained profits | 136 | 150 |
| Asset revaluation reserve | 5 | 0 |
| Total L and OE | 376 | 382 |
Note: all figures are given in millions of dollars ($m).
The firm's free cash flow over the 2014 financial year was:
Find the cash flow from assets (CFFA) of the following project.
| One Year Mining Project Data | ||
| Project life | 1 year | |
| Initial investment in building mine and equipment | $9m | |
| Depreciation of mine and equipment over the year | $8m | |
| Kilograms of gold mined at end of year | 1,000 | |
| Sale price per kilogram | $0.05m | |
| Variable cost per kilogram | $0.03m | |
| Before-tax cost of closing mine at end of year | $4m | |
| Tax rate | 30% | |
Note 1: Due to the project, the firm also anticipates finding some rare diamonds which will give before-tax revenues of $1m at the end of the year.
Note 2: The land that will be mined actually has thermal springs and a family of koalas that could be sold to an eco-tourist resort for an after-tax amount of $3m right now. However, if the mine goes ahead then this natural beauty will be destroyed.
Note 3: The mining equipment will have a book value of $1m at the end of the year for tax purposes. However, the equipment is expected to fetch $2.5m when it is sold.
Find the project's CFFA at time zero and one. Answers are given in millions of dollars ($m), with the first cash flow at time zero, and the second at time one.
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.
Which of the below FFCF formulas include the interest tax shield in the cash flow?
###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
Question 413 CFFA, interest tax shield, depreciation tax shield
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA).
One method is to use the following formulas to transform net income (NI) into FFCF including interest and depreciation tax shields:
###FFCF=NI + Depr - CapEx -ΔNWC + IntExp###
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )###
Another popular method is to use EBITDA rather than net income. EBITDA is defined as:
###EBITDA=Rev - COGS - FC###
One of the below formulas correctly calculates FFCF from EBITDA, including interest and depreciation tax shields, giving an identical answer to that above. Which formula is correct?
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
A firm has a debt-to-equity ratio of 60%. What is its debt-to-assets ratio?
Question 241 Miller and Modigliani, leverage, payout policy, diversification, NPV
One of Miller and Modigliani's (M&M's) important insights is that a firm's managers should not try to achieve a particular level of leverage in a world with zero taxes and perfect information since investors can make their own leverage. Therefore corporate capital structure policy is irrelevant since investors can achieve their own desired leverage at the personal level by borrowing or lending on their own.
This principal of 'home-made' or 'do-it-yourself' leverage can also be applied to other topics. Read the following statements to decide which are true:
(I) Payout policy: a firm's managers should not try to achieve a particular pattern of equity payout.
(II) Agency costs: a firm's managers should not try to minimise agency costs.
(III) Diversification: a firm's managers should not try to diversify across industries.
(IV) Shareholder wealth: a firm's managers should not try to maximise shareholders' wealth.
Which of the above statement(s) are true?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?
You may assume:
- the value of debt (D) is constant through time,
- The cost of debt and the yield on debt are equal and given by ##r_D##.
- the appropriate rate to discount interest tax shields is ##r_D##.
- ##\text{IntExp}=D.r_D##
Question 370 capital budgeting, NPV, interest tax shield, WACC, CFFA
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $600k | |
| Depreciation of equipment per year | $250k | |
| Expected sale price of equipment at end of project | $200k | |
| Revenue per job | $12k | |
| Variable cost per job | $4k | |
| Quantity of jobs per year | 120 | |
| Fixed costs per year, paid at the end of each year | $100k | |
| Interest expense in first year (at t=1) | $16.091k | |
| Interest expense in second year (at t=2) | $9.711k | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Levered cost of equity | 12.5% | |
| Market portfolio return | 10% | |
| Beta of assets | 1.24 | |
| Beta of levered equity | 1.5 | |
| Firm's and project's debt-to-equity ratio | 25% | |
Notes
- The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
- Thousands are represented by 'k' (kilo).
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are nominal. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
A young lady is trying to decide if she should attend university or begin working straight away in her home town.
The young lady's grandma says that she should not go to university because she is less likely to marry the local village boy whom she likes because she will spend less time with him if she attends university.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The cost of not marrying the local village boy should be classified as:
Question 559 variance, standard deviation, covariance, correlation
Which of the following statements about standard statistical mathematics notation is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
What is the correlation of a variable X with a constant C?
The corr(X, C) or ##\rho_{X,C}## equals:
The covariance and correlation of two stocks X and Y's annual returns are calculated over a number of years. The units of the returns are in percent per annum ##(\% pa)##.
What are the units of the covariance ##(\sigma_{X,Y})## and correlation ##(\rho_{X,Y})## of returns respectively?
Hint: Visit Wikipedia to understand the difference between percentage points ##(\text{pp})## and percent ##(\%)##.
Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.
What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
The below graph shows a project's net present value (NPV) against its annual discount rate.
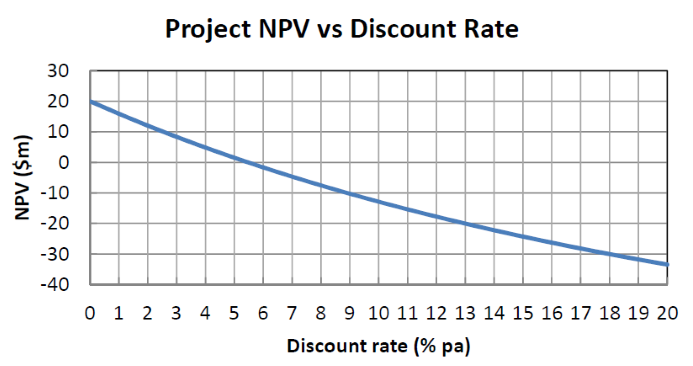
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
Which of the following statements about book and market equity is NOT correct?
Question 443 corporate financial decision theory, investment decision, financing decision, working capital decision, payout policy
Business people make lots of important decisions. Which of the following is the most important long term decision?
The expression 'you have to spend money to make money' relates to which business decision?
This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
Question 535 DDM, real and nominal returns and cash flows, stock pricing
You are an equities analyst trying to value the equity of the Australian telecoms company Telstra, with ticker TLS. In Australia, listed companies like Telstra tend to pay dividends every 6 months. The payment around August is called the final dividend and the payment around February is called the interim dividend. Both occur annually.
- Today is mid-March 2015.
- TLS's last interim dividend of $0.15 was one month ago in mid-February 2015.
- TLS's last final dividend of $0.15 was seven months ago in mid-August 2014.
Judging by TLS's dividend history and prospects, you estimate that the nominal dividend growth rate will be 1% pa. Assume that TLS's total nominal cost of equity is 6% pa. The dividends are nominal cash flows and the inflation rate is 2.5% pa. All rates are quoted as nominal effective annual rates. Assume that each month is exactly one twelfth (1/12) of a year, so you can ignore the number of days in each month.
Calculate the current TLS share price.
Carlos and Edwin are brothers and they both love Holden Commodore cars.
Carlos likes to buy the latest Holden Commodore car for $40,000 every 4 years as soon as the new model is released. As soon as he buys the new car, he sells the old one on the second hand car market for $20,000. Carlos never has to bother with paying for repairs since his cars are brand new.
Edwin also likes Commodores, but prefers to buy 4-year old cars for $20,000 and keep them for 11 years until the end of their life (new ones last for 15 years in total but the 4-year old ones only last for another 11 years). Then he sells the old car for $2,000 and buys another 4-year old second hand car, and so on.
Every time Edwin buys a second hand 4 year old car he immediately has to spend $1,000 on repairs, and then $1,000 every year after that for the next 10 years. So there are 11 payments in total from when the second hand car is bought at t=0 to the last payment at t=10. One year later (t=11) the old car is at the end of its total 15 year life and can be scrapped for $2,000.
Assuming that Carlos and Edwin maintain their love of Commodores and keep up their habits of buying new ones and second hand ones respectively, how much larger is Carlos' equivalent annual cost of car ownership compared with Edwin's?
The real discount rate is 10% pa. All cash flows are real and are expected to remain constant. Inflation is forecast to be 3% pa. All rates are effective annual. Ignore capital gains tax and tax savings from depreciation since cars are tax-exempt for individuals.
You own a nice suit which you wear once per week on nights out. You bought it one year ago for $600. In your experience, suits used once per week last for 6 years. So you expect yours to last for another 5 years.
Your younger brother said that retro is back in style so he wants to wants to borrow your suit once a week when he goes out. With the increased use, your suit will only last for another 4 years rather than 5.
What is the present value of the cost of letting your brother use your current suit for the next 4 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new suit when your current one wears out and your brother will not use the new one; your brother will only use your current suit so he will only use it for the next four years; and the price of a new suit never changes.
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
High risk firms in danger of bankruptcy tend to have:
A firm has a debt-to-equity ratio of 25%. What is its debt-to-assets ratio?
Question 545 income and capital returns, fully amortising loan, no explanation
Which of the following statements about the capital and income returns of a 25 year fully amortising loan asset is correct?
Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.
Over the 25 years from issuance to maturity, a fully amortising loan's expected annual effective:
Question 546 income and capital returns, interest only loan, no explanation
Which of the following statements about the capital and income returns of an interest-only loan is correct?
Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.
An interest-only loan's expected:
Question 760 time calculation, interest only loan, no explanation
Five years ago (##t=-5## years) you entered into an interest-only home loan with a principal of $500,000, an interest rate of 4.5% pa compounding monthly with a term of 25 years.
Then interest rates suddenly fall to 3% pa (##t=0##), but you continue to pay the same monthly home loan payments as you did before. Will your home loan be paid off by the end of its remaining term? If so, in how many years from now? Measure the time taken to pay off the home loan from the current time which is 5 years after the home loan was first entered into.
Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 5, which was the 60th payment since the loan was granted. Also assume that rates were and are expected to remain constant.
Question 800 leverage, portfolio return, risk, portfolio risk, capital structure, no explanation
Which of the following assets would you expect to have the highest required rate of return? All values are current market values.
Question 987 interest tax shield, capital structure, debt terminology
What creates interest tax shields for a company?
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which of the following statements is NOT equivalent to the yield on debt?
Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.
You deposit money into a bank. Which of the following statements is NOT correct? You:
Question 207 income and capital returns, bond pricing, coupon rate, no explanation
For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?
Let: ##P_0## be the bond price now,
##F_T## be the bond's face value,
##T## be the bond's maturity in years,
##r_\text{total}## be the bond's total yield,
##r_\text{income}## be the bond's income yield,
##r_\text{capital}## be the bond's capital yield, and
##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.
A 30 year Japanese government bond was just issued at par with a yield of 1.7% pa. The fixed coupon payments are semi-annual. The bond has a face value of $100.
Six months later, just after the first coupon is paid, the yield of the bond increases to 2% pa. What is the bond's new price?
On 22-Mar-2013 the Australian Government issued series TB139 treasury bonds with a combined face value $23.4m, listed on the ASX with ticker code GSBG25.
The bonds mature on 21-Apr-2025, the fixed coupon rate is 3.25% pa and coupons are paid semi-annually on the 21st of April and October of each year. Each bond's face value is $1,000.
At market close on Friday 11-Sep-2015 the bonds' yield was 2.736% pa.
At market close on Monday 14-Sep-2015 the bonds' yield was 2.701% pa. Both yields are given as annualised percentage rates (APR's) compounding every 6 months. For convenience, assume 183 days in 6 months and 366 days in a year.
What was the historical total return over those 3 calendar days between Friday 11-Sep-2015 and Monday 14-Sep-2015?
There are 183 calendar days from market close on the last coupon 21-Apr-2015 to the market close of the next coupon date on 21-Oct-2015.
Between the market close times from 21-Apr-2015 to 11-Sep-2015 there are 143 calendar days. From 21-Apr-2015 to 14-Sep-2015 there are 146 calendar days.
From 14-Sep-2015 there were 20 coupons remaining to be paid including the next one on 21-Oct-2015.
All of the below answers are given as effective 3 day rates.
A 4.5% fixed coupon Australian Government bond was issued at par in mid-April 2009. Coupons are paid semi-annually in arrears in mid-April and mid-October each year. The face value is $1,000. The bond will mature in mid-April 2020, so the bond had an original tenor of 11 years.
Today is mid-September 2015 and similar bonds now yield 1.9% pa.
What is the bond's new price? Note: there are 10 semi-annual coupon payments remaining from now (mid-September 2015) until maturity (mid-April 2020); both yields are given as APR's compounding semi-annually; assume that the yield curve was flat before the change in yields, and remained flat afterwards as well.
Question 25 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 2 year zero coupon bond at a yield of 8% pa, and a
- 3 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 108 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 1 year zero coupon bond at a yield of 10% pa, and
- A 2 year zero coupon bond at a yield of 8% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Which of the following statements about yield curves is NOT correct?
Question 693 boot strapping zero coupon yield, forward interest rate, term structure of interest rates
Information about three risk free Government bonds is given in the table below.
| Federal Treasury Bond Data | ||||
| Maturity | Yield to maturity | Coupon rate | Face value | Price |
| (years) | (pa, compounding semi-annually) | (pa, paid semi-annually) | ($) | ($) |
| 0.5 | 3% | 4% | 100 | 100.4926 |
| 1 | 4% | 4% | 100 | 100.0000 |
| 1.5 | 5% | 4% | 100 | 98.5720 |
Based on the above government bonds' yields to maturity, which of the below statements about the spot zero rates and forward zero rates is NOT correct?
Here's the Dividend Discount Model, used to price stocks:
### p_0=\frac{d_1}{r-g} ###
All rates are effective annual rates and the cash flows (##d_1##) are received every year. Note that the r and g terms in the above DDM could also be labelled: ###r = r_{\text{total, 0}\rightarrow\text{1yr, eff 1yr}}### ###g = r_{\text{capital, 0}\rightarrow\text{1yr, eff 1yr}}### Which of the following statements is NOT correct?
The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):
###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###
Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:
###r_\text{total}=r_\text{income}+r_\text{capital}###
So the total return of an asset is the income component plus the capital or price growth component.
Another way to break up total return is to use the Capital Asset Pricing Model:
###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###
###r_\text{total}=r_\text{time value}+r_\text{risk premium}###
So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.
Using the above theory and your general knowledge, which of the below equations, if any, are correct?
(I) ##r_\text{income}=r_\text{time value}##
(II) ##r_\text{income}=r_\text{risk premium}##
(III) ##r_\text{capital}=r_\text{time value}##
(IV) ##r_\text{capital}=r_\text{risk premium}##
(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##
Which of the equations are correct?
A company's shares just paid their annual dividend of $2 each.
The stock price is now $40 (just after the dividend payment). The annual dividend is expected to grow by 3% every year forever. The assumptions of the dividend discount model are valid for this company.
What do you expect the effective annual dividend yield to be in 3 years (dividend yield from t=3 to t=4)?
Two years ago Fred bought a house for $300,000.
Now it's worth $500,000, based on recent similar sales in the area.
Fred's residential property has an expected total return of 8% pa.
He rents his house out for $2,000 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $23,173.86.
The future value of 12 months of rental payments one year ahead is $25,027.77.
What is the expected annual growth rate of the rental payments? In other words, by what percentage increase will Fred have to raise the monthly rent by each year to sustain the expected annual total return of 8%?
Question 455 income and capital returns, payout policy, DDM, market efficiency
A fairly priced unlevered firm plans to pay a dividend of $1 next year (t=1) which is expected to grow by 3% pa every year after that. The firm's required return on equity is 8% pa.
The firm is thinking about reducing its future dividend payments by 10% so that it can use the extra cash to invest in more projects which are expected to return 8% pa, and have the same risk as the existing projects. Therefore, next year's dividend will be $0.90. No new equity or debt will be issued to fund the new projects, they'll all be funded by the cut in dividends.
What will be the stock's new annual capital return (proportional increase in price per year) if the change in payout policy goes ahead?
Assume that payout policy is irrelevant to firm value (so there's no signalling effects) and that all rates are effective annual rates.
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
Question 730 DDM, income and capital returns, no explanation
A stock’s current price is $1. Its expected total return is 10% pa and its long term expected capital return is 4% pa. It pays an annual dividend and the next one will be paid in one year. All rates are given as effective annual rates. The dividend discount model is thought to be a suitable model for the stock. Ignore taxes. Which of the following statements about the stock is NOT correct?
In the dividend discount model (DDM), share prices fall when dividends are paid. Let the high price before the fall be called the peak, and the low price after the fall be called the trough.
###P_0=\dfrac{C_1}{r-g}###
Which of the following statements about the DDM is NOT correct?
A share’s current price is $60. It’s expected to pay a dividend of $1.50 in one year. The growth rate of the dividend is 0.5% pa and the stock’s required total return is 3% pa. The stock’s price can be modeled using the dividend discount model (DDM):
##P_0=\dfrac{C_1}{r-g}##
Which of the following methods is NOT equal to the stock’s expected price in one year and six months (t=1.5 years)? Note that the symbolic formulas shown in each line below do equal the formulas with numbers. The formula is just repeated with symbols and then numbers in case it helps you to identify the incorrect statement more quickly.
Question 744 income and capital returns, real and nominal returns and cash flows, inflation
If someone says "my shares rose by 10% last year", what do you assume that they mean? The effective annual:
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
The hardest and most important aspect of business project valuation is the estimation of the:
A zero coupon bond that matures in 6 months has a face value of $1,000.
The firm that issued this bond is trying to forecast its income statement for the year. It needs to calculate the interest expense of the bond this year.
The bond is highly illiquid and hasn't traded on the market. But the finance department have assessed the bond's fair value to be $950 and this is its book value right now at the start of the year.
Assume that:
- the firm uses the 'effective interest method' to calculate interest expense.
- the market value of the bond is the same as the book value.
- the firm is only interested in this bond's interest expense. Do not include the interest expense for a new bond issued to refinance the current one, as would normally happen.
What will be the interest expense of the bond this year for the purpose of forecasting the income statement?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
Which of the following statements is NOT correct? An inverted US government bond yield curve indicates that:
Question 397 financial distress, leverage, capital structure, NPV
A levered firm has a market value of assets of $10m. Its debt is all comprised of zero-coupon bonds which mature in one year and have a combined face value of $9.9m.
Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.
Therefore the current market capitalisation of debt ##(D_0)## is $9m and equity ##(E_0)## is $1m.
A new project presents itself which requires an investment of $2m and will provide a:
- $6.6m cash flow with probability 0.5 in the good state of the world, and a
- -$4.4m (notice the negative sign) cash flow with probability 0.5 in the bad state of the world.
The project can be funded using the company's excess cash, no debt or equity raisings are required.
What would be the new market capitalisation of equity ##(E_\text{0, with project})## if shareholders vote to proceed with the project, and therefore should shareholders proceed with the project?
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
Question 798 idiom, diversification, market efficiency, sunk cost, no explanation
The following quotes are most closely related to which financial concept?
- “Opportunity is missed by most people because it is dressed in overalls and looks like work” -Thomas Edison
- “The only place where success comes before work is in the dictionary” -Vidal Sassoon
- “The safest way to double your money is to fold it over and put it in your pocket” - Kin Hubbard
The expression 'cash is king' emphasizes the importance of having enough cash to pay your short term debts to avoid bankruptcy. Which business decision is this expression most closely related to?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in four and a half years (t = 4.5)?
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.
What is the implied growth rate of the dividend per year?
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
Stocks in the United States usually pay quarterly dividends. For example, the retailer Wal-Mart Stores paid a $0.47 dividend every quarter over the 2013 calendar year and plans to pay a $0.48 dividend every quarter over the 2014 calendar year.
Using the dividend discount model and net present value techniques, calculate the stock price of Wal-Mart Stores assuming that:
- The time now is the beginning of January 2014. The next dividend of $0.48 will be received in 3 months (end of March 2014), with another 3 quarterly payments of $0.48 after this (end of June, September and December 2014).
- The quarterly dividend will increase by 2% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in 2015 will be $0.4896 (##=0.48×(1+0.02)^1##), with the first at the end of March 2015 and the last at the end of December 2015. In 2016 each quarterly dividend will be $0.499392 (##=0.48×(1+0.02)^2##), with the first at the end of March 2016 and the last at the end of December 2016, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- All cash flows and rates are nominal. Inflation is 3% pa.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
The first payment of a constant perpetual annual cash flow is received at time 5. Let this cash flow be ##C_5## and the required return be ##r##.
So there will be equal annual cash flows at time 5, 6, 7 and so on forever, and all of the cash flows will be equal so ##C_5 = C_6 = C_7 = ...##
When the perpetuity formula is used to value this stream of cash flows, it will give a value (V) at time:
A very low-risk stock just paid its semi-annual dividend of $0.14, as it has for the last 5 years. You conservatively estimate that from now on the dividend will fall at a rate of 1% every 6 months.
If the stock currently sells for $3 per share, what must be its required total return as an effective annual rate?
If risk free government bonds are trading at a yield of 4% pa, given as an effective annual rate, would you consider buying or selling the stock?
The stock's required total return is:
Select the most correct statement from the following.
'Chartists', also known as 'technical traders', believe that:
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
A project to build a toll road will take 3 years to complete, costing three payments of $50 million, paid at the start of each year (at times 0, 1, and 2).
After completion, the toll road will yield a constant $10 million at the end of each year forever with no costs. So the first payment will be at t=4.
The required return of the project is 10% pa given as an effective nominal rate. All cash flows are nominal.
What is the payback period?
In Australia, domestic university students are allowed to buy concession tickets for the bus, train and ferry which sell at a discount of 50% to full-price tickets.
The Australian Government do not allow international university students to buy concession tickets, they have to pay the full price.
Some international students see this as unfair and they are willing to pay for fake university identification cards which have the concession sticker.
What is the most that an international student would be willing to pay for a fake identification card?
Assume that international students:
- consider buying their fake card on the morning of the first day of university from their neighbour, just before they leave to take the train into university.
- buy their weekly train tickets on the morning of the first day of each week.
- ride the train to university and back home again every day seven days per week until summer holidays 40 weeks from now. The concession card only lasts for those 40 weeks. Assume that there are 52 weeks in the year for the purpose of interest rate conversion.
- a single full-priced one-way train ride costs $5.
- have a discount rate of 11% pa, given as an effective annual rate.
Approach this question from a purely financial view point, ignoring the illegality, embarrassment and the morality of committing fraud.
Question 65 annuity with growth, needs refinement
Which of the below formulas gives the present value of an annuity with growth?
Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###
The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.
The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.
###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###
The equation of a perpetuity with growth is:
###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###A company has:
- 10 million common shares outstanding, each trading at a price of $90.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant dividend of 9% of par. They currently trade at a price of $120 each.
- Debentures that have a total face value of $60,000,000 and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 90% of their face value.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts estimate that the company's common stock has a beta of 1.2. The corporate tax rate is 30%.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
A text book publisher is thinking of asking some teachers to write a new textbook at a cost of $100,000, payable now. The book would be written, printed and ready to sell to students in 2 years. It will be ready just before semester begins.
A cash flow of $100 would be made from each book sold, after all costs such as printing and delivery. There are 600 students per semester. Assume that every student buys a new text book. Remember that there are 2 semesters per year and students buy text books at the beginning of the semester.
Assume that text book publishers will sell the books at the same price forever and that the number of students is constant.
If the discount rate is 8% pa, given as an effective annual rate, what is the NPV of the project?
A student just won the lottery. She won $1 million in cash after tax. She is trying to calculate how much she can spend per month for the rest of her life. She assumes that she will live for another 60 years. She wants to withdraw equal amounts at the beginning of every month, starting right now.
All of the cash is currently sitting in a bank account which pays interest at a rate of 6% pa, given as an APR compounding per month. On her last withdrawal, she intends to have nothing left in her bank account. How much can she withdraw at the beginning of each month?
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
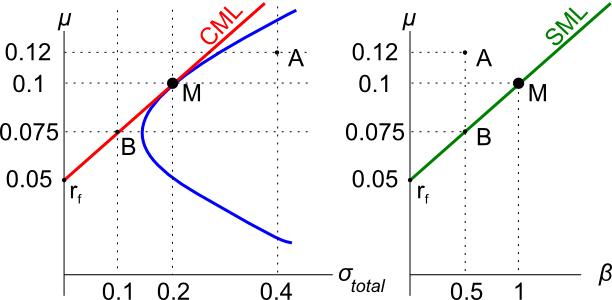
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
The CAPM can be used to find a business's expected opportunity cost of capital:
###r_i=r_f+β_i (r_m-r_f)###
What should be used as the risk free rate ##r_f##?
Question 418 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $8m | |
| Depreciation of equipment per year | $8m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 4m | |
| Sale price per unit | $10 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense in first year (at t=1) | $0.562m | |
| Corporate tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 9% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.32 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-equity ratio | 50% | |
Notes
- Due to the project, current assets will increase by $6m now (t=0) and fall by $6m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa. All rates are given as effective annual rates.
- The project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
The efficient markets hypothesis (EMH) and no-arbitrage pricing theory are most closely related to which of the following concepts?
Question 494 franking credit, personal tax on dividends, imputation tax system
A firm pays a fully franked cash dividend of $100 to one of its Australian shareholders who has a personal marginal tax rate of 15%. The corporate tax rate is 30%.
What will be the shareholder's personal tax payable due to the dividend payment?
A pharmaceutical firm has just discovered a valuable new drug. So far the news has been kept a secret.
The net present value of making and commercialising the drug is $200 million, but $600 million of bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and bond raising to shareholders simultaneously in the same announcement. The bonds will be issued shortly after.
Once the announcement is made and the bonds are issued, what is the expected increase in the value of the firm's assets (ΔV), market capitalisation of debt (ΔD) and market cap of equity (ΔE)?
The triangle symbol is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##ΔV = ΔD+ΔE##
Question 513 stock split, reverse stock split, stock dividend, bonus issue, rights issue
Which of the following statements is NOT correct?
In mid 2009 the listed mining company Rio Tinto announced a 21-for-40 renounceable rights issue. Below is the chronology of events:
- 04/06/2009. Share price opens at $69.00 and closes at $66.90.
- 05/06/2009. 21-for-40 rights issue announced at a subscription price of $28.29.
- 16/06/2009. Last day that shares trade cum-rights. Share price opens at $76.40 and closes at $75.50.
- 17/06/2009. Shares trade ex-rights. Rights trading commences.
All things remaining equal, what would you expect Rio Tinto's stock price to open at on the first day that it trades ex-rights (17/6/2009)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
Question 448 franking credit, personal tax on dividends, imputation tax system
A small private company has a single shareholder. This year the firm earned a $100 profit before tax. All of the firm's after tax profits will be paid out as dividends to the owner.
The corporate tax rate is 30% and the sole shareholder's personal marginal tax rate is 45%.
The Australian imputation tax system applies because the company generates all of its income in Australia and pays corporate tax to the Australian Tax Office. Therefore all of the company's dividends are fully franked. The sole shareholder is an Australian for tax purposes and can therefore use the franking credits to offset his personal income tax liability.
What will be the personal tax payable by the shareholder and the corporate tax payable by the company?
Question 710 continuously compounding rate, continuously compounding rate conversion
A continuously compounded monthly return of 1% ##(r_\text{cc monthly})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.
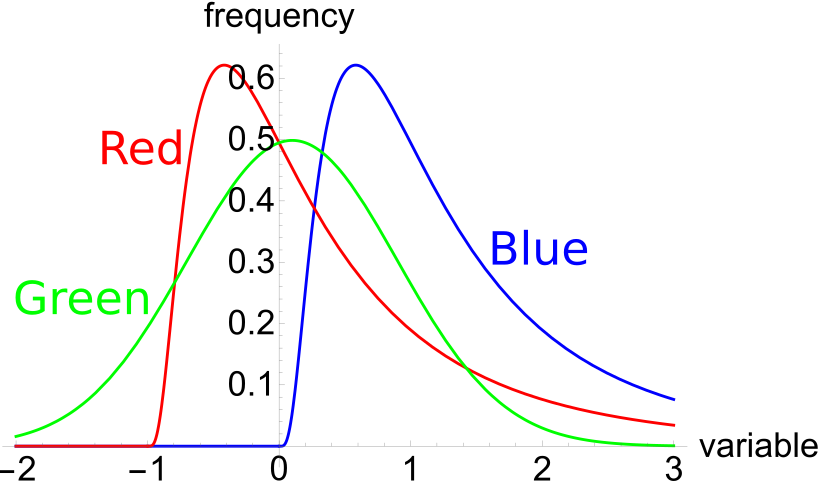
Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 926 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the median dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Question 927 mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the mean dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Question 319 foreign exchange rate, monetary policy, American and European terms
Investors expect the Reserve Bank of Australia (RBA) to keep the policy rate steady at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 25 basis points due to fears that the economy is growing too fast and that inflation will be above their target rate of 2 to 3 per cent.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:
The Chinese government attempts to fix its exchange rate against the US dollar and at the same time use monetary policy to fix its interest rate at a set level.
To be able to fix its exchange rate and interest rate in this way, what does the Chinese government actually do?
- Adopts capital controls to prevent financial arbitrage by private firms and individuals.
- Adopts the same interest rate (monetary policy) as the United States.
- Fixes inflation so that the domestic real interest rate is equal to the United States' real interest rate.
Which of the above statements is or are true?
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Profitability Index (PI) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?