A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
Three years ago Frederika bought a house for $400,000.
Now it's worth $600,000, based on recent similar sales in the area.
Frederika's residential property has an expected total return of 7% pa.
She rents her house out for $2,500 per month, paid in advance. Every 12 months she plans to increase the rental payments.
The present value of 12 months of rental payments is $29,089.48.
The future value of 12 months of rental payments one year ahead is $31,125.74.
What is the expected annual capital yield of the property?
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
An Indonesian lady wishes to convert 1 million Indonesian rupiah (IDR) to Australian dollars (AUD). Exchange rates are 13,125 IDR per USD and 0.79 USD per AUD. How many AUD is the IDR 1 million worth?
The symbol ##\text{GDR}_{0\rightarrow 1}## represents a stock's gross discrete return per annum over the first year. ##\text{GDR}_{0\rightarrow 1} = P_1/P_0##. The subscript indicates the time period that the return is mentioned over. So for example, ##\text{AAGDR}_{1 \rightarrow 3}## is the arithmetic average GDR measured over the two year period from years 1 to 3, but it is expressed as a per annum rate.
Which of the below statements about the arithmetic and geometric average GDR is NOT correct?
Question 817 expected and historical returns, income and capital returns
Over the last year, a constant-dividend-paying stock's price fell, while it's future expected dividends and profit remained the same. Assume that:
- Now is ##t=0##, last year is ##t=-1## and next year is ##t=1##;
- The dividend is paid at the end of each year, the last dividend was just paid today ##(C_0)## and the next dividend will be paid next year ##(C_1)##;
- Markets are efficient and the dividend discount model is suitable for valuing the stock.
Which of the following statements is NOT correct? The stock's:
Suppose the current Australian exchange rate is 0.8 USD per AUD.
If you think that the AUD will appreciate against the USD, contrary to the rest of the market, how could you profit? Right now you should:
Question 977 comparative advantage in trade, production possibilities curve, no explanation
Arthur and Bindi are the only people on a remote island. Their production possibility curves are shown in the graph.
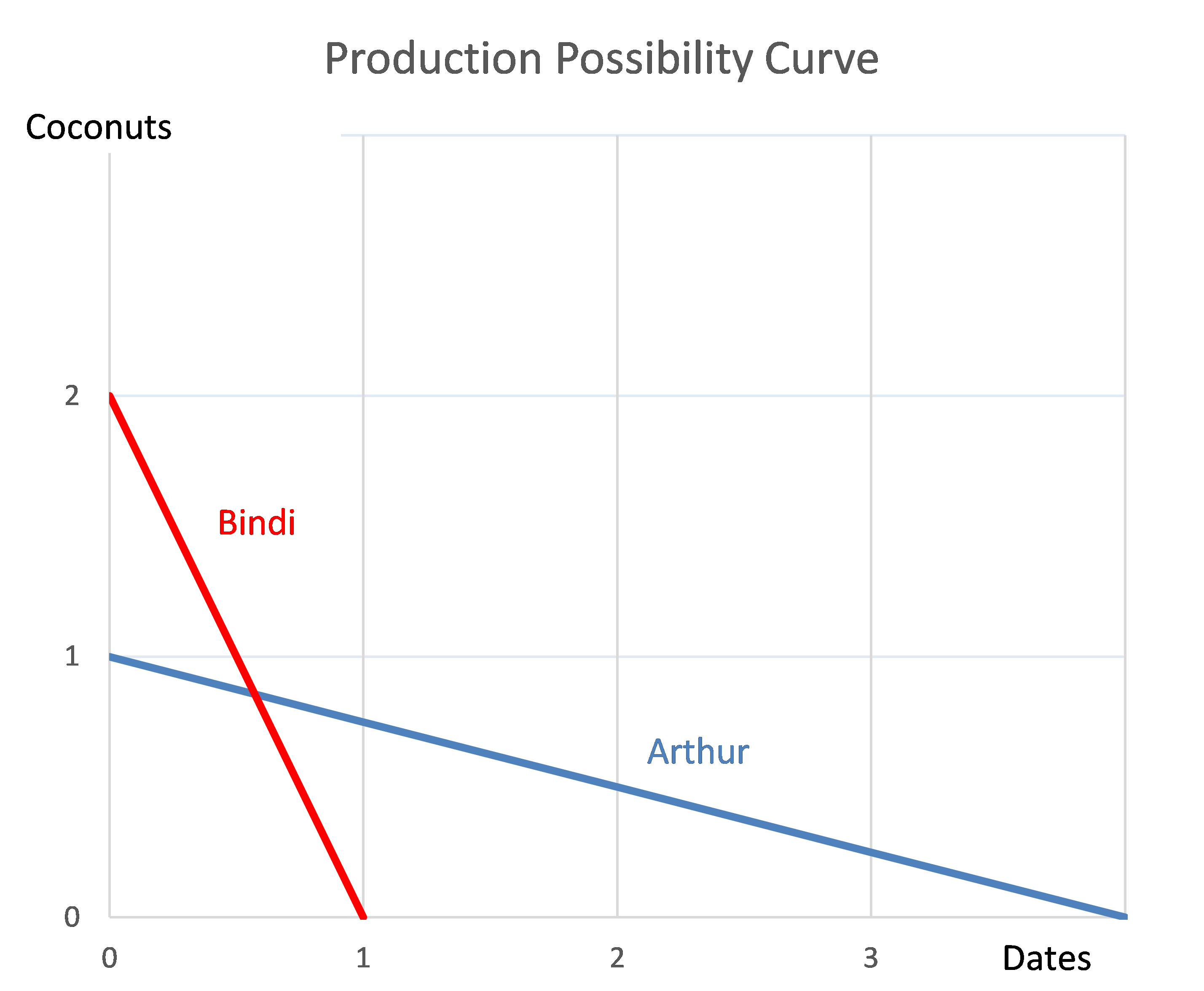
Which of the following statements is NOT correct?