The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_{0} = \frac{c_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What is the discount rate '## r_\text{eff} ##' in this equation?
A furniture distributor offers credit to its customers. Customers are given 25 days to pay for their goods, but if they pay immediately they will get a 1% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay either immediately or on the 25th day. All rates given below are effective annual rates.
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0 | 6 | 12 | 18 | 20 | ... |
After year 4, the dividend will grow in perpetuity at 5% pa. The required return of the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
If all of the dividends since time period zero were deposited into a bank account yielding 8% pa as an effective annual rate, how much money will be in the bank account in 2.5 years (in other words, at t=2.5)?
The current gold price is $700, gold storage costs are 2% pa and the risk free rate is 10% pa, both with continuous compounding.
What should be the 3 year gold futures price?
Question 668 buy and hold, market efficiency, idiom
A quote from the famous investor Warren Buffet: "Much success can be attributed to inactivity. Most investors cannot resist the temptation to constantly buy and sell."
Buffet is referring to the buy-and-hold strategy which is to buy and never sell shares. Which of the following is a disadvantage of a buy-and-hold strategy? Assume that share markets are semi-strong form efficient. Which of the following is NOT an advantage of the strict buy-and-hold strategy? A disadvantage of the buy-and-hold strategy is that it reduces:
Question 834 option, delta, theta, gamma, standard deviation, Black-Scholes-Merton option pricing
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
| European Call Option | ||
| on a non-dividend paying stock | ||
| Description | Symbol | Quantity |
| Spot price ($) | ##S_0## | 20 |
| Strike price ($) | ##K_T## | 18 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.3 |
| Option maturity (years) | ##T## | 1 |
| Call option price ($) | ##c_0## | 3.939488 |
| Delta | ##\Delta = N[d_1]## | 0.747891 |
| ##N[d_2]## | ##N[d_2]## | 0.643514 |
| Gamma | ##\Gamma## | 0.053199 |
| Theta ($/year) | ##\Theta = \partial c / \partial T## | 1.566433 |
Question 862 yield curve, bond pricing, bill pricing, monetary policy, no explanation
Refer to the below graph when answering the questions.
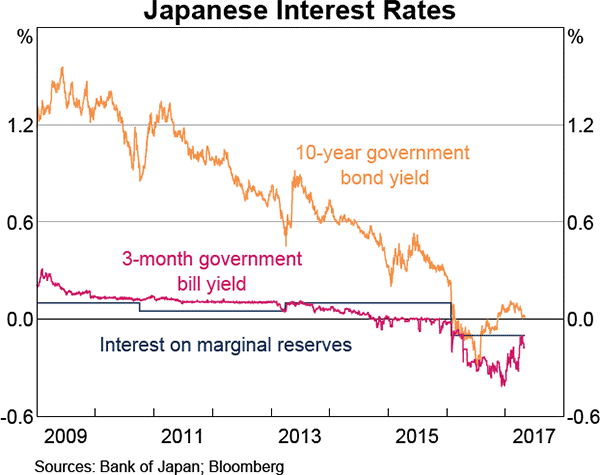
Which of the following statements is NOT correct?
Which of the following statements about bond convexity is NOT correct?
A common phrase heard in financial markets is that ‘high risk investments deserve high returns’. To make this statement consistent with the Capital Asset Pricing Model (CAPM), a high amount of what specific type of risk deserves a high return?
Investors deserve high returns when they buy assets with high: