Question 180 equivalent annual cash flow, inflation, real and nominal returns and cash flows
Details of two different types of light bulbs are given below:
- Low-energy light bulbs cost $3.50, have a life of nine years, and use about $1.60 of electricity a year, paid at the end of each year.
- Conventional light bulbs cost only $0.50, but last only about a year and use about $6.60 of energy a year, paid at the end of each year.
The real discount rate is 5%, given as an effective annual rate. Assume that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the Equivalent Annual Cost (EAC) of the low-energy and conventional light bulbs. The below choices are listed in that order.
An industrial chicken farmer grows chickens for their meat. Chickens:
- Cost $0.50 each to buy as chicks. They are bought on the day they’re born, at t=0.
- Grow at a rate of $0.70 worth of meat per chicken per week for the first 6 weeks (t=0 to t=6).
- Grow at a rate of $0.40 worth of meat per chicken per week for the next 4 weeks (t=6 to t=10) since they’re older and grow more slowly.
- Feed costs are $0.30 per chicken per week for their whole life. Chicken feed is bought and fed to the chickens once per week at the beginning of the week. So the first amount of feed bought for a chicken at t=0 costs $0.30, and so on.
- Can be slaughtered (killed for their meat) and sold at no cost at the end of the week. The price received for the chicken is their total value of meat (note that the chicken grows fast then slow, see above).
The required return of the chicken farm is 0.5% given as an effective weekly rate.
Ignore taxes and the fixed costs of the factory. Ignore the chicken’s welfare and other environmental and ethical concerns.
Find the equivalent weekly cash flow of slaughtering a chicken at 6 weeks and at 10 weeks so the farmer can figure out the best time to slaughter his chickens. The choices below are given in the same order, 6 and 10 weeks.
You're advising your superstar client 40-cent who is weighing up buying a private jet or a luxury yacht. 40-cent is just as happy with either, but he wants to go with the more cost-effective option. These are the cash flows of the two options:
- The private jet can be bought for $6m now, which will cost $12,000 per month in fuel, piloting and airport costs, payable at the end of each month. The jet will last for 12 years.
- Or the luxury yacht can be bought for $4m now, which will cost $20,000 per month in fuel, crew and berthing costs, payable at the end of each month. The yacht will last for 20 years.
What's unusual about 40-cent is that he is so famous that he will actually be able to sell his jet or yacht for the same price as it was bought since the next generation of superstar musicians will buy it from him as a status symbol.
Bank interest rates are 10% pa, given as an effective annual rate. You can assume that 40-cent will live for another 60 years and that when the jet or yacht's life is at an end, he will buy a new one with the same details as above.
Would you advise 40-cent to buy the or the ?
Note that the effective monthly rate is ##r_\text{eff monthly}=(1+0.1)^{1/12}-1=0.00797414##
Question 249 equivalent annual cash flow, effective rate conversion
Details of two different types of desserts or edible treats are given below:
- High-sugar treats like candy, chocolate and ice cream make a person very happy. High sugar treats are cheap at only $2 per day.
- Low-sugar treats like nuts, cheese and fruit make a person equally happy if these foods are of high quality. Low sugar treats are more expensive at $4 per day.
The advantage of low-sugar treats is that a person only needs to pay the dentist $2,000 for fillings and root canal therapy once every 15 years. Whereas with high-sugar treats, that treatment needs to be done every 5 years.
The real discount rate is 10%, given as an effective annual rate. Assume that there are 365 days in every year and that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the equivalent annual cash flow (EAC) of the high-sugar treats and low-sugar treats, including dental costs. The below choices are listed in that order.
Ignore the pain of dental therapy, personal preferences and other factors.
Question 56 income and capital returns, bond pricing, premium par and discount bonds
Which of the following statements about risk free government bonds is NOT correct?
Hint: Total return can be broken into income and capital returns as follows:
###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###
The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.
Question 210 real estate, inflation, real and nominal returns and cash flows, income and capital returns
Assume that the Gordon Growth Model (same as the dividend discount model or perpetuity with growth formula) is an appropriate method to value real estate.
An old rule of thumb in the real estate industry is that properties should yield a 5% pa rental return. Some investors also regard property to be as risky as the stock market, therefore property is thought to have a required total return of 9% pa which is the average total return on the stock market including dividends.
Assume that all returns are effective annual rates and they are nominal (not reduced by inflation). Inflation is expected to be 2% pa.
You're considering purchasing an investment property which has a rental yield of 5% pa and you expect it to have the same risk as the stock market. Select the most correct statement about this property.
Question 213 income and capital returns, bond pricing, premium par and discount bonds
The coupon rate of a fixed annual-coupon bond is constant (always the same).
What can you say about the income return (##r_\text{income}##) of a fixed annual coupon bond? Remember that:
###r_\text{total} = r_\text{income} + r_\text{capital}###
###r_\text{total, 0 to 1} = \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0}###
Assume that there is no change in the bond's total annual yield to maturity from when it is issued to when it matures.
Select the most correct statement.
From its date of issue until maturity, the income return of a fixed annual coupon:
Question 239 income and capital returns, inflation, real and nominal returns and cash flows, interest only loan
A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.
From the bank's point of view, what is the long term expected nominal capital return of the loan asset?
Question 282 expected and historical returns, income and capital returns
You're the boss of an investment bank's equities research team. Your five analysts are each trying to find the expected total return over the next year of shares in a mining company. The mining firm:
- Is regarded as a mature company since it's quite stable in size and was floated around 30 years ago. It is not a high-growth company;
- Share price is very sensitive to changes in the price of the market portfolio, economic growth, the exchange rate and commodities prices. Due to this, its standard deviation of total returns is much higher than that of the market index;
- Experienced tough times in the last 10 years due to unexpected falls in commodity prices.
- Shares are traded in an active liquid market.
- The analysts' source data is correct and true, but their inferences might be wrong;
- All returns and yields are given as effective annual nominal rates.
Question 415 income and capital returns, real estate, no explanation
You just bought a residential apartment as an investment property for $500,000.
You intend to rent it out to tenants. They are ready to move in, they would just like to know how much the monthly rental payments will be, then they will sign a twelve-month lease.
You require a total return of 8% pa and a rental yield of 5% pa.
What would the monthly paid-in-advance rental payments have to be this year to receive that 5% annual rental yield?
Also, if monthly rental payments can be increased each year when a new lease agreement is signed, by how much must you increase rents per year to realise the 8% pa total return on the property?
Ignore all taxes and the costs of renting such as maintenance costs, real estate agent fees, utilities and so on. Assume that there will be no periods of vacancy and that tenants will promptly pay the rental prices you charge.
Note that the first rental payment will be received at t=0. The first lease agreement specifies the first 12 equal payments from t=0 to 11. The next lease agreement can have a rental increase, so the next twelve equal payments from t=12 to 23 can be higher than previously, and so on forever.
Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
A highly levered risky firm is trying to raise more debt. The types of debt being considered, in no particular order, are senior bonds, junior bonds, bank accepted bills, promissory notes and bank loans.
Which of these forms of debt is the safest from the perspective of the debt investors who are thinking of investing in the firm's new debt?
Question 22 NPV, perpetuity with growth, effective rate, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 10% given as an effective annual rate?
The first payment of $90 is in 3 years, followed by payments every 6 months in perpetuity after that which shrink by 3% every 6 months. That is, the growth rate every 6 months is actually negative 3%, given as an effective 6 month rate. So the payment at ## t=3.5 ## years will be ## 90(1-0.03)^1=87.3 ##, and so on.
The phone company Telstra have 2 mobile service plans on offer which both have the same amount of phone call, text message and internet data credit. Both plans have a contract length of 24 months and the monthly cost is payable in advance. The only difference between the two plans is that one is a:
- 'Bring Your Own' (BYO) mobile service plan, costing $50 per month. There is no phone included in this plan. The other plan is a:
- 'Bundled' mobile service plan that comes with the latest smart phone, costing $71 per month. This plan includes the latest smart phone.
Neither plan has any additional payments at the start or end.
The only difference between the plans is the phone, so what is the implied cost of the phone as a present value?
Assume that the discount rate is 2% per month given as an effective monthly rate, the same high interest rate on credit cards.
Question 48 IRR, NPV, bond pricing, premium par and discount bonds, market efficiency
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
In Australia, domestic university students are allowed to buy concession tickets for the bus, train and ferry which sell at a discount of 50% to full-price tickets.
The Australian Government do not allow international university students to buy concession tickets, they have to pay the full price.
Some international students see this as unfair and they are willing to pay for fake university identification cards which have the concession sticker.
What is the most that an international student would be willing to pay for a fake identification card?
Assume that international students:
- consider buying their fake card on the morning of the first day of university from their neighbour, just before they leave to take the train into university.
- buy their weekly train tickets on the morning of the first day of each week.
- ride the train to university and back home again every day seven days per week until summer holidays 40 weeks from now. The concession card only lasts for those 40 weeks. Assume that there are 52 weeks in the year for the purpose of interest rate conversion.
- a single full-priced one-way train ride costs $5.
- have a discount rate of 11% pa, given as an effective annual rate.
Approach this question from a purely financial view point, ignoring the illegality, embarrassment and the morality of committing fraud.
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
Harvey Norman the large retailer often runs sales advertising 2 years interest free when you purchase its products. This offer can be seen as a free personal loan from Harvey Norman to its customers.
Assume that banks charge an interest rate on personal loans of 12% pa given as an APR compounding per month. This is the interest rate that Harvey Norman deserves on the 2 year loan it extends to its customers. Therefore Harvey Norman must implicitly include the cost of this loan in the advertised sale price of its goods.
If you were a customer buying from Harvey Norman, and you were paying immediately, not in 2 years, what is the minimum percentage discount to the advertised sale price that you would insist on? (Hint: if it makes it easier, assume that you’re buying a product with an advertised price of $100).
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0 | 6 | 12 | 18 | 20 | ... |
After year 4, the dividend will grow in perpetuity at 5% pa. The required return of the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in 7 years (t = 7), just after the dividend at that time has been paid?
A very low-risk stock just paid its semi-annual dividend of $0.14, as it has for the last 5 years. You conservatively estimate that from now on the dividend will fall at a rate of 1% every 6 months.
If the stock currently sells for $3 per share, what must be its required total return as an effective annual rate?
If risk free government bonds are trading at a yield of 4% pa, given as an effective annual rate, would you consider buying or selling the stock?
The stock's required total return is:
You just started work at your new job which pays $48,000 per year.
The human resources department have given you the option of being paid at the end of every week or every month.
Assume that there are 4 weeks per month, 12 months per year and 48 weeks per year.
Bank interest rates are 12% pa given as an APR compounding per month.
What is the dollar gain over one year, as a net present value, of being paid every week rather than every month?
Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.
What is the net present value (NPV) of borrowing from your friend?
Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the end-of-year amount, paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
How much money do you expect to have in the fund in 40 years? Also, what is the future value of the fees that the fund expects to earn from you? Give both amounts as future values in 40 years. Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
- The fund invests its fees in the same companies as it invests your funds in, but with no fees.
The below answer choices list your expected wealth in 40 years and then the fund's expected wealth in 40 years.
The boss of WorkingForTheManCorp has a wicked (and unethical) idea. He plans to pay his poor workers one week late so that he can get more interest on his cash in the bank.
Every week he is supposed to pay his 1,000 employees $1,000 each. So $1 million is paid to employees every week.
The boss was just about to pay his employees today, until he thought of this idea so he will actually pay them one week (7 days) later for the work they did last week and every week in the future, forever.
Bank interest rates are 10% pa, given as a real effective annual rate. So ##r_\text{eff annual, real} = 0.1## and the real effective weekly rate is therefore ##r_\text{eff weekly, real} = (1+0.1)^{1/52}-1 = 0.001834569##
All rates and cash flows are real, the inflation rate is 3% pa and there are 52 weeks per year. The boss will always pay wages one week late. The business will operate forever with constant real wages and the same number of employees.
What is the net present value (NPV) of the boss's decision to pay later?
A young lady is trying to decide if she should attend university or not.
The young lady's parents say that she must attend university because otherwise all of her hard work studying and attending school during her childhood was a waste.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The hard work studying at school in her childhood should be classified as:
What is the net present value (NPV) of undertaking a full-time Australian undergraduate business degree as an Australian citizen? Only include the cash flows over the duration of the degree, ignore any benefits or costs of the degree after it's completed.
Assume the following:
- The degree takes 3 years to complete and all students pass all subjects.
- There are 2 semesters per year and 4 subjects per semester.
- University fees per subject per semester are $1,277, paid at the start of each semester. Fees are expected to remain constant in real terms for the next 3 years.
- There are 52 weeks per year.
- The first semester is just about to start (t=0). The first semester lasts for 19 weeks (t=0 to 19).
- The second semester starts immediately afterwards (t=19) and lasts for another 19 weeks (t=19 to 38).
- The summer holidays begin after the second semester ends and last for 14 weeks (t=38 to 52). Then the first semester begins the next year, and so on.
- Working full time at the grocery store instead of studying full-time pays $20/hr and you can work 35 hours per week. Wages are paid at the end of each week and are expected to remain constant in real terms.
- Full-time students can work full-time during the summer holiday at the grocery store for the same rate of $20/hr for 35 hours per week.
- The discount rate is 9.8% pa. All rates and cash flows are real. Inflation is expected to be 3% pa. All rates are effective annual.
The NPV of costs from undertaking the university degree is:
Over the next year, the management of an unlevered company plans to:
- Achieve firm free cash flow (FFCF or CFFA) of $1m.
- Pay dividends of $1.8m
- Complete a $1.3m share buy-back.
- Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Over the next year, the management of an unlevered company plans to:
- Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
- Pay dividends of $1m.
- Complete a $1.3m share buy-back.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Question 545 income and capital returns, fully amortising loan, no explanation
Which of the following statements about the capital and income returns of a 25 year fully amortising loan asset is correct?
Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.
Over the 25 years from issuance to maturity, a fully amortising loan's expected annual effective:
You just entered into a fully amortising home loan with a principal of $600,000, a variable interest rate of 4.25% pa and a term of 25 years.
Immediately after settling the loan, the variable interest rate suddenly falls to 4% pa! You can't believe your luck. Despite this, you plan to continue paying the same home loan payments as you did before. How long will it now take to pay off your home loan?
Assume that the lower interest rate was granted immediately and that rates were and are now again expected to remain constant. Round your answer up to the nearest whole month.
Question 546 income and capital returns, interest only loan, no explanation
Which of the following statements about the capital and income returns of an interest-only loan is correct?
Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.
An interest-only loan's expected:
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.
For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
Question 25 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 2 year zero coupon bond at a yield of 8% pa, and a
- 3 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 96 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds paying semi-annual coupons:
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Bonds A and B are issued by the same Australian company. Both bonds yield 7% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond A pays coupons of 10% pa and bond B pays coupons of 5% pa. Which of the following statements is true about the bonds' prices?
Question 572 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Question 573 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, liquidity premium theory, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
A young lady is trying to decide if she should attend university. Her friends say that she should go to university because she is more likely to meet a clever young man than if she begins full time work straight away.
What's the correct way to classify this item from a capital budgeting perspective when trying to find the Net Present Value of going to university rather than working?
The opportunity to meet a desirable future spouse should be classified as:
A man has taken a day off from his casual painting job to relax.
It's the end of the day and he's thinking about the hours that he could have spent working (in the past) which are now:
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
For a price of $102, Andrea will sell you a share which just paid a dividend of $10 yesterday, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##10(1+0.05)^1=$10.50## in one year from now, and the year after it will be ##10(1+0.05)^2=11.025## and so on.
The required return of the stock is 15% pa.
Currently, a mining company has a share price of $6 and pays constant annual dividends of $0.50. The next dividend will be paid in 1 year. Suddenly and unexpectedly the mining company announces that due to higher than expected profits, all of these windfall profits will be paid as a special dividend of $0.30 in 1 year.
If investors believe that the windfall profits and dividend is a one-off event, what will be the new share price? If investors believe that the additional dividend is actually permanent and will continue to be paid, what will be the new share price? Assume that the required return on equity is unchanged. Choose from the following, where the first share price includes the one-off increase in earnings and dividends for the first year only ##(P_\text{0 one-off})## , and the second assumes that the increase is permanent ##(P_\text{0 permanent})##:
Note: When a firm makes excess profits they sometimes pay them out as special dividends. Special dividends are just like ordinary dividends but they are one-off and investors do not expect them to continue, unlike ordinary dividends which are expected to persist.
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
Stocks in the United States usually pay quarterly dividends. For example, the retailer Wal-Mart Stores paid a $0.47 dividend every quarter over the 2013 calendar year and plans to pay a $0.48 dividend every quarter over the 2014 calendar year.
Using the dividend discount model and net present value techniques, calculate the stock price of Wal-Mart Stores assuming that:
- The time now is the beginning of January 2014. The next dividend of $0.48 will be received in 3 months (end of March 2014), with another 3 quarterly payments of $0.48 after this (end of June, September and December 2014).
- The quarterly dividend will increase by 2% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in 2015 will be $0.4896 (##=0.48×(1+0.02)^1##), with the first at the end of March 2015 and the last at the end of December 2015. In 2016 each quarterly dividend will be $0.499392 (##=0.48×(1+0.02)^2##), with the first at the end of March 2016 and the last at the end of December 2016, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- All cash flows and rates are nominal. Inflation is 3% pa.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Assume that there are no dividend payments so the entire 15% total return is all capital return.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% return lasts for the next 100 years (t=0 to 100), then reverts to 10% pa after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant. All returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
Discounted cash flow (DCF) valuation prices assets by finding the present value of the asset's future cash flows. The single cash flow, annuity, and perpetuity equations are very useful for this.
Which of the following equations is the 'perpetuity with growth' equation?
What type of present value equation is best suited to value a residential house investment property that is expected to pay constant rental payments forever? Note that 'constant' has the same meaning as 'level' in this context.
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
Question 339 bond pricing, inflation, market efficiency, income and capital returns
Economic statistics released this morning were a surprise: they show a strong chance of consumer price inflation (CPI) reaching 5% pa over the next 2 years.
This is much higher than the previous forecast of 3% pa.
A vanilla fixed-coupon 2-year risk-free government bond was issued at par this morning, just before the economic news was released.
What is the expected change in bond price after the economic news this morning, and in the next 2 years? Assume that:
- Inflation remains at 5% over the next 2 years.
- Investors demand a constant real bond yield.
- The bond price falls by the (after-tax) value of the coupon the night before the ex-coupon date, as in real life.
A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 3 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
Which of the following statements about book and market equity is NOT correct?
You own some nice shoes which you use once per week on date nights. You bought them 2 years ago for $500. In your experience, shoes used once per week last for 6 years. So you expect yours to last for another 4 years.
Your younger sister said that she wants to borrow your shoes once per week. With the increased use, your shoes will only last for another 2 years rather than 4.
What is the present value of the cost of letting your sister use your current shoes for the next 2 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new pair of shoes when your current pair wears out and your sister will not use the new ones; your sister will only use your current shoes so she will only use it for the next 2 years; and the price of new shoes never changes.
You own a nice suit which you wear once per week on nights out. You bought it one year ago for $600. In your experience, suits used once per week last for 6 years. So you expect yours to last for another 5 years.
Your younger brother said that retro is back in style so he wants to wants to borrow your suit once a week when he goes out. With the increased use, your suit will only last for another 4 years rather than 5.
What is the present value of the cost of letting your brother use your current suit for the next 4 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new suit when your current one wears out and your brother will not use the new one; your brother will only use your current suit so he will only use it for the next four years; and the price of a new suit never changes.
You just bought a nice dress which you plan to wear once per month on nights out. You bought it a moment ago for $600 (at t=0). In your experience, dresses used once per month last for 6 years.
Your younger sister is a student with no money and wants to borrow your dress once a month when she hits the town. With the increased use, your dress will only last for another 3 years rather than 6.
What is the present value of the cost of letting your sister use your current dress for the next 3 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new dress when your current one wears out; your sister will only use the current dress, not the next one that you will buy; and the price of a new dress never changes.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which firms tend to have high forward-looking price-earnings (PE) ratios?
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Question 446 working capital decision, corporate financial decision theory
The working capital decision primarily affects which part of a business?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
The expression 'cash is king' emphasizes the importance of having enough cash to pay your short term debts to avoid bankruptcy. Which business decision is this expression most closely related to?
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
Question 370 capital budgeting, NPV, interest tax shield, WACC, CFFA
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $600k | |
| Depreciation of equipment per year | $250k | |
| Expected sale price of equipment at end of project | $200k | |
| Revenue per job | $12k | |
| Variable cost per job | $4k | |
| Quantity of jobs per year | 120 | |
| Fixed costs per year, paid at the end of each year | $100k | |
| Interest expense in first year (at t=1) | $16.091k | |
| Interest expense in second year (at t=2) | $9.711k | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Levered cost of equity | 12.5% | |
| Market portfolio return | 10% | |
| Beta of assets | 1.24 | |
| Beta of levered equity | 1.5 | |
| Firm's and project's debt-to-equity ratio | 25% | |
Notes
- The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
- Thousands are represented by 'k' (kilo).
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are nominal. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Scubar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 60 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 90 | |
| Taxes at 30% | 27 | |
| Net income | 63 | |
| Scubar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 60 | 50 |
| Trade debtors | 19 | 6 |
| Rent paid in advance | 3 | 2 |
| PPE | 420 | 400 |
| Total assets | 502 | 458 |
| Trade creditors | 10 | 8 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 130 | 130 |
| Retained profits | 162 | 130 |
| Total L and OE | 502 | 458 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
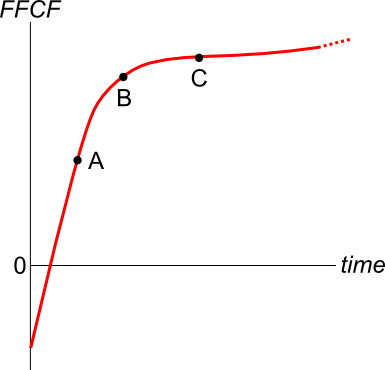
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
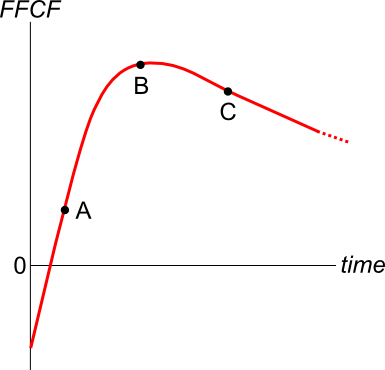
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
The hardest and most important aspect of business project valuation is the estimation of the: