You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
A three year bond has a face value of $100, a yield of 10% and a fixed coupon rate of 5%, paid semi-annually. What is its price?
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
A 180-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A 90-day Bank Accepted Bill (BAB) has a face value of $1,000,000. The simple interest rate is 10% pa and there are 365 days in the year. What is its price now?
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
The below graph shows a project's net present value (NPV) against its annual discount rate.
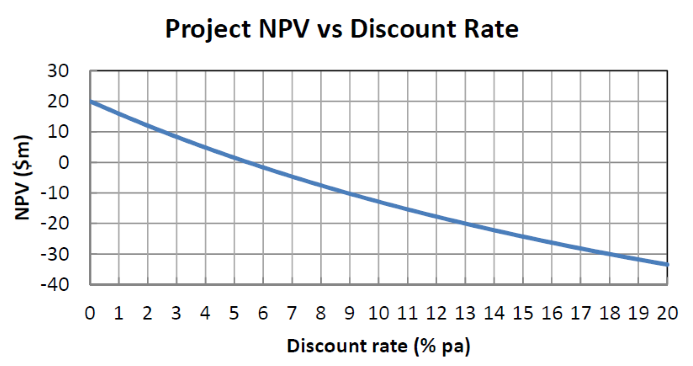
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
A project's net present value (NPV) is negative. Select the most correct statement.
What is the Internal Rate of Return (IRR) of the project detailed in the table below?
Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
You're considering a business project which costs $11m now and is expected to pay a single cash flow of $11m in one year. So you pay $11m now, then one year later you receive $11m.
Assume that the initial $11m cost is funded using the your firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about the net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
A stock is expected to pay its next dividend of $1 in one year. Future annual dividends are expected to grow by 2% pa. So the first dividend of $1 will be in one year, the year after that $1.02 (=1*(1+0.02)^1), and a year later $1.0404 (=1*(1+0.02)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
A stock just paid a dividend of $1. Future annual dividends are expected to grow by 2% pa. The next dividend of $1.02 (=1*(1+0.02)^1) will be in one year, and the year after that the dividend will be $1.0404 (=1*(1+0.02)^2), and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
A share pays annual dividends. It just paid a dividend of $2. The growth rate in the dividend is 3% pa. You estimate that the stock's required return is 8% pa. Both the discount rate and growth rate are given as effective annual rates.
Using the dividend discount model, what is the share price?
A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.
What is the implied growth rate of the dividend per year?
The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
A stock has a beta of 0.5.
In the last 5 minutes, the federal government unexpectedly raised taxes. Over this time the share market fell by 3%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
Question 905 market capitalisation of equity, PE ratio, payout ratio
The below graph shows the computer software company Microsoft's stock price (MSFT) at the market close on the NASDAQ on Friday 1 June 2018.
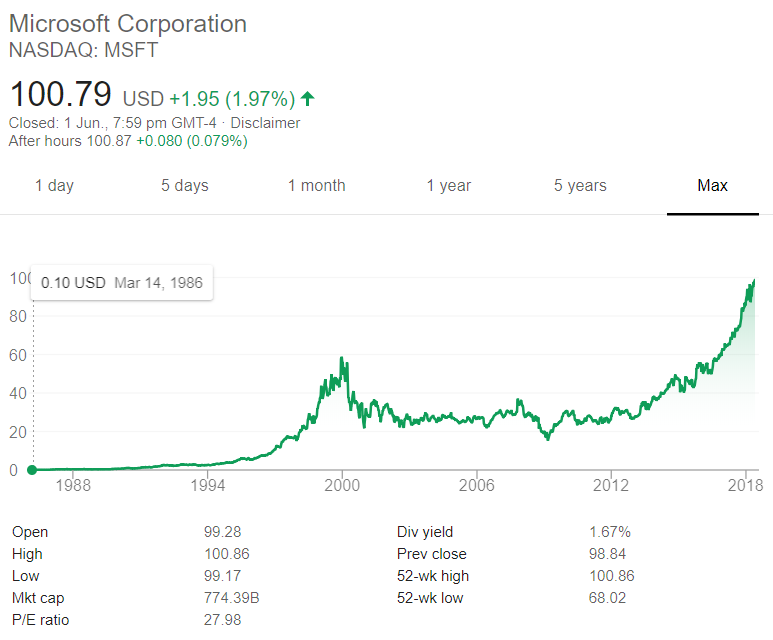
Based on the screenshot above, which of the following statements about MSFT is NOT correct? MSFT's:
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

On 1 February 2016 you were told that your refinery company will need to purchase oil on 1 July 2016. You were afraid of the oil price rising between now and then so you bought some August 2016 futures contracts on 1 February 2016 to hedge against changes in the oil price. On 1 February 2016 the oil price was $40 and the August 2016 futures price was $43.
It's now 1 July 2016 and oil price is $45 and the August 2016 futures price is $46. You bought the spot oil and closed out your futures position on 1 July 2016.
What was the effective price paid for the oil, taking into account basis risk? All spot and futures oil prices quoted above and below are per barrel.
A 12 month European-style call option with a strike price of $11 is written on a dividend paying stock currently trading at $10. The dividend is paid annually and the next dividend is expected to be $0.40, paid in 9 months. The risk-free interest rate is 5% pa continuously compounded and the standard deviation of the stock’s continuously compounded returns is 30 percentage points pa. The stock's continuously compounded returns are normally distributed. Using the Black-Scholes-Merton option valuation model, determine which of the following statements is NOT correct.
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
The price of gold is currently $700 per ounce. The forward price for delivery in 1 year is $800. An arbitrageur can borrow money at 10% per annum given as an effective discrete annual rate. Assume that gold is fairly priced and the cost of storing gold is zero.
What is the best way to conduct an arbitrage in this situation? The best arbitrage strategy requires zero capital, has zero risk and makes money straight away. An arbitrageur should sell 1 forward on gold and:
A one year European-style call option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The call option price now is:
A one year European-style put option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The put option price now is:
A one year European-style call option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
A one year European-style put option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The put option price now is:
Question 794 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the Delta of a European call option?
Where:
###d_1=\dfrac{\ln[S_0/K]+(r+\sigma^2/2).T)}{\sigma.\sqrt{T}}### ###d_2=d_1-\sigma.\sqrt{T}=\dfrac{\ln[S_0/K]+(r-\sigma^2/2).T)}{\sigma.\sqrt{T}}###Question 795 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the Delta of a European put option?
Question 796 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European call option will be exercised?
Question 797 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European put option will be exercised?
You believe that the price of a share will fall significantly very soon, but the rest of the market does not. The market thinks that the share price will remain the same. Assuming that your prediction will soon be true, which of the following trades is a bad idea? In other words, which trade will NOT make money or prevent losses?
A European call option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the call option?
A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the put option?
A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from having written (being short) the put option?
A European call option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from having written (being short) the call option?
Question 432 option, option intrinsic value, no explanation
An American style call option with a strike price of ##K## dollars will mature in ##T## years. The underlying asset has a price of ##S## dollars.
What is an expression for the current intrinsic value in dollars from owning (being long) the American style call option? Note that the intrinsic value of an option does not subtract the premium paid to buy the option.
Which of the following statements about option contracts is NOT correct? For every:
If trader A has sold the right that allows counterparty B to buy the underlying asset from him at maturity if counterparty B wants then trader A is:
After doing extensive fundamental analysis of a company, you believe that their shares are overpriced and will soon fall significantly. The market believes that there will be no such fall.
Which of the following strategies is NOT a good idea, assuming that your prediction is true?
Question 636 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being long a call option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Question 637 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being short a call option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Question 639 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being short a put option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Question 638 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being long a put option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Which one of the below option and futures contracts gives the possibility of potentially unlimited gains?
A trader buys one crude oil European style call option contract on the CME expiring in one year with an exercise price of $44 per barrel for a price of $6.64. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before maturity, then at maturity she will have the:
Which of the below formulas gives the profit ##(\pi)## from being long a call option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LC,0}##. Note that ##S_T##, ##X_T## and ##f_{LC,0}## are all positive numbers.
Which of the below formulas gives the profit ##(\pi)## from being short a call option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LC,0}##. Note that ##S_T##, ##X_T## and ##f_{LC,0}## are all positive numbers.
Which of the below formulas gives the profit ##(\pi)## from being long a put option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LP,0}##. Note that ##S_T##, ##X_T## and ##f_{LP,0}## are all positive numbers.
Which of the below formulas gives the profit ##(\pi)## from being short a put option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LP,0}##. Note that ##S_T##, ##X_T## and ##f_{LP,0}## are all positive numbers.
A trader sells one crude oil European style call option contract on the CME expiring in one year with an exercise price of $44 per barrel for a price of $6.64. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before maturity, then at maturity she will have the:
A trader buys one crude oil European style put option contract on the CME expiring in one year with an exercise price of $44 per barrel for a price of $6.64. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before maturity, then at maturity she will have the:
Which of the following statements about call options is NOT correct?
Below are 4 option graphs. Note that the y-axis is payoff at maturity (T). What options do they depict? List them in the order that they are numbered.
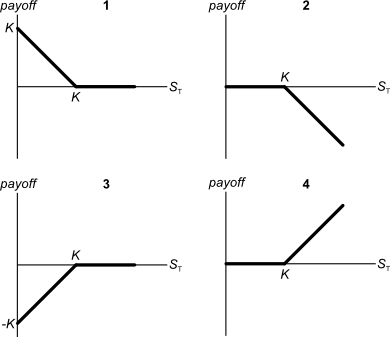
Which of the below formulas gives the payoff at maturity ##(f_T)## from being long a future? Let the underlying asset price at maturity be ##S_T## and the locked-in futures price be ##K_T##.
Which of the below formulas gives the payoff at maturity ##(f_T)## from being short a future? Let the underlying asset price at maturity be ##S_T## and the locked-in futures price be ##K_T##.
A trader buys one crude oil futures contract on the CME expiring in one year with a locked-in futures price of $38.94 per barrel. If the trader doesn’t close out her contract before expiry then in one year she will have the:
A trader sells one crude oil futures contract on the CME expiring in one year with a locked-in futures price of $38.94 per barrel. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before expiry then in one year she will have the:
In general, stock prices tend to rise. What does this mean for futures on equity?
Which of the following statements about futures contracts on shares is NOT correct, assuming that markets are efficient?
When an equity future is first negotiated (at t=0):
The current gold price is $700, gold storage costs are 2% pa and the risk free rate is 10% pa, both with continuous compounding.
What should be the 3 year gold futures price?
A 2-year futures contract on a stock paying a continuous dividend yield of 3% pa was bought when the underlying stock price was $10 and the risk free rate was 10% per annum with continuous compounding. Assume that investors are risk-neutral, so the stock's total required return is the risk free rate.
Find the forward price ##(F_2)## and value of the contract ##(V_0)## initially. Also find the value of the contract in 6 months ##(V_{0.5})## if the stock price rose to $12.
A stock is expected to pay a dividend of $5 per share in 1 month and $5 again in 7 months.
The stock price is $100, and the risk-free rate of interest is 10% per annum with continuous compounding. The yield curve is flat. Assume that investors are risk-neutral.
An investor has just taken a short position in a one year forward contract on the stock.
Find the forward price ##(F_1)## and value of the contract ##(V_0)## initially. Also find the value of the short futures contract in 6 months ##(V_\text{0.5, SF})## if the stock price fell to $90.
A stock is expected to pay its semi-annual dividend of $1 per share for the foreseeable future. The current stock price is $40 and the continuously compounded risk free rate is 3% pa for all maturities. An investor has just taken a long position in a 12-month futures contract on the stock. The last dividend payment was exactly 4 months ago. Therefore the next $1 dividend is in 2 months, and the $1 dividend after is 8 months from now. Which of the following statements about this scenario is NOT correct?
An equity index stands at 100 points and the one year equity futures price is 107.
The equity index is expected to have a dividend yield of 3% pa. Assume that investors are risk-neutral so their total required return on the shares is the same as the risk free Treasury bond yield which is 10% pa. Both are given as discrete effective annual rates.
Assuming that the equity index is fairly priced, an arbitrageur would recognise that the equity futures are:
An equity index stands at 100 points and the one year equity futures price is 102.
The equity index is expected to have a dividend yield of 4% pa. Assume that investors are risk-neutral so their total required return on the shares is the same as the risk free Treasury bond yield which is 10% pa. Both are given as discrete effective annual rates.
Assuming that the equity index is fairly priced, an arbitrageur would recognise that the equity futures are:
In February a company sold one December 40,000 pound (about 18 metric tons) lean hog futures contract. It closed out its position in May.
The spot price was $0.68 per pound in February. The December futures price was $0.70 per pound when the trader entered into the contract in February, $0.60 when he closed out his position in May, and $0.55 when the contract matured in December.
What was the total profit?
A trader just bought a European style put option on CBA stock. The current option premium is $2, the exercise price is $75, the option matures in one year and the spot CBA stock price is $74.
Which of the following statements is NOT correct?
A company runs a number of slaughterhouses which supply hamburger meat to McDonalds. The company is afraid that live cattle prices will increase over the next year, even though there is widespread belief in the market that they will be stable. What can the company do to hedge against the risk of increasing live cattle prices? Which statement(s) are correct?
(i) buy call options on live cattle.
(ii) buy put options on live cattle.
(iii) sell call options on live cattle.
Select the most correct response:
You operate a cattle farm that supplies hamburger meat to the big fast food chains. You buy a lot of grain to feed your cattle, and you sell the fully grown cattle on the livestock market.
You're afraid of adverse movements in grain and livestock prices. What options should you buy to hedge your exposures in the grain and cattle livestock markets?
Select the most correct response:
Question 584 option, option payoff at maturity, option profit
Which of the following statements about European call options on non-dividend paying stocks is NOT correct?
Being long a call and short a put which have the same exercise prices and underlying stock is equivalent to being:
A stock, a call, a put and a bond are available to trade. The call and put options' underlying asset is the stock they and have the same strike prices, ##K_T##.
Being long the call and short the stock is equivalent to being:
A stock, a call, a put and a bond are available to trade. The call and put options' underlying asset is the stock they and have the same strike prices, ##K_T##.
You are currently long the stock. You want to hedge your long stock position without actually trading the stock. How would you do this?
A company can invest funds in a five year project at LIBOR plus 50 basis points pa. The five-year swap rate is 4% pa. What fixed rate of interest can the company earn over the next five years by using the swap?
Question 785 fixed for floating interest rate swap, non-intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 3 | L - 0.4 | ||
| Firm B | 5 | L + 1 | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design a non-intermediated swap that benefits firm A only. What will be the swap rate?
Question 786 fixed for floating interest rate swap, intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 3 | L - 0.4 | ||
| Firm B | 5 | L + 1 | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design an intermediated swap (which means there will actually be two swaps) that nets a bank 0.1% and shares the remaining swap benefits between Firms A and B equally. Which of the following statements about the swap is NOT correct?
Question 787 fixed for floating interest rate swap, intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 2 | L - 0.1 | ||
| Firm B | 2.5 | L | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design an intermediated swap (which means there will actually be two swaps) that nets a bank 0.15% and grants the remaining swap benefits to Firm A only. Which of the following statements about the swap is NOT correct?
A man just sold a call option to his counterparty, a lady. The man has just now:
A non-dividend paying stock has a current price of $20.
The risk free rate is 5% pa given as a continuously compounded rate.
A 2 year futures contract on the stock has a futures price of $24.
You suspect that the futures contract is mis-priced and would like to conduct a risk-free arbitrage that requires zero capital. Which of the following steps about arbitraging the situation is NOT correct?
Question 906 effective rate, return types, net discrete return, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its effective annual return be? Note that an effective annual return is also called a net discrete return per annum. If the price now is ##P_0## and the price in one year is ##P_1## then the effective annul return over the next year is:
###r_\text{effective annual} = \dfrac{P_1 - P_0}{P_0} = \text{NDR}_\text{annual}###Question 907 continuously compounding rate, return types, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its continuously compounded return ##(r_{CC})## be? If the price now is ##P_0## and the price in one year is ##P_1## then the continuously compounded return over the next year is:
###r_\text{CC annual} = \ln{\left[ \dfrac{P_1}{P_0} \right]} = \text{LGDR}_\text{annual}###Question 908 effective rate, return types, gross discrete return, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its gross discrete return (GDR) be? If the price now is ##P_0## and the price in one year is ##P_1## then the gross discrete return over the next year is:
###\text{GDR}_\text{annual} = \dfrac{P_1}{P_0}###If a variable, say X, is normally distributed with mean ##\mu## and variance ##\sigma^2## then mathematicians write ##X \sim \mathcal{N}(\mu, \sigma^2)##.
If a variable, say Y, is log-normally distributed and the underlying normal distribution has mean ##\mu## and variance ##\sigma^2## then mathematicians write ## Y \sim \mathbf{ln} \mathcal{N}(\mu, \sigma^2)##.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Select the most correct statement:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.

Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Which of the below statements is NOT correct?
Which of the following quantities is commonly assumed to be normally distributed?
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 720 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed.
In 5 years, what do you expect the median and mean prices to be? The answer options are given in the same order.
The symbol ##\text{GDR}_{0\rightarrow 1}## represents a stock's gross discrete return per annum over the first year. ##\text{GDR}_{0\rightarrow 1} = P_1/P_0##. The subscript indicates the time period that the return is mentioned over. So for example, ##\text{AAGDR}_{1 \rightarrow 3}## is the arithmetic average GDR measured over the two year period from years 1 to 3, but it is expressed as a per annum rate.
Which of the below statements about the arithmetic and geometric average GDR is NOT correct?
Question 723 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 99 | -0.010050 | 0.990000 | -0.010000 |
| 2 | 180.40 | 0.600057 | 1.822222 | 0.822222 |
| 3 | 112.73 | 0.470181 | 0.624889 | 0.375111 |
| Arithmetic average | 0.0399 | 1.1457 | 0.1457 | |
| Arithmetic standard deviation | 0.4384 | 0.5011 | 0.5011 | |
Question 722 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 50 | -0.6931 | 0.5 | -0.5 |
| 2 | 100 | 0.6931 | 2 | 1 |
| Arithmetic average | 0 | 1.25 | 0.25 | |
| Arithmetic standard deviation | 0.9802 | 1.0607 | 1.0607 | |
Question 792 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, log-normal distribution, confidence interval
A risk manager has identified that their investment fund’s continuously compounded portfolio returns are normally distributed with a mean of 10% pa and a standard deviation of 40% pa. The fund’s portfolio is currently valued at $1 million. Assume that there is no estimation error in the above figures. To simplify your calculations, all answers below use 2.33 as an approximation for the normal inverse cumulative density function at 99%. All answers are rounded to the nearest dollar. Assume one month is 1/12 of a year. Which of the following statements is NOT correct?
In the home loan market, the acronym LVR stands for Loan to Valuation Ratio. If you bought a house worth one million dollars, partly funded by an $800,000 home loan, then your LVR was 80%. The LVR is equivalent to which of the following ratios?
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
You deposit money into a bank. Which of the following statements is NOT correct? You:
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Delta buys a future from Alice.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?