Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
Question 22 NPV, perpetuity with growth, effective rate, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 10% given as an effective annual rate?
The first payment of $90 is in 3 years, followed by payments every 6 months in perpetuity after that which shrink by 3% every 6 months. That is, the growth rate every 6 months is actually negative 3%, given as an effective 6 month rate. So the payment at ## t=3.5 ## years will be ## 90(1-0.03)^1=87.3 ##, and so on.
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
Question 25 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 2 year zero coupon bond at a yield of 8% pa, and a
- 3 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
You really want to go on a back packing trip to Europe when you finish university. Currently you have $1,500 in the bank. Bank interest rates are 8% pa, given as an APR compounding per month. If the holiday will cost $2,000, how long will it take for your bank account to reach that amount?
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
A wholesale glass importer offers credit to its customers. Customers are given 30 days to pay for their goods, but if they pay within 5 days they will get a 1% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 5th day or the 30th day. All rates given below are effective annual rates.
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
The following is the Dividend Discount Model (DDM) used to price stocks:
### P_0 = \frac{d_1}{r-g} ###Assume that the assumptions of the DDM hold and that the time period is measured in years.
Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
A project to build a toll road will take 3 years to complete, costing three payments of $50 million, paid at the start of each year (at times 0, 1, and 2).
After completion, the toll road will yield a constant $10 million at the end of each year forever with no costs. So the first payment will be at t=4.
The required return of the project is 10% pa given as an effective nominal rate. All cash flows are nominal.
What is the payback period?
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Profitability Index (PI) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
The phone company Telstra have 2 mobile service plans on offer which both have the same amount of phone call, text message and internet data credit. Both plans have a contract length of 24 months and the monthly cost is payable in advance. The only difference between the two plans is that one is a:
- 'Bring Your Own' (BYO) mobile service plan, costing $50 per month. There is no phone included in this plan. The other plan is a:
- 'Bundled' mobile service plan that comes with the latest smart phone, costing $71 per month. This plan includes the latest smart phone.
Neither plan has any additional payments at the start or end.
The only difference between the plans is the phone, so what is the implied cost of the phone as a present value?
Assume that the discount rate is 2% per month given as an effective monthly rate, the same high interest rate on credit cards.
A wholesale horticulture nursery offers credit to its customers.
Customers are given 60 days to pay for their goods, but if they pay immediately they will get a 3% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay either immediately or on the 60th day. All rates given below are effective annual rates.
Question 48 IRR, NPV, bond pricing, premium par and discount bonds, market efficiency
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.
Using the dividend discount model, what will be the share price?
A three year project's NPV is negative. The cash flows of the project include a negative cash flow at the very start and positive cash flows over its short life. The required return of the project is 10% pa. Select the most correct statement.
A two year Government bond has a face value of $100, a yield of 2.5% pa and a fixed coupon rate of 0.5% pa, paid semi-annually. What is its price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in four and a half years (t = 4.5)?
Question 56 income and capital returns, bond pricing, premium par and discount bonds
Which of the following statements about risk free government bonds is NOT correct?
Hint: Total return can be broken into income and capital returns as follows:
###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###
The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
In Australia, domestic university students are allowed to buy concession tickets for the bus, train and ferry which sell at a discount of 50% to full-price tickets.
The Australian Government do not allow international university students to buy concession tickets, they have to pay the full price.
Some international students see this as unfair and they are willing to pay for fake university identification cards which have the concession sticker.
What is the most that an international student would be willing to pay for a fake identification card?
Assume that international students:
- consider buying their fake card on the morning of the first day of university from their neighbour, just before they leave to take the train into university.
- buy their weekly train tickets on the morning of the first day of each week.
- ride the train to university and back home again every day seven days per week until summer holidays 40 weeks from now. The concession card only lasts for those 40 weeks. Assume that there are 52 weeks in the year for the purpose of interest rate conversion.
- a single full-priced one-way train ride costs $5.
- have a discount rate of 11% pa, given as an effective annual rate.
Approach this question from a purely financial view point, ignoring the illegality, embarrassment and the morality of committing fraud.
A wholesale building supplies business offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.
What is the effective interest rate implicit in the discount being offered?
Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given below are effective annual rates.
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
Question 65 annuity with growth, needs refinement
Which of the below formulas gives the present value of an annuity with growth?
Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###
The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.
The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.
###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###
The equation of a perpetuity with growth is:
###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###Government bonds currently have a return of 5% pa. A stock has an expected return of 6% pa and the market return is 7% pa. What is the beta of the stock?
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Covariance ##(\sigma_{A,B})## | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the standard deviation (not variance) of the above portfolio? Note that the stocks' covariance is given, not correlation.
A firm's weighted average cost of capital before tax (##r_\text{WACC before tax}##) would increase due to:
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
Stock A and B's returns have a correlation of 0.3. Which statement is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the expected return of the above portfolio?
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
A company has:
- 140 million shares outstanding.
- The market price of one share is currently $2.
- The company's debentures are publicly traded and their market price is equal to 93% of the face value.
- The debentures have a total face value of $50,000,000 and the current yield to maturity of corporate debentures is 12% per annum.
- The risk-free rate is 8.50% and the market return is 13.7%.
- Market analysts estimated that the company's stock has a beta of 0.90.
- The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC) in a classical tax system?
Treasury bonds currently have a return of 5% pa. A stock has a beta of 0.5 and the market return is 10% pa. What is the expected return of the stock?
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of equity to raise money for new projects of similar systematic risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).
What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid annually. So there's only one coupon per year, paid in arrears every year.
Question 742 price gains and returns over time, no explanation
For an asset's price to quintuple (be five times as big, say from $1 to $5) every 5 years, what must be its effective annual capital return?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
A 10 year bond has a face value of $100, a yield of 6% pa and a fixed coupon rate of 8% pa, paid semi-annually. What is its price?
This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
A company has:
- 10 million common shares outstanding, each trading at a price of $90.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant dividend of 9% of par. They currently trade at a price of $120 each.
- Debentures that have a total face value of $60,000,000 and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 90% of their face value.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts estimate that the company's common stock has a beta of 1.2. The corporate tax rate is 30%.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
Question 905 market capitalisation of equity, PE ratio, payout ratio
The below graph shows the computer software company Microsoft's stock price (MSFT) at the market close on the NASDAQ on Friday 1 June 2018.
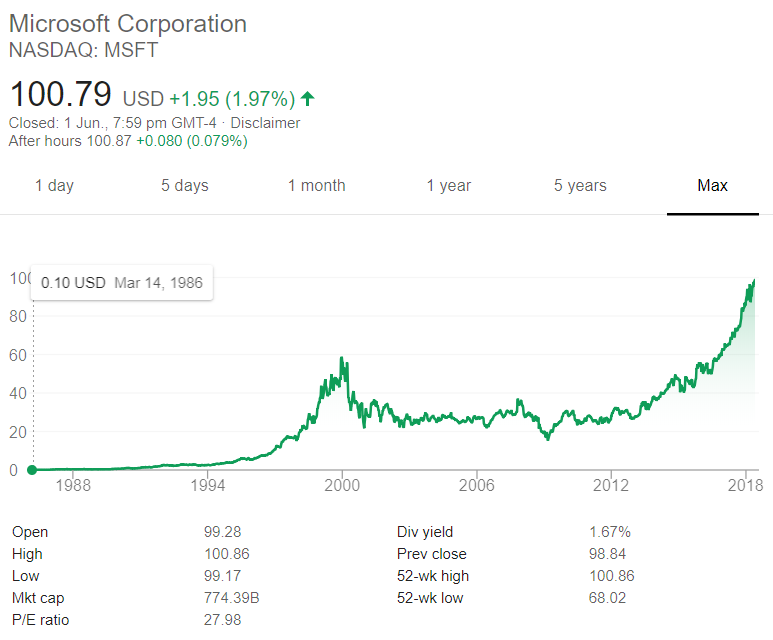
Based on the screenshot above, which of the following statements about MSFT is NOT correct? MSFT's:
What is the Cash Conversion Cycle for a firm with a:
- Payables period of 1 day;
- Inventory period of 50 days; and
- Receivables period of 30 days?
All answer options are in days:
A one year European-style call option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The call option price now is:
A one year European-style put option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The put option price now is:
A trader just bought a European style put option on CBA stock. The current option premium is $2, the exercise price is $75, the option matures in one year and the spot CBA stock price is $74.
Which of the following statements is NOT correct?
An equity index is currently at 4,800 points. The 1.5 year futures price is 5,100 points and the total required return is 6% pa with continuous compounding. Each index point is worth $25.
What is the implied dividend yield as a continuously compounded rate per annum?
A 2-year futures contract on a stock paying a continuous dividend yield of 3% pa was bought when the underlying stock price was $10 and the risk free rate was 10% per annum with continuous compounding. Assume that investors are risk-neutral, so the stock's total required return is the risk free rate.
Find the forward price ##(F_2)## and value of the contract ##(V_0)## initially. Also find the value of the contract in 6 months ##(V_{0.5})## if the stock price rose to $12.
A $100 stock has a continuously compounded expected total return of 10% pa. Its dividend yield is 2% pa with continuous compounding. What do you expect its price to be in one year?
A $100 stock has a continuously compounded expected total return of 10% pa. Its dividend yield is 2% pa with continuous compounding. What do you expect its price to be in 2.5 years?
An equity index is currently at 5,200 points. The 6 month futures price is 5,300 points and the total required return is 6% pa with continuous compounding. Each index point is worth $25.
What is the implied dividend yield as a continuously compounded rate per annum?
Question 691 continuously compounding rate, effective rate, continuously compounding rate conversion, no explanation
A bank quotes an interest rate of 6% pa with quarterly compounding. Note that another way of stating this rate is that it is an annual percentage rate (APR) compounding discretely every 3 months.
Which of the following statements about this rate is NOT correct? All percentages are given to 6 decimal places. The equivalent:
Question 707 continuously compounding rate, continuously compounding rate conversion
Convert a 10% effective annual rate ##(r_\text{eff annual})## into a continuously compounded annual rate ##(r_\text{cc annual})##. The equivalent continuously compounded annual rate is:
Question 708 continuously compounding rate, continuously compounding rate conversion
Convert a 10% continuously compounded annual rate ##(r_\text{cc annual})## into an effective annual rate ##(r_\text{eff annual})##. The equivalent effective annual rate is:
Which of the following interest rate quotes is NOT equivalent to a 10% effective annual rate of return? Assume that each year has 12 months, each month has 30 days, each day has 24 hours, each hour has 60 minutes and each minute has 60 seconds. APR stands for Annualised Percentage Rate.
Question 710 continuously compounding rate, continuously compounding rate conversion
A continuously compounded monthly return of 1% ##(r_\text{cc monthly})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
Question 711 continuously compounding rate, continuously compounding rate conversion
A continuously compounded semi-annual return of 5% ##(r_\text{cc 6mth})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
Question 584 option, option payoff at maturity, option profit
Which of the following statements about European call options on non-dividend paying stocks is NOT correct?
On 1 February 2016 you were told that your refinery company will need to purchase oil on 1 July 2016. You were afraid of the oil price rising between now and then so you bought some August 2016 futures contracts on 1 February 2016 to hedge against changes in the oil price. On 1 February 2016 the oil price was $40 and the August 2016 futures price was $43.
It's now 1 July 2016 and oil price is $45 and the August 2016 futures price is $46. You bought the spot oil and closed out your futures position on 1 July 2016.
What was the effective price paid for the oil, taking into account basis risk? All spot and futures oil prices quoted above and below are per barrel.
You intend to use futures on oil to hedge the risk of purchasing oil. There is no cross-hedging risk. Oil pays no dividends but it’s costly to store. Which of the following statements about basis risk in this scenario is NOT correct?
Which of the following statements about futures contracts on shares is NOT correct, assuming that markets are efficient?
When an equity future is first negotiated (at t=0):
After doing extensive fundamental analysis of a company, you believe that their shares are overpriced and will soon fall significantly. The market believes that there will be no such fall.
Which of the following strategies is NOT a good idea, assuming that your prediction is true?
A trader buys one December futures contract on orange juice. Each contract is for the delivery of 10,000 pounds. The current futures price is $1.20 per pound. The initial margin is $5,000 per contract, and the maintenance margin is $4,000 per contract.
What is the smallest price change would that would lead to a margin call for the buyer?
Which one of the below option and futures contracts gives the possibility of potentially unlimited gains?
Which of the below formulas gives the payoff at maturity ##(f_T)## from being long a future? Let the underlying asset price at maturity be ##S_T## and the locked-in futures price be ##K_T##.
Which of the below formulas gives the payoff at maturity ##(f_T)## from being short a future? Let the underlying asset price at maturity be ##S_T## and the locked-in futures price be ##K_T##.
A trader buys one crude oil futures contract on the CME expiring in one year with a locked-in futures price of $38.94 per barrel. If the trader doesn’t close out her contract before expiry then in one year she will have the:
A trader sells one crude oil futures contract on the CME expiring in one year with a locked-in futures price of $38.94 per barrel. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before expiry then in one year she will have the:
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Delta buys a future from Alice.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Delta buys a future from Bob.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
A trader buys a one year futures contract on crude oil. The contract is for the delivery of 1,000 barrels. The current futures price is $38.94 per barrel. The initial margin is $3,410 per contract, and the maintenance margin is $3,100 per contract.
What is the smallest price change that would lead to a margin call for the buyer?
A trader sells a one year futures contract on crude oil. The contract is for the delivery of 1,000 barrels. The current futures price is $38.94 per barrel. The initial margin is $3,410 per contract, and the maintenance margin is $3,100 per contract.
What is the smallest price change that would lead to a margin call for the seller?
Which of the following statements about futures and forward contracts is NOT correct?
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Bob buys a future from Chris.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Alice buys a future from Chris.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
An equity index stands at 100 points and the one year equity futures price is 102.
The equity index is expected to have a dividend yield of 4% pa. Assume that investors are risk-neutral so their total required return on the shares is the same as the risk free Treasury bond yield which is 10% pa. Both are given as discrete effective annual rates.
Assuming that the equity index is fairly priced, an arbitrageur would recognise that the equity futures are:
An equity index stands at 100 points and the one year equity futures price is 107.
The equity index is expected to have a dividend yield of 3% pa. Assume that investors are risk-neutral so their total required return on the shares is the same as the risk free Treasury bond yield which is 10% pa. Both are given as discrete effective annual rates.
Assuming that the equity index is fairly priced, an arbitrageur would recognise that the equity futures are:
Question 861 open interest, closing out future contract, no explanation
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys 2 future from Bob.
2. Chris buys 5 futures from Delta.
3. Chris buys 9 futures from Bob.
These were the only trades made in this equity index future.
Which of the following statements is NOT correct?
A pig farmer in the US is worried about the price of hogs falling and wants to lock in a price now. In one year the pig farmer intends to sell 1,000,000 pounds of hogs. Luckily, one year CME lean hog futures expire on the exact day that he wishes to sell his pigs. The futures have a notional principal of 40,000 pounds (about 18 metric tons) and currently trade at a price of 63.85 cents per pound. The underlying lean hogs spot price is 77.15 cents per pound. The correlation between the futures price and the underlying hogs price is one and the standard deviations are both 4 cents per pound. The initial margin is USD1,500 and the maintenance margin is USD1,200 per futures contract.
Which of the below statements is NOT correct?
The standard deviation of monthly changes in the spot price of corn is 50 cents per bushel. The standard deviation of monthly changes in the futures price of corn is 40 cents per bushel. The correlation between the spot price of corn and the futures price of corn is 0.9.
It is now March. A corn chip manufacturer is committed to buying 250,000 bushels of corn in May. The spot price of corn is 381 cents per bushel and the June futures price is 399 cents per bushel.
The corn chip manufacturer wants to use the June corn futures contracts to hedge his risk. Each futures contract is for the delivery of 5,000 bushels of corn. One bushel is about 127 metric tons.
How many corn futures should the corn chip manufacturer buy to hedge his risk? Round your answer to the nearest whole number of contracts. Remember to tail the hedge.
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys 2 futures from Bob.
2. Chris buys 3 futures from Delta.
3. Delta buys 5 futures from Alice.
Which of the following statements is NOT correct?
Which derivatives position has the possibility of unlimited potential gains?
Question 825 future, hedging, tailing the hedge, speculation, no explanation
An equity index fund manager controls a USD500 million diversified equity portfolio with a beta of 0.9. The equity manager expects a significant rally in equity prices next year. The market does not think that this will happen. If the fund manager wishes to increase his portfolio beta to 1.5, how many S&P500 futures should he buy?
The US market equity index is the S&P500. One year CME futures on the S&P500 currently trade at 2,155 points and the spot price is 2,180 points. Each point is worth $250.
The number of one year S&P500 futures contracts that the fund manager should buy is:
You bought a 1.5 year (18 month) futures contract on oil. Oil storage costs are 4% pa continuously compounded and oil pays no dividends. The futures contract is entered into when the oil price is $40 per barrel and the risk-free rate of interest is 10% per annum with continuous compounding.
Which of the following statements is NOT correct?
A stock is expected to pay its semi-annual dividend of $1 per share for the foreseeable future. The current stock price is $40 and the continuously compounded risk free rate is 3% pa for all maturities. An investor has just taken a long position in a 12-month futures contract on the stock. The last dividend payment was exactly 4 months ago. Therefore the next $1 dividend is in 2 months, and the $1 dividend after is 8 months from now. Which of the following statements about this scenario is NOT correct?
A non-dividend paying stock has a current price of $20.
The risk free rate is 5% pa given as a continuously compounded rate.
A 2 year futures contract on the stock has a futures price of $24.
You suspect that the futures contract is mis-priced and would like to conduct a risk-free arbitrage that requires zero capital. Which of the following steps about arbitraging the situation is NOT correct?
A non-dividend paying stock has a current price of $20.
The risk free rate is 5% pa given as a continuously compounded rate.
Options on the stock are currently priced at $5 for calls and $5.55 for puts where both options have a 2 year maturity and an exercise price of $24.
You suspect that the call option contract is mis-priced and would like to conduct a risk-free arbitrage that requires zero capital. Which of the following steps about arbitraging the situation is NOT correct?
Which of the following terms about options are NOT synonyms?
Question 821 option, option profit, option payoff at maturity, no explanation
You just paid $4 for a 3 month European style call option on a stock currently priced at $47 with a strike price of $50. The stock’s next dividend will be $1 in 4 months’ time. Note that the dividend is paid after the option matures. Which of the below statements is NOT correct?
When does a European option's last-traded market price become a sunk cost?
Question 823 option, option payoff at maturity, option profit, no explanation
A European call option should only be exercised if:
Below are some statements about European-style options on non-dividend paying stocks. Assume that the risk free rate is always positive. Which of these statements is NOT correct?
Question 831 option, American option, no explanation
Which of the following statements about American-style options is NOT correct? American-style:
A 12 month European-style call option with a strike price of $11 is written on a dividend paying stock currently trading at $10. The dividend is paid annually and the next dividend is expected to be $0.40, paid in 9 months. The risk-free interest rate is 5% pa continuously compounded and the standard deviation of the stock’s continuously compounded returns is 30 percentage points pa. The stock's continuously compounded returns are normally distributed. Using the Black-Scholes-Merton option valuation model, determine which of the following statements is NOT correct.
A company has a 95% daily Value at Risk (VaR) of $1 million. The units of this VaR are in:
Question 790 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, log-normal distribution, VaR, confidence interval
A risk manager has identified that their hedge fund’s continuously compounded portfolio returns are normally distributed with a mean of 10% pa and a standard deviation of 30% pa. The hedge fund’s portfolio is currently valued at $100 million. Assume that there is no estimation error in these figures and that the normal cumulative density function at 1.644853627 is 95%.
Which of the following statements is NOT correct? All answers are rounded to the nearest dollar.
Question 792 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, log-normal distribution, confidence interval
A risk manager has identified that their investment fund’s continuously compounded portfolio returns are normally distributed with a mean of 10% pa and a standard deviation of 40% pa. The fund’s portfolio is currently valued at $1 million. Assume that there is no estimation error in the above figures. To simplify your calculations, all answers below use 2.33 as an approximation for the normal inverse cumulative density function at 99%. All answers are rounded to the nearest dollar. Assume one month is 1/12 of a year. Which of the following statements is NOT correct?
Question 785 fixed for floating interest rate swap, non-intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 3 | L - 0.4 | ||
| Firm B | 5 | L + 1 | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design a non-intermediated swap that benefits firm A only. What will be the swap rate?
A company can invest funds in a five year project at LIBOR plus 50 basis points pa. The five-year swap rate is 4% pa. What fixed rate of interest can the company earn over the next five years by using the swap?
Question 786 fixed for floating interest rate swap, intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 3 | L - 0.4 | ||
| Firm B | 5 | L + 1 | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design an intermediated swap (which means there will actually be two swaps) that nets a bank 0.1% and shares the remaining swap benefits between Firms A and B equally. Which of the following statements about the swap is NOT correct?
Question 787 fixed for floating interest rate swap, intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 2 | L - 0.1 | ||
| Firm B | 2.5 | L | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design an intermediated swap (which means there will actually be two swaps) that nets a bank 0.15% and grants the remaining swap benefits to Firm A only. Which of the following statements about the swap is NOT correct?
Question 956 option, Black-Scholes-Merton option pricing, delta hedging, hedging
A bank sells a European call option on a non-dividend paying stock and delta hedges on a daily basis. Below is the result of their hedging, with columns representing consecutive days. Assume that there are 365 days per year and interest is paid daily in arrears.
| Delta Hedging a Short Call using Stocks and Debt | |||||||
| Description | Symbol | Days to maturity (T in days) | |||||
| 60 | 59 | 58 | 57 | 56 | 55 | ||
| Spot price ($) | S | 10000 | 10125 | 9800 | 9675 | 10000 | 10000 |
| Strike price ($) | K | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 |
| Risk free cont. comp. rate (pa) | r | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | σ | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| Option maturity (years) | T | 0.164384 | 0.161644 | 0.158904 | 0.156164 | 0.153425 | 0.150685 |
| Delta | N[d1] = dc/dS | 0.552416 | 0.582351 | 0.501138 | 0.467885 | 0.550649 | 0.550197 |
| Probability that S > K at maturity in risk neutral world | N[d2] | 0.487871 | 0.51878 | 0.437781 | 0.405685 | 0.488282 | 0.488387 |
| Call option price ($) | c | 685.391158 | 750.26411 | 567.990995 | 501.487157 | 660.982878 | ? |
| Stock investment value ($) | N[d1]*S | 5524.164129 | 5896.301781 | 4911.152036 | 4526.788065 | 5506.488143 | ? |
| Borrowing which partly funds stock investment ($) | N[d2]*K/e^(r*T) | 4838.772971 | 5146.037671 | 4343.161041 | 4025.300909 | 4845.505265 | ? |
| Interest expense from borrowing paid in arrears ($) | r*N[d2]*K/e^(r*T) | 0.662891 | 0.704985 | 0.594994 | 0.551449 | ? | |
| Gain on stock ($) | N[d1]*(SNew - SOld) | 69.052052 | -189.264008 | -62.642245 | 152.062648 | ? | |
| Gain on short call option ($) | -1*(cNew - cOld) | -64.872952 | 182.273114 | 66.503839 | -159.495721 | ? | |
| Net gain ($) | Gains - InterestExpense | 3.516209 | -7.695878 | 3.266599 | -7.984522 | ? | |
| Gamma | Γ = d^2c/dS^2 | 0.000244 | 0.00024 | 0.000255 | 0.00026 | 0.000253 | 0.000255 |
| Theta | θ = dc/dT | 2196.873429 | 2227.881353 | 2182.174706 | 2151.539751 | 2266.589184 | 2285.1895 |
In the last column when there are 55 days left to maturity there are missing values. Which of the following statements about those missing values is NOT correct?
Question 948 VaR, expected shortfall
Below is a historical sample of returns on the S&P500 capital index.
| S&P500 Capital Index Daily Returns Ranked from Best to Worst |
||
| 10,000 trading days from 4th August 1977 to 24 March 2017 based on closing prices. |
||
| Rank | Date (DD-MM-YY) |
Continuously compounded daily return (% per day) |
| 1 | 21-10-87 | 9.23 |
| 2 | 08-03-83 | 8.97 |
| 3 | 13-11-08 | 8.3 |
| 4 | 30-09-08 | 8.09 |
| 5 | 28-10-08 | 8.01 |
| 6 | 29-10-87 | 7.28 |
| … | … | … |
| 9980 | 11-12-08 | -5.51 |
| 9981 | 22-10-08 | -5.51 |
| 9982 | 08-08-11 | -5.54 |
| 9983 | 22-09-08 | -5.64 |
| 9984 | 11-09-86 | -5.69 |
| 9985 | 30-11-87 | -5.88 |
| 9986 | 14-04-00 | -5.99 |
| 9987 | 07-10-98 | -6.06 |
| 9988 | 08-01-88 | -6.51 |
| 9989 | 27-10-97 | -6.55 |
| 9990 | 13-10-89 | -6.62 |
| 9991 | 15-10-08 | -6.71 |
| 9992 | 29-09-08 | -6.85 |
| 9993 | 07-10-08 | -6.91 |
| 9994 | 14-11-08 | -7.64 |
| 9995 | 01-12-08 | -7.79 |
| 9996 | 29-10-08 | -8.05 |
| 9997 | 26-10-87 | -8.4 |
| 9998 | 31-08-98 | -8.45 |
| 9999 | 09-10-08 | -12.9 |
| 10000 | 19-10-87 | -23.36 |
| Mean of all 10,000: | 0.0354 | |
| Sample standard deviation of all 10,000: | 1.2062 | |
| Sources: Bloomberg and S&P. | ||
Assume that the one-tail Z-statistic corresponding to a probability of 99.9% is exactly 3.09. Which of the following statements is NOT correct? Based on the historical data, the 99.9% daily:
Question 791 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, log-normal distribution, VaR, confidence interval
A risk manager has identified that their pension fund’s continuously compounded portfolio returns are normally distributed with a mean of 5% pa and a standard deviation of 20% pa. The fund’s portfolio is currently valued at $1 million. Assume that there is no estimation error in the above figures. To simplify your calculations, all answers below use 2.33 as an approximation for the normal inverse cumulative density function at 99%. All answers are rounded to the nearest dollar. Which of the following statements is NOT correct?
Question 906 effective rate, return types, net discrete return, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its effective annual return be? Note that an effective annual return is also called a net discrete return per annum. If the price now is ##P_0## and the price in one year is ##P_1## then the effective annul return over the next year is:
###r_\text{effective annual} = \dfrac{P_1 - P_0}{P_0} = \text{NDR}_\text{annual}###Question 907 continuously compounding rate, return types, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its continuously compounded return ##(r_{CC})## be? If the price now is ##P_0## and the price in one year is ##P_1## then the continuously compounded return over the next year is:
###r_\text{CC annual} = \ln{\left[ \dfrac{P_1}{P_0} \right]} = \text{LGDR}_\text{annual}###Question 908 effective rate, return types, gross discrete return, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its gross discrete return (GDR) be? If the price now is ##P_0## and the price in one year is ##P_1## then the gross discrete return over the next year is:
###\text{GDR}_\text{annual} = \dfrac{P_1}{P_0}###If a variable, say X, is normally distributed with mean ##\mu## and variance ##\sigma^2## then mathematicians write ##X \sim \mathcal{N}(\mu, \sigma^2)##.
If a variable, say Y, is log-normally distributed and the underlying normal distribution has mean ##\mu## and variance ##\sigma^2## then mathematicians write ## Y \sim \mathbf{ln} \mathcal{N}(\mu, \sigma^2)##.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.
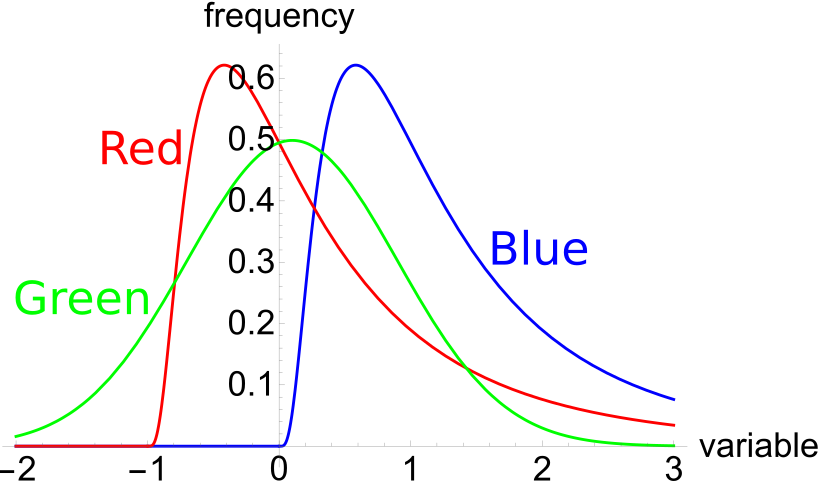
Select the most correct statement:
Question 925 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, no explanation
The arithmetic average and standard deviation of returns on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 were calculated as follows:
###\bar{r}_\text{yearly} = \dfrac{ \displaystyle\sum\limits_{t=1992}^{24}{\left( \ln \left( \dfrac{P_{t+1}}{P_t} \right) \right)} }{T} = \text{AALGDR} =0.0949=9.49\% \text{ pa}###
###\sigma_\text{yearly} = \dfrac{ \displaystyle\sum\limits_{t=1992}^{24}{\left( \left( \ln \left( \dfrac{P_{t+1}}{P_t} \right) - \bar{r}_\text{yearly} \right)^2 \right)} }{T} = \text{SDLGDR} = 0.1692=16.92\text{ pp pa}###
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
Which of the following statements is NOT correct? If you invested $1m today in the ASX200, then over the next 4 years:
Question 793 option, hedging, delta hedging, gamma hedging, gamma, Black-Scholes-Merton option pricing
A bank buys 1000 European put options on a $10 non-dividend paying stock at a strike of $12. The bank wishes to hedge this exposure. The bank can trade the underlying stocks and European call options with a strike price of 7 on the same stock with the same maturity. Details of the call and put options are given in the table below. Each call and put option is on a single stock.
| European Options on a Non-dividend Paying Stock | |||
| Description | Symbol | Put Values | Call Values |
| Spot price ($) | ##S_0## | 10 | 10 |
| Strike price ($) | ##K_T## | 12 | 7 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.4 | 0.4 |
| Option maturity (years) | ##T## | 1 | 1 |
| Option price ($) | ##p_0## or ##c_0## | 2.495350486 | 3.601466138 |
| ##N[d_1]## | ##\partial c/\partial S## | 0.888138405 | |
| ##N[d_2]## | ##N[d_2]## | 0.792946442 | |
| ##-N[-d_1]## | ##\partial p/\partial S## | -0.552034778 | |
| ##N[-d_2]## | ##N[-d_2]## | 0.207053558 | |
| Gamma | ##\Gamma = \partial^2 c/\partial S^2## or ##\partial^2 p/\partial S^2## | 0.098885989 | 0.047577422 |
| Theta | ##\Theta = \partial c/\partial T## or ##\partial p/\partial T## | 0.348152078 | 0.672379961 |
Which of the following statements is NOT correct?
Question 720 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed.
In 5 years, what do you expect the median and mean prices to be? The answer options are given in the same order.
Which of the following quantities is commonly assumed to be normally distributed?
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Which of the below statements is NOT correct?
Question 926 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the median dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Question 927 mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the mean dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
A one year European-style call option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
A one year European-style put option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The put option price now is:
The DuPont formula is:
###\dfrac{\text{Net Profit}}{\text{Sales}} \times \dfrac{\text{Sales}}{\text{Total Assets}} \times \dfrac{\text{Total Assets}}{\text{Owners' Equity}}###
Which of the following statements about the DuPont formula is NOT correct?
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Which of the following companies is most suitable for valuation using PE multiples techniques?
Which of the following investable assets is the LEAST suitable for valuation using PE multiples techniques?
A mature firm has constant expected future earnings and dividends. Both amounts are equal. So earnings and dividends are expected to be equal and unchanging.
Which of the following statements is NOT correct?
Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.
A firm has 1 million shares which trade at a price of $30 each. The firm is expected to announce earnings of $3 million at the end of the year and pay an annual dividend of $1.50 per share.
What is the firm's (forward looking) price/earnings (PE) ratio?
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.
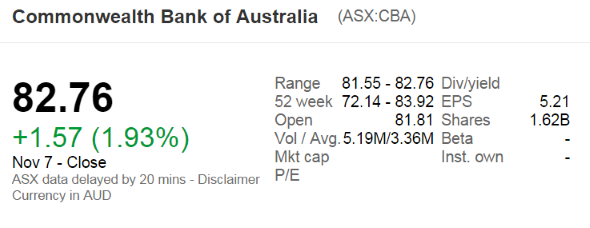
What was CBA's backwards-looking price-earnings ratio?
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.
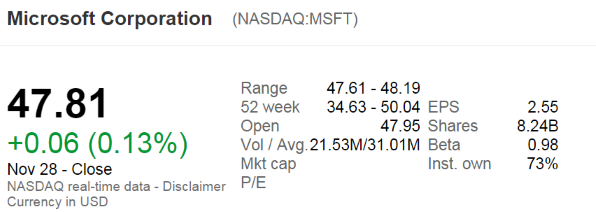
What was MSFT's backwards-looking price-earnings ratio?
A firm has 2m shares and a market capitalisation of equity of $30m. The firm just announced earnings of $5m and paid an annual dividend of $0.75 per share.
What is the firm's (backward looking) price/earnings (PE) ratio?
Estimate the French bank Societe Generale's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that EUR is the euro, the European monetary union's currency.
- The 4 major European banks Credit Agricole (ACA), Deutsche Bank AG (DBK), UniCredit (UCG) and Banco Santander (SAN) are comparable companies to Societe Generale (GLE);
- Societe Generale's (GLE's) historical earnings per share (EPS) is EUR 2.92;
- ACA's backward-looking PE ratio is 16.29 and historical EPS is EUR 0.84;
- DBK's backward-looking PE ratio is 25.01 and historical EPS is EUR 1.26;
- SAN's backward-looking PE ratio is 14.71 and historical EPS is EUR 0.47;
- UCG's backward-looking PE ratio is 15.78 and historical EPS is EUR 0.40;
Note: Figures sourced from Google Finance on 27 March 2015.
Question 547 PE ratio, Multiples valuation, DDM, income and capital returns, no explanation
A firm pays out all of its earnings as dividends. Because of this, the firm has no real growth in earnings, dividends or stock price since there is no re-investment back into the firm to buy new assets and make higher earnings. The dividend discount model is suitable to value this company.
The firm's revenues and costs are expected to increase by inflation in the foreseeable future. The firm has no debt. It operates in the services industry and has few physical assets so there is negligible depreciation expense and negligible net working capital required.
Which of the following statements about this firm's PE ratio is NOT correct? The PE ratio should:
Note: The inverse of x is 1/x.
Itau Unibanco is a major listed bank in Brazil with a market capitalisation of equity equal to BRL 85.744 billion, EPS of BRL 3.96 and 2.97 billion shares on issue.
Banco Bradesco is another major bank with total earnings of BRL 8.77 billion and 2.52 billion shares on issue.
Estimate Banco Bradesco's current share price using a price-earnings multiples approach assuming that Itau Unibanco is a comparable firm.
Note that BRL is the Brazilian Real, their currency. Figures sourced from Google Finance on the market close of the BVMF on 24 July 2015.
The below diagram shows a firm’s cash cycle.
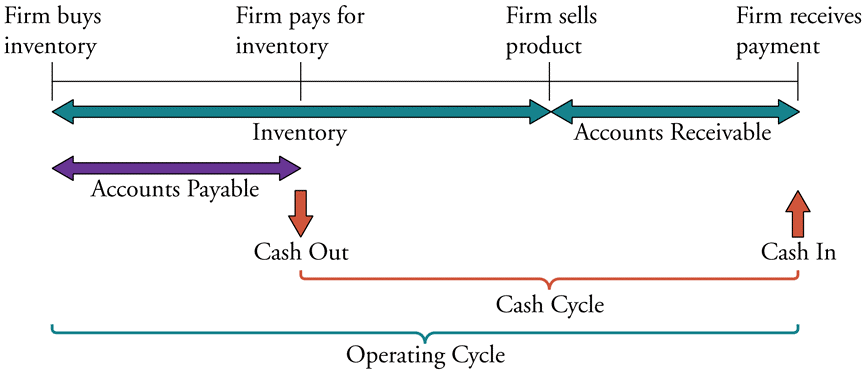
Which of the following statements about companies’ cash cycle is NOT correct?
Question 472 quick ratio, accounting ratio
A firm has current assets totaling $1.5b of which cash is $0.25b and inventories is $0.5b. Current liabilities total $2b of which accounts payable is $1b.
What is the firm's quick ratio, also known as the acid test ratio?
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
High risk firms in danger of bankruptcy tend to have:
A firm has a debt-to-equity ratio of 25%. What is its debt-to-assets ratio?
A firm has a debt-to-equity ratio of 60%. What is its debt-to-assets ratio?
A firm has a debt-to-assets ratio of 20%. What is its debt-to-equity ratio?
In the home loan market, the acronym LVR stands for Loan to Valuation Ratio. If you bought a house worth one million dollars, partly funded by an $800,000 home loan, then your LVR was 80%. The LVR is equivalent to which of the following ratios?
Safe firms with low chances of bankruptcy will tend to have:
A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Question 419 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM, no explanation
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $6m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 9m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $6 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense in first year (at t=1) | $0.53m | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.08 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-assets ratio | 50% | |
Notes
- Due to the project, current assets will increase by $5m now (t=0) and fall by $5m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-assets ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| UniBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 80 | |
| COGS | 40 | |
| Operating expense | 15 | |
| Depreciation | 10 | |
| Interest expense | 5 | |
| Income before tax | 10 | |
| Tax at 30% | 3 | |
| Net income | 7 | |
| UniBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 90 |
| PPE | ||
| Cost | 360 | 320 |
| Accumul. depr. | 40 | 30 |
| Carrying amount | 320 | 290 |
| Total assets | 440 | 380 |
| Liabilities | ||
| Current liabilities | 110 | 60 |
| Non-current liabilities | 190 | 180 |
| Owners' equity | ||
| Retained earnings | 95 | 95 |
| Contributed equity | 45 | 45 |
| Total L and OE | 440 | 380 |
Note: all figures are given in millions of dollars ($m).
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| World Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 300 | |
| COGS | 150 | |
| Operating expense | 50 | |
| Depreciation | 40 | |
| Interest expense | 10 | |
| Taxable income | 50 | |
| Tax at 30% | 15 | |
| Net income | 35 | |
| World Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 200 | 230 |
| PPE | ||
| Cost | 400 | 400 |
| Accumul. depr. | 75 | 35 |
| Carrying amount | 325 | 365 |
| Total assets | 525 | 595 |
| Liabilities | ||
| Current liabilities | 150 | 205 |
| Non-current liabilities | 235 | 250 |
| Owners' equity | ||
| Retained earnings | 100 | 100 |
| Contributed equity | 40 | 40 |
| Total L and OE | 525 | 595 |
Note: all figures above and below are given in millions of dollars ($m).
Value the following business project to manufacture a new product.
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $3m | |
| Expected sale price of equipment at end of project | $0.6m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense per year | 0 | |
| Tax rate | 30% | |
| Weighted average cost of capital after tax per annum | 10% | |
Notes
- The firm's current assets and current liabilities are $3m and $2m respectively right now. This net working capital will not be used in this project, it will be used in other unrelated projects.
Due to the project, current assets (mostly inventory) will grow by $2m initially (at t = 0), and then by $0.2m at the end of the first year (t=1).
Current liabilities (mostly trade creditors) will increase by $0.1m at the end of the first year (t=1).
At the end of the project, the net working capital accumulated due to the project can be sold for the same price that it was bought. - The project cost $0.5m to research which was incurred one year ago.
Assumptions
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 3% pa.
- All rates are given as effective annual rates.
- The business considering the project is run as a 'sole tradership' (run by an individual without a company) and is therefore eligible for a 50% capital gains tax discount when the equipment is sold, as permitted by the Australian Tax Office.
What is the expected net present value (NPV) of the project?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###There are many different ways to value a firm's assets. Which of the following will NOT give the correct market value of a levered firm's assets ##(V_L)##? Assume that:
- The firm is financed by listed common stock and vanilla annual fixed coupon bonds, which are both traded in a liquid market.
- The bonds' yield is equal to the coupon rate, so the bonds are issued at par. The yield curve is flat and yields are not expected to change. When bonds mature they will be rolled over by issuing the same number of new bonds with the same expected yield and coupon rate, and so on forever.
- Tax rates on the dividends and capital gains received by investors are equal, and capital gains tax is paid every year, even on unrealised gains regardless of when the asset is sold.
- There is no re-investment of the firm's cash back into the business. All of the firm's excess cash flow is paid out as dividends so real growth is zero.
- The firm operates in a mature industry with zero real growth.
- All cash flows and rates in the below equations are real (not nominal) and are expected to be stable forever. Therefore the perpetuity equation with no growth is suitable for valuation.
Where:
###r_\text{WACC before tax} = r_D.\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital before tax}### ###r_\text{WACC after tax} = r_D.(1-t_c).\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital after tax}### ###NI_L=(Rev-COGS-FC-Depr-\mathbf{IntExp}).(1-t_c) = \text{Net Income Levered}### ###CFFA_L=NI_L+Depr-CapEx - \varDelta NWC+\mathbf{IntExp} = \text{Cash Flow From Assets Levered}### ###NI_U=(Rev-COGS-FC-Depr).(1-t_c) = \text{Net Income Unlevered}### ###CFFA_U=NI_U+Depr-CapEx - \varDelta NWC= \text{Cash Flow From Assets Unlevered}###A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
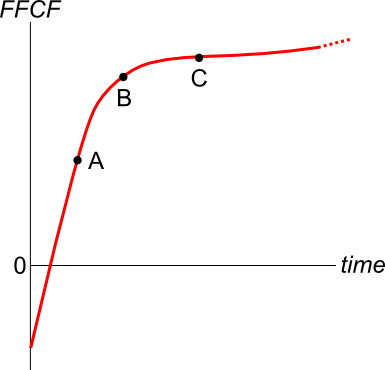
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
An old company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
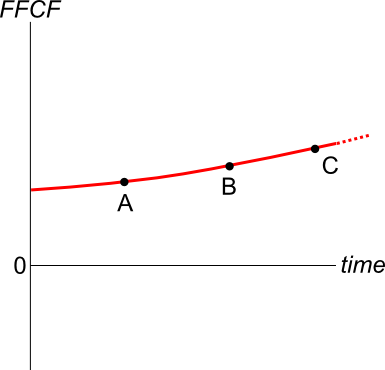
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
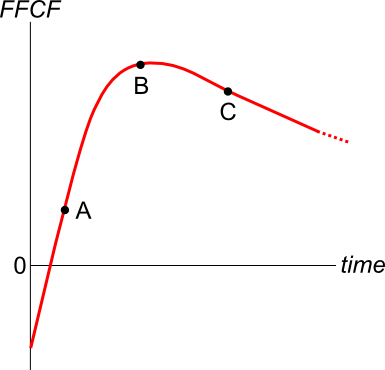
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Achieve firm free cash flow (FFCF or CFFA) of $1m.
- Pay dividends of $1.8m
- Complete a $1.3m share buy-back.
- Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Find Ching-A-Lings Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Ching-A-Lings Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 20 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 30 | |
| Taxes at 30% | 9 | |
| Net income | 21 | |
| Ching-A-Lings Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 49 | 38 |
| Trade debtors | 14 | 2 |
| Rent paid in advance | 5 | 5 |
| PPE | 400 | 400 |
| Total assets | 468 | 445 |
| Trade creditors | 4 | 10 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 145 | 145 |
| Retained profits | 119 | 100 |
| Total L and OE | 468 | 445 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
- Pay dividends of $1m.
- Complete a $1.3m share buy-back.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.
Which of the below FFCF formulas include the interest tax shield in the cash flow?
###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use earnings before interest and tax (EBIT).
###\begin{aligned} FFCF &= (EBIT)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ \end{aligned} \\###
Question 370 capital budgeting, NPV, interest tax shield, WACC, CFFA
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $600k | |
| Depreciation of equipment per year | $250k | |
| Expected sale price of equipment at end of project | $200k | |
| Revenue per job | $12k | |
| Variable cost per job | $4k | |
| Quantity of jobs per year | 120 | |
| Fixed costs per year, paid at the end of each year | $100k | |
| Interest expense in first year (at t=1) | $16.091k | |
| Interest expense in second year (at t=2) | $9.711k | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Levered cost of equity | 12.5% | |
| Market portfolio return | 10% | |
| Beta of assets | 1.24 | |
| Beta of levered equity | 1.5 | |
| Firm's and project's debt-to-equity ratio | 25% | |
Notes
- The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
- Thousands are represented by 'k' (kilo).
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are nominal. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use net operating profit after tax (NOPAT).
###\begin{aligned} FFCF &= NOPAT + Depr - CapEx -\Delta NWC \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC \\ \end{aligned} \\###
The hardest and most important aspect of business project valuation is the estimation of the:
Question 413 CFFA, interest tax shield, depreciation tax shield
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA).
One method is to use the following formulas to transform net income (NI) into FFCF including interest and depreciation tax shields:
###FFCF=NI + Depr - CapEx -ΔNWC + IntExp###
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )###
Another popular method is to use EBITDA rather than net income. EBITDA is defined as:
###EBITDA=Rev - COGS - FC###
One of the below formulas correctly calculates FFCF from EBITDA, including interest and depreciation tax shields, giving an identical answer to that above. Which formula is correct?
Question 418 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $8m | |
| Depreciation of equipment per year | $8m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 4m | |
| Sale price per unit | $10 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense in first year (at t=1) | $0.562m | |
| Corporate tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 9% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.32 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-equity ratio | 50% | |
Notes
- Due to the project, current assets will increase by $6m now (t=0) and fall by $6m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa. All rates are given as effective annual rates.
- The project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Question 658 CFFA, income statement, balance sheet, no explanation
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the income statement needed? Note that the income statement is sometimes also called the profit and loss, P&L, or statement of financial performance.
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the balance sheet needed? Note that the balance sheet is sometimes also called the statement of financial position.
Find the cash flow from assets (CFFA) of the following project.
| Project Data | |
| Project life | 2 years |
| Initial investment in equipment | $8m |
| Depreciation of equipment per year for tax purposes | $3m |
| Unit sales per year | 10m |
| Sale price per unit | $9 |
| Variable cost per unit | $4 |
| Fixed costs per year, paid at the end of each year | $2m |
| Tax rate | 30% |
Note 1: Due to the project, the firm will have to purchase $40m of inventory initially (at t=0). Half of this inventory will be sold at t=1 and the other half at t=2.
Note 2: The equipment will have a book value of $2m at the end of the project for tax purposes. However, the equipment is expected to fetch $1m when it is sold. Assume that the full capital loss is tax-deductible and taxed at the full corporate tax rate.
Note 3: The project will be fully funded by equity which investors will expect to pay dividends totaling $10m at the end of each year.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
Find the cash flow from assets (CFFA) of the following project.
| Project Data | ||
| Project life | 2 years | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year for tax purposes | $1m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $3 | |
| Fixed costs per year, paid at the end of each year | $1.5m | |
| Tax rate | 30% | |
Note 1: The equipment will have a book value of $4m at the end of the project for tax purposes. However, the equipment is expected to fetch $0.9 million when it is sold at t=2.
Note 2: Due to the project, the firm will have to purchase $0.8m of inventory initially, which it will sell at t=1. The firm will buy another $0.8m at t=1 and sell it all again at t=2 with zero inventory left. The project will have no effect on the firm's current liabilities.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
Find the cash flow from assets (CFFA) of the following project.
| One Year Mining Project Data | ||
| Project life | 1 year | |
| Initial investment in building mine and equipment | $9m | |
| Depreciation of mine and equipment over the year | $8m | |
| Kilograms of gold mined at end of year | 1,000 | |
| Sale price per kilogram | $0.05m | |
| Variable cost per kilogram | $0.03m | |
| Before-tax cost of closing mine at end of year | $4m | |
| Tax rate | 30% | |
Note 1: Due to the project, the firm also anticipates finding some rare diamonds which will give before-tax revenues of $1m at the end of the year.
Note 2: The land that will be mined actually has thermal springs and a family of koalas that could be sold to an eco-tourist resort for an after-tax amount of $3m right now. However, if the mine goes ahead then this natural beauty will be destroyed.
Note 3: The mining equipment will have a book value of $1m at the end of the year for tax purposes. However, the equipment is expected to fetch $2.5m when it is sold.
Find the project's CFFA at time zero and one. Answers are given in millions of dollars ($m), with the first cash flow at time zero, and the second at time one.
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?
You may assume:
- the value of debt (D) is constant through time,
- The cost of debt and the yield on debt are equal and given by ##r_D##.
- the appropriate rate to discount interest tax shields is ##r_D##.
- ##\text{IntExp}=D.r_D##
Question 237 WACC, Miller and Modigliani, interest tax shield
Which of the following discount rates should be the highest for a levered company? Ignore the costs of financial distress.
Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.
For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.
The advantage of negative gearing is an example of the benefits of:
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
Question 771 debt terminology, interest expense, interest tax shield, credit risk, no explanation
You deposit money into a bank account. Which of the following statements about this deposit is NOT correct?
Question 772 interest tax shield, capital structure, leverage
A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?
Question 941 negative gearing, leverage, capital structure, interest tax shield, real estate
Last year, two friends Lev and Nolev each bought similar investment properties for $1 million. Both earned net rents of $30,000 pa over the past year. They funded their purchases in different ways:
- Lev used $200,000 of his own money and borrowed $800,000 from the bank in the form of an interest-only loan with an interest rate of 5% pa.
- Nolev used $1,000,000 of his own money, he has no mortgage loan on his property.
Both Lev and Nolev also work in high-paying jobs and are subject personal marginal tax rates of 45%.
Which of the below statements about the past year is NOT correct?
You believe that the price of a share will fall significantly very soon, but the rest of the market does not. The market thinks that the share price will remain the same. Assuming that your prediction will soon be true, which of the following trades is a bad idea? In other words, which trade will NOT make money or prevent losses?
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
Question 987 interest tax shield, capital structure, debt terminology
What creates interest tax shields for a company?
Question 657 systematic and idiosyncratic risk, CAPM, no explanation
A stock's required total return will decrease when its:
Question 576 inflation, real and nominal returns and cash flows
What is the present value of a nominal payment of $1,000 in 4 years? The nominal discount rate is 8% pa and the inflation rate is 2% pa.
Question 577 inflation, real and nominal returns and cash flows
What is the present value of a real payment of $500 in 2 years? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Question 604 inflation, real and nominal returns and cash flows
Apples and oranges currently cost $1 each. Inflation is 5% pa, and apples and oranges are equally affected by this inflation rate. Note that when payments are not specified as real, as in this question, they're conventionally assumed to be nominal.
Which of the following statements is NOT correct?
Question 664 real and nominal returns and cash flows, inflation, no explanation
What is the present value of real payments of $100 every year forever, with the first payment in one year? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Question 727 inflation, real and nominal returns and cash flows
The Australian Federal Government lends money to domestic students to pay for their university education. This is known as the Higher Education Contribution Scheme (HECS). The nominal interest rate on the HECS loan is set equal to the consumer price index (CPI) inflation rate. The interest is capitalised every year, which means that the interest is added to the principal. The interest and principal does not need to be repaid by students until they finish study and begin working.
Which of the following statements about HECS loans is NOT correct?
Question 732 real and nominal returns and cash flows, inflation, income and capital returns
An investor bought a bond for $100 (at t=0) and one year later it paid its annual coupon of $1 (at t=1). Just after the coupon was paid, the bond price was $100.50 (at t=1). Inflation over the past year (from t=0 to t=1) was 3% pa, given as an effective annual rate.
Which of the following statements is NOT correct? The bond investment produced a:
Question 734 real and nominal returns and cash flows, inflation, DDM, no explanation
An equities analyst is using the dividend discount model to price a company's shares. The company operates domestically and has no plans to expand overseas. It is part of a mature industry with stable positive growth prospects.
The analyst has estimated the real required return (r) of the stock and the value of the dividend that the stock just paid a moment before ##(C_\text{0 before})##.
What is the highest perpetual real growth rate of dividends (g) that can be justified? Select the most correct statement from the following choices. The highest perpetual real expected growth rate of dividends that can be justified is the country's expected:
Question 739 real and nominal returns and cash flows, inflation
There are a number of different formulas involving real and nominal returns and cash flows. Which one of the following formulas is NOT correct? All returns are effective annual rates. Note that the symbol ##\approx## means 'approximately equal to'.
Question 744 income and capital returns, real and nominal returns and cash flows, inflation
If someone says "my shares rose by 10% last year", what do you assume that they mean? The effective annual:
Question 745 real and nominal returns and cash flows, inflation, income and capital returns
If the nominal gold price is expected to increase at the same rate as inflation which is 3% pa, which of the following statements is NOT correct?
Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
You work for XYZ company and you’ve been asked to evaluate a new project which has double the systematic risk of the company’s other projects.
You use the Capital Asset Pricing Model (CAPM) formula and input the treasury yield ##(r_f )##, market risk premium ##(r_m-r_f )## and the company’s asset beta risk factor ##(\beta_{XYZ} )## into the CAPM formula which outputs a return.
This return that you’ve just found is:
Government bonds currently have a return of 5%. A stock has a beta of 2 and the market return is 7%. What is the expected return of the stock?
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
Question 104 CAPM, payout policy, capital structure, Miller and Modigliani, risk
Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.
For a firm operating in this perfect world, which statement(s) are correct?
(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.
(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.
(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.
Select the most correct response:
A fairly priced stock has an expected return of 15% pa. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the beta of the stock?
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
A fairly priced stock has a beta that is the same as the market portfolio's beta. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the expected return of the stock?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the price of the stock now?
Question 244 CAPM, SML, NPV, risk
Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:
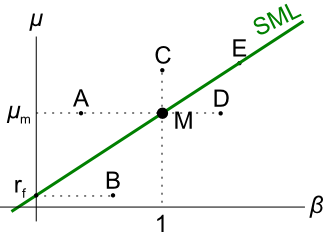
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
The accounting identity states that the book value of a company's assets (A) equals its liabilities (L) plus owners equity (OE), so A = L + OE.
The finance version states that the market value of a company's assets (V) equals the market value of its debt (D) plus equity (E), so V = D + E.
Therefore a business's assets can be seen as a portfolio of the debt and equity that fund the assets.
Let ##\sigma_\text{V total}^2## be the total variance of returns on assets, ##\sigma_\text{V syst}^2## be the systematic variance of returns on assets, and ##\sigma_\text{V idio}^2## be the idiosyncratic variance of returns on assets, and ##\rho_\text{D idio, E idio}## be the correlation between the idiosyncratic returns on debt and equity.
Which of the following equations is NOT correct?
A stock's required total return will increase when its:
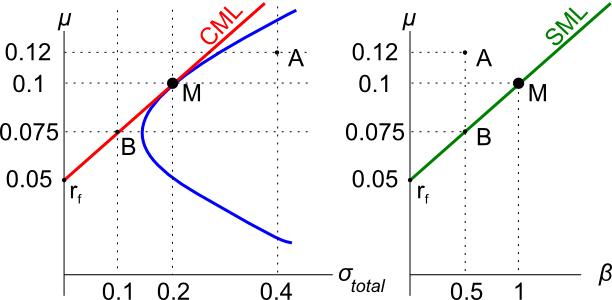
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
Which of the following is NOT a valid method for estimating the beta of a company's stock? Assume that markets are efficient, a long history of past data is available, the stock possesses idiosyncratic and market risk. The variances and standard deviations below denote total risks.
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
What do you think will be the stock's expected return over the next year, given as an effective annual rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
Over the last year, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. So ##r_{m} = (P_{0} - P_{-1})/P_{-1} = -0.01##, where the current time is zero and one year ago is time -1. The risk free rate was unchanged.
What do you think was the stock's historical return over the last year, given as an effective annual rate?
Question 776 market efficiency, systematic and idiosyncratic risk, beta, income and capital returns
Which of the following statements about returns is NOT correct? A stock's:
The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
A stock has a beta of 0.5.
In the last 5 minutes, the federal government unexpectedly raised taxes. Over this time the share market fell by 3%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
Question 239 income and capital returns, inflation, real and nominal returns and cash flows, interest only loan
A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.
From the bank's point of view, what is the long term expected nominal capital return of the loan asset?
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 295 inflation, real and nominal returns and cash flows, NPV
When valuing assets using discounted cash flow (net present value) methods, it is important to consider inflation. To properly deal with inflation:
(I) Discount nominal cash flows by nominal discount rates.
(II) Discount nominal cash flows by real discount rates.
(III) Discount real cash flows by nominal discount rates.
(IV) Discount real cash flows by real discount rates.
Which of the above statements is or are correct?
Question 407 income and capital returns, inflation, real and nominal returns and cash flows
A stock has a real expected total return of 7% pa and a real expected capital return of 2% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What is the nominal expected total return, capital return and dividend yield? The answers below are given in the same order.
In the 'Austin Powers' series of movies, the character Dr. Evil threatens to destroy the world unless the United Nations pays him a ransom (video 1, video 2). Dr. Evil makes the threat on two separate occasions:
- In 1969 he demands a ransom of $1 million (=10^6), and again;
- In 1997 he demands a ransom of $100 billion (=10^11).
If Dr. Evil's demands are equivalent in real terms, in other words $1 million will buy the same basket of goods in 1969 as $100 billion would in 1997, what was the implied inflation rate over the 28 years from 1969 to 1997?
The answer choices below are given as effective annual rates:
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
Question 522 income and capital returns, real and nominal returns and cash flows, inflation, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 2.5% pa. Inflation is expected to be 2.5% pa.
All of the above are effective nominal rates and investors believe that they will stay the same in perpetuity.
What are the property's expected real total, capital and income returns?
The answer choices below are given in the same order.
Question 523 income and capital returns, real and nominal returns and cash flows, inflation
A low-growth mature stock has an expected nominal total return of 6% pa and nominal capital return of 2% pa. Inflation is expected to be 3% pa.
All of the above are effective nominal rates and investors believe that they will stay the same in perpetuity.
What are the stock's expected real total, capital and income returns?
The answer choices below are given in the same order.
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 526 real and nominal returns and cash flows, inflation, no explanation
How can a nominal cash flow be precisely converted into a real cash flow?
Question 574 inflation, real and nominal returns and cash flows, NPV
What is the present value of a nominal payment of $100 in 5 years? The real discount rate is 10% pa and the inflation rate is 3% pa.
Question 852 gross domestic product, inflation, employment, no explanation
When the economy is booming (in an upswing), you tend to see: