A 2 year corporate bond yields 3% pa with a coupon rate of 5% pa, paid semi-annually.
Find the effective monthly rate, effective six month rate, and effective annual rate.
##r_\text{eff monthly}##, ##r_\text{eff 6 month}##, ##r_\text{eff annual}##.
Question 321 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 50 basis points due to high future GDP and inflation forecasts.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar will:
A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.
Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
A young lady is trying to decide if she should attend university or begin working straight away in her home town.
The young lady's grandma says that she should not go to university because she is less likely to marry the local village boy whom she likes because she will spend less time with him if she attends university.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The cost of not marrying the local village boy should be classified as:
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 6.5 years from now (first payment at t=6.5).
- A single payment of $500 in 4 years and 3 months (t=4.25) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 598 future, tailing the hedge, cross hedging
The standard deviation of monthly changes in the spot price of lamb is $0.015 per pound. The standard deviation of monthly changes in the futures price of live cattle is $0.012 per pound. The correlation between the spot price of lamb and the futures price of cattle is 0.4.
It is now January. A lamb producer is committed to selling 1,000,000 pounds of lamb in May. The spot price of live cattle is $0.30 per pound and the June futures price is $0.32 per pound. The spot price of lamb is $0.60 per pound.
The producer wants to use the June live cattle futures contracts to hedge his risk. Each futures contract is for the delivery of 50,000 pounds of cattle.
How many live cattle futures should the lamb farmer sell to hedge his risk? Round your answer to the nearest whole number of contracts.
A stock's required total return will increase when its:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.
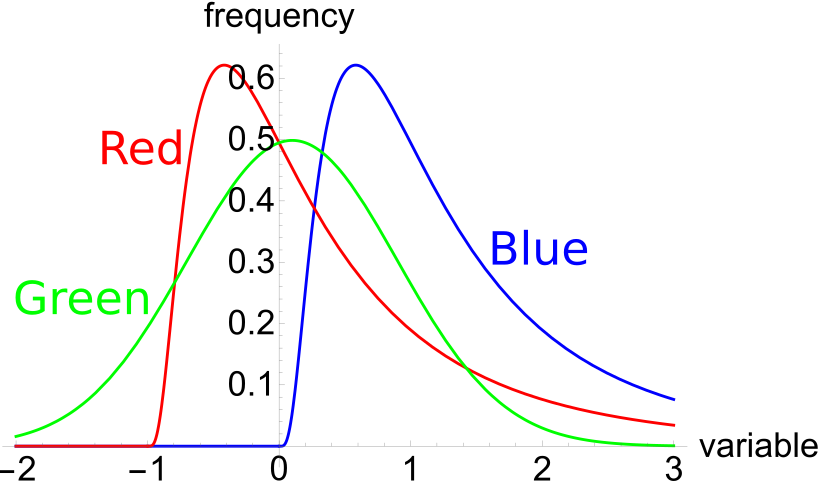
Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
A firm wishes to raise $50 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 6 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?