Fight Finance

Question 354  PE ratio, Multiples valuation

Which firms tend to have low forward-looking price-earnings (PE) ratios?

Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.

(a) Illiquid small private companies.

(b) High growth technology firms.

(c) Firms expected to have temporarily low earnings over the next year, but with higher earnings later.

(d) Firms with a very low level of systematic risk.

(e) Firms whose assets include a very large proportion of cash.

Question 463  PE ratio, Multiples valuation

Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).

If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?

Assume that:

• The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
• There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
• The large merged firm's earnings are the sum of the medium firms' earnings.
• The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
• Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.

(a) 300%.

(b) 200%

(c) 33.33%

(d) 30%

(e) 20%

Question 374  debt terminology

Which of the following statements is NOT equivalent to the yield on debt?

Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.

(a) Debt coupon rate.

(b) Required return on debt.

(c) Total return on debt.

(d) Opportunity cost of debt.

(e) Cost of debt capital.

Question 446  working capital decision, corporate financial decision theory

The working capital decision primarily affects which part of a business?

(a) Assets.

(b) Liabilities and owner's equity.

(c) Current assets and current liabilities.

(d) Dividends and buy backs.

(e) Net income, also known as earnings or net profit after tax.

Question 137  NPV, Annuity

The following cash flows are expected:

• 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
• 1 payment of $400 in 5 years and 6 months (t=5.5) from now.

What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?

(a) $513.80

(b) $525.36

(c) $541.50

(d) $605.48

(e) $704.69

Question 479  perpetuity with growth, DDM, NPV

Discounted cash flow (DCF) valuation prices assets by finding the present value of the asset's future cash flows. The single cash flow, annuity, and perpetuity equations are very useful for this.

Which of the following equations is the 'perpetuity with growth' equation?

(a) ##V_0=\dfrac{C_t}{(1+r)^t} ##

(b) ##V_0=\dfrac{C_1}{r}.\left(1-\dfrac{1}{(1+r)^T} \right)= \sum\limits_{t=1}^T \left( \dfrac{C_t}{(1+r)^t} \right) ##

(c) ##V_0=\dfrac{C_1}{r-g}.\left(1-\left(\dfrac{1+g}{1+r}\right)^T \right)= \sum\limits_{t=1}^T \left( \dfrac{C_t.(1+g)^t}{(1+r)^t} \right) ##

(d) ##V_0=\dfrac{C_1}{r} = \sum\limits_{t=1}^\infty \left( \dfrac{C_t}{(1+r)^t} \right) ##

(e) ##V_0=\dfrac{C_1}{r-g} = \sum\limits_{t=1}^\infty \left( \dfrac{C_t.(1+g)^t}{(1+r)^t} \right) ##

Question 3  DDM, income and capital returns

The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###

What is ##g##? The value ##g## is the long term expected:

(a) Income return of the stock.

(b) Capital return of the stock.

(c) Total return of the stock.

(d) Dividend yield of the stock.

(e) Price-earnings ratio of the stock.

Question 7  DDM

For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.

So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.

The required return of the stock is 15% pa.

Would you like to the share or politely ?

Question 216  DDM

A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.

What is the implied growth rate of the dividend per year?

(a) -0.8565

(b) -0.0500

(c) -0.0435

(d) 0.0000

(e) 0.1500

Question 497  income and capital returns, DDM, ex dividend date

A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.

What is the stock price today and what do you expect the stock price to be tomorrow, approximately?

(a) $200 today and $210 tomorrow.

(b) $210 today and $220 tomorrow.

(c) $220 today and $230 tomorrow.

(d) $210 today and $200 tomorrow.

(e) $220 today and $210 tomorrow.

Question 264  DDM

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

###P_0=\frac{d_1}{r-g}###

A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.

According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?

(a) ##P_{2.5}=P_0 (1+g)^{2.5} ##

(b) ##P_{2.5}=P_0 (1+r)^{2.5} ##

(c) ##P_{2.5}=P_0 (1+g)^2 (1+r)^{0.5} ##

(d) ##P_{2.5}=P_0 (1+r)^2 (1+g)^{0.5} ##

(e) ##P_{2.5}=P_0 (1+r)^3 (1+g)^{-0.5} ##

Question 39  DDM, perpetuity with growth

A stock is expected to pay the following dividends:

Cash Flows of a Stock
Time (yrs)	0	1	2	3	4	...
Dividend ($)	0.00	1.00	1.05	1.10	1.15	...

After year 4, the annual dividend will grow in perpetuity at 5% pa, so;

• the dividend at t=5 will be $1.15(1+0.05),
• the dividend at t=6 will be $1.15(1+0.05)^2, and so on.

The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?

(a) $25.6033

(b) $20.7476

(c) $20.0000

(d) $19.8835

(e) $18.3126

Question 207  income and capital returns, bond pricing, coupon rate, no explanation

For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?

Let: ##P_0## be the bond price now,

##F_T## be the bond's face value,

##T## be the bond's maturity in years,

##r_\text{total}## be the bond's total yield,

##r_\text{income}## be the bond's income yield,

##r_\text{capital}## be the bond's capital yield, and

##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.

(a) coupon rate = ##\dfrac{C_{0.5}+C_{1}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{total})^{0.5}+C_{1}}{P_0}##

(b) coupon rate = ##\dfrac{2 \times C_{0.5}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{capital})^{0.5}+C_{1}}{P_0}##

(c) coupon rate = ##\dfrac{2 \times C_{1}}{P_0}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}+C_{1}}{P_0}##

(d) coupon rate = ##\dfrac{2 \times C_{1}}{P_0}##, ##r_\text{income, 0 to 1}=\dfrac{2 \times C_{1}}{P_0}##

(e) coupon rate = ##\dfrac{2 \times C_{1}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{total})^{0.5}+C_{1}}{F_T}##

Question 213  income and capital returns, bond pricing, premium par and discount bonds

The coupon rate of a fixed annual-coupon bond is constant (always the same).

What can you say about the income return (##r_\text{income}##) of a fixed annual coupon bond? Remember that:

###r_\text{total} = r_\text{income} + r_\text{capital}###

###r_\text{total, 0 to 1} = \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0}###

Assume that there is no change in the bond's total annual yield to maturity from when it is issued to when it matures.

Select the most correct statement.

From its date of issue until maturity, the income return of a fixed annual coupon:

(a) Premium bond will increase.

(b) Premium bond will decrease.

(c) Premium bond will remain constant.

(d) Par bond will increase.

(e) Par bond will decrease.

Question 255  bond pricing

In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.

A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?

(a) 94.20452353

(b) 100

(c) 106

(d) 112

(e) The bond is priceless.

Question 538  bond pricing, income and capital returns, no explanation

Risk-free government bonds that have coupon rates greater than their yields:

(a) Are discount bonds.

(b) Have positive expected capital returns.

(c) Have higher expected income returns than total returns.

(d) Have prices less than their face values.

(e) Have significant credit risk.

Question 539  debt terminology, fully amortising loan, bond pricing

A 'fully amortising' loan can also be called a:

(a) Discount loan

(b) Par loan

(c) Premium loan

(d) Deferred repayment loan

(e) Interest only loan

Question 572  bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, forward interest rate, yield curve

In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:

###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###

Which of the following statements is NOT correct?

(a) ##r_{0-3}## is the three year spot rate, given as an effective annual rate.

(b) ##r_{0-1}## is the one year forward rate, given as an effective annual rate.

(c) ##r_{1-2}## is the one year forward rate one year ahead, given as an effective annual rate.

(d) ##r_{2-3}## is the one year forward rate two years ahead, given as an effective annual rate.

(e) ##r_{1-3} = \left((1+r_{1-2})(1+r_{2-3})\right)^{1/2}-1## is the two year forward rate, one year ahead, given as an effective annual rate.

Question 130  debt terminology

An 'interest rate' is the same thing as a 'yield'. or ?

Question 471  risk, accounting ratio

High risk firms in danger of bankruptcy tend to have:

(a) Low debt to assets ratios.

(b) High quick ratios.

(c) Low interest coverage ratios.

(d) Positive amounts of net working capital.

(e) High net profit margins.

Question 27  bill pricing, simple interest rate

A 180-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?

(a) $15,400,000.00

(b) $8,371,559.63

(c) $962,757.81

(d) $962,045.33

(e) $64,935.06

Question 20  NPV, APR, Annuity

Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.

If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?

(a) -648.51

(b) 60.28

(c) 70.88

(d) 125.51

(e) 200

Question 32  time calculation, APR

You really want to go on a back packing trip to Europe when you finish university. Currently you have $1,500 in the bank. Bank interest rates are 8% pa, given as an APR compounding per month. If the holiday will cost $2,000, how long will it take for your bank account to reach that amount?

(a) -3.74 years

(b) 1.81 years

(c) 3.33 years

(d) 3.61 years

(e) 3.74 years

Question 356  NPV, Annuity

Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.

What is the net present value (NPV) of borrowing from your friend?

Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.

(a) -$1,000

(b) $209.2132

(c) $644.7393

(d) $1,040.6721

(e) $1,400.611

Question 475  payout ratio, dividend, no explanation

The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.

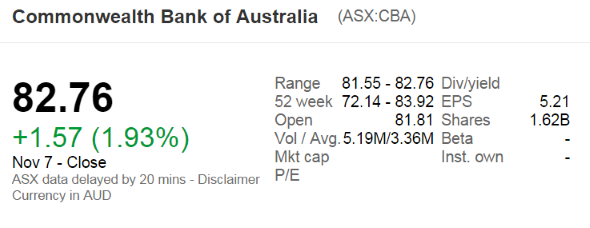
What was CBA's approximate payout ratio over the 2014 financial year?

Note that the firm's interim and final dividends were $1.83 and $2.18 respectively over the 2014 financial year.

(a) 2.48%

(b) 4.85%

(c) 77.00%

(d) 129.93%

(e) 247.53%

Question 245  foreign exchange rate, monetary policy, foreign exchange rate direct quote, no explanation

Investors expect Australia's central bank, the RBA, to leave the policy rate unchanged at their next meeting.

Then unexpectedly, the policy rate is reduced due to fears that Australia's GDP growth is slowing.

What do you expect to happen to Australia's exchange rate? Direct and indirect quotes are given from the perspective of an Australian.

The Australian dollar will:

(a) Appreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will increase.

(b) Depreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will decrease.

(c) Appreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will decrease.

(d) Depreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will increase.

(e) Depreciate against the USD, so the 'indirect quote' of the AUD (USD per AUD) will increase.

Question 41  DDM, income and capital returns

The following is the Dividend Discount Model (DDM) used to price stocks:

### P_0 = \frac{d_1}{r-g} ###

Assume that the assumptions of the DDM hold and that the time period is measured in years.

Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?

(a) ## d_1(1+g)^3 ##

(b) ## P_3(r-g) ##

(c) ## d_2(1+g)^2 ##

(d) ## P_0(1+g)^3(r-g) ##

(e) ## P_0(1+g)^2(r-g) ##

Question 51  DDM

A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.

Using the dividend discount model, what will be the share price?

(a) $50.00

(b) $50.50

(c) $100.00

(d) $111.11

(e) $112.22

Question 142  DDM, income and capital returns

When using the dividend discount model to price a stock:

### p_{0} = \frac{d_1}{r - g} ###

The growth rate of dividends (g):

(a) Is the stock's required return.

(b) Is the stock's expected total return.

(c) Is the stock's expected dividend return.

(d) Is the stock's expected real yield.

(e) Should be less than the expected GDP growth rate of the country where the company does business.

Question 148  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

### p_0 = \frac{d_1}{r - g} ###

Which expression is NOT equal to the expected dividend yield?

(a) ## r-g ##

(b) ## \dfrac{d_1}{p_0} ##

(c) ## \dfrac{d_5}{p_4} ##

(d) ## \dfrac{d_5(1+g)^2}{p_6} ##

(e) ## \dfrac{d_3}{p_0(1+r)^2} ##

Question 545  income and capital returns, fully amortising loan, no explanation

Which of the following statements about the capital and income returns of a 25 year fully amortising loan asset is correct?

Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.

Over the 25 years from issuance to maturity, a fully amortising loan's expected annual effective:

(a) Income and capital returns both rise.

(b) Income and capital returns both fall.

(c) Income return rises and its capital return falls.

(d) Income return falls and its capital return rises.

(e) Income and capital returns are constant.

Question 486  capital budgeting, opportunity cost, sunk cost

A young lady is trying to decide if she should attend university. Her friends say that she should go to university because she is more likely to meet a clever young man than if she begins full time work straight away.

What's the correct way to classify this item from a capital budgeting perspective when trying to find the Net Present Value of going to university rather than working?

The opportunity to meet a desirable future spouse should be classified as:

(a) A sunk cost.

(b) An opportunity cost.

(c) A negative side effect.

(d) A positive side effect.

(e) A depreciation expense.

Question 514  corporate financial decision theory, idiom

The expression 'cash is king' emphasizes the importance of having enough cash to pay your short term debts to avoid bankruptcy. Which business decision is this expression most closely related to?

(a) Investment decision.

(b) Financing decision.

(c) Working capital decision.

(d) Payout policy decision.

(e) Capital or labour decision.

Question 126  IRR

What is the Internal Rate of Return (IRR) of the project detailed in the table below?

Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.

Project Cash Flows
Time (yrs)	Cash flow ($)
0	-100
1	0
2	121

(a) 0.21

(b) 0.105

(c) 0.1111

(d) 0.1

(e) 0

Question 140  IRR, NPV, profitability index

A project has an internal rate of return (IRR) which is greater than its required return. Select the most correct statement.

(a) The NPV will be negative and the profitability index will be less than 1.

(b) The NPV will be positive and the profitability index will be more than 1.

(c) The payback period will be positive and the Accounting Rate of Return will be more than the target return.

(d) The NPV will be positive and the profitability index will be negative.

(e) The NPV will be negative and the profitability index will be positive.

Question 189  IRR

A project has the following cash flows:

Project Cash Flows
Time (yrs)	Cash flow ($)
0	-400
1	0
2	500

The required return on the project is 10%, given as an effective annual rate.

What is the Internal Rate of Return (IRR) of this project? The following choices are effective annual rates. Assume that the cash flows shown in the table are paid all at once at the given point in time.

(a) 0.2500

(b) 0.2000

(c) 0.1180

(d) 0.1000

(e) 0.1056

Question 489  NPV, IRR, pay back period, DDM

A firm is considering a business project which costs $11m now and is expected to pay a constant $1m at the end of every year forever.

Assume that the initial $11m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.

Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?

(a) The NPV is negative $1m.

(b) The IRR is 9.09% pa, less than the 10% cost of capital.

(c) The payback period is infinite, the project will never pay itself off.

(d) The project should be rejected.

(e) If the project is accepted then the market value of the firm's assets will fall by $1m.

Question 469  franking credit, personal tax on dividends, imputation tax system, no explanation

A firm pays a fully franked cash dividend of $70 to one of its Australian shareholders who has a personal marginal tax rate of 45%. The corporate tax rate is 30%.

What will be the shareholder's personal tax payable due to the dividend payment?

(a) $13.50

(b) $15.00

(c) $30.00

(d) $31.50

(e) $45.00

Question 187  fully amortising loan, APR

You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.

How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.

(a) 169,672.58,     90,724.32

(b) 166,791.61,     90,073.45

(c) 166,791.61,     139,580.77

(d) 165,177.97,     88,321.04

(e) 165,177.97,     137,639.05

Question 234  debt terminology

An 'interest only' loan can also be called a:

(a) Discount loan

(b) Par loan

(c) Premium loan

(d) Deferred repayment loan

(e) Fully amortising loan.

Question 239  income and capital returns, inflation, real and nominal returns and cash flows, interest only loan

A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.

From the bank's point of view, what is the long term expected nominal capital return of the loan asset?

(a) Approximately 6%.

(b) Approximately 4%.

(c) Approximately 2%.

(d) Approximately 0%.

(e) Approximately -2%.

Question 263  DDM, income and capital returns

A company's shares just paid their annual dividend of $2 each.

The stock price is now $40 (just after the dividend payment). The annual dividend is expected to grow by 3% every year forever. The assumptions of the dividend discount model are valid for this company.

What do you expect the effective annual dividend yield to be in 3 years (dividend yield from t=3 to t=4)?

(a) 0.03

(b) 0.0409

(c) 0.044

(d) 0.05

(e) 0.0515

Question 331  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

### p_0= \frac{c_1}{r-g} ###

Which expression is equal to the expected dividend return?

(a) ##(c_1/p_0 ) -1##

(b) ##(p_1/p_0) -1##

(c) ##(c_5/c_4) -1##

(d) ##c_3/p_2##

(e) ##(p_1-p_0)/p_0##

Question 49  inflation, real and nominal returns and cash flows, APR, effective rate

In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.

The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.

What is the real yield on these bonds, given as an APR compounding every 6 months?

(a) 0.3086%

(b) 0.6171%

(c) 0.6181%

(d) 0.6239%

(e) 0.6300%

Question 141  time calculation, APR, effective rate

You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.

How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.

(a) 23.62

(b) 25.00

(c) 26.60

(d) 26.77

(e) 55.24

Question 380  leverage, capital structure

The "interest expense" on a company's annual income statement is equal to the cash interest payments (but not principal payments) made to debt holders during the year. or ?

Question 519  DDM

A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.

Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.

Calculate the current stock price.

(a) $10

(b) $12.254902

(c) $12.5

(d) $12.75

(e) $13.75

Question 293  covariance, correlation, portfolio risk

All things remaining equal, the higher the correlation of returns between two stocks:

(a) The more diversification is possible when those stocks are combined in a portfolio.

(b) The lower the variance of returns of an equally-weighted portfolio of those stocks.

(c) The lower the volatility of returns of an equal-weighted portfolio of those stocks.

(d) The higher the covariance between those stocks' returns.

(e) The more likely that when one stock has a positive return, the other has a negative return.

Question 429  takeover

In a takeover deal where the offer is 100% scrip (shares), the merged firm's number of shares will be equal to the sum of the acquirer and target firms' original number of shares. or ?

Question 398  financial distress, capital raising, leverage, capital structure, NPV

A levered firm has zero-coupon bonds which mature in one year and have a combined face value of $9.9m.

Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.

In one year the firm's assets will be worth:

• $13.2m with probability 0.5 in the good state of the world, or
• $6.6m with probability 0.5 in the bad state of the world.

A new project presents itself which requires an investment of $2m and will provide a certain cash flow of $3.3m in one year.

The firm doesn't have any excess cash to make the initial $2m investment, but the funds can be raised from shareholders through a fairly priced rights issue. Ignore all transaction costs.

Should shareholders vote to proceed with the project and equity raising? What will be the gain in shareholder wealth if they decide to proceed?

(a) Yes, $3m

(b) Yes, $1.5m

(c) Yes, $1m

(d) No, -$0.5m

(e) No, -$1.5m

Question 79  CAPM, risk

Which statement is the most correct?

(a) The risk free rate has zero systematic risk and zero idiosyncratic risk.

(b) The market portfolio has zero idiosyncratic risk.

(c) The market portfolio has zero systematic risk.

(d) a and b are true.

(e) a and c are true.

Question 92  CAPM, SML, CML

Which statement(s) are correct?

(i) All stocks that plot on the Security Market Line (SML) are fairly priced.

(ii) All stocks that plot above the Security Market Line (SML) are overpriced.

(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.

Select the most correct response:

(a) Only (i) is true.

(b) Only (ii) is true.

(c) Only (iii) is true.

(d) All statements (i), (ii) and (iii) are true.

(e) Only statements (i) and (iii) are true.

Question 111  portfolio risk, correlation

All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:

(a) The correlation between the stocks' returns rise.

(b) The correlation between the stocks' returns decline.

(c) The portfolio standard deviation declines.

(d) Both stocks' individual variances decline.

(e) Both stocks' individual standard deviations decline.

Question 116  capital structure, CAPM

A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.

According to the Capital Asset Pricing Model (CAPM), which statement is correct?

(a) The beta of the firm's assets will increase.

(b) The beta of the firm's assets will decrease.

(c) The beta of the firm's equity will increase.

(d) The beta of the firm's equity will decrease.

(e) The beta of the firm's equity will be unchanged.

Question 235  SML, NPV, CAPM, risk

The security market line (SML) shows the relationship between beta and expected return.

Investment projects that plot on the SML would have:

(a) A positive NPV and should be accepted.

(b) A zero NPV.

(c) A negative NPV and should be rejected.

(d) A large amount of diversifiable risk.

(e) Zero diversifiable risk.

Question 248  CAPM, DDM, income and capital returns

The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):

###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###

Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:

###r_\text{total}=r_\text{income}+r_\text{capital}###

So the total return of an asset is the income component plus the capital or price growth component.

Another way to break up total return is to use the Capital Asset Pricing Model:

###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###

###r_\text{total}=r_\text{time value}+r_\text{risk premium}###

So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.

Using the above theory and your general knowledge, which of the below equations, if any, are correct?

(I) ##r_\text{income}=r_\text{time value}##

(II) ##r_\text{income}=r_\text{risk premium}##

(III) ##r_\text{capital}=r_\text{time value}##

(IV) ##r_\text{capital}=r_\text{risk premium}##

(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##

Which of the equations are correct?

(a) I, IV and V only.

(b) II, III and V only.

(c) V only.

(d) All are true.

(e) None are true.

Question 271  CAPM, option, risk, systematic risk, systematic and idiosyncratic risk

All things remaining equal, according to the capital asset pricing model, if the systematic variance of an asset increases, its required return will increase and its price will decrease.
If the idiosyncratic variance of an asset increases, its price will be unchanged.

What is the relationship between the price of a call or put option and the total, systematic and idiosyncratic variance of the underlying asset that the option is based on? Select the most correct answer.

Call and put option prices increase when the:

(a) Systematic variance of the underlying asset increases.

(b) Idiosyncratic variance of the underlying asset increases.

(c) Systematic, idiosyncratic or total variance of the underlying asset increases.

(d) Systematic variance of the underlying asset decreases.

(e) Systematic, idiosyncratic or total variance of the underlying asset decreases.

Question 338  market efficiency, CAPM, opportunity cost, technical analysis

A man inherits $500,000 worth of shares.

He believes that by learning the secrets of trading, keeping up with the financial news and doing complex trend analysis with charts that he can quit his job and become a self-employed day trader in the equities markets.

What is the expected gain from doing this over the first year? Measure the net gain in wealth received at the end of this first year due to the decision to become a day trader. Assume the following:

• He earns $60,000 pa in his current job, paid in a lump sum at the end of each year.
• He enjoys examining share price graphs and day trading just as much as he enjoys his current job.
• Stock markets are weak form and semi-strong form efficient.
• He has no inside information.
• He makes 1 trade every day and there are 250 trading days in the year. Trading costs are $20 per trade. His broker invoices him for the trading costs at the end of the year.
• The shares that he currently owns and the shares that he intends to trade have the same level of systematic risk as the market portfolio.
• The market portfolio's expected return is 10% pa.

Measure the net gain over the first year as an expected wealth increase at the end of the year.

(a) $110,000

(b) $50,000

(c) $45,000

(d) -$15,000

(e) -$65,000

Question 408  leverage, portfolio beta, portfolio risk, real estate, CAPM

You just bought a house worth $1,000,000. You financed it with an $800,000 mortgage loan and a deposit of $200,000.

You estimate that:

• The house has a beta of 1;
• The mortgage loan has a beta of 0.2.

What is the beta of the equity (the $200,000 deposit) that you have in your house?

Also, if the risk free rate is 5% pa and the market portfolio's return is 10% pa, what is the expected return on equity in your house? Ignore taxes, assume that all cash flows (interest payments and rent) were paid and received at the end of the year, and all rates are effective annual rates.

(a) The beta of equity is 5 and the expected return on equity is 30% pa.

(b) The beta of equity is 4.2 and the expected return on equity is 26% pa.

(c) The beta of equity is 0.86 and the expected return on equity is 9.3% pa.

(d) The beta of equity is 1 and the expected return on equity is 10% pa.

(e) The beta of equity is 0.6 and the expected return on equity is 8% pa.

Question 173  CFFA

Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Candys Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	200
COGS	50
Operating expense	10
Depreciation	20
Interest expense	10
Income before tax	110
Tax at 30%	33
Net income	77

Candys Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	220	180
PPE
Cost	300	340
Accumul. depr.	60	40
Carrying amount	240	300
Total assets	460	480
Liabilities
Current liabilities	175	190
Non-current liabilities	135	130
Owners' equity
Retained earnings	50	60
Contributed equity	100	100
Total L and OE	460	480

 

Note: all figures are given in millions of dollars ($m).

(a) 242

(b) 182

(c) 112

(d) 92

(e) 52

Question 238  CFFA, leverage, interest tax shield

A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.

Ignoring the costs of financial distress, which of the following statements is NOT correct:

(a) The company is increasing its debt-to-assets and debt-to-equity ratios. These are types of 'leverage' or 'gearing' ratios.

(b) The company will pay less tax to the government due to the benefit of interest tax shields.

(c) The company's net income, also known as earnings or net profit after tax, will fall.

(d) The company's expected levered firm free cash flow (FFCF or CFFA) will be higher due to tax shields.

(e) The company's expected levered equity free cash flow (EFCF) will not change.

Question 350  CFFA

Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Sidebar Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	405
COGS	100
Depreciation	34
Rent expense	22
Interest expense	39
Taxable Income	210
Taxes at 30%	63
Net income	147

Sidebar Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Cash	0	0
Inventory	70	50
Trade debtors	11	16
Rent paid in advance	4	3
PPE	700	680
Total assets	785	749
Trade creditors	11	19
Bond liabilities	400	390
Contributed equity	220	220
Retained profits	154	120
Total L and OE	785	749

 

Note: All figures are given in millions of dollars ($m).

The cash flow from assets was:

(a) $138m

(b) $142m

(c) $143m

(d) $172m

(e) $176m

Question 208  CFFA

Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

UniBar Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	80
COGS	40
Operating expense	15
Depreciation	10
Interest expense	5
Income before tax	10
Tax at 30%	3
Net income	7

UniBar Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	120	90
PPE
Cost	360	320
Accumul. depr.	40	30
Carrying amount	320	290
Total assets	440	380
Liabilities
Current liabilities	110	60
Non-current liabilities	190	180
Owners' equity
Retained earnings	95	95
Contributed equity	45	45
Total L and OE	440	380

 

Note: all figures are given in millions of dollars ($m).

(a) 12

(b) 2

(c) -8

(d) -18

(e) 48

Question 361  CFFA

Over the next year, the management of an unlevered company plans to:

• Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
• Pay dividends of $1m.
• Complete a $1.3m share buy-back.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2m

(b) $1m

(c) $0.4m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 351  CFFA

Over the next year, the management of an unlevered company plans to:

• Achieve firm free cash flow (FFCF or CFFA) of $1m.
• Pay dividends of $1.8m
• Complete a $1.3m share buy-back.
• Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2.1m

(b) $1.3m

(c) $0.8m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 67  CFFA, interest tax shield

Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###

###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###

What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?

Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.

(a) ##D(1+r_D)##

(b) ##D/(1+r_D) ##

(c) ##D.r_D ##

(d) ##D / r_D##

(e) ##NI.r_D##

Question 68  WACC, CFFA, capital budgeting

A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?

Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.

(a) The manufacturing firm's before-tax WACC.

(b) The manufacturing firm's after-tax WACC.

(c) A services firm's before-tax WACC, assuming that the services firm has the same debt-to-assets ratio as the manufacturing firm.

(d) A services firm's after-tax WACC, assuming that the services firm has the same debt-to-assets ratio as the manufacturing firm.

(e) The services firm's levered cost of equity.

Question 303  WACC, CAPM, CFFA

There are many different ways to value a firm's assets. Which of the following will NOT give the correct market value of a levered firm's assets ##(V_L)##? Assume that:

• The firm is financed by listed common stock and vanilla annual fixed coupon bonds, which are both traded in a liquid market.
• The bonds' yield is equal to the coupon rate, so the bonds are issued at par. The yield curve is flat and yields are not expected to change. When bonds mature they will be rolled over by issuing the same number of new bonds with the same expected yield and coupon rate, and so on forever.
• Tax rates on the dividends and capital gains received by investors are equal, and capital gains tax is paid every year, even on unrealised gains regardless of when the asset is sold.
• There is no re-investment of the firm's cash back into the business. All of the firm's excess cash flow is paid out as dividends so real growth is zero.
• The firm operates in a mature industry with zero real growth.
• All cash flows and rates in the below equations are real (not nominal) and are expected to be stable forever. Therefore the perpetuity equation with no growth is suitable for valuation.

(a) ##V_L = n_\text{shares}.P_\text{share} + n_\text{bonds}.P_\text{bond}##

(b) ##V_L = n_\text{shares}.\dfrac{\text{Dividend per share}}{r_f + \beta_{EL}(r_m - r_f)} + n_\text{bonds}.\dfrac{\text{Coupon per bond}}{r_f + \beta_D(r_m - r_f)}##

(c) ##V_L = \dfrac{\text{CFFA}_{L}}{r_\text{WACC before tax}}##

(d) ##V_L = \dfrac{\text{CFFA}_{U}}{r_\text{WACC after tax}}##

(e) ##V_L = \dfrac{\text{CFFA}_{L}}{r_\text{WACC after tax}}##

Where:

###r_\text{WACC before tax} = r_D.\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital before tax}### ###r_\text{WACC after tax} = r_D.(1-t_c).\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital after tax}### ###NI_L=(Rev-COGS-FC-Depr-\mathbf{IntExp}).(1-t_c) = \text{Net Income Levered}### ###CFFA_L=NI_L+Depr-CapEx - \varDelta NWC+\mathbf{IntExp} = \text{Cash Flow From Assets Levered}### ###NI_U=(Rev-COGS-FC-Depr).(1-t_c) = \text{Net Income Unlevered}### ###CFFA_U=NI_U+Depr-CapEx - \varDelta NWC= \text{Cash Flow From Assets Unlevered}###