Which firms tend to have high forward-looking price-earnings (PE) ratios?
Government bonds currently have a return of 5% pa. A stock has an expected return of 6% pa and the market return is 7% pa. What is the beta of the stock?
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
Government bonds currently have a return of 5%. A stock has a beta of 2 and the market return is 7%. What is the expected return of the stock?
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
Treasury bonds currently have a return of 5% pa. A stock has a beta of 0.5 and the market return is 10% pa. What is the expected return of the stock?
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
Which statement(s) are correct?
(i) All stocks that plot on the Security Market Line (SML) are fairly priced.
(ii) All stocks that plot above the Security Market Line (SML) are overpriced.
(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.
Select the most correct response:
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
Question 104 CAPM, payout policy, capital structure, Miller and Modigliani, risk
Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.
For a firm operating in this perfect world, which statement(s) are correct?
(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.
(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.
(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.
Select the most correct response:
A fairly priced stock has an expected return of 15% pa. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the beta of the stock?
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
A fairly priced stock has a beta that is the same as the market portfolio's beta. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the expected return of the stock?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the price of the stock now?
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):
###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###
Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:
###r_\text{total}=r_\text{income}+r_\text{capital}###
So the total return of an asset is the income component plus the capital or price growth component.
Another way to break up total return is to use the Capital Asset Pricing Model:
###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###
###r_\text{total}=r_\text{time value}+r_\text{risk premium}###
So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.
Using the above theory and your general knowledge, which of the below equations, if any, are correct?
(I) ##r_\text{income}=r_\text{time value}##
(II) ##r_\text{income}=r_\text{risk premium}##
(III) ##r_\text{capital}=r_\text{time value}##
(IV) ##r_\text{capital}=r_\text{risk premium}##
(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##
Which of the equations are correct?
There are many different ways to value a firm's assets. Which of the following will NOT give the correct market value of a levered firm's assets ##(V_L)##? Assume that:
- The firm is financed by listed common stock and vanilla annual fixed coupon bonds, which are both traded in a liquid market.
- The bonds' yield is equal to the coupon rate, so the bonds are issued at par. The yield curve is flat and yields are not expected to change. When bonds mature they will be rolled over by issuing the same number of new bonds with the same expected yield and coupon rate, and so on forever.
- Tax rates on the dividends and capital gains received by investors are equal, and capital gains tax is paid every year, even on unrealised gains regardless of when the asset is sold.
- There is no re-investment of the firm's cash back into the business. All of the firm's excess cash flow is paid out as dividends so real growth is zero.
- The firm operates in a mature industry with zero real growth.
- All cash flows and rates in the below equations are real (not nominal) and are expected to be stable forever. Therefore the perpetuity equation with no growth is suitable for valuation.
Where:
###r_\text{WACC before tax} = r_D.\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital before tax}### ###r_\text{WACC after tax} = r_D.(1-t_c).\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital after tax}### ###NI_L=(Rev-COGS-FC-Depr-\mathbf{IntExp}).(1-t_c) = \text{Net Income Levered}### ###CFFA_L=NI_L+Depr-CapEx - \varDelta NWC+\mathbf{IntExp} = \text{Cash Flow From Assets Levered}### ###NI_U=(Rev-COGS-FC-Depr).(1-t_c) = \text{Net Income Unlevered}### ###CFFA_U=NI_U+Depr-CapEx - \varDelta NWC= \text{Cash Flow From Assets Unlevered}###A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
Question 338 market efficiency, CAPM, opportunity cost, technical analysis
A man inherits $500,000 worth of shares.
He believes that by learning the secrets of trading, keeping up with the financial news and doing complex trend analysis with charts that he can quit his job and become a self-employed day trader in the equities markets.
What is the expected gain from doing this over the first year? Measure the net gain in wealth received at the end of this first year due to the decision to become a day trader. Assume the following:
- He earns $60,000 pa in his current job, paid in a lump sum at the end of each year.
- He enjoys examining share price graphs and day trading just as much as he enjoys his current job.
- Stock markets are weak form and semi-strong form efficient.
- He has no inside information.
- He makes 1 trade every day and there are 250 trading days in the year. Trading costs are $20 per trade. His broker invoices him for the trading costs at the end of the year.
- The shares that he currently owns and the shares that he intends to trade have the same level of systematic risk as the market portfolio.
- The market portfolio's expected return is 10% pa.
Measure the net gain over the first year as an expected wealth increase at the end of the year.
Diversification in a portfolio of two assets works best when the correlation between their returns is:
The following table shows a sample of historical total returns of shares in two different companies A and B.
| Stock Returns | ||
| Total effective annual returns | ||
| Year | ##r_A## | ##r_B## |
| 2007 | 0.2 | 0.4 |
| 2008 | 0.04 | -0.2 |
| 2009 | -0.1 | -0.3 |
| 2010 | 0.18 | 0.5 |
What is the historical sample covariance (##\hat{\sigma}_{A,B}##) and correlation (##\rho_{A,B}##) of stock A and B's total effective annual returns?
All things remaining equal, the higher the correlation of returns between two stocks:
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
Question 100 market efficiency, technical analysis, joint hypothesis problem
A company selling charting and technical analysis software claims that independent academic studies have shown that its software makes significantly positive abnormal returns. Assuming the claim is true, which statement(s) are correct?
(I) Weak form market efficiency is broken.
(II) Semi-strong form market efficiency is broken.
(III) Strong form market efficiency is broken.
(IV) The asset pricing model used to measure the abnormal returns (such as the CAPM) had mis-specification error so the returns may not be abnormal but rather fair for the level of risk.
Select the most correct response:
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
Question 119 market efficiency, fundamental analysis, joint hypothesis problem
Your friend claims that by reading 'The Economist' magazine's economic news articles, she can identify shares that will have positive abnormal expected returns over the next 2 years. Assuming that her claim is true, which statement(s) are correct?
(i) Weak form market efficiency is broken.
(ii) Semi-strong form market efficiency is broken.
(iii) Strong form market efficiency is broken.
(iv) The asset pricing model used to measure the abnormal returns (such as the CAPM) is either wrong (mis-specification error) or is measured using the wrong inputs (data errors) so the returns may not be abnormal but rather fair for the level of risk.
Select the most correct response:
Select the most correct statement from the following.
'Chartists', also known as 'technical traders', believe that:
Fundamentalists who analyse company financial reports and news announcements (but who don't have inside information) will make positive abnormal returns if:
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
A firm's weighted average cost of capital before tax (##r_\text{WACC before tax}##) would increase due to:
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of equity to raise money for new projects of similar systematic risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
Question 99 capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.
Assume that:
- The firm and individual investors can borrow at the same rate and have the same tax rates.
- The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
- There are no market frictions relating to debt such as asymmetric information or transaction costs.
- Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.
According to Miller and Modigliani's theory, which statement is correct?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| UniBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 80 | |
| COGS | 40 | |
| Operating expense | 15 | |
| Depreciation | 10 | |
| Interest expense | 5 | |
| Income before tax | 10 | |
| Tax at 30% | 3 | |
| Net income | 7 | |
| UniBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 90 |
| PPE | ||
| Cost | 360 | 320 |
| Accumul. depr. | 40 | 30 |
| Carrying amount | 320 | 290 |
| Total assets | 440 | 380 |
| Liabilities | ||
| Current liabilities | 110 | 60 |
| Non-current liabilities | 190 | 180 |
| Owners' equity | ||
| Retained earnings | 95 | 95 |
| Contributed equity | 45 | 45 |
| Total L and OE | 440 | 380 |
Note: all figures are given in millions of dollars ($m).
Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Piano Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 310 | |
| COGS | 185 | |
| Operating expense | 20 | |
| Depreciation | 15 | |
| Interest expense | 10 | |
| Income before tax | 80 | |
| Tax at 30% | 24 | |
| Net income | 56 | |
| Piano Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 240 | 230 |
| PPE | ||
| Cost | 420 | 400 |
| Accumul. depr. | 50 | 35 |
| Carrying amount | 370 | 365 |
| Total assets | 610 | 595 |
| Liabilities | ||
| Current liabilities | 180 | 190 |
| Non-current liabilities | 290 | 265 |
| Owners' equity | ||
| Retained earnings | 90 | 90 |
| Contributed equity | 50 | 50 |
| Total L and OE | 610 | 595 |
Note: all figures are given in millions of dollars ($m).
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| World Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 300 | |
| COGS | 150 | |
| Operating expense | 50 | |
| Depreciation | 40 | |
| Interest expense | 10 | |
| Taxable income | 50 | |
| Tax at 30% | 15 | |
| Net income | 35 | |
| World Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 200 | 230 |
| PPE | ||
| Cost | 400 | 400 |
| Accumul. depr. | 75 | 35 |
| Carrying amount | 325 | 365 |
| Total assets | 525 | 595 |
| Liabilities | ||
| Current liabilities | 150 | 205 |
| Non-current liabilities | 235 | 250 |
| Owners' equity | ||
| Retained earnings | 100 | 100 |
| Contributed equity | 40 | 40 |
| Total L and OE | 525 | 595 |
Note: all figures above and below are given in millions of dollars ($m).
A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.
Ignoring the costs of financial distress, which of the following statements is NOT correct:
Value the following business project to manufacture a new product.
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $3m | |
| Expected sale price of equipment at end of project | $0.6m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense per year | 0 | |
| Tax rate | 30% | |
| Weighted average cost of capital after tax per annum | 10% | |
Notes
- The firm's current assets and current liabilities are $3m and $2m respectively right now. This net working capital will not be used in this project, it will be used in other unrelated projects.
Due to the project, current assets (mostly inventory) will grow by $2m initially (at t = 0), and then by $0.2m at the end of the first year (t=1).
Current liabilities (mostly trade creditors) will increase by $0.1m at the end of the first year (t=1).
At the end of the project, the net working capital accumulated due to the project can be sold for the same price that it was bought. - The project cost $0.5m to research which was incurred one year ago.
Assumptions
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 3% pa.
- All rates are given as effective annual rates.
- The business considering the project is run as a 'sole tradership' (run by an individual without a company) and is therefore eligible for a 50% capital gains tax discount when the equipment is sold, as permitted by the Australian Tax Office.
What is the expected net present value (NPV) of the project?
Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Scubar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 60 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 90 | |
| Taxes at 30% | 27 | |
| Net income | 63 | |
| Scubar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 60 | 50 |
| Trade debtors | 19 | 6 |
| Rent paid in advance | 3 | 2 |
| PPE | 420 | 400 |
| Total assets | 502 | 458 |
| Trade creditors | 10 | 8 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 130 | 130 |
| Retained profits | 162 | 130 |
| Total L and OE | 502 | 458 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
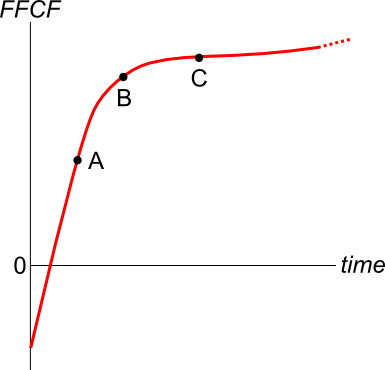
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
An old company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
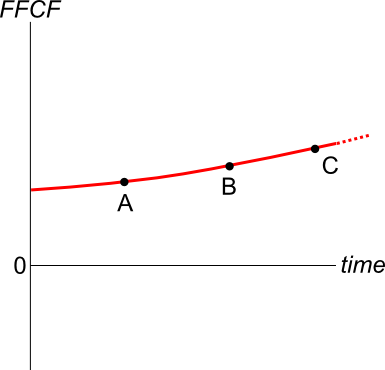
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
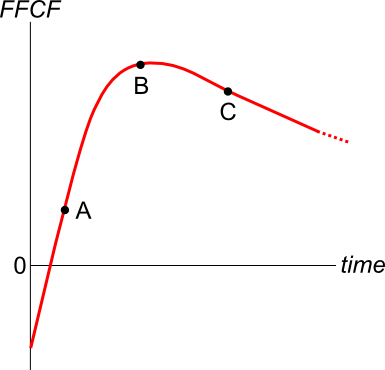
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Achieve firm free cash flow (FFCF or CFFA) of $1m.
- Pay dividends of $1.8m
- Complete a $1.3m share buy-back.
- Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Find Ching-A-Lings Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Ching-A-Lings Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 20 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 30 | |
| Taxes at 30% | 9 | |
| Net income | 21 | |
| Ching-A-Lings Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 49 | 38 |
| Trade debtors | 14 | 2 |
| Rent paid in advance | 5 | 5 |
| PPE | 400 | 400 |
| Total assets | 468 | 445 |
| Trade creditors | 4 | 10 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 145 | 145 |
| Retained profits | 119 | 100 |
| Total L and OE | 468 | 445 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
- Pay dividends of $1m.
- Complete a $1.3m share buy-back.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.
Which of the below FFCF formulas include the interest tax shield in the cash flow?
###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use earnings before interest and tax (EBIT).
###\begin{aligned} FFCF &= (EBIT)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ \end{aligned} \\###
One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?
You may assume:
- the value of debt (D) is constant through time,
- The cost of debt and the yield on debt are equal and given by ##r_D##.
- the appropriate rate to discount interest tax shields is ##r_D##.
- ##\text{IntExp}=D.r_D##
Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.
For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.
The advantage of negative gearing is an example of the benefits of:
Question 241 Miller and Modigliani, leverage, payout policy, diversification, NPV
One of Miller and Modigliani's (M&M's) important insights is that a firm's managers should not try to achieve a particular level of leverage in a world with zero taxes and perfect information since investors can make their own leverage. Therefore corporate capital structure policy is irrelevant since investors can achieve their own desired leverage at the personal level by borrowing or lending on their own.
This principal of 'home-made' or 'do-it-yourself' leverage can also be applied to other topics. Read the following statements to decide which are true:
(I) Payout policy: a firm's managers should not try to achieve a particular pattern of equity payout.
(II) Agency costs: a firm's managers should not try to minimise agency costs.
(III) Diversification: a firm's managers should not try to diversify across industries.
(IV) Shareholder wealth: a firm's managers should not try to maximise shareholders' wealth.
Which of the above statement(s) are true?
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the expected return of the above portfolio?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Covariance ##(\sigma_{A,B})## | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the standard deviation (not variance) of the above portfolio? Note that the stocks' covariance is given, not correlation.
Which of the following statements about short-selling is NOT true?
A company has:
- 50 million shares outstanding.
- The market price of one share is currently $6.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts believe that the company's ordinary shares have a beta of 2.
- The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
- The company's debentures are publicly traded and their market price is equal to 90% of their face value.
- The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.
A company has:
- 140 million shares outstanding.
- The market price of one share is currently $2.
- The company's debentures are publicly traded and their market price is equal to 93% of the face value.
- The debentures have a total face value of $50,000,000 and the current yield to maturity of corporate debentures is 12% per annum.
- The risk-free rate is 8.50% and the market return is 13.7%.
- Market analysts estimated that the company's stock has a beta of 0.90.
- The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC) in a classical tax system?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A company has:
- 10 million common shares outstanding, each trading at a price of $90.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant dividend of 9% of par. They currently trade at a price of $120 each.
- Debentures that have a total face value of $60,000,000 and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 90% of their face value.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts estimate that the company's common stock has a beta of 1.2. The corporate tax rate is 30%.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A company has:
- 100 million ordinary shares outstanding which are trading at a price of $5 each. Market analysts estimated that the company's ordinary stock has a beta of 1.5. The risk-free rate is 5% and the market return is 10%.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant annual dividend of 9% of par. The next dividend will be paid in one year. Assume that all preference dividends will be paid when promised. They currently trade at a price of $90 each.
- Debentures that have a total face value of $200 million and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 110% of their face value.
The corporate tax rate is 30%. All returns and yields are given as effective annual rates.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?
Let the variance of returns for a share per month be ##\sigma_\text{monthly}^2##.
What is the formula for the variance of the share's returns per year ##(\sigma_\text{yearly}^2)##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
You really want to go on a back packing trip to Europe when you finish university. Currently you have $1,500 in the bank. Bank interest rates are 8% pa, given as an APR compounding per month. If the holiday will cost $2,000, how long will it take for your bank account to reach that amount?
Question 64 inflation, real and nominal returns and cash flows, APR, effective rate
In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.
The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Question 180 equivalent annual cash flow, inflation, real and nominal returns and cash flows
Details of two different types of light bulbs are given below:
- Low-energy light bulbs cost $3.50, have a life of nine years, and use about $1.60 of electricity a year, paid at the end of each year.
- Conventional light bulbs cost only $0.50, but last only about a year and use about $6.60 of energy a year, paid at the end of each year.
The real discount rate is 5%, given as an effective annual rate. Assume that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the Equivalent Annual Cost (EAC) of the low-energy and conventional light bulbs. The below choices are listed in that order.
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
For a price of $13, Carla will sell you a share paying a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $6, Carlos will sell you a share which will pay a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $102, Andrea will sell you a share which just paid a dividend of $10 yesterday, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##10(1+0.05)^1=$10.50## in one year from now, and the year after it will be ##10(1+0.05)^2=11.025## and so on.
The required return of the stock is 15% pa.
For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.
The required return of the stock is 15% pa.
For a price of $10.20 each, Renee will sell you 100 shares. Each share is expected to pay dividends in perpetuity, growing at a rate of 5% pa. The next dividend is one year away (t=1) and is expected to be $1 per share.
The required return of the stock is 15% pa.
For a price of $129, Joanne will sell you a share which is expected to pay a $30 dividend in one year, and a $10 dividend every year after that forever. So the stock's dividends will be $30 at t=1, $10 at t=2, $10 at t=3, and $10 forever onwards.
The required return of the stock is 10% pa.
For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.
The required return of the stock is 10% pa.
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_{0} = \frac{c_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What is the discount rate '## r_\text{eff} ##' in this equation?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
The following is the Dividend Discount Model (DDM) used to price stocks:
### P_0 = \frac{d_1}{r-g} ###Assume that the assumptions of the DDM hold and that the time period is measured in years.
Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.
Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in four and a half years (t = 4.5)?
When using the dividend discount model to price a stock:
### p_{0} = \frac{d_1}{r - g} ###
The growth rate of dividends (g):
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_0 = \frac{d_1}{r - g} ###
Which expression is NOT equal to the expected dividend yield?
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock is 10% pa, given as an effective annual rate.
What is the price of the share now?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###p_0=\frac{d_1}{r_\text{eff}-g_\text{eff}}###
Which expression is NOT equal to the expected capital return?
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.
What is the price of the share now?
A stock pays annual dividends. It just paid a dividend of $3. The growth rate in the dividend is 4% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 8 | 8 | 8 | 20 | 8 | ... |
After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. Note that the $8 dividend at time zero is about to be paid tonight.
What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 8 | 8 | 8 | 20 | 8 | ... |
After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. Note that the $8 dividend at time zero is about to be paid tonight.
What will be the price of the stock in 5 years (t = 5), just after the dividend at that time has been paid?
The following is the Dividend Discount Model used to price stocks:
### p_0=\frac{d_1}{r-g} ###
Which of the following statements about the Dividend Discount Model is NOT correct?
A stock pays annual dividends. It just paid a dividend of $5. The growth rate in the dividend is 1% pa. You estimate that the stock's required return is 8% pa. Both the discount rate and growth rate are given as effective annual rates.
Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 2 | 2 | 2 | 10 | 3 | ... |
After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 2 | 2 | 2 | 10 | 3 | ... |
After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in 5 years (t = 5), just after the dividend at that time has been paid?
Here's the Dividend Discount Model, used to price stocks:
### p_0=\frac{d_1}{r-g} ###
All rates are effective annual rates and the cash flows (##d_1##) are received every year. Note that the r and g terms in the above DDM could also be labelled: ###r = r_{\text{total, 0}\rightarrow\text{1yr, eff 1yr}}### ###g = r_{\text{capital, 0}\rightarrow\text{1yr, eff 1yr}}### Which of the following statements is NOT correct?
A share pays annual dividends. It just paid a dividend of $2. The growth rate in the dividend is 3% pa. You estimate that the stock's required return is 8% pa. Both the discount rate and growth rate are given as effective annual rates.
Using the dividend discount model, what is the share price?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
In the dividend discount model:
###P_0 = \dfrac{C_1}{r-g}###
The return ##r## is supposed to be the:
In the dividend discount model:
### P_0= \frac{d_1}{r-g} ###
The pronumeral ##g## is supposed to be the:
Two years ago Fred bought a house for $300,000.
Now it's worth $500,000, based on recent similar sales in the area.
Fred's residential property has an expected total return of 8% pa.
He rents his house out for $2,000 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $23,173.86.
The future value of 12 months of rental payments one year ahead is $25,027.77.
What is the expected annual growth rate of the rental payments? In other words, by what percentage increase will Fred have to raise the monthly rent by each year to sustain the expected annual total return of 8%?
Stocks in the United States usually pay quarterly dividends. For example, the software giant Microsoft paid a $0.23 dividend every quarter over the 2013 financial year and plans to pay a $0.28 dividend every quarter over the 2014 financial year.
Using the dividend discount model and net present value techniques, calculate the stock price of Microsoft assuming that:
- The time now is the beginning of July 2014. The next dividend of $0.28 will be received in 3 months (end of September 2014), with another 3 quarterly payments of $0.28 after this (end of December 2014, March 2015 and June 2015).
- The quarterly dividend will increase by 2.5% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in the financial year beginning in September 2015 will be $ 0.287 ##(=0.28×(1+0.025)^1)##, with the last at the end of June 2016. In the next financial year beginning in September 2016 each quarterly dividend will be $0.294175 ##(=0.28×(1+0.025)^2)##, with the last at the end of June 2017, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
Question 210 real estate, inflation, real and nominal returns and cash flows, income and capital returns
Assume that the Gordon Growth Model (same as the dividend discount model or perpetuity with growth formula) is an appropriate method to value real estate.
An old rule of thumb in the real estate industry is that properties should yield a 5% pa rental return. Some investors also regard property to be as risky as the stock market, therefore property is thought to have a required total return of 9% pa which is the average total return on the stock market including dividends.
Assume that all returns are effective annual rates and they are nominal (not reduced by inflation). Inflation is expected to be 2% pa.
You're considering purchasing an investment property which has a rental yield of 5% pa and you expect it to have the same risk as the stock market. Select the most correct statement about this property.
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 295 inflation, real and nominal returns and cash flows, NPV
When valuing assets using discounted cash flow (net present value) methods, it is important to consider inflation. To properly deal with inflation:
(I) Discount nominal cash flows by nominal discount rates.
(II) Discount nominal cash flows by real discount rates.
(III) Discount real cash flows by nominal discount rates.
(IV) Discount real cash flows by real discount rates.
Which of the above statements is or are correct?
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 22 NPV, perpetuity with growth, effective rate, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 10% given as an effective annual rate?
The first payment of $90 is in 3 years, followed by payments every 6 months in perpetuity after that which shrink by 3% every 6 months. That is, the growth rate every 6 months is actually negative 3%, given as an effective 6 month rate. So the payment at ## t=3.5 ## years will be ## 90(1-0.03)^1=87.3 ##, and so on.
Due to floods overseas, there is a cut in the supply of the mineral iron ore and its price increases dramatically. An Australian iron ore mining company therefore expects a large but temporary increase in its profit and cash flows. The mining company does not have any positive NPV projects to begin, so what should it do? Select the most correct answer.
Jan asks you for a loan. He wants $100 now and offers to pay you back $120 in 1 year. You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate.
Ignore credit risk. Remember:
### V_0 = \frac{V_t}{(1+r_\text{eff})^t} ###
Katya offers to pay you $10 at the end of every year for the next 5 years (t=1,2,3,4,5) if you pay her $50 now (t=0). You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate. Ignore credit risk.
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
You're advising your superstar client 40-cent who is weighing up buying a private jet or a luxury yacht. 40-cent is just as happy with either, but he wants to go with the more cost-effective option. These are the cash flows of the two options:
- The private jet can be bought for $6m now, which will cost $12,000 per month in fuel, piloting and airport costs, payable at the end of each month. The jet will last for 12 years.
- Or the luxury yacht can be bought for $4m now, which will cost $20,000 per month in fuel, crew and berthing costs, payable at the end of each month. The yacht will last for 20 years.
What's unusual about 40-cent is that he is so famous that he will actually be able to sell his jet or yacht for the same price as it was bought since the next generation of superstar musicians will buy it from him as a status symbol.
Bank interest rates are 10% pa, given as an effective annual rate. You can assume that 40-cent will live for another 60 years and that when the jet or yacht's life is at an end, he will buy a new one with the same details as above.
Would you advise 40-cent to buy the or the ?
Note that the effective monthly rate is ##r_\text{eff monthly}=(1+0.1)^{1/12}-1=0.00797414##
Carlos and Edwin are brothers and they both love Holden Commodore cars.
Carlos likes to buy the latest Holden Commodore car for $40,000 every 4 years as soon as the new model is released. As soon as he buys the new car, he sells the old one on the second hand car market for $20,000. Carlos never has to bother with paying for repairs since his cars are brand new.
Edwin also likes Commodores, but prefers to buy 4-year old cars for $20,000 and keep them for 11 years until the end of their life (new ones last for 15 years in total but the 4-year old ones only last for another 11 years). Then he sells the old car for $2,000 and buys another 4-year old second hand car, and so on.
Every time Edwin buys a second hand 4 year old car he immediately has to spend $1,000 on repairs, and then $1,000 every year after that for the next 10 years. So there are 11 payments in total from when the second hand car is bought at t=0 to the last payment at t=10. One year later (t=11) the old car is at the end of its total 15 year life and can be scrapped for $2,000.
Assuming that Carlos and Edwin maintain their love of Commodores and keep up their habits of buying new ones and second hand ones respectively, how much larger is Carlos' equivalent annual cost of car ownership compared with Edwin's?
The real discount rate is 10% pa. All cash flows are real and are expected to remain constant. Inflation is forecast to be 3% pa. All rates are effective annual. Ignore capital gains tax and tax savings from depreciation since cars are tax-exempt for individuals.
You just bought a nice dress which you plan to wear once per month on nights out. You bought it a moment ago for $600 (at t=0). In your experience, dresses used once per month last for 6 years.
Your younger sister is a student with no money and wants to borrow your dress once a month when she hits the town. With the increased use, your dress will only last for another 3 years rather than 6.
What is the present value of the cost of letting your sister use your current dress for the next 3 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new dress when your current one wears out; your sister will only use the current dress, not the next one that you will buy; and the price of a new dress never changes.
Question 207 income and capital returns, bond pricing, coupon rate, no explanation
For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?
Let: ##P_0## be the bond price now,
##F_T## be the bond's face value,
##T## be the bond's maturity in years,
##r_\text{total}## be the bond's total yield,
##r_\text{income}## be the bond's income yield,
##r_\text{capital}## be the bond's capital yield, and
##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.
Your credit card shows a $600 debt liability. The interest rate is 24% pa, payable monthly. You can't pay any of the debt off, except in 6 months when it's your birthday and you'll receive $50 which you'll use to pay off the credit card. If that is your only repayment, how much will the credit card debt liability be one year from now?
Question 25 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 2 year zero coupon bond at a yield of 8% pa, and a
- 3 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 96 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds paying semi-annual coupons:
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 108 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 1 year zero coupon bond at a yield of 10% pa, and
- A 2 year zero coupon bond at a yield of 8% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 143 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 6-month zero coupon bond at a yield of 6% pa, and
- A 12 month zero coupon bond at a yield of 7% pa.
What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
A European company just issued two bonds, a
- 3 year zero coupon bond at a yield of 6% pa, and a
- 4 year zero coupon bond at a yield of 6.5% pa.
What is the company's forward rate over the fourth year (from t=3 to t=4)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
A 180-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A 90-day Bank Accepted Bill (BAB) has a face value of $1,000,000. The simple interest rate is 10% pa and there are 365 days in the year. What is its price now?
Question 147 bill pricing, simple interest rate, no explanation
A 30-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
Question 157 bill pricing, simple interest rate, no explanation
A 90-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 6% pa and there are 365 days in the year. What is its price?
A 60-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
Question 327 bill pricing, simple interest rate, no explanation
On 27/09/13, three month Swiss government bills traded at a yield of -0.2%, given as a simple annual yield. That is, interest rates were negative.
If the face value of one of these 90 day bills is CHF1,000,000 (CHF represents Swiss Francs, the Swiss currency), what is the price of one of these bills?
Below are 4 option graphs. Note that the y-axis is payoff at maturity (T). What options do they depict? List them in the order that they are numbered.
Which one of the following is NOT usually considered an 'investable' asset for long-term wealth creation?
You believe that the price of a share will fall significantly very soon, but the rest of the market does not. The market thinks that the share price will remain the same. Assuming that your prediction will soon be true, which of the following trades is a bad idea? In other words, which trade will NOT make money or prevent losses?
Question 382 Merton model of corporate debt, real option, option
In the Merton model of corporate debt, buying a levered company's shares is equivalent to:
Question 385 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The levered equity graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?
Question 383 Merton model of corporate debt, real option, option
In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying the company's assets and:
Which of the following is the least useful method or model to calculate the value of a real option in a project?
Question 386 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The risky corporate debt graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?
One of the reasons why firms may not begin projects with relatively small positive net present values (NPV's) is because they wish to maximise the value of their:
A moped is a bicycle with pedals and a little motor that can be switched on to assist the rider. Mopeds are useful for quick transport using the motor, and for physical exercise when using the pedals unassisted. This offers the rider:
You're thinking of starting a new cafe business, but you're not sure if it will be profitable.
You have to decide what type of cups, mugs and glasses you wish to buy. You can pay to have your cafe's name printed on them, or just buy the plain un-marked ones. For marketing reasons it's better to have the cafe name printed. But the plain un-marked cups, mugs and glasses maximise your:
Some financially minded people insist on a prenuptial agreement before committing to marry their partner. This agreement states how the couple's assets should be divided in case they divorce. Prenuptial agreements are designed to give the richer partner more of the couples' assets if they divorce, thus maximising the richer partner's:
The cheapest mobile phones available tend to be those that are 'locked' into a cell phone operator's network. Locked phones can not be used with other cell phone operators' networks.
Locked mobile phones are cheaper than unlocked phones because the locked-in network operator helps create a monopoly by:
Your firm's research scientists can begin an exciting new project at a cost of $10m now, after which there’s a:
- 70% chance that cash flows will be $1m per year forever, starting in 5 years (t=5). This is the A state of the world.
- 20% chance that cash flows will be $3m per year forever, starting in 5 years (t=5). This is the B state of the world.
- 10% chance of a major break through in which case the cash flows will be $20m per year forever starting in 5 years (t=5), or instead, the project can be expanded by investing another $10m (at t=5) which is expected to give cash flows of $60m per year forever, starting at year 9 (t=9). Note that the perpetual cash flows are either the $20m from year 4 onwards, or the $60m from year 9 onwards after the additional $10m year 5 investment, but not both. This is the C state of the world.
The firm's cost of capital is 10% pa.
What's the present value (at t=0) of the option to expand in year 5?
Acquirer firm plans to launch a takeover of Target firm. The deal is expected to create a present value of synergies totaling $105 million. A cash offer will be made that pays the fair price for the target's shares plus 75% of the total synergy value. The cash will be paid out of the firm's cash holdings, no new debt or equity will be raised.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 6,000 | 700 |
| Debt ($m) | 4,800 | 400 |
| Share price ($) | 40 | 20 |
| Number of shares (m) | 30 | 15 |
Ignore transaction costs and fees. Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.
Acquirer firm plans to launch a takeover of Target firm. The deal is expected to create a present value of synergies totaling $105 million. A scrip offer will be made that pays the fair price for the target's shares plus 75% of the total synergy value.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 6,000 | 700 |
| Debt ($m) | 4,800 | 400 |
| Share price ($) | 40 | 20 |
| Number of shares (m) | 30 | 15 |
Ignore transaction costs and fees. Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.
Acquirer firm plans to launch a takeover of Target firm. The firms operate in different industries and the CEO's rationale for the merger is to increase diversification and thereby decrease risk. The deal is not expected to create any synergies. An 80% scrip and 20% cash offer will be made that pays the fair price for the target's shares. The cash will be paid out of the firms' cash holdings, no new debt or equity will be raised.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 6,000 | 700 |
| Debt ($m) | 4,800 | 400 |
| Share price ($) | 40 | 20 |
| Number of shares (m) | 30 | 15 |
Ignore transaction costs and fees. Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.
Acquirer firm plans to launch a takeover of Target firm. The deal is expected to create a present value of synergies totaling $105 million. A 40% scrip and 60% cash offer will be made that pays the fair price for the target's shares plus 75% of the total synergy value. The cash will be paid out of the firm's cash holdings, no new debt or equity will be raised.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 6,000 | 700 |
| Debt ($m) | 4,800 | 400 |
| Share price ($) | 40 | 20 |
| Number of shares (m) | 30 | 15 |
Ignore transaction costs and fees. Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.
Acquirer firm plans to launch a takeover of Target firm. The deal is expected to create a present value of synergies totaling $2 million. A cash offer will be made that pays the fair price for the target's shares plus 70% of the total synergy value. The cash will be paid out of the firm's cash holdings, no new debt or equity will be raised.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 60 | 10 |
| Debt ($m) | 20 | 2 |
| Share price ($) | 10 | 8 |
| Number of shares (m) | 4 | 1 |
Ignore transaction costs and fees. Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.
Acquirer firm plans to launch a takeover of Target firm. The deal is expected to create a present value of synergies totaling $2 million. A scrip offer will be made that pays the fair price for the target's shares plus 70% of the total synergy value.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 60 | 10 |
| Debt ($m) | 20 | 2 |
| Share price ($) | 10 | 8 |
| Number of shares (m) | 4 | 1 |
Ignore transaction costs and fees. Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.
Acquirer firm plans to launch a takeover of Target firm. The deal is expected to create a present value of synergies totaling $0.5 million, but investment bank fees and integration costs with a present value of $1.5 million is expected. A 10% cash and 90% scrip offer will be made that pays the fair price for the target's shares only. Assume that the Target and Acquirer agree to the deal. The cash will be paid out of the firms' cash holdings, no new debt or equity will be raised.
| Firms Involved in the Takeover | ||
| Acquirer | Target | |
| Assets ($m) | 60 | 10 |
| Debt ($m) | 20 | 2 |
| Share price ($) | 10 | 8 |
| Number of shares (m) | 4 | 1 |
Assume that the firms' debt and equity are fairly priced, and that each firms' debts' risk, yield and values remain constant. The acquisition is planned to occur immediately, so ignore the time value of money.
Calculate the merged firm's share price and total number of shares after the takeover has been completed.