If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
What is the payback period of the project in years?
Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $500 at time 2 is actually earned smoothly from t=1 to t=2.
A project to build a toll road will take 3 years to complete, costing three payments of $50 million, paid at the start of each year (at times 0, 1, and 2).
After completion, the toll road will yield a constant $10 million at the end of each year forever with no costs. So the first payment will be at t=4.
The required return of the project is 10% pa given as an effective nominal rate. All cash flows are nominal.
What is the payback period?
You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.
How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.
Your main expense is fuel for your car which costs $100 per month. You just refueled, so you won't need any more fuel for another month (first payment at t=1 month).
You have $2,500 in a bank account which pays interest at a rate of 6% pa, payable monthly. Interest rates are not expected to change.
Assuming that you have no income, in how many months time will you not have enough money to fully refuel your car?
You really want to go on a back packing trip to Europe when you finish university. Currently you have $1,500 in the bank. Bank interest rates are 8% pa, given as an APR compounding per month. If the holiday will cost $2,000, how long will it take for your bank account to reach that amount?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
To your surprise, you can actually afford to pay $2,000 per month and your mortgage allows early repayments without fees. If you maintain these higher monthly payments, how long will it take to pay off your mortgage?
You're trying to save enough money for a deposit to buy a house. You want to buy a house worth $400,000 and the bank requires a 20% deposit ($80,000) before it will give you a loan for the other $320,000 that you need.
You currently have no savings, but you just started working and can save $2,000 per month, with the first payment in one month from now. Bank interest rates on savings accounts are 4.8% pa with interest paid monthly and interest rates are not expected to change.
How long will it take to save the $80,000 deposit? Round your answer up to the nearest month.
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
The below graph shows a project's net present value (NPV) against its annual discount rate.
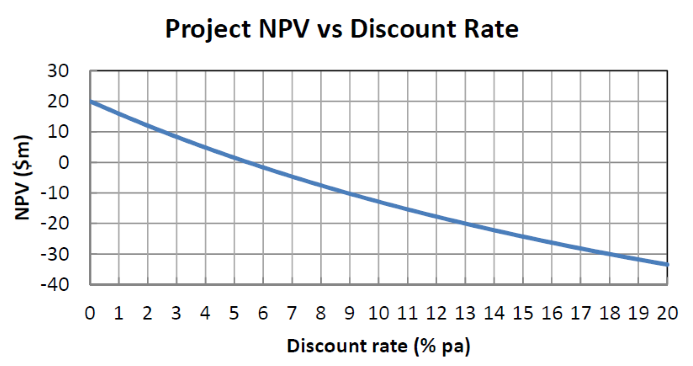
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
The below graph shows a project's net present value (NPV) against its annual discount rate.

Which of the following statements is NOT correct?
A firm is considering a business project which costs $11m now and is expected to pay a constant $1m at the end of every year forever.
Assume that the initial $11m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
Question 579 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to double if the price grows by 10% pa?
Question 580 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to quadruple (be four times as big, say from $1 to $4) if the price grows by 15% pa?
The saying "buy low, sell high" suggests that investors should make a:
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
Total cash flows can be broken into income and capital cash flows. What is the name given to the income cash flow from owning shares?
Which of the following equations is NOT equal to the total return of an asset?
Let ##p_0## be the current price, ##p_1## the expected price in one year and ##c_1## the expected income in one year.
An asset's total expected return over the next year is given by:
###r_\text{total} = \dfrac{c_1+p_1-p_0}{p_0} ###
Where ##p_0## is the current price, ##c_1## is the expected income in one year and ##p_1## is the expected price in one year. The total return can be split into the income return and the capital return.
Which of the following is the expected capital return?
A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).
What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
A share was bought for $30 (at t=0) and paid its annual dividend of $6 one year later (at t=1).
Just after the dividend was paid, the share price fell to $27 (at t=1). What were the total, capital and income returns given as effective annual rates?
The choices are given in the same order:
##r_\text{total}## , ##r_\text{capital}## , ##r_\text{dividend}##.
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
One and a half years ago Frank bought a house for $600,000. Now it's worth only $500,000, based on recent similar sales in the area.
The expected total return on Frank's residential property is 7% pa.
He rents his house out for $1,600 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $18,617.27.
The future value of 12 months of rental payments one year in the future is $19,920.48.
What is the expected annual rental yield of the property? Ignore the costs of renting such as maintenance, real estate agent fees and so on.
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 295 inflation, real and nominal returns and cash flows, NPV
When valuing assets using discounted cash flow (net present value) methods, it is important to consider inflation. To properly deal with inflation:
(I) Discount nominal cash flows by nominal discount rates.
(II) Discount nominal cash flows by real discount rates.
(III) Discount real cash flows by nominal discount rates.
(IV) Discount real cash flows by real discount rates.
Which of the above statements is or are correct?
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 363 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 8% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.
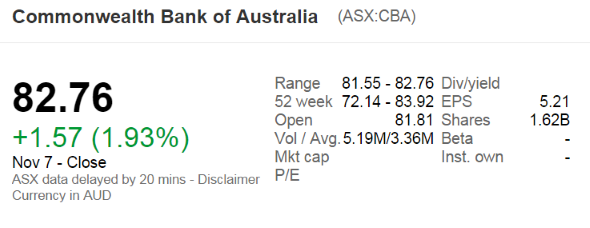
What was CBA's market capitalisation of equity?
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.
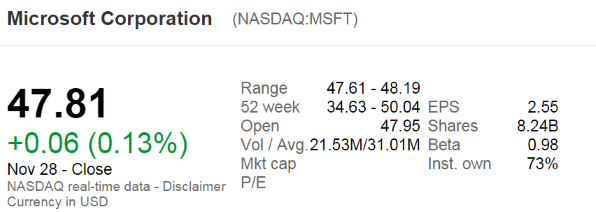
What was MSFT's market capitalisation of equity?
Which of the following statements about book and market equity is NOT correct?
Question 444 investment decision, corporate financial decision theory
The investment decision primarily affects which part of a business?
Question 446 working capital decision, corporate financial decision theory
The working capital decision primarily affects which part of a business?
Question 445 financing decision, corporate financial decision theory
The financing decision primarily affects which part of a business?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
Question 443 corporate financial decision theory, investment decision, financing decision, working capital decision, payout policy
Business people make lots of important decisions. Which of the following is the most important long term decision?
You're considering making an investment in a particular company. They have preference shares, ordinary shares, senior debt and junior debt.
Which is the safest investment? Which has the highest expected returns?
A newly floated farming company is financed with senior bonds, junior bonds, cumulative non-voting preferred stock and common stock. The new company has no retained profits and due to floods it was unable to record any revenues this year, leading to a loss. The firm is not bankrupt yet since it still has substantial contributed equity (same as paid-up capital).
On which securities must it pay interest or dividend payments in this terrible financial year?
Which business structure or structures have the advantage of limited liability for equity investors?
Question 452 limited liability, expected and historical returns
What is the lowest and highest expected share price and expected return from owning shares in a company over a finite period of time?
Let the current share price be ##p_0##, the expected future share price be ##p_1##, the expected future dividend be ##d_1## and the expected return be ##r##. Define the expected return as:
##r=\dfrac{p_1-p_0+d_1}{p_0} ##
The answer choices are stated using inequalities. As an example, the first answer choice "(a) ##0≤p<∞## and ##0≤r< 1##", states that the share price must be larger than or equal to zero and less than positive infinity, and that the return must be larger than or equal to zero and less than one.
Question 542 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to double every 10 years, what must be the expected future capital return, given as an effective annual rate?
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 526 real and nominal returns and cash flows, inflation, no explanation
How can a nominal cash flow be precisely converted into a real cash flow?
Question 577 inflation, real and nominal returns and cash flows
What is the present value of a real payment of $500 in 2 years? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
The expression 'you have to spend money to make money' relates to which business decision?
Katya offers to pay you $10 at the end of every year for the next 5 years (t=1,2,3,4,5) if you pay her $50 now (t=0). You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate. Ignore credit risk.
There are many ways to write the ordinary annuity formula.
Which of the following is NOT equal to the ordinary annuity formula?
The following cash flows are expected:
- 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
- 1 payment of $400 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.
What is the net present value (NPV) of borrowing from your friend?
Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
Some countries' interest rates are so low that they're zero.
If interest rates are 0% pa and are expected to stay at that level for the foreseeable future, what is the most that you would be prepared to pay a bank now if it offered to pay you $10 at the end of every year for the next 5 years?
In other words, what is the present value of five $10 payments at time 1, 2, 3, 4 and 5 if interest rates are 0% pa?
Discounted cash flow (DCF) valuation prices assets by finding the present value of the asset's future cash flows. The single cash flow, annuity, and perpetuity equations are very useful for this.
Which of the following equations is the 'perpetuity with growth' equation?
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
The first payment of a constant perpetual annual cash flow is received at time 5. Let this cash flow be ##C_5## and the required return be ##r##.
So there will be equal annual cash flows at time 5, 6, 7 and so on forever, and all of the cash flows will be equal so ##C_5 = C_6 = C_7 = ...##
When the perpetuity formula is used to value this stream of cash flows, it will give a value (V) at time:
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.
What is the implied growth rate of the dividend per year?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
In the dividend discount model:
###P_0 = \dfrac{C_1}{r-g}###
The return ##r## is supposed to be the:
Two years ago Fred bought a house for $300,000.
Now it's worth $500,000, based on recent similar sales in the area.
Fred's residential property has an expected total return of 8% pa.
He rents his house out for $2,000 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $23,173.86.
The future value of 12 months of rental payments one year ahead is $25,027.77.
What is the expected annual growth rate of the rental payments? In other words, by what percentage increase will Fred have to raise the monthly rent by each year to sustain the expected annual total return of 8%?
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.
What is the price of the share now?
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
The following is the Dividend Discount Model (DDM) used to price stocks:
### P_0 = \frac{d_1}{r-g} ###Assume that the assumptions of the DDM hold and that the time period is measured in years.
Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_0 = \frac{d_1}{r - g} ###
Which expression is NOT equal to the expected dividend yield?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###p_0=\frac{d_1}{r_\text{eff}-g_\text{eff}}###
Which expression is NOT equal to the expected capital return?
A fairly valued share's current price is $4 and it has a total required return of 30%. Dividends are paid annually and next year's dividend is expected to be $1. After that, dividends are expected to grow by 5% pa in perpetuity. All rates are effective annual returns.
What is the expected dividend income paid at the end of the second year (t=2) and what is the expected capital gain from just after the first dividend (t=1) to just after the second dividend (t=2)? The answers are given in the same order, the dividend and then the capital gain.
A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.
Using the dividend discount model, what will be the share price?
Question 488 income and capital returns, payout policy, payout ratio, DDM
Two companies BigDiv and ZeroDiv are exactly the same except for their dividend payouts.
BigDiv pays large dividends and ZeroDiv doesn't pay any dividends.
Currently the two firms have the same earnings, assets, number of shares, share price, expected total return and risk.
Assume a perfect world with no taxes, no transaction costs, no asymmetric information and that all assets including business projects are fairly priced and therefore zero-NPV.
All things remaining equal, which of the following statements is NOT correct?
Question 498 NPV, Annuity, perpetuity with growth, multi stage growth model
A business project is expected to cost $100 now (t=0), then pay $10 at the end of the third (t=3), fourth, fifth and sixth years, and then grow by 5% pa every year forever. So the cash flow will be $10.5 at the end of the seventh year (t=7), then $11.025 at the end of the eighth year (t=8) and so on perpetually. The total required return is 10℅ pa.
Which of the following formulas will NOT give the correct net present value of the project?
A low-quality second-hand car can be bought now for $1,000 and will last for 1 year before it will be scrapped for nothing.
A high-quality second-hand car can be bought now for $4,900 and it will last for 5 years before it will be scrapped for nothing.
What is the equivalent annual cost of each car? Assume a discount rate of 10% pa, given as an effective annual rate.
The answer choices are given as the equivalent annual cost of the low-quality car and then the high quality car.
Question 180 equivalent annual cash flow, inflation, real and nominal returns and cash flows
Details of two different types of light bulbs are given below:
- Low-energy light bulbs cost $3.50, have a life of nine years, and use about $1.60 of electricity a year, paid at the end of each year.
- Conventional light bulbs cost only $0.50, but last only about a year and use about $6.60 of energy a year, paid at the end of each year.
The real discount rate is 5%, given as an effective annual rate. Assume that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the Equivalent Annual Cost (EAC) of the low-energy and conventional light bulbs. The below choices are listed in that order.
You're advising your superstar client 40-cent who is weighing up buying a private jet or a luxury yacht. 40-cent is just as happy with either, but he wants to go with the more cost-effective option. These are the cash flows of the two options:
- The private jet can be bought for $6m now, which will cost $12,000 per month in fuel, piloting and airport costs, payable at the end of each month. The jet will last for 12 years.
- Or the luxury yacht can be bought for $4m now, which will cost $20,000 per month in fuel, crew and berthing costs, payable at the end of each month. The yacht will last for 20 years.
What's unusual about 40-cent is that he is so famous that he will actually be able to sell his jet or yacht for the same price as it was bought since the next generation of superstar musicians will buy it from him as a status symbol.
Bank interest rates are 10% pa, given as an effective annual rate. You can assume that 40-cent will live for another 60 years and that when the jet or yacht's life is at an end, he will buy a new one with the same details as above.
Would you advise 40-cent to buy the or the ?
Note that the effective monthly rate is ##r_\text{eff monthly}=(1+0.1)^{1/12}-1=0.00797414##
Question 215 equivalent annual cash flow, effective rate conversion
You're about to buy a car. These are the cash flows of the two different cars that you can buy:
- You can buy an old car for $5,000 now, for which you will have to buy $90 of fuel at the end of each week from the date of purchase. The old car will last for 3 years, at which point you will sell the old car for $500.
- Or you can buy a new car for $14,000 now for which you will have to buy $50 of fuel at the end of each week from the date of purchase. The new car will last for 4 years, at which point you will sell the new car for $1,000.
Bank interest rates are 10% pa, given as an effective annual rate. Assume that there are exactly 52 weeks in a year. Ignore taxes and environmental and pollution factors.
Should you buy the or the ?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
Question 64 inflation, real and nominal returns and cash flows, APR, effective rate
In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.
The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
Which of the following statements is NOT equivalent to the yield on debt?
Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just agreed to a 30 year fully amortising mortgage loan with monthly payments of $2,500. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change. The below choices are given in the same order.
You want to buy a house priced at $400,000. You have saved a deposit of $40,000. The bank has agreed to lend you $360,000 as a fully amortising loan with a term of 30 years. The interest rate is 8% pa payable monthly and is not expected to change.
What will be your monthly payments?
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
You want to buy an apartment worth $300,000. You have saved a deposit of $60,000.
The bank has agreed to lend you $240,000 as an interest only mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
A prospective home buyer can afford to pay $2,000 per month in mortgage loan repayments. The central bank recently lowered its policy rate by 0.25%, and residential home lenders cut their mortgage loan rates from 4.74% to 4.49%.
How much more can the prospective home buyer borrow now that interest rates are 4.49% rather than 4.74%? Give your answer as a proportional increase over the original amount he could borrow (##V_\text{before}##), so:
###\text{Proportional increase} = \frac{V_\text{after}-V_\text{before}}{V_\text{before}} ###Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates compounding per month.
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid annually. So there's only one coupon per year, paid in arrears every year.
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid semi-annually. So there are two coupons per year, paid in arrears every six months.
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
Question 48 IRR, NPV, bond pricing, premium par and discount bonds, market efficiency
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A two year Government bond has a face value of $100, a yield of 2.5% pa and a fixed coupon rate of 0.5% pa, paid semi-annually. What is its price?
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?
Bonds A and B are issued by the same Australian company. Both bonds yield 7% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond A pays coupons of 10% pa and bond B pays coupons of 5% pa. Which of the following statements is true about the bonds' prices?
Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100) and maturity (3 years).
The only difference is that bond X and Y's yields are 8 and 12% pa respectively. Which of the following statements is true?
A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?
Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100), maturity (3 years) and yield (10%) as each other.
Which of the following statements is true?
A four year bond has a face value of $100, a yield of 6% and a fixed coupon rate of 12%, paid semi-annually. What is its price?
Which one of the following bonds is trading at a discount?
A firm wishes to raise $20 million now. They will issue 8% pa semi-annual coupon bonds that will mature in 5 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
A five year bond has a face value of $100, a yield of 12% and a fixed coupon rate of 6%, paid semi-annually.
What is the bond's price?
Which one of the following bonds is trading at par?
A firm wishes to raise $8 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
Which one of the following bonds is trading at a premium?
A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 8 years and have a face value of $1,000 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue? All numbers are rounded up.
A four year bond has a face value of $100, a yield of 9% and a fixed coupon rate of 6%, paid semi-annually. What is its price?
A 10 year bond has a face value of $100, a yield of 6% pa and a fixed coupon rate of 8% pa, paid semi-annually. What is its price?
A 30 year Japanese government bond was just issued at par with a yield of 1.7% pa. The fixed coupon payments are semi-annual. The bond has a face value of $100.
Six months later, just after the first coupon is paid, the yield of the bond increases to 2% pa. What is the bond's new price?
A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.
Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?
Bonds X and Y are issued by the same US company. Both bonds yield 6% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X pays coupons of 8% pa and bond Y pays coupons of 12% pa. Which of the following statements is true?
Below are some statements about loans and bonds. The first descriptive sentence is correct. But one of the second sentences about the loans' or bonds' prices is not correct. Which statement is NOT correct? Assume that interest rates are positive.
Note that coupons or interest payments are the periodic payments made throughout a bond or loan's life. The face or par value of a bond or loan is the amount paid at the end when the debt matures.
A home loan company advertises an interest rate of 6% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 96 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds paying semi-annual coupons:
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 3 years from now (first payment at t=3).
- 1 payment of $600 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 727 inflation, real and nominal returns and cash flows
The Australian Federal Government lends money to domestic students to pay for their university education. This is known as the Higher Education Contribution Scheme (HECS). The nominal interest rate on the HECS loan is set equal to the consumer price index (CPI) inflation rate. The interest is capitalised every year, which means that the interest is added to the principal. The interest and principal does not need to be repaid by students until they finish study and begin working.
Which of the following statements about HECS loans is NOT correct?
Question 729 book and market values, balance sheet, no explanation
If a firm makes a profit and pays no dividends, which of the firm’s accounts will increase?
In the dividend discount model (DDM), share prices fall when dividends are paid. Let the high price before the fall be called the peak, and the low price after the fall be called the trough.
###P_0=\dfrac{C_1}{r-g}###
Which of the following statements about the DDM is NOT correct?
A share currently worth $100 is expected to pay a constant dividend of $4 for the next 5 years with the first dividend in one year (t=1) and the last in 5 years (t=5).
The total required return is 10% pa.
What do you expected the share price to be in 5 years, just after the dividend at that time has been paid?
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Find Ching-A-Lings Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Ching-A-Lings Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 20 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 30 | |
| Taxes at 30% | 9 | |
| Net income | 21 | |
| Ching-A-Lings Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 49 | 38 |
| Trade debtors | 14 | 2 |
| Rent paid in advance | 5 | 5 |
| PPE | 400 | 400 |
| Total assets | 468 | 445 |
| Trade creditors | 4 | 10 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 145 | 145 |
| Retained profits | 119 | 100 |
| Total L and OE | 468 | 445 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
- Pay dividends of $1m.
- Complete a $1.3m share buy-back.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Read the following financial statements and calculate the firm's free cash flow over the 2014 financial year.
| UBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2014 | ||
| $m | ||
| Sales | 293 | |
| COGS | 200 | |
| Rent expense | 15 | |
| Gas expense | 8 | |
| Depreciation | 10 | |
| EBIT | 60 | |
| Interest expense | 0 | |
| Taxable income | 60 | |
| Taxes | 18 | |
| Net income | 42 | |
| UBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2014 | 2013 |
| $m | $m | |
| Assets | ||
| Cash | 30 | 29 |
| Accounts receivable | 5 | 7 |
| Pre-paid rent expense | 1 | 0 |
| Inventory | 50 | 46 |
| PPE | 290 | 300 |
| Total assets | 376 | 382 |
| Liabilities | ||
| Trade payables | 20 | 18 |
| Accrued gas expense | 3 | 2 |
| Non-current liabilities | 0 | 0 |
| Contributed equity | 212 | 212 |
| Retained profits | 136 | 150 |
| Asset revaluation reserve | 5 | 0 |
| Total L and OE | 376 | 382 |
Note: all figures are given in millions of dollars ($m).
The firm's free cash flow over the 2014 financial year was:
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| UniBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 80 | |
| COGS | 40 | |
| Operating expense | 15 | |
| Depreciation | 10 | |
| Interest expense | 5 | |
| Income before tax | 10 | |
| Tax at 30% | 3 | |
| Net income | 7 | |
| UniBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 90 |
| PPE | ||
| Cost | 360 | 320 |
| Accumul. depr. | 40 | 30 |
| Carrying amount | 320 | 290 |
| Total assets | 440 | 380 |
| Liabilities | ||
| Current liabilities | 110 | 60 |
| Non-current liabilities | 190 | 180 |
| Owners' equity | ||
| Retained earnings | 95 | 95 |
| Contributed equity | 45 | 45 |
| Total L and OE | 440 | 380 |
Note: all figures are given in millions of dollars ($m).
Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Piano Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 310 | |
| COGS | 185 | |
| Operating expense | 20 | |
| Depreciation | 15 | |
| Interest expense | 10 | |
| Income before tax | 80 | |
| Tax at 30% | 24 | |
| Net income | 56 | |
| Piano Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 240 | 230 |
| PPE | ||
| Cost | 420 | 400 |
| Accumul. depr. | 50 | 35 |
| Carrying amount | 370 | 365 |
| Total assets | 610 | 595 |
| Liabilities | ||
| Current liabilities | 180 | 190 |
| Non-current liabilities | 290 | 265 |
| Owners' equity | ||
| Retained earnings | 90 | 90 |
| Contributed equity | 50 | 50 |
| Total L and OE | 610 | 595 |
Note: all figures are given in millions of dollars ($m).
Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| World Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 300 | |
| COGS | 150 | |
| Operating expense | 50 | |
| Depreciation | 40 | |
| Interest expense | 10 | |
| Taxable income | 50 | |
| Tax at 30% | 15 | |
| Net income | 35 | |
| World Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 200 | 230 |
| PPE | ||
| Cost | 400 | 400 |
| Accumul. depr. | 75 | 35 |
| Carrying amount | 325 | 365 |
| Total assets | 525 | 595 |
| Liabilities | ||
| Current liabilities | 150 | 205 |
| Non-current liabilities | 235 | 250 |
| Owners' equity | ||
| Retained earnings | 100 | 100 |
| Contributed equity | 40 | 40 |
| Total L and OE | 525 | 595 |
Note: all figures above and below are given in millions of dollars ($m).
Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Scubar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 60 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 90 | |
| Taxes at 30% | 27 | |
| Net income | 63 | |
| Scubar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 60 | 50 |
| Trade debtors | 19 | 6 |
| Rent paid in advance | 3 | 2 |
| PPE | 420 | 400 |
| Total assets | 502 | 458 |
| Trade creditors | 10 | 8 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 130 | 130 |
| Retained profits | 162 | 130 |
| Total L and OE | 502 | 458 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
A young lady is trying to decide if she should attend university or not.
The young lady's parents say that she must attend university because otherwise all of her hard work studying and attending school during her childhood was a waste.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The hard work studying at school in her childhood should be classified as:
A young lady is trying to decide if she should attend university. Her friends say that she should go to university because she is more likely to meet a clever young man than if she begins full time work straight away.
What's the correct way to classify this item from a capital budgeting perspective when trying to find the Net Present Value of going to university rather than working?
The opportunity to meet a desirable future spouse should be classified as:
A man is thinking about taking a day off from his casual painting job to relax.
He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.
But he's thinking about the hours that he could work today (in the future) which are:
A man has taken a day off from his casual painting job to relax.
It's the end of the day and he's thinking about the hours that he could have spent working (in the past) which are now:
Find the cash flow from assets (CFFA) of the following project.
| Project Data | ||
| Project life | 2 years | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year for tax purposes | $1m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $3 | |
| Fixed costs per year, paid at the end of each year | $1.5m | |
| Tax rate | 30% | |
Note 1: The equipment will have a book value of $4m at the end of the project for tax purposes. However, the equipment is expected to fetch $0.9 million when it is sold at t=2.
Note 2: Due to the project, the firm will have to purchase $0.8m of inventory initially, which it will sell at t=1. The firm will buy another $0.8m at t=1 and sell it all again at t=2 with zero inventory left. The project will have no effect on the firm's current liabilities.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
Question 99 capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.
Assume that:
- The firm and individual investors can borrow at the same rate and have the same tax rates.
- The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
- There are no market frictions relating to debt such as asymmetric information or transaction costs.
- Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.
According to Miller and Modigliani's theory, which statement is correct?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
Question 559 variance, standard deviation, covariance, correlation
Which of the following statements about standard statistical mathematics notation is NOT correct?
Diversification in a portfolio of two assets works best when the correlation between their returns is:
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
All things remaining equal, the higher the correlation of returns between two stocks:
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 6% pa.
- Stock A has an expected return of 5% pa.
- Stock B has an expected return of 10% pa.
What portfolio weights should the investor have in stocks A and B respectively?
Question 556 portfolio risk, portfolio return, standard deviation
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 12% pa.
- Stock A has an expected return of 10% pa and a standard deviation of 20% pa.
- Stock B has an expected return of 15% pa and a standard deviation of 30% pa.
The correlation coefficient between stock A and B's expected returns is 70%.
What will be the annual standard deviation of the portfolio with this 12% pa target return?
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
Question 703 utility, risk aversion, utility function, gamble
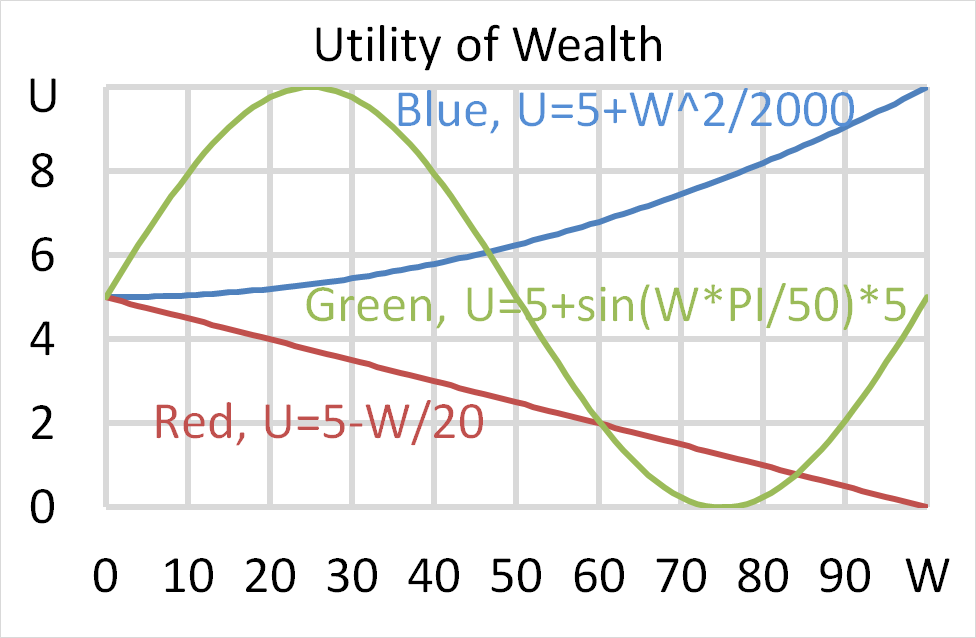
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $500 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $500. Each player can flip a coin and if they flip heads, they receive $500. If they flip tails then they will lose $500. Which of the following statements is NOT correct?
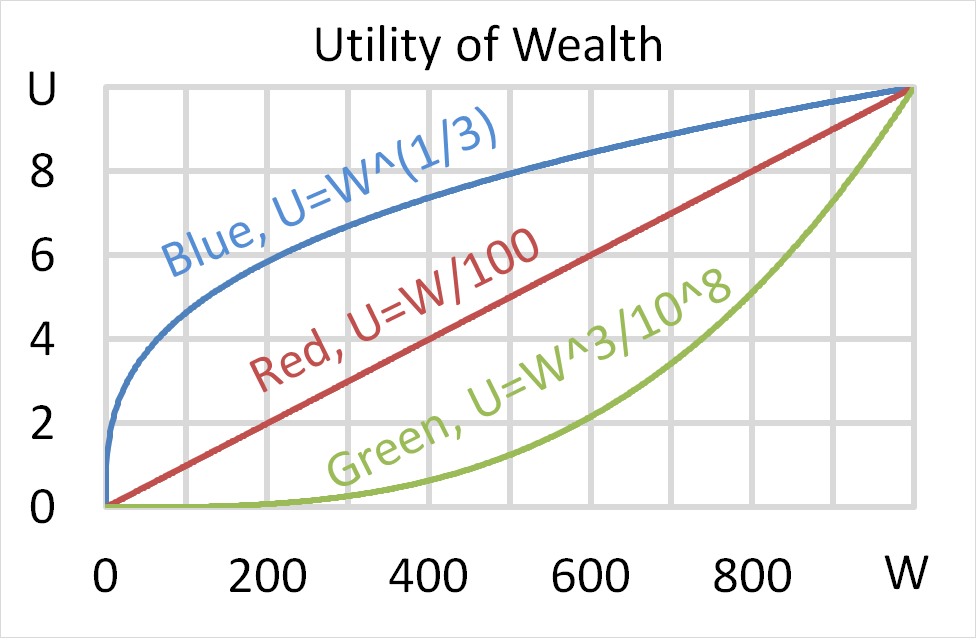
Question 704 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $256 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $256. Each player can flip a coin and if they flip heads, they receive $256. If they flip tails then they will lose $256. Which of the following statements is NOT correct?

Question 702 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
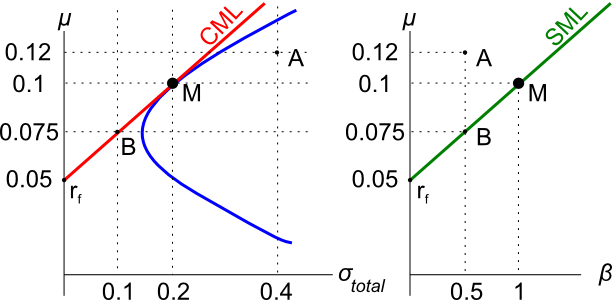
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?

Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
What do you think will be the stock's expected return over the next year, given as an effective annual rate?
Question 418 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $8m | |
| Depreciation of equipment per year | $8m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 4m | |
| Sale price per unit | $10 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense in first year (at t=1) | $0.562m | |
| Corporate tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 9% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.32 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-equity ratio | 50% | |
Notes
- Due to the project, current assets will increase by $6m now (t=0) and fall by $6m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa. All rates are given as effective annual rates.
- The project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Select the most correct statement from the following.
'Chartists', also known as 'technical traders', believe that:
Fundamentalists who analyse company financial reports and news announcements (but who don't have inside information) will make positive abnormal returns if:
Question 100 market efficiency, technical analysis, joint hypothesis problem
A company selling charting and technical analysis software claims that independent academic studies have shown that its software makes significantly positive abnormal returns. Assuming the claim is true, which statement(s) are correct?
(I) Weak form market efficiency is broken.
(II) Semi-strong form market efficiency is broken.
(III) Strong form market efficiency is broken.
(IV) The asset pricing model used to measure the abnormal returns (such as the CAPM) had mis-specification error so the returns may not be abnormal but rather fair for the level of risk.
Select the most correct response:
Question 119 market efficiency, fundamental analysis, joint hypothesis problem
Your friend claims that by reading 'The Economist' magazine's economic news articles, she can identify shares that will have positive abnormal expected returns over the next 2 years. Assuming that her claim is true, which statement(s) are correct?
(i) Weak form market efficiency is broken.
(ii) Semi-strong form market efficiency is broken.
(iii) Strong form market efficiency is broken.
(iv) The asset pricing model used to measure the abnormal returns (such as the CAPM) is either wrong (mis-specification error) or is measured using the wrong inputs (data errors) so the returns may not be abnormal but rather fair for the level of risk.
Select the most correct response:
Question 338 market efficiency, CAPM, opportunity cost, technical analysis
A man inherits $500,000 worth of shares.
He believes that by learning the secrets of trading, keeping up with the financial news and doing complex trend analysis with charts that he can quit his job and become a self-employed day trader in the equities markets.
What is the expected gain from doing this over the first year? Measure the net gain in wealth received at the end of this first year due to the decision to become a day trader. Assume the following:
- He earns $60,000 pa in his current job, paid in a lump sum at the end of each year.
- He enjoys examining share price graphs and day trading just as much as he enjoys his current job.
- Stock markets are weak form and semi-strong form efficient.
- He has no inside information.
- He makes 1 trade every day and there are 250 trading days in the year. Trading costs are $20 per trade. His broker invoices him for the trading costs at the end of the year.
- The shares that he currently owns and the shares that he intends to trade have the same level of systematic risk as the market portfolio.
- The market portfolio's expected return is 10% pa.
Measure the net gain over the first year as an expected wealth increase at the end of the year.
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
Question 339 bond pricing, inflation, market efficiency, income and capital returns
Economic statistics released this morning were a surprise: they show a strong chance of consumer price inflation (CPI) reaching 5% pa over the next 2 years.
This is much higher than the previous forecast of 3% pa.
A vanilla fixed-coupon 2-year risk-free government bond was issued at par this morning, just before the economic news was released.
What is the expected change in bond price after the economic news this morning, and in the next 2 years? Assume that:
- Inflation remains at 5% over the next 2 years.
- Investors demand a constant real bond yield.
- The bond price falls by the (after-tax) value of the coupon the night before the ex-coupon date, as in real life.
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
Question 416 real estate, market efficiency, income and capital returns, DDM, CAPM
A residential real estate investor believes that house prices will grow at a rate of 5% pa and that rents will grow by 2% pa forever.
All rates are given as nominal effective annual returns. Assume that:
- His forecast is true.
- Real estate is and always will be fairly priced and the capital asset pricing model (CAPM) is true.
- Ignore all costs such as taxes, agent fees, maintenance and so on.
- All rental income cash flow is paid out to the owner, so there is no re-investment and therefore no additions or improvements made to the property.
- The non-monetary benefits of owning real estate and renting remain constant.
Which one of the following statements is NOT correct? Over time:
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Assume that there are no dividend payments so the entire 15% total return is all capital return.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% return lasts for the next 100 years (t=0 to 100), then reverts to 10% pa after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant. All returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
The efficient markets hypothesis (EMH) and no-arbitrage pricing theory are most closely related to which of the following concepts?
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Of the 15% pa total expected return, the dividend yield is expected to always be 7% pa and rest is the capital yield.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% total return lasts for the next 100 years (t=0 to 100), then reverts to 10% after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant, the dividends can only be re-invested at 10% pa and all returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
The average weekly earnings of an Australian adult worker before tax was $1,542.40 per week in November 2014 according to the Australian Bureau of Statistics. Therefore average annual earnings before tax were $80,204.80 assuming 52 weeks per year. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below:
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $80,204.80 per annum before-tax?
Question 448 franking credit, personal tax on dividends, imputation tax system
A small private company has a single shareholder. This year the firm earned a $100 profit before tax. All of the firm's after tax profits will be paid out as dividends to the owner.
The corporate tax rate is 30% and the sole shareholder's personal marginal tax rate is 45%.
The Australian imputation tax system applies because the company generates all of its income in Australia and pays corporate tax to the Australian Tax Office. Therefore all of the company's dividends are fully franked. The sole shareholder is an Australian for tax purposes and can therefore use the franking credits to offset his personal income tax liability.
What will be the personal tax payable by the shareholder and the corporate tax payable by the company?
A company announces that it will pay a dividend, as the market expected. The company's shares trade on the stock exchange which is open from 10am in the morning to 4pm in the afternoon each weekday. When would the share price be expected to fall by the amount of the dividend? Ignore taxes.
The share price is expected to fall during the:
A mining firm has just discovered a new mine. So far the news has been kept a secret.
The net present value of digging the mine and selling the minerals is $250 million, but $500 million of new equity and $300 million of new bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and equity and bond raising to shareholders simultaneously in the same announcement. The shares and bonds will be issued shortly after.
Once the announcement is made and the new shares and bonds are issued, what is the expected increase in the value of the firm's assets ##(\Delta V)##, market capitalisation of debt ##(\Delta D)## and market cap of equity ##(\Delta E)##? Assume that markets are semi-strong form efficient.
The triangle symbol ##\Delta## is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##\Delta V = \Delta D+ \Delta E##
Question 625 dividend re-investment plan, capital raising
Which of the following statements about dividend re-investment plans (DRP's) is NOT correct?
In late 2003 the listed bank ANZ announced a 2-for-11 rights issue to fund the takeover of New Zealand bank NBNZ. Below is the chronology of events:
- 23/10/2003. Share price closes at $18.30.
- 24/10/2003. 2-for-11 rights issue announced at a subscription price of $13. The proceeds of the rights issue will be used to acquire New Zealand bank NBNZ. Trading halt announced in morning before market opens.
- 28/10/2003. Trading halt lifted. Last (and only) day that shares trade cum-rights. Share price opens at $18.00 and closes at $18.14.
- 29/10/2003. Shares trade ex-rights.
All things remaining equal, what would you expect ANZ's stock price to open at on the first day that it trades ex-rights (29/10/2003)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
Question 708 continuously compounding rate, continuously compounding rate conversion
Convert a 10% continuously compounded annual rate ##(r_\text{cc annual})## into an effective annual rate ##(r_\text{eff annual})##. The equivalent effective annual rate is:
Question 767 idiom, corporate financial decision theory, no explanation
The sayings "Don't cry over spilt milk", "Don't regret the things that you can't change" and "What's done is done" are most closely related to which financial concept?
Question 768 accounting terminology, book and market values, no explanation
Accountants and finance professionals have lots of names for the same things which can be quite confusing.
Which of the following groups of items are NOT synonyms?
"Buy low, sell high" is a well-known saying. It suggests that investors should buy low then sell high, in that order.
How would you re-phrase that saying to describe short selling?
Question 770 expected and historical returns, income and capital returns, coupon rate, bond pricing
Which of the following statements is NOT correct? Assume that all events are a surprise and that all other things remain equal. So for example, don't assume that just because a company's dividends and profit rise that its required return will also rise, assume the required return stays the same.
Question 771 debt terminology, interest expense, interest tax shield, credit risk, no explanation
You deposit money into a bank account. Which of the following statements about this deposit is NOT correct?
Question 772 interest tax shield, capital structure, leverage
A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
One year ago you bought a $1,000,000 house partly funded using a mortgage loan. The loan size was $800,000 and the other $200,000 was your wealth or 'equity' in the house asset.
The interest rate on the home loan was 4% pa.
Over the year, the house produced a net rental yield of 2% pa and a capital gain of 2.5% pa.
Assuming that all cash flows (interest payments and net rental payments) were paid and received at the end of the year, and all rates are given as effective annual rates, what was the total return on your wealth over the past year?
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Below is a graph of 3 peoples’ utility functions, Mr Blue (U=W^(1/2) ), Miss Red (U=W/10) and Mrs Green (U=W^2/1000). Assume that each of them currently have $50 of wealth.
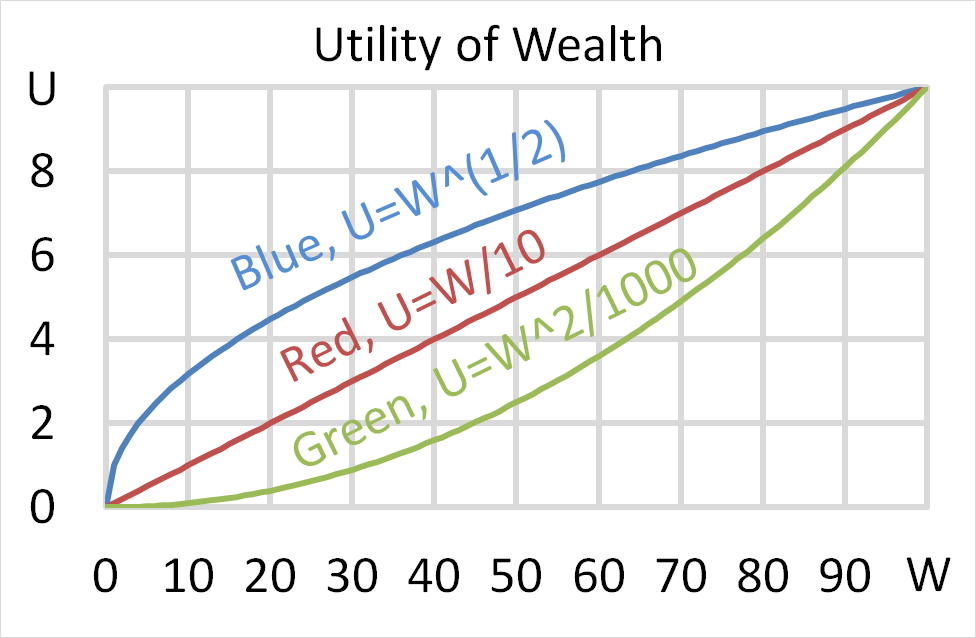
Which of the following statements about them is NOT correct?
(a) Mr Blue would prefer to invest his wealth in a well diversified portfolio of stocks rather than a single stock, assuming that all stocks had the same total risk and return.
The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
A stock has a beta of 0.5.
In the last 5 minutes, the federal government unexpectedly raised taxes. Over this time the share market fell by 3%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
The 'time value of money' is most closely related to which of the following concepts?
Question 657 systematic and idiosyncratic risk, CAPM, no explanation
A stock's required total return will decrease when its:
Question 658 CFFA, income statement, balance sheet, no explanation
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the income statement needed? Note that the income statement is sometimes also called the profit and loss, P&L, or statement of financial performance.
Question 659 APR, effective rate, effective rate conversion, no explanation
A home loan company advertises an interest rate of 9% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given with an accuracy of 4 decimal places.
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###A stock's total standard deviation of returns is 20% pa. The market portfolio's total standard deviation of returns is 15% pa. The beta of the stock is 0.8.
What is the stock's diversifiable standard deviation?
Question 662 APR, effective rate, effective rate conversion, no explanation
Which of the following interest rate labels does NOT make sense?
A firm has a debt-to-assets ratio of 20%. What is its debt-to-equity ratio?
Question 664 real and nominal returns and cash flows, inflation, no explanation
What is the present value of real payments of $100 every year forever, with the first payment in one year? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 2 for 3 rights issue at a subscription price of $8 when the pre-announcement stock price was $9. Assume that all investors use their rights to buy those extra shares.
What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
Which of the following is NOT a valid method for estimating the beta of a company's stock? Assume that markets are efficient, a long history of past data is available, the stock possesses idiosyncratic and market risk. The variances and standard deviations below denote total risks.
A stock's required total return will increase when its:
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the balance sheet needed? Note that the balance sheet is sometimes also called the statement of financial position.
An economy has only two investable assets: stocks and cash.
Stocks had a historical nominal average total return of negative two percent per annum (-2% pa) over the last 20 years. Stocks are liquid and actively traded. Stock returns are variable, they have risk.
Cash is riskless and has a nominal constant return of zero percent per annum (0% pa), which it had in the past and will have in the future. Cash can be kept safely at zero cost. Cash can be converted into shares and vice versa at zero cost.
The nominal total return of the shares over the next year is expected to be: