A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
Stocks in the United States usually pay quarterly dividends. For example, the retailer Wal-Mart Stores paid a $0.47 dividend every quarter over the 2013 calendar year and plans to pay a $0.48 dividend every quarter over the 2014 calendar year.
Using the dividend discount model and net present value techniques, calculate the stock price of Wal-Mart Stores assuming that:
- The time now is the beginning of January 2014. The next dividend of $0.48 will be received in 3 months (end of March 2014), with another 3 quarterly payments of $0.48 after this (end of June, September and December 2014).
- The quarterly dividend will increase by 2% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in 2015 will be $0.4896 (##=0.48×(1+0.02)^1##), with the first at the end of March 2015 and the last at the end of December 2015. In 2016 each quarterly dividend will be $0.499392 (##=0.48×(1+0.02)^2##), with the first at the end of March 2016 and the last at the end of December 2016, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- All cash flows and rates are nominal. Inflation is 3% pa.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
The saying "buy low, sell high" suggests that investors should make a:
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Alice buys a future from Chris.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Question 749 Multiples valuation, PE ratio, price to revenue ratio, price to book ratio, NPV
A real estate agent says that the price of a house in Sydney Australia is approximately equal to the gross weekly rent times 1000.
What type of valuation method is the real estate agent using?
A firm wishes to raise $30 million now. The firm's current market value of equity is $60m and the market price per share is $20. They estimate that they'll be able to issue shares in a rights issue at a subscription price of $15. Ignore the time value of money and assume that all shareholders exercise their rights. Which of the following statements is NOT correct?
Question 793 option, hedging, delta hedging, gamma hedging, gamma, Black-Scholes-Merton option pricing
A bank buys 1000 European put options on a $10 non-dividend paying stock at a strike of $12. The bank wishes to hedge this exposure. The bank can trade the underlying stocks and European call options with a strike price of 7 on the same stock with the same maturity. Details of the call and put options are given in the table below. Each call and put option is on a single stock.
| European Options on a Non-dividend Paying Stock | |||
| Description | Symbol | Put Values | Call Values |
| Spot price ($) | ##S_0## | 10 | 10 |
| Strike price ($) | ##K_T## | 12 | 7 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.4 | 0.4 |
| Option maturity (years) | ##T## | 1 | 1 |
| Option price ($) | ##p_0## or ##c_0## | 2.495350486 | 3.601466138 |
| ##N[d_1]## | ##\partial c/\partial S## | 0.888138405 | |
| ##N[d_2]## | ##N[d_2]## | 0.792946442 | |
| ##-N[-d_1]## | ##\partial p/\partial S## | -0.552034778 | |
| ##N[-d_2]## | ##N[-d_2]## | 0.207053558 | |
| Gamma | ##\Gamma = \partial^2 c/\partial S^2## or ##\partial^2 p/\partial S^2## | 0.098885989 | 0.047577422 |
| Theta | ##\Theta = \partial c/\partial T## or ##\partial p/\partial T## | 0.348152078 | 0.672379961 |
Which of the following statements is NOT correct?
Question 862 yield curve, bond pricing, bill pricing, monetary policy, no explanation
Refer to the below graph when answering the questions.
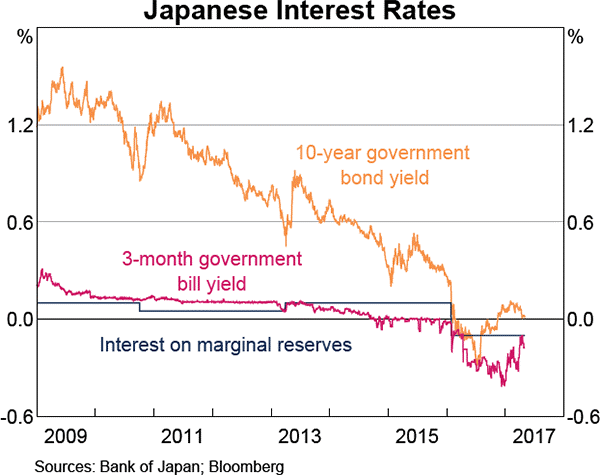
Which of the following statements is NOT correct?
Question 956 option, Black-Scholes-Merton option pricing, delta hedging, hedging
A bank sells a European call option on a non-dividend paying stock and delta hedges on a daily basis. Below is the result of their hedging, with columns representing consecutive days. Assume that there are 365 days per year and interest is paid daily in arrears.
| Delta Hedging a Short Call using Stocks and Debt | |||||||
| Description | Symbol | Days to maturity (T in days) | |||||
| 60 | 59 | 58 | 57 | 56 | 55 | ||
| Spot price ($) | S | 10000 | 10125 | 9800 | 9675 | 10000 | 10000 |
| Strike price ($) | K | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 |
| Risk free cont. comp. rate (pa) | r | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | σ | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| Option maturity (years) | T | 0.164384 | 0.161644 | 0.158904 | 0.156164 | 0.153425 | 0.150685 |
| Delta | N[d1] = dc/dS | 0.552416 | 0.582351 | 0.501138 | 0.467885 | 0.550649 | 0.550197 |
| Probability that S > K at maturity in risk neutral world | N[d2] | 0.487871 | 0.51878 | 0.437781 | 0.405685 | 0.488282 | 0.488387 |
| Call option price ($) | c | 685.391158 | 750.26411 | 567.990995 | 501.487157 | 660.982878 | ? |
| Stock investment value ($) | N[d1]*S | 5524.164129 | 5896.301781 | 4911.152036 | 4526.788065 | 5506.488143 | ? |
| Borrowing which partly funds stock investment ($) | N[d2]*K/e^(r*T) | 4838.772971 | 5146.037671 | 4343.161041 | 4025.300909 | 4845.505265 | ? |
| Interest expense from borrowing paid in arrears ($) | r*N[d2]*K/e^(r*T) | 0.662891 | 0.704985 | 0.594994 | 0.551449 | ? | |
| Gain on stock ($) | N[d1]*(SNew - SOld) | 69.052052 | -189.264008 | -62.642245 | 152.062648 | ? | |
| Gain on short call option ($) | -1*(cNew - cOld) | -64.872952 | 182.273114 | 66.503839 | -159.495721 | ? | |
| Net gain ($) | Gains - InterestExpense | 3.516209 | -7.695878 | 3.266599 | -7.984522 | ? | |
| Gamma | Γ = d^2c/dS^2 | 0.000244 | 0.00024 | 0.000255 | 0.00026 | 0.000253 | 0.000255 |
| Theta | θ = dc/dT | 2196.873429 | 2227.881353 | 2182.174706 | 2151.539751 | 2266.589184 | 2285.1895 |
In the last column when there are 55 days left to maturity there are missing values. Which of the following statements about those missing values is NOT correct?