One and a half years ago Frank bought a house for $600,000. Now it's worth only $500,000, based on recent similar sales in the area.
The expected total return on Frank's residential property is 7% pa.
He rents his house out for $1,600 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $18,617.27.
The future value of 12 months of rental payments one year in the future is $19,920.48.
What is the expected annual rental yield of the property? Ignore the costs of renting such as maintenance, real estate agent fees and so on.
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 407 income and capital returns, inflation, real and nominal returns and cash flows
A stock has a real expected total return of 7% pa and a real expected capital return of 2% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What is the nominal expected total return, capital return and dividend yield? The answers below are given in the same order.
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 575 inflation, real and nominal returns and cash flows
You expect a nominal payment of $100 in 5 years. The real discount rate is 10% pa and the inflation rate is 3% pa. Which of the following statements is NOT correct?
Which of the following statements about book and market equity is NOT correct?
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
Question 577 inflation, real and nominal returns and cash flows
What is the present value of a real payment of $500 in 2 years? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Question 554 inflation, real and nominal returns and cash flows
On his 20th birthday, a man makes a resolution. He will put $30 cash under his bed at the end of every month starting from today. His birthday today is the first day of the month. So the first addition to his cash stash will be in one month. He will write in his will that when he dies the cash under the bed should be given to charity.
If the man lives for another 60 years, how much money will be under his bed if he dies just after making his last (720th) addition?
Also, what will be the real value of that cash in today's prices if inflation is expected to 2.5% pa? Assume that the inflation rate is an effective annual rate and is not expected to change.
The answers are given in the same order, the amount of money under his bed in 60 years, and the real value of that money in today's prices.
You're considering making an investment in a particular company. They have preference shares, ordinary shares, senior debt and junior debt.
Which is the safest investment? Which has the highest expected returns?
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
What is the payback period of the project in years?
Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $500 at time 2 is actually earned smoothly from t=1 to t=2.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.
What is the net present value (NPV) of borrowing from your friend?
Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
Question 535 DDM, real and nominal returns and cash flows, stock pricing
You are an equities analyst trying to value the equity of the Australian telecoms company Telstra, with ticker TLS. In Australia, listed companies like Telstra tend to pay dividends every 6 months. The payment around August is called the final dividend and the payment around February is called the interim dividend. Both occur annually.
- Today is mid-March 2015.
- TLS's last interim dividend of $0.15 was one month ago in mid-February 2015.
- TLS's last final dividend of $0.15 was seven months ago in mid-August 2014.
Judging by TLS's dividend history and prospects, you estimate that the nominal dividend growth rate will be 1% pa. Assume that TLS's total nominal cost of equity is 6% pa. The dividends are nominal cash flows and the inflation rate is 2.5% pa. All rates are quoted as nominal effective annual rates. Assume that each month is exactly one twelfth (1/12) of a year, so you can ignore the number of days in each month.
Calculate the current TLS share price.
Question 488 income and capital returns, payout policy, payout ratio, DDM
Two companies BigDiv and ZeroDiv are exactly the same except for their dividend payouts.
BigDiv pays large dividends and ZeroDiv doesn't pay any dividends.
Currently the two firms have the same earnings, assets, number of shares, share price, expected total return and risk.
Assume a perfect world with no taxes, no transaction costs, no asymmetric information and that all assets including business projects are fairly priced and therefore zero-NPV.
All things remaining equal, which of the following statements is NOT correct?
A stock is expected to pay a dividend of $15 in one year (t=1), then $25 for 9 years after that (payments at t=2 ,3,...10), and on the 11th year (t=11) the dividend will be 2% less than at t=10, and will continue to shrink at the same rate every year after that forever. The required return of the stock is 10%. All rates are effective annual rates.
What is the price of the stock now?
Carlos and Edwin are brothers and they both love Holden Commodore cars.
Carlos likes to buy the latest Holden Commodore car for $40,000 every 4 years as soon as the new model is released. As soon as he buys the new car, he sells the old one on the second hand car market for $20,000. Carlos never has to bother with paying for repairs since his cars are brand new.
Edwin also likes Commodores, but prefers to buy 4-year old cars for $20,000 and keep them for 11 years until the end of their life (new ones last for 15 years in total but the 4-year old ones only last for another 11 years). Then he sells the old car for $2,000 and buys another 4-year old second hand car, and so on.
Every time Edwin buys a second hand 4 year old car he immediately has to spend $1,000 on repairs, and then $1,000 every year after that for the next 10 years. So there are 11 payments in total from when the second hand car is bought at t=0 to the last payment at t=10. One year later (t=11) the old car is at the end of its total 15 year life and can be scrapped for $2,000.
Assuming that Carlos and Edwin maintain their love of Commodores and keep up their habits of buying new ones and second hand ones respectively, how much larger is Carlos' equivalent annual cost of car ownership compared with Edwin's?
The real discount rate is 10% pa. All cash flows are real and are expected to remain constant. Inflation is forecast to be 3% pa. All rates are effective annual. Ignore capital gains tax and tax savings from depreciation since cars are tax-exempt for individuals.
You own a nice suit which you wear once per week on nights out. You bought it one year ago for $600. In your experience, suits used once per week last for 6 years. So you expect yours to last for another 5 years.
Your younger brother said that retro is back in style so he wants to wants to borrow your suit once a week when he goes out. With the increased use, your suit will only last for another 4 years rather than 5.
What is the present value of the cost of letting your brother use your current suit for the next 4 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new suit when your current one wears out and your brother will not use the new one; your brother will only use your current suit so he will only use it for the next four years; and the price of a new suit never changes.
An industrial chicken farmer grows chickens for their meat. Chickens:
- Cost $0.50 each to buy as chicks. They are bought on the day they’re born, at t=0.
- Grow at a rate of $0.70 worth of meat per chicken per week for the first 6 weeks (t=0 to t=6).
- Grow at a rate of $0.40 worth of meat per chicken per week for the next 4 weeks (t=6 to t=10) since they’re older and grow more slowly.
- Feed costs are $0.30 per chicken per week for their whole life. Chicken feed is bought and fed to the chickens once per week at the beginning of the week. So the first amount of feed bought for a chicken at t=0 costs $0.30, and so on.
- Can be slaughtered (killed for their meat) and sold at no cost at the end of the week. The price received for the chicken is their total value of meat (note that the chicken grows fast then slow, see above).
The required return of the chicken farm is 0.5% given as an effective weekly rate.
Ignore taxes and the fixed costs of the factory. Ignore the chicken’s welfare and other environmental and ethical concerns.
Find the equivalent weekly cash flow of slaughtering a chicken at 6 weeks and at 10 weeks so the farmer can figure out the best time to slaughter his chickens. The choices below are given in the same order, 6 and 10 weeks.
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
What is the net present value (NPV) of undertaking a full-time Australian undergraduate business degree as an Australian citizen? Only include the cash flows over the duration of the degree, ignore any benefits or costs of the degree after it's completed.
Assume the following:
- The degree takes 3 years to complete and all students pass all subjects.
- There are 2 semesters per year and 4 subjects per semester.
- University fees per subject per semester are $1,277, paid at the start of each semester. Fees are expected to remain constant in real terms for the next 3 years.
- There are 52 weeks per year.
- The first semester is just about to start (t=0). The first semester lasts for 19 weeks (t=0 to 19).
- The second semester starts immediately afterwards (t=19) and lasts for another 19 weeks (t=19 to 38).
- The summer holidays begin after the second semester ends and last for 14 weeks (t=38 to 52). Then the first semester begins the next year, and so on.
- Working full time at the grocery store instead of studying full-time pays $20/hr and you can work 35 hours per week. Wages are paid at the end of each week and are expected to remain constant in real terms.
- Full-time students can work full-time during the summer holiday at the grocery store for the same rate of $20/hr for 35 hours per week.
- The discount rate is 9.8% pa. All rates and cash flows are real. Inflation is expected to be 3% pa. All rates are effective annual.
The NPV of costs from undertaking the university degree is:
You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.
How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.
Your main expense is fuel for your car which costs $100 per month. You just refueled, so you won't need any more fuel for another month (first payment at t=1 month).
You have $2,500 in a bank account which pays interest at a rate of 6% pa, payable monthly. Interest rates are not expected to change.
Assuming that you have no income, in how many months time will you not have enough money to fully refuel your car?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
To your surprise, you can actually afford to pay $2,000 per month and your mortgage allows early repayments without fees. If you maintain these higher monthly payments, how long will it take to pay off your mortgage?
You're trying to save enough money for a deposit to buy a house. You want to buy a house worth $400,000 and the bank requires a 20% deposit ($80,000) before it will give you a loan for the other $320,000 that you need.
You currently have no savings, but you just started working and can save $2,000 per month, with the first payment in one month from now. Bank interest rates on savings accounts are 4.8% pa with interest paid monthly and interest rates are not expected to change.
How long will it take to save the $80,000 deposit? Round your answer up to the nearest month.
A student won $1m in a lottery. Currently the money is in a bank account which pays interest at 6% pa, given as an APR compounding per month.
She plans to spend $20,000 at the beginning of every month from now on (so the first withdrawal will be at t=0). After each withdrawal, she will check how much money is left in the account. When there is less than $500,000 left, she will donate that remaining amount to charity.
In how many months will she make her last withdrawal and donate the remainder to charity?
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
The following cash flows are expected:
- 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
- 1 payment of $400 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which firms tend to have high forward-looking price-earnings (PE) ratios?
Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
Question 64 inflation, real and nominal returns and cash flows, APR, effective rate
In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.
The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Question 249 equivalent annual cash flow, effective rate conversion
Details of two different types of desserts or edible treats are given below:
- High-sugar treats like candy, chocolate and ice cream make a person very happy. High sugar treats are cheap at only $2 per day.
- Low-sugar treats like nuts, cheese and fruit make a person equally happy if these foods are of high quality. Low sugar treats are more expensive at $4 per day.
The advantage of low-sugar treats is that a person only needs to pay the dentist $2,000 for fillings and root canal therapy once every 15 years. Whereas with high-sugar treats, that treatment needs to be done every 5 years.
The real discount rate is 10%, given as an effective annual rate. Assume that there are 365 days in every year and that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the equivalent annual cash flow (EAC) of the high-sugar treats and low-sugar treats, including dental costs. The below choices are listed in that order.
Ignore the pain of dental therapy, personal preferences and other factors.
Question 210 real estate, inflation, real and nominal returns and cash flows, income and capital returns
Assume that the Gordon Growth Model (same as the dividend discount model or perpetuity with growth formula) is an appropriate method to value real estate.
An old rule of thumb in the real estate industry is that properties should yield a 5% pa rental return. Some investors also regard property to be as risky as the stock market, therefore property is thought to have a required total return of 9% pa which is the average total return on the stock market including dividends.
Assume that all returns are effective annual rates and they are nominal (not reduced by inflation). Inflation is expected to be 2% pa.
You're considering purchasing an investment property which has a rental yield of 5% pa and you expect it to have the same risk as the stock market. Select the most correct statement about this property.
Question 529 DDM, real and nominal returns and cash flows, inflation, real estate, no explanation
If housing rents are constrained from growing more than the maximum target inflation rate, and houses can be priced as a perpetuity of growing net rental cash flows, then what is the implication for house prices, all things remaining equal? Select the most correct answer.
Background: Since 1990, many central banks across the world have become 'inflation targeters'. They have adopted a policy of trying to keep inflation in a predictable narrow range, with the hope of encouraging long-term lending to fund more investment and maintain higher GDP growth.
Australia's central bank, the Reserve Bank of Australia (RBA), has specifically stated their inflation target range is between 2 and 3% pa.
Some Australian residential property market commentators suggest that because rental costs comprise a large part of the Australian consumer price index (CPI), rent costs across the nation cannot significantly exceed the maximum inflation target range of 3% pa without the prices of other goods growing by less than the target range for long periods, which is unlikely.
For a price of $129, Joanne will sell you a share which is expected to pay a $30 dividend in one year, and a $10 dividend every year after that forever. So the stock's dividends will be $30 at t=1, $10 at t=2, $10 at t=3, and $10 forever onwards.
The required return of the stock is 10% pa.
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
Question 48 IRR, NPV, bond pricing, premium par and discount bonds, market efficiency
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
In Australia, domestic university students are allowed to buy concession tickets for the bus, train and ferry which sell at a discount of 50% to full-price tickets.
The Australian Government do not allow international university students to buy concession tickets, they have to pay the full price.
Some international students see this as unfair and they are willing to pay for fake university identification cards which have the concession sticker.
What is the most that an international student would be willing to pay for a fake identification card?
Assume that international students:
- consider buying their fake card on the morning of the first day of university from their neighbour, just before they leave to take the train into university.
- buy their weekly train tickets on the morning of the first day of each week.
- ride the train to university and back home again every day seven days per week until summer holidays 40 weeks from now. The concession card only lasts for those 40 weeks. Assume that there are 52 weeks in the year for the purpose of interest rate conversion.
- a single full-priced one-way train ride costs $5.
- have a discount rate of 11% pa, given as an effective annual rate.
Approach this question from a purely financial view point, ignoring the illegality, embarrassment and the morality of committing fraud.
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A student just won the lottery. She won $1 million in cash after tax. She is trying to calculate how much she can spend per month for the rest of her life. She assumes that she will live for another 60 years. She wants to withdraw equal amounts at the beginning of every month, starting right now.
All of the cash is currently sitting in a bank account which pays interest at a rate of 6% pa, given as an APR compounding per month. On her last withdrawal, she intends to have nothing left in her bank account. How much can she withdraw at the beginning of each month?
A mature firm has constant expected future earnings and dividends. Both amounts are equal. So earnings and dividends are expected to be equal and unchanging.
Which of the following statements is NOT correct?
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 6.5 years from now (first payment at t=6.5).
- A single payment of $500 in 4 years and 3 months (t=4.25) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 547 PE ratio, Multiples valuation, DDM, income and capital returns, no explanation
A firm pays out all of its earnings as dividends. Because of this, the firm has no real growth in earnings, dividends or stock price since there is no re-investment back into the firm to buy new assets and make higher earnings. The dividend discount model is suitable to value this company.
The firm's revenues and costs are expected to increase by inflation in the foreseeable future. The firm has no debt. It operates in the services industry and has few physical assets so there is negligible depreciation expense and negligible net working capital required.
Which of the following statements about this firm's PE ratio is NOT correct? The PE ratio should:
Note: The inverse of x is 1/x.
Question 548 equivalent annual cash flow, time calculation, no explanation
An Apple iPhone 6 smart phone can be bought now for $999. An Android Kogan Agora 4G+ smart phone can be bought now for $240.
If the Kogan phone lasts for one year, approximately how long must the Apple phone last for to have the same equivalent annual cost?
Assume that both phones have equivalent features besides their lifetimes, that both are worthless once they've outlasted their life, the discount rate is 10% pa given as an effective annual rate, and there are no extra costs or benefits from either phone.
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.
Ignoring the costs of financial distress, which of the following statements is NOT correct:
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
Find the cash flow from assets (CFFA) of the following project.
| Project Data | ||
| Project life | 2 years | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year for tax purposes | $1m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $3 | |
| Fixed costs per year, paid at the end of each year | $1.5m | |
| Tax rate | 30% | |
Note 1: The equipment will have a book value of $4m at the end of the project for tax purposes. However, the equipment is expected to fetch $0.9 million when it is sold at t=2.
Note 2: Due to the project, the firm will have to purchase $0.8m of inventory initially, which it will sell at t=1. The firm will buy another $0.8m at t=1 and sell it all again at t=2 with zero inventory left. The project will have no effect on the firm's current liabilities.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
Value the following business project to manufacture a new product.
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $3m | |
| Expected sale price of equipment at end of project | $0.6m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense per year | 0 | |
| Tax rate | 30% | |
| Weighted average cost of capital after tax per annum | 10% | |
Notes
- The firm's current assets and current liabilities are $3m and $2m respectively right now. This net working capital will not be used in this project, it will be used in other unrelated projects.
Due to the project, current assets (mostly inventory) will grow by $2m initially (at t = 0), and then by $0.2m at the end of the first year (t=1).
Current liabilities (mostly trade creditors) will increase by $0.1m at the end of the first year (t=1).
At the end of the project, the net working capital accumulated due to the project can be sold for the same price that it was bought. - The project cost $0.5m to research which was incurred one year ago.
Assumptions
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 3% pa.
- All rates are given as effective annual rates.
- The business considering the project is run as a 'sole tradership' (run by an individual without a company) and is therefore eligible for a 50% capital gains tax discount when the equipment is sold, as permitted by the Australian Tax Office.
What is the expected net present value (NPV) of the project?
Over the next year, the management of an unlevered company plans to:
- Achieve firm free cash flow (FFCF or CFFA) of $1m.
- Pay dividends of $1.8m
- Complete a $1.3m share buy-back.
- Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Scubar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 60 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 90 | |
| Taxes at 30% | 27 | |
| Net income | 63 | |
| Scubar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 60 | 50 |
| Trade debtors | 19 | 6 |
| Rent paid in advance | 3 | 2 |
| PPE | 420 | 400 |
| Total assets | 502 | 458 |
| Trade creditors | 10 | 8 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 130 | 130 |
| Retained profits | 162 | 130 |
| Total L and OE | 502 | 458 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
Let the 'income return' of a bond be the coupon at the end of the period divided by the market price now at the start of the period ##(C_1/P_0)##. The expected income return of a premium fixed coupon bond is:
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
Question 56 income and capital returns, bond pricing, premium par and discount bonds
Which of the following statements about risk free government bonds is NOT correct?
Hint: Total return can be broken into income and capital returns as follows:
###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###
The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.
Here's the Dividend Discount Model, used to price stocks:
### p_0=\frac{d_1}{r-g} ###
All rates are effective annual rates and the cash flows (##d_1##) are received every year. Note that the r and g terms in the above DDM could also be labelled: ###r = r_{\text{total, 0}\rightarrow\text{1yr, eff 1yr}}### ###g = r_{\text{capital, 0}\rightarrow\text{1yr, eff 1yr}}### Which of the following statements is NOT correct?
Question 213 income and capital returns, bond pricing, premium par and discount bonds
The coupon rate of a fixed annual-coupon bond is constant (always the same).
What can you say about the income return (##r_\text{income}##) of a fixed annual coupon bond? Remember that:
###r_\text{total} = r_\text{income} + r_\text{capital}###
###r_\text{total, 0 to 1} = \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0}###
Assume that there is no change in the bond's total annual yield to maturity from when it is issued to when it matures.
Select the most correct statement.
From its date of issue until maturity, the income return of a fixed annual coupon:
The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):
###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###
Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:
###r_\text{total}=r_\text{income}+r_\text{capital}###
So the total return of an asset is the income component plus the capital or price growth component.
Another way to break up total return is to use the Capital Asset Pricing Model:
###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###
###r_\text{total}=r_\text{time value}+r_\text{risk premium}###
So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.
Using the above theory and your general knowledge, which of the below equations, if any, are correct?
(I) ##r_\text{income}=r_\text{time value}##
(II) ##r_\text{income}=r_\text{risk premium}##
(III) ##r_\text{capital}=r_\text{time value}##
(IV) ##r_\text{capital}=r_\text{risk premium}##
(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##
Which of the equations are correct?
A company's shares just paid their annual dividend of $2 each.
The stock price is now $40 (just after the dividend payment). The annual dividend is expected to grow by 3% every year forever. The assumptions of the dividend discount model are valid for this company.
What do you expect the effective annual dividend yield to be in 3 years (dividend yield from t=3 to t=4)?
Question 415 income and capital returns, real estate, no explanation
You just bought a residential apartment as an investment property for $500,000.
You intend to rent it out to tenants. They are ready to move in, they would just like to know how much the monthly rental payments will be, then they will sign a twelve-month lease.
You require a total return of 8% pa and a rental yield of 5% pa.
What would the monthly paid-in-advance rental payments have to be this year to receive that 5% annual rental yield?
Also, if monthly rental payments can be increased each year when a new lease agreement is signed, by how much must you increase rents per year to realise the 8% pa total return on the property?
Ignore all taxes and the costs of renting such as maintenance costs, real estate agent fees, utilities and so on. Assume that there will be no periods of vacancy and that tenants will promptly pay the rental prices you charge.
Note that the first rental payment will be received at t=0. The first lease agreement specifies the first 12 equal payments from t=0 to 11. The next lease agreement can have a rental increase, so the next twelve equal payments from t=12 to 23 can be higher than previously, and so on forever.
Question 455 income and capital returns, payout policy, DDM, market efficiency
A fairly priced unlevered firm plans to pay a dividend of $1 next year (t=1) which is expected to grow by 3% pa every year after that. The firm's required return on equity is 8% pa.
The firm is thinking about reducing its future dividend payments by 10% so that it can use the extra cash to invest in more projects which are expected to return 8% pa, and have the same risk as the existing projects. Therefore, next year's dividend will be $0.90. No new equity or debt will be issued to fund the new projects, they'll all be funded by the cut in dividends.
What will be the stock's new annual capital return (proportional increase in price per year) if the change in payout policy goes ahead?
Assume that payout policy is irrelevant to firm value (so there's no signalling effects) and that all rates are effective annual rates.
Question 539 debt terminology, fully amortising loan, bond pricing
A 'fully amortising' loan can also be called a:
Question 545 income and capital returns, fully amortising loan, no explanation
Which of the following statements about the capital and income returns of a 25 year fully amortising loan asset is correct?
Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.
Over the 25 years from issuance to maturity, a fully amortising loan's expected annual effective:
For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.
The required return of the stock is 10% pa.
A highly levered risky firm is trying to raise more debt. The types of debt being considered, in no particular order, are senior bonds, junior bonds, bank accepted bills, promissory notes and bank loans.
Which of these forms of debt is the safest from the perspective of the debt investors who are thinking of investing in the firm's new debt?
An established mining firm announces that it expects large losses over the following year due to flooding which has temporarily stalled production at its mines. Which statement(s) are correct?
(i) If the firm adheres to a full dividend payout policy it will not pay any dividends over the following year.
(ii) If the firm wants to signal that the loss is temporary it will maintain the same level of dividends. It can do this so long as it has enough retained profits.
(iii) By law, the firm will be unable to pay a dividend over the following year because it cannot pay a dividend when it makes a loss.
Select the most correct response:
Question 104 CAPM, payout policy, capital structure, Miller and Modigliani, risk
Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.
For a firm operating in this perfect world, which statement(s) are correct?
(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.
(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.
(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.
Select the most correct response:
Harvey Norman the large retailer often runs sales advertising 2 years interest free when you purchase its products. This offer can be seen as a free personal loan from Harvey Norman to its customers.
Assume that banks charge an interest rate on personal loans of 12% pa given as an APR compounding per month. This is the interest rate that Harvey Norman deserves on the 2 year loan it extends to its customers. Therefore Harvey Norman must implicitly include the cost of this loan in the advertised sale price of its goods.
If you were a customer buying from Harvey Norman, and you were paying immediately, not in 2 years, what is the minimum percentage discount to the advertised sale price that you would insist on? (Hint: if it makes it easier, assume that you’re buying a product with an advertised price of $100).
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0 | 6 | 12 | 18 | 20 | ... |
After year 4, the dividend will grow in perpetuity at 5% pa. The required return of the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in 7 years (t = 7), just after the dividend at that time has been paid?
A very low-risk stock just paid its semi-annual dividend of $0.14, as it has for the last 5 years. You conservatively estimate that from now on the dividend will fall at a rate of 1% every 6 months.
If the stock currently sells for $3 per share, what must be its required total return as an effective annual rate?
If risk free government bonds are trading at a yield of 4% pa, given as an effective annual rate, would you consider buying or selling the stock?
The stock's required total return is:
Question 241 Miller and Modigliani, leverage, payout policy, diversification, NPV
One of Miller and Modigliani's (M&M's) important insights is that a firm's managers should not try to achieve a particular level of leverage in a world with zero taxes and perfect information since investors can make their own leverage. Therefore corporate capital structure policy is irrelevant since investors can achieve their own desired leverage at the personal level by borrowing or lending on their own.
This principal of 'home-made' or 'do-it-yourself' leverage can also be applied to other topics. Read the following statements to decide which are true:
(I) Payout policy: a firm's managers should not try to achieve a particular pattern of equity payout.
(II) Agency costs: a firm's managers should not try to minimise agency costs.
(III) Diversification: a firm's managers should not try to diversify across industries.
(IV) Shareholder wealth: a firm's managers should not try to maximise shareholders' wealth.
Which of the above statement(s) are true?
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the end-of-year amount, paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
How much money do you expect to have in the fund in 40 years? Also, what is the future value of the fees that the fund expects to earn from you? Give both amounts as future values in 40 years. Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
- The fund invests its fees in the same companies as it invests your funds in, but with no fees.
The below answer choices list your expected wealth in 40 years and then the fund's expected wealth in 40 years.
A share currently worth $100 is expected to pay a constant dividend of $4 for the next 5 years with the first dividend in one year (t=1) and the last in 5 years (t=5).
The total required return is 10% pa.
What do you expected the share price to be in 5 years, just after the dividend at that time has been paid?
Question 659 APR, effective rate, effective rate conversion, no explanation
A home loan company advertises an interest rate of 9% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given with an accuracy of 4 decimal places.
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Currently, a mining company has a share price of $6 and pays constant annual dividends of $0.50. The next dividend will be paid in 1 year. Suddenly and unexpectedly the mining company announces that due to higher than expected profits, all of these windfall profits will be paid as a special dividend of $0.30 in 1 year.
If investors believe that the windfall profits and dividend is a one-off event, what will be the new share price? If investors believe that the additional dividend is actually permanent and will continue to be paid, what will be the new share price? Assume that the required return on equity is unchanged. Choose from the following, where the first share price includes the one-off increase in earnings and dividends for the first year only ##(P_\text{0 one-off})## , and the second assumes that the increase is permanent ##(P_\text{0 permanent})##:
Note: When a firm makes excess profits they sometimes pay them out as special dividends. Special dividends are just like ordinary dividends but they are one-off and investors do not expect them to continue, unlike ordinary dividends which are expected to persist.
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
The 'time value of money' is most closely related to which of the following concepts?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the price of the stock now?
A three year corporate bond yields 12% pa with a coupon rate of 10% pa, paid semi-annually.
Find the effective six month yield, effective annual yield and the effective daily yield. Assume that each month has 30 days and that there are 360 days in a year.
All answers are given in the same order:
##r_\text{eff semi-annual}##, ##r_\text{eff yearly}##, ##r_\text{eff daily}##.
Question 108 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 1 year zero coupon bond at a yield of 10% pa, and
- A 2 year zero coupon bond at a yield of 8% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 6% pa.
- Stock A has an expected return of 5% pa.
- Stock B has an expected return of 10% pa.
What portfolio weights should the investor have in stocks A and B respectively?
Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.
What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
What is the correlation of a variable X with a constant C?
The corr(X, C) or ##\rho_{X,C}## equals:
Question 558 portfolio weights, portfolio return, short selling
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 16% pa.
- Stock A has an expected return of 8% pa.
- Stock B has an expected return of 12% pa.
What portfolio weights should the investor have in stocks A and B respectively?
What is the covariance of a variable X with itself?
The cov(X, X) or ##\sigma_{X,X}## equals:
A company announces that it will pay a dividend, as the market expected. The company's shares trade on the stock exchange which is open from 10am in the morning to 4pm in the afternoon each weekday. When would the share price be expected to fall by the amount of the dividend? Ignore taxes.
The share price is expected to fall during the:
Question 566 capital structure, capital raising, rights issue, on market repurchase, dividend, stock split, bonus issue
A company's share price fell by 20% and its number of shares rose by 25%. Assume that there are no taxes, no signalling effects and no transaction costs.
Which one of the following corporate events may have happened?
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
There are a number of ways that assets can be depreciated. Generally the government's tax office stipulates a certain method.
But if it didn't, what would be the ideal way to depreciate an asset from the perspective of a businesses owner?
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
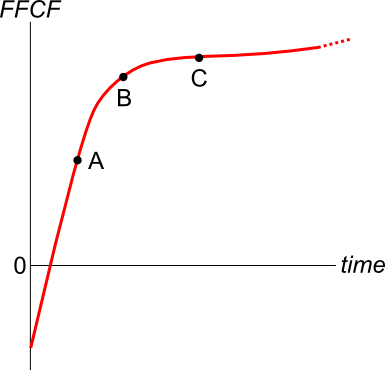
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
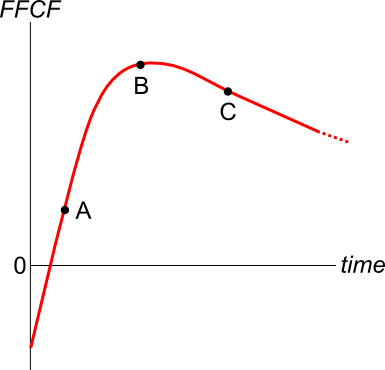
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
Question 419 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM, no explanation
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $6m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 9m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $6 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense in first year (at t=1) | $0.53m | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.08 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-assets ratio | 50% | |
Notes
- Due to the project, current assets will increase by $5m now (t=0) and fall by $5m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-assets ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Find the cash flow from assets (CFFA) of the following project.
| Project Data | |
| Project life | 2 years |
| Initial investment in equipment | $8m |
| Depreciation of equipment per year for tax purposes | $3m |
| Unit sales per year | 10m |
| Sale price per unit | $9 |
| Variable cost per unit | $4 |
| Fixed costs per year, paid at the end of each year | $2m |
| Tax rate | 30% |
Note 1: Due to the project, the firm will have to purchase $40m of inventory initially (at t=0). Half of this inventory will be sold at t=1 and the other half at t=2.
Note 2: The equipment will have a book value of $2m at the end of the project for tax purposes. However, the equipment is expected to fetch $1m when it is sold. Assume that the full capital loss is tax-deductible and taxed at the full corporate tax rate.
Note 3: The project will be fully funded by equity which investors will expect to pay dividends totaling $10m at the end of each year.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
A company has:
- 50 million shares outstanding.
- The market price of one share is currently $6.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts believe that the company's ordinary shares have a beta of 2.
- The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
- The company's debentures are publicly traded and their market price is equal to 90% of their face value.
- The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A company has:
- 10 million common shares outstanding, each trading at a price of $90.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant dividend of 9% of par. They currently trade at a price of $120 each.
- Debentures that have a total face value of $60,000,000 and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 90% of their face value.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts estimate that the company's common stock has a beta of 1.2. The corporate tax rate is 30%.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
Question 237 WACC, Miller and Modigliani, interest tax shield
Which of the following discount rates should be the highest for a levered company? Ignore the costs of financial distress.
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
Question 99 capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.
Assume that:
- The firm and individual investors can borrow at the same rate and have the same tax rates.
- The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
- There are no market frictions relating to debt such as asymmetric information or transaction costs.
- Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.
According to Miller and Modigliani's theory, which statement is correct?
Question 397 financial distress, leverage, capital structure, NPV
A levered firm has a market value of assets of $10m. Its debt is all comprised of zero-coupon bonds which mature in one year and have a combined face value of $9.9m.
Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.
Therefore the current market capitalisation of debt ##(D_0)## is $9m and equity ##(E_0)## is $1m.
A new project presents itself which requires an investment of $2m and will provide a:
- $6.6m cash flow with probability 0.5 in the good state of the world, and a
- -$4.4m (notice the negative sign) cash flow with probability 0.5 in the bad state of the world.
The project can be funded using the company's excess cash, no debt or equity raisings are required.
What would be the new market capitalisation of equity ##(E_\text{0, with project})## if shareholders vote to proceed with the project, and therefore should shareholders proceed with the project?
Question 398 financial distress, capital raising, leverage, capital structure, NPV
A levered firm has zero-coupon bonds which mature in one year and have a combined face value of $9.9m.
Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.
In one year the firm's assets will be worth:
- $13.2m with probability 0.5 in the good state of the world, or
- $6.6m with probability 0.5 in the bad state of the world.
A new project presents itself which requires an investment of $2m and will provide a certain cash flow of $3.3m in one year.
The firm doesn't have any excess cash to make the initial $2m investment, but the funds can be raised from shareholders through a fairly priced rights issue. Ignore all transaction costs.
Should shareholders vote to proceed with the project and equity raising? What will be the gain in shareholder wealth if they decide to proceed?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
Three important classes of investable risky assets are:
- Corporate debt which has low total risk,
- Real estate which has medium total risk,
- Equity which has high total risk.
Assume that the correlation between total returns on:
- Corporate debt and real estate is 0.1,
- Corporate debt and equity is 0.1,
- Real estate and equity is 0.5.
You are considering investing all of your wealth in one or more of these asset classes. Which portfolio will give the lowest total risk? You are restricted from shorting any of these assets. Disregard returns and the risk-return trade-off, pretend that you are only concerned with minimising risk.
The accounting identity states that the book value of a company's assets (A) equals its liabilities (L) plus owners equity (OE), so A = L + OE.
The finance version states that the market value of a company's assets (V) equals the market value of its debt (D) plus equity (E), so V = D + E.
Therefore a business's assets can be seen as a portfolio of the debt and equity that fund the assets.
Let ##\sigma_\text{V total}^2## be the total variance of returns on assets, ##\sigma_\text{V syst}^2## be the systematic variance of returns on assets, and ##\sigma_\text{V idio}^2## be the idiosyncratic variance of returns on assets, and ##\rho_\text{D idio, E idio}## be the correlation between the idiosyncratic returns on debt and equity.
Which of the following equations is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
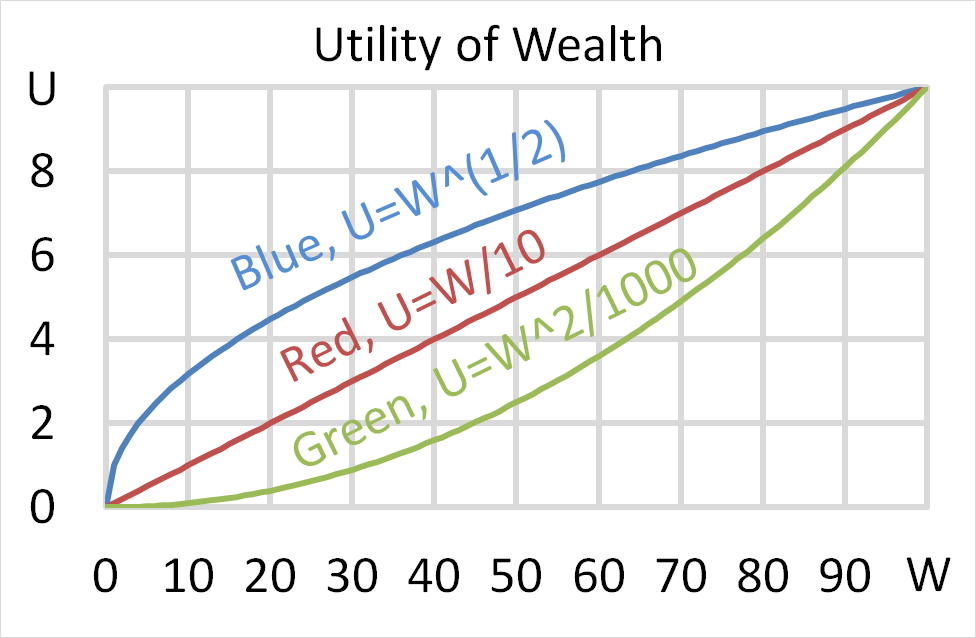
Question 700 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?
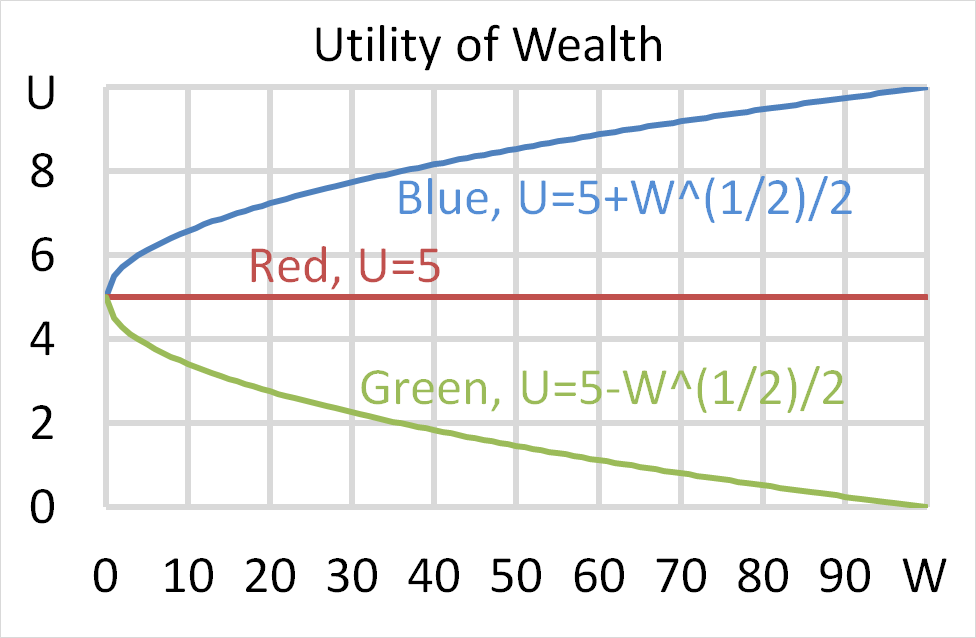
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
If a variable, say X, is normally distributed with mean ##\mu## and variance ##\sigma^2## then mathematicians write ##X \sim \mathcal{N}(\mu, \sigma^2)##.
If a variable, say Y, is log-normally distributed and the underlying normal distribution has mean ##\mu## and variance ##\sigma^2## then mathematicians write ## Y \sim \mathbf{ln} \mathcal{N}(\mu, \sigma^2)##.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Select the most correct statement:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.

Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 723 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 99 | -0.010050 | 0.990000 | -0.010000 |
| 2 | 180.40 | 0.600057 | 1.822222 | 0.822222 |
| 3 | 112.73 | 0.470181 | 0.624889 | 0.375111 |
| Arithmetic average | 0.0399 | 1.1457 | 0.1457 | |
| Arithmetic standard deviation | 0.4384 | 0.5011 | 0.5011 | |
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 2 for 3 rights issue at a subscription price of $8 when the pre-announcement stock price was $9. Assume that all investors use their rights to buy those extra shares.
What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.