The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
What is the Internal Rate of Return (IRR) of the project detailed in the table below?
Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
What is the payback period of the project in years?
Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $500 at time 2 is actually earned smoothly from t=1 to t=2.
The below graph shows a project's net present value (NPV) against its annual discount rate.
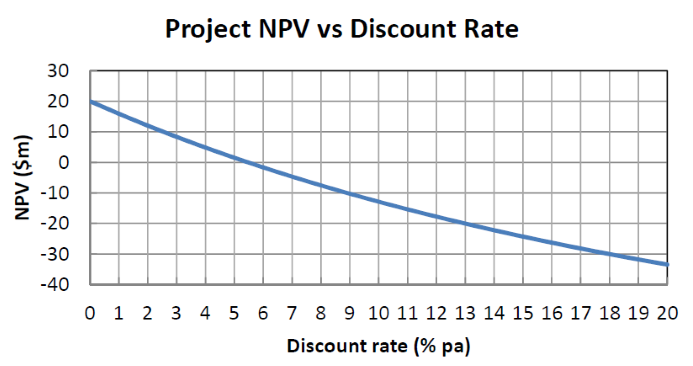
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
The below graph shows a project's net present value (NPV) against its annual discount rate.

Which of the following statements is NOT correct?
A firm is considering a business project which costs $11m now and is expected to pay a constant $1m at the end of every year forever.
Assume that the initial $11m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
Question 579 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to double if the price grows by 10% pa?
Question 580 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to quadruple (be four times as big, say from $1 to $4) if the price grows by 15% pa?
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
The saying "buy low, sell high" suggests that investors should make a:
Total cash flows can be broken into income and capital cash flows. What is the name given to the income cash flow from owning shares?
An asset's total expected return over the next year is given by:
###r_\text{total} = \dfrac{c_1+p_1-p_0}{p_0} ###
Where ##p_0## is the current price, ##c_1## is the expected income in one year and ##p_1## is the expected price in one year. The total return can be split into the income return and the capital return.
Which of the following is the expected capital return?
A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).
What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
A share was bought for $30 (at t=0) and paid its annual dividend of $6 one year later (at t=1).
Just after the dividend was paid, the share price fell to $27 (at t=1). What were the total, capital and income returns given as effective annual rates?
The choices are given in the same order:
##r_\text{total}## , ##r_\text{capital}## , ##r_\text{dividend}##.
Which of the following equations is NOT equal to the total return of an asset?
Let ##p_0## be the current price, ##p_1## the expected price in one year and ##c_1## the expected income in one year.
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 295 inflation, real and nominal returns and cash flows, NPV
When valuing assets using discounted cash flow (net present value) methods, it is important to consider inflation. To properly deal with inflation:
(I) Discount nominal cash flows by nominal discount rates.
(II) Discount nominal cash flows by real discount rates.
(III) Discount real cash flows by nominal discount rates.
(IV) Discount real cash flows by real discount rates.
Which of the above statements is or are correct?
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 363 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 8% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 407 income and capital returns, inflation, real and nominal returns and cash flows
A stock has a real expected total return of 7% pa and a real expected capital return of 2% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What is the nominal expected total return, capital return and dividend yield? The answers below are given in the same order.
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
In the 'Austin Powers' series of movies, the character Dr. Evil threatens to destroy the world unless the United Nations pays him a ransom (video 1, video 2). Dr. Evil makes the threat on two separate occasions:
- In 1969 he demands a ransom of $1 million (=10^6), and again;
- In 1997 he demands a ransom of $100 billion (=10^11).
If Dr. Evil's demands are equivalent in real terms, in other words $1 million will buy the same basket of goods in 1969 as $100 billion would in 1997, what was the implied inflation rate over the 28 years from 1969 to 1997?
The answer choices below are given as effective annual rates:
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.
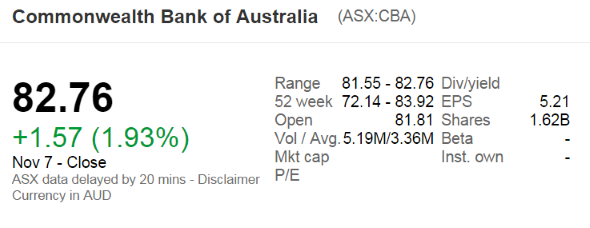
What was CBA's market capitalisation of equity?
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.
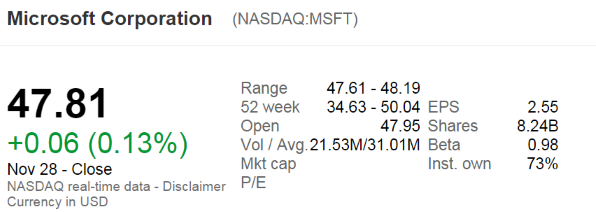
What was MSFT's market capitalisation of equity?
Which of the following statements about book and market equity is NOT correct?
Question 444 investment decision, corporate financial decision theory
The investment decision primarily affects which part of a business?
Question 446 working capital decision, corporate financial decision theory
The working capital decision primarily affects which part of a business?
Question 445 financing decision, corporate financial decision theory
The financing decision primarily affects which part of a business?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
Question 443 corporate financial decision theory, investment decision, financing decision, working capital decision, payout policy
Business people make lots of important decisions. Which of the following is the most important long term decision?
You're considering making an investment in a particular company. They have preference shares, ordinary shares, senior debt and junior debt.
Which is the safest investment? Which has the highest expected returns?
A newly floated farming company is financed with senior bonds, junior bonds, cumulative non-voting preferred stock and common stock. The new company has no retained profits and due to floods it was unable to record any revenues this year, leading to a loss. The firm is not bankrupt yet since it still has substantial contributed equity (same as paid-up capital).
On which securities must it pay interest or dividend payments in this terrible financial year?
Which business structure or structures have the advantage of limited liability for equity investors?
Question 452 limited liability, expected and historical returns
What is the lowest and highest expected share price and expected return from owning shares in a company over a finite period of time?
Let the current share price be ##p_0##, the expected future share price be ##p_1##, the expected future dividend be ##d_1## and the expected return be ##r##. Define the expected return as:
##r=\dfrac{p_1-p_0+d_1}{p_0} ##
The answer choices are stated using inequalities. As an example, the first answer choice "(a) ##0≤p<∞## and ##0≤r< 1##", states that the share price must be larger than or equal to zero and less than positive infinity, and that the return must be larger than or equal to zero and less than one.
Question 542 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to double every 10 years, what must be the expected future capital return, given as an effective annual rate?
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 526 real and nominal returns and cash flows, inflation, no explanation
How can a nominal cash flow be precisely converted into a real cash flow?
Question 577 inflation, real and nominal returns and cash flows
What is the present value of a real payment of $500 in 2 years? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
The expression 'you have to spend money to make money' relates to which business decision?
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
Question 554 inflation, real and nominal returns and cash flows
On his 20th birthday, a man makes a resolution. He will put $30 cash under his bed at the end of every month starting from today. His birthday today is the first day of the month. So the first addition to his cash stash will be in one month. He will write in his will that when he dies the cash under the bed should be given to charity.
If the man lives for another 60 years, how much money will be under his bed if he dies just after making his last (720th) addition?
Also, what will be the real value of that cash in today's prices if inflation is expected to 2.5% pa? Assume that the inflation rate is an effective annual rate and is not expected to change.
The answers are given in the same order, the amount of money under his bed in 60 years, and the real value of that money in today's prices.
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
Question 574 inflation, real and nominal returns and cash flows, NPV
What is the present value of a nominal payment of $100 in 5 years? The real discount rate is 10% pa and the inflation rate is 3% pa.
Question 576 inflation, real and nominal returns and cash flows
What is the present value of a nominal payment of $1,000 in 4 years? The nominal discount rate is 8% pa and the inflation rate is 2% pa.
Question 604 inflation, real and nominal returns and cash flows
Apples and oranges currently cost $1 each. Inflation is 5% pa, and apples and oranges are equally affected by this inflation rate. Note that when payments are not specified as real, as in this question, they're conventionally assumed to be nominal.
Which of the following statements is NOT correct?
Question 664 real and nominal returns and cash flows, inflation, no explanation
What is the present value of real payments of $100 every year forever, with the first payment in one year? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Question 578 inflation, real and nominal returns and cash flows
Which of the following statements about inflation is NOT correct?
Question 522 income and capital returns, real and nominal returns and cash flows, inflation, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 2.5% pa. Inflation is expected to be 2.5% pa.
All of the above are effective nominal rates and investors believe that they will stay the same in perpetuity.
What are the property's expected real total, capital and income returns?
The answer choices below are given in the same order.
Suppose you had $100 in a savings account and the interest rate was 2% per year.
After 5 years, how much do you think you would have in the account if you left the money to grow?
Jan asks you for a loan. He wants $100 now and offers to pay you back $120 in 1 year. You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate.
Ignore credit risk. Remember:
### V_0 = \frac{V_t}{(1+r_\text{eff})^t} ###
Katya offers to pay you $10 at the end of every year for the next 5 years (t=1,2,3,4,5) if you pay her $50 now (t=0). You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate. Ignore credit risk.
For a price of $13, Carla will sell you a share paying a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $6, Carlos will sell you a share which will pay a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $102, Andrea will sell you a share which just paid a dividend of $10 yesterday, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##10(1+0.05)^1=$10.50## in one year from now, and the year after it will be ##10(1+0.05)^2=11.025## and so on.
The required return of the stock is 15% pa.
For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.
The required return of the stock is 15% pa.
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.
For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $100, Andrea will sell you a 2 year bond paying annual coupons of 10% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.
Question 22 NPV, perpetuity with growth, effective rate, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 10% given as an effective annual rate?
The first payment of $90 is in 3 years, followed by payments every 6 months in perpetuity after that which shrink by 3% every 6 months. That is, the growth rate every 6 months is actually negative 3%, given as an effective 6 month rate. So the payment at ## t=3.5 ## years will be ## 90(1-0.03)^1=87.3 ##, and so on.
Question 48 IRR, NPV, bond pricing, premium par and discount bonds, market efficiency
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What is the current price of the stock?
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
Question 335 foreign exchange rate, American and European terms
Investors expect Australia's central bank, the RBA, to reduce the policy rate at their next meeting due to fears that the economy is slowing. Then unexpectedly, the policy rate is actually kept unchanged.
What do you expect to happen to Australia's exchange rate?
High risk firms in danger of bankruptcy tend to have:
Question 213 income and capital returns, bond pricing, premium par and discount bonds
The coupon rate of a fixed annual-coupon bond is constant (always the same).
What can you say about the income return (##r_\text{income}##) of a fixed annual coupon bond? Remember that:
###r_\text{total} = r_\text{income} + r_\text{capital}###
###r_\text{total, 0 to 1} = \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0}###
Assume that there is no change in the bond's total annual yield to maturity from when it is issued to when it matures.
Select the most correct statement.
From its date of issue until maturity, the income return of a fixed annual coupon:
A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.
Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?
There are many ways to write the ordinary annuity formula.
Which of the following is NOT equal to the ordinary annuity formula?
This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
The following cash flows are expected:
- 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
- 1 payment of $400 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.
What is the net present value (NPV) of borrowing from your friend?
Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.
Some countries' interest rates are so low that they're zero.
If interest rates are 0% pa and are expected to stay at that level for the foreseeable future, what is the most that you would be prepared to pay a bank now if it offered to pay you $10 at the end of every year for the next 5 years?
In other words, what is the present value of five $10 payments at time 1, 2, 3, 4 and 5 if interest rates are 0% pa?
Discounted cash flow (DCF) valuation prices assets by finding the present value of the asset's future cash flows. The single cash flow, annuity, and perpetuity equations are very useful for this.
Which of the following equations is the 'perpetuity with growth' equation?
The first payment of a constant perpetual annual cash flow is received at time 5. Let this cash flow be ##C_5## and the required return be ##r##.
So there will be equal annual cash flows at time 5, 6, 7 and so on forever, and all of the cash flows will be equal so ##C_5 = C_6 = C_7 = ...##
When the perpetuity formula is used to value this stream of cash flows, it will give a value (V) at time:
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
The following is the Dividend Discount Model (DDM) used to price stocks:
###P_0=\dfrac{C_1}{r-g}###
If the assumptions of the DDM hold and the stock is fairly priced, which one of the following statements is NOT correct? The long term expected:
A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.
What is the implied growth rate of the dividend per year?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
In the dividend discount model:
###P_0 = \dfrac{C_1}{r-g}###
The return ##r## is supposed to be the:
Two years ago Fred bought a house for $300,000.
Now it's worth $500,000, based on recent similar sales in the area.
Fred's residential property has an expected total return of 8% pa.
He rents his house out for $2,000 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $23,173.86.
The future value of 12 months of rental payments one year ahead is $25,027.77.
What is the expected annual growth rate of the rental payments? In other words, by what percentage increase will Fred have to raise the monthly rent by each year to sustain the expected annual total return of 8%?
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
The following is the Dividend Discount Model (DDM) used to price stocks:
### P_0 = \frac{d_1}{r-g} ###Assume that the assumptions of the DDM hold and that the time period is measured in years.
Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###p_0=\frac{d_1}{r_\text{eff}-g_\text{eff}}###
Which expression is NOT equal to the expected capital return?
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.
What is the price of the share now?
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.
Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
Question 488 income and capital returns, payout policy, payout ratio, DDM
Two companies BigDiv and ZeroDiv are exactly the same except for their dividend payouts.
BigDiv pays large dividends and ZeroDiv doesn't pay any dividends.
Currently the two firms have the same earnings, assets, number of shares, share price, expected total return and risk.
Assume a perfect world with no taxes, no transaction costs, no asymmetric information and that all assets including business projects are fairly priced and therefore zero-NPV.
All things remaining equal, which of the following statements is NOT correct?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
A stock is expected to pay a dividend of $15 in one year (t=1), then $25 for 9 years after that (payments at t=2 ,3,...10), and on the 11th year (t=11) the dividend will be 2% less than at t=10, and will continue to shrink at the same rate every year after that forever. The required return of the stock is 10%. All rates are effective annual rates.
What is the price of the stock now?
A project to build a toll road will take 3 years to complete, costing three payments of $50 million, paid at the start of each year (at times 0, 1, and 2).
After completion, the toll road will yield a constant $10 million at the end of each year forever with no costs. So the first payment will be at t=4.
The required return of the project is 10% pa given as an effective nominal rate. All cash flows are nominal.
What is the payback period?
A three year project's NPV is negative. The cash flows of the project include a negative cash flow at the very start and positive cash flows over its short life. The required return of the project is 10% pa. Select the most correct statement.
A project has the following cash flows. Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $250 at time 2 is actually earned smoothly from t=1 to t=2:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 200 |
| 2 | 250 |
What is the payback period of the project in years?
A project's NPV is positive. Select the most correct statement:
A project has the following cash flows. Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $105 at time 2 is actually earned smoothly from t=1 to t=2:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -90 |
| 1 | 30 |
| 2 | 105 |
What is the payback period of the project in years?
A firm is considering a business project which costs $10m now and is expected to pay a single cash flow of $12.1m in two years.
Assume that the initial $10m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
A low-quality second-hand car can be bought now for $1,000 and will last for 1 year before it will be scrapped for nothing.
A high-quality second-hand car can be bought now for $4,900 and it will last for 5 years before it will be scrapped for nothing.
What is the equivalent annual cost of each car? Assume a discount rate of 10% pa, given as an effective annual rate.
The answer choices are given as the equivalent annual cost of the low-quality car and then the high quality car.
Question 180 equivalent annual cash flow, inflation, real and nominal returns and cash flows
Details of two different types of light bulbs are given below:
- Low-energy light bulbs cost $3.50, have a life of nine years, and use about $1.60 of electricity a year, paid at the end of each year.
- Conventional light bulbs cost only $0.50, but last only about a year and use about $6.60 of energy a year, paid at the end of each year.
The real discount rate is 5%, given as an effective annual rate. Assume that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the Equivalent Annual Cost (EAC) of the low-energy and conventional light bulbs. The below choices are listed in that order.
Carlos and Edwin are brothers and they both love Holden Commodore cars.
Carlos likes to buy the latest Holden Commodore car for $40,000 every 4 years as soon as the new model is released. As soon as he buys the new car, he sells the old one on the second hand car market for $20,000. Carlos never has to bother with paying for repairs since his cars are brand new.
Edwin also likes Commodores, but prefers to buy 4-year old cars for $20,000 and keep them for 11 years until the end of their life (new ones last for 15 years in total but the 4-year old ones only last for another 11 years). Then he sells the old car for $2,000 and buys another 4-year old second hand car, and so on.
Every time Edwin buys a second hand 4 year old car he immediately has to spend $1,000 on repairs, and then $1,000 every year after that for the next 10 years. So there are 11 payments in total from when the second hand car is bought at t=0 to the last payment at t=10. One year later (t=11) the old car is at the end of its total 15 year life and can be scrapped for $2,000.
Assuming that Carlos and Edwin maintain their love of Commodores and keep up their habits of buying new ones and second hand ones respectively, how much larger is Carlos' equivalent annual cost of car ownership compared with Edwin's?
The real discount rate is 10% pa. All cash flows are real and are expected to remain constant. Inflation is forecast to be 3% pa. All rates are effective annual. Ignore capital gains tax and tax savings from depreciation since cars are tax-exempt for individuals.
Question 215 equivalent annual cash flow, effective rate conversion
You're about to buy a car. These are the cash flows of the two different cars that you can buy:
- You can buy an old car for $5,000 now, for which you will have to buy $90 of fuel at the end of each week from the date of purchase. The old car will last for 3 years, at which point you will sell the old car for $500.
- Or you can buy a new car for $14,000 now for which you will have to buy $50 of fuel at the end of each week from the date of purchase. The new car will last for 4 years, at which point you will sell the new car for $1,000.
Bank interest rates are 10% pa, given as an effective annual rate. Assume that there are exactly 52 weeks in a year. Ignore taxes and environmental and pollution factors.
Should you buy the or the ?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Which firms tend to have high forward-looking price-earnings (PE) ratios?
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
You really want to go on a back packing trip to Europe when you finish university. Currently you have $1,500 in the bank. Bank interest rates are 8% pa, given as an APR compounding per month. If the holiday will cost $2,000, how long will it take for your bank account to reach that amount?
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
Your credit card shows a $600 debt liability. The interest rate is 24% pa, payable monthly. You can't pay any of the debt off, except in 6 months when it's your birthday and you'll receive $50 which you'll use to pay off the credit card. If that is your only repayment, how much will the credit card debt liability be one year from now?
You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.
How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.
A student just won the lottery. She won $1 million in cash after tax. She is trying to calculate how much she can spend per month for the rest of her life. She assumes that she will live for another 60 years. She wants to withdraw equal amounts at the beginning of every month, starting right now.
All of the cash is currently sitting in a bank account which pays interest at a rate of 6% pa, given as an APR compounding per month. On her last withdrawal, she intends to have nothing left in her bank account. How much can she withdraw at the beginning of each month?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
The phone company Telstra have 2 mobile service plans on offer which both have the same amount of phone call, text message and internet data credit. Both plans have a contract length of 24 months and the monthly cost is payable in advance. The only difference between the two plans is that one is a:
- 'Bring Your Own' (BYO) mobile service plan, costing $50 per month. There is no phone included in this plan. The other plan is a:
- 'Bundled' mobile service plan that comes with the latest smart phone, costing $71 per month. This plan includes the latest smart phone.
Neither plan has any additional payments at the start or end.
The only difference between the plans is the phone, so what is the implied cost of the phone as a present value?
Assume that the discount rate is 2% per month given as an effective monthly rate, the same high interest rate on credit cards.
In Australia, domestic university students are allowed to buy concession tickets for the bus, train and ferry which sell at a discount of 50% to full-price tickets.
The Australian Government do not allow international university students to buy concession tickets, they have to pay the full price.
Some international students see this as unfair and they are willing to pay for fake university identification cards which have the concession sticker.
What is the most that an international student would be willing to pay for a fake identification card?
Assume that international students:
- consider buying their fake card on the morning of the first day of university from their neighbour, just before they leave to take the train into university.
- buy their weekly train tickets on the morning of the first day of each week.
- ride the train to university and back home again every day seven days per week until summer holidays 40 weeks from now. The concession card only lasts for those 40 weeks. Assume that there are 52 weeks in the year for the purpose of interest rate conversion.
- a single full-priced one-way train ride costs $5.
- have a discount rate of 11% pa, given as an effective annual rate.
Approach this question from a purely financial view point, ignoring the illegality, embarrassment and the morality of committing fraud.
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
Question 535 DDM, real and nominal returns and cash flows, stock pricing
You are an equities analyst trying to value the equity of the Australian telecoms company Telstra, with ticker TLS. In Australia, listed companies like Telstra tend to pay dividends every 6 months. The payment around August is called the final dividend and the payment around February is called the interim dividend. Both occur annually.
- Today is mid-March 2015.
- TLS's last interim dividend of $0.15 was one month ago in mid-February 2015.
- TLS's last final dividend of $0.15 was seven months ago in mid-August 2014.
Judging by TLS's dividend history and prospects, you estimate that the nominal dividend growth rate will be 1% pa. Assume that TLS's total nominal cost of equity is 6% pa. The dividends are nominal cash flows and the inflation rate is 2.5% pa. All rates are quoted as nominal effective annual rates. Assume that each month is exactly one twelfth (1/12) of a year, so you can ignore the number of days in each month.
Calculate the current TLS share price.
An industrial chicken farmer grows chickens for their meat. Chickens:
- Cost $0.50 each to buy as chicks. They are bought on the day they’re born, at t=0.
- Grow at a rate of $0.70 worth of meat per chicken per week for the first 6 weeks (t=0 to t=6).
- Grow at a rate of $0.40 worth of meat per chicken per week for the next 4 weeks (t=6 to t=10) since they’re older and grow more slowly.
- Feed costs are $0.30 per chicken per week for their whole life. Chicken feed is bought and fed to the chickens once per week at the beginning of the week. So the first amount of feed bought for a chicken at t=0 costs $0.30, and so on.
- Can be slaughtered (killed for their meat) and sold at no cost at the end of the week. The price received for the chicken is their total value of meat (note that the chicken grows fast then slow, see above).
The required return of the chicken farm is 0.5% given as an effective weekly rate.
Ignore taxes and the fixed costs of the factory. Ignore the chicken’s welfare and other environmental and ethical concerns.
Find the equivalent weekly cash flow of slaughtering a chicken at 6 weeks and at 10 weeks so the farmer can figure out the best time to slaughter his chickens. The choices below are given in the same order, 6 and 10 weeks.
The boss of WorkingForTheManCorp has a wicked (and unethical) idea. He plans to pay his poor workers one week late so that he can get more interest on his cash in the bank.
Every week he is supposed to pay his 1,000 employees $1,000 each. So $1 million is paid to employees every week.
The boss was just about to pay his employees today, until he thought of this idea so he will actually pay them one week (7 days) later for the work they did last week and every week in the future, forever.
Bank interest rates are 10% pa, given as a real effective annual rate. So ##r_\text{eff annual, real} = 0.1## and the real effective weekly rate is therefore ##r_\text{eff weekly, real} = (1+0.1)^{1/52}-1 = 0.001834569##
All rates and cash flows are real, the inflation rate is 3% pa and there are 52 weeks per year. The boss will always pay wages one week late. The business will operate forever with constant real wages and the same number of employees.
What is the net present value (NPV) of the boss's decision to pay later?
Question 249 equivalent annual cash flow, effective rate conversion
Details of two different types of desserts or edible treats are given below:
- High-sugar treats like candy, chocolate and ice cream make a person very happy. High sugar treats are cheap at only $2 per day.
- Low-sugar treats like nuts, cheese and fruit make a person equally happy if these foods are of high quality. Low sugar treats are more expensive at $4 per day.
The advantage of low-sugar treats is that a person only needs to pay the dentist $2,000 for fillings and root canal therapy once every 15 years. Whereas with high-sugar treats, that treatment needs to be done every 5 years.
The real discount rate is 10%, given as an effective annual rate. Assume that there are 365 days in every year and that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the equivalent annual cash flow (EAC) of the high-sugar treats and low-sugar treats, including dental costs. The below choices are listed in that order.
Ignore the pain of dental therapy, personal preferences and other factors.
You just bought a nice dress which you plan to wear once per month on nights out. You bought it a moment ago for $600 (at t=0). In your experience, dresses used once per month last for 6 years.
Your younger sister is a student with no money and wants to borrow your dress once a month when she hits the town. With the increased use, your dress will only last for another 3 years rather than 6.
What is the present value of the cost of letting your sister use your current dress for the next 3 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new dress when your current one wears out; your sister will only use the current dress, not the next one that you will buy; and the price of a new dress never changes.
You own a nice suit which you wear once per week on nights out. You bought it one year ago for $600. In your experience, suits used once per week last for 6 years. So you expect yours to last for another 5 years.
Your younger brother said that retro is back in style so he wants to wants to borrow your suit once a week when he goes out. With the increased use, your suit will only last for another 4 years rather than 5.
What is the present value of the cost of letting your brother use your current suit for the next 4 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new suit when your current one wears out and your brother will not use the new one; your brother will only use your current suit so he will only use it for the next four years; and the price of a new suit never changes.
You own some nice shoes which you use once per week on date nights. You bought them 2 years ago for $500. In your experience, shoes used once per week last for 6 years. So you expect yours to last for another 4 years.
Your younger sister said that she wants to borrow your shoes once per week. With the increased use, your shoes will only last for another 2 years rather than 4.
What is the present value of the cost of letting your sister use your current shoes for the next 2 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new pair of shoes when your current pair wears out and your sister will not use the new ones; your sister will only use your current shoes so she will only use it for the next 2 years; and the price of new shoes never changes.
A stock is expected to pay its next dividend of $1 in one year. Future annual dividends are expected to grow by 2% pa. So the first dividend of $1 will be in one year, the year after that $1.02 (=1*(1+0.02)^1), and a year later $1.0404 (=1*(1+0.02)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
A stock just paid a dividend of $1. Future annual dividends are expected to grow by 2% pa. The next dividend of $1.02 (=1*(1+0.02)^1) will be in one year, and the year after that the dividend will be $1.0404 (=1*(1+0.02)^2), and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

A firm has a debt-to-assets ratio of 20%. What is its debt-to-equity ratio?
The 'time value of money' is most closely related to which of the following concepts?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_{0} = \frac{c_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What is the discount rate '## r_\text{eff} ##' in this equation?
A share was bought for $20 (at t=0) and paid its annual dividend of $3 one year later (at t=1). Just after the dividend was paid, the share price was $16 (at t=1). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
A share was bought for $10 (at t=0) and paid its annual dividend of $0.50 one year later (at t=1). Just after the dividend was paid, the share price was $11 (at t=1).
What was the total return, capital return and income return? Calculate your answers as effective annual rates. The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
A share was bought for $4 and paid an dividend of $0.50 one year later (at t=1 year).
Just after the dividend was paid, the share price fell to $3.50 (at t=1 year). What were the total return, capital return and income returns given as effective annual rates? The answer choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ## r_\text{income}##
A 90-day $1 million Bank Accepted Bill (BAB) was bought for $990,000 and sold 30 days later for $996,000 (at t=30 days).
What was the total return, capital return and income return over the 30 days it was held?
Despite the fact that money market instruments such as bills are normally quoted with simple interest rates, please calculate your answers as compound interest rates, specifically, as effective 30-day rates, which is how the below answer choices are listed.
##r_\text{total}##, ##r_\text{capital}##, ## r_\text{income}##
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 6.5 years from now (first payment at t=6.5).
- A single payment of $500 in 4 years and 3 months (t=4.25) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
The following cash flows are expected:
- Constant perpetual yearly payments of $70, with the first payment in 2.5 years from now (first payment at t=2.5).
- A single payment of $600 in 3 years and 9 months (t=3.75) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 523 income and capital returns, real and nominal returns and cash flows, inflation
A low-growth mature stock has an expected nominal total return of 6% pa and nominal capital return of 2% pa. Inflation is expected to be 3% pa.
All of the above are effective nominal rates and investors believe that they will stay the same in perpetuity.
What are the stock's expected real total, capital and income returns?
The answer choices below are given in the same order.
Total cash flows can be broken into income and capital cash flows.
What is the name given to the cash flow generated from selling shares at a higher price than they were bought?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume twice as much now (t=0) as in one year (t=1) and have nothing left in the bank at the end.
How much can you consume at time zero and one? The answer choices are given in the same order.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume half as much now (t=0) as in one year (t=1) and have nothing left in the bank at the end.
How much can you consume at time zero and one? The answer choices are given in the same order.
Question 536 idiom, bond pricing, capital structure, leverage
The expression 'my word is my bond' is often used in everyday language to make a serious promise.
Why do you think this expression uses the metaphor of a bond rather than a share?
Estimate the French bank Societe Generale's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that EUR is the euro, the European monetary union's currency.
- The 4 major European banks Credit Agricole (ACA), Deutsche Bank AG (DBK), UniCredit (UCG) and Banco Santander (SAN) are comparable companies to Societe Generale (GLE);
- Societe Generale's (GLE's) historical earnings per share (EPS) is EUR 2.92;
- ACA's backward-looking PE ratio is 16.29 and historical EPS is EUR 0.84;
- DBK's backward-looking PE ratio is 25.01 and historical EPS is EUR 1.26;
- SAN's backward-looking PE ratio is 14.71 and historical EPS is EUR 0.47;
- UCG's backward-looking PE ratio is 15.78 and historical EPS is EUR 0.40;
Note: Figures sourced from Google Finance on 27 March 2015.
Question 538 bond pricing, income and capital returns, no explanation
Risk-free government bonds that have coupon rates greater than their yields:
Which one of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Question 543 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to triple every 5 years, what must be the expected future capital return, given as an effective annual rate?
Question 548 equivalent annual cash flow, time calculation, no explanation
An Apple iPhone 6 smart phone can be bought now for $999. An Android Kogan Agora 4G+ smart phone can be bought now for $240.
If the Kogan phone lasts for one year, approximately how long must the Apple phone last for to have the same equivalent annual cost?
Assume that both phones have equivalent features besides their lifetimes, that both are worthless once they've outlasted their life, the discount rate is 10% pa given as an effective annual rate, and there are no extra costs or benefits from either phone.
Which of the following statements is NOT equivalent to the yield on debt?
Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
To your surprise, you can actually afford to pay $2,000 per month and your mortgage allows early repayments without fees. If you maintain these higher monthly payments, how long will it take to pay off your mortgage?
You just agreed to a 30 year fully amortising mortgage loan with monthly payments of $2,500. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change. The below choices are given in the same order.
You want to buy a house priced at $400,000. You have saved a deposit of $40,000. The bank has agreed to lend you $360,000 as a fully amortising loan with a term of 30 years. The interest rate is 8% pa payable monthly and is not expected to change.
What will be your monthly payments?
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
You want to buy an apartment worth $300,000. You have saved a deposit of $60,000.
The bank has agreed to lend you $240,000 as an interest only mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
A prospective home buyer can afford to pay $2,000 per month in mortgage loan repayments. The central bank recently lowered its policy rate by 0.25%, and residential home lenders cut their mortgage loan rates from 4.74% to 4.49%.
How much more can the prospective home buyer borrow now that interest rates are 4.49% rather than 4.74%? Give your answer as a proportional increase over the original amount he could borrow (##V_\text{before}##), so:
###\text{Proportional increase} = \frac{V_\text{after}-V_\text{before}}{V_\text{before}} ###Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates compounding per month.
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid annually. So there's only one coupon per year, paid in arrears every year.
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid semi-annually. So there are two coupons per year, paid in arrears every six months.
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
A two year Government bond has a face value of $100, a yield of 2.5% pa and a fixed coupon rate of 0.5% pa, paid semi-annually. What is its price?
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?
A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?
Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100), maturity (3 years) and yield (10%) as each other.
Which of the following statements is true?
A four year bond has a face value of $100, a yield of 6% and a fixed coupon rate of 12%, paid semi-annually. What is its price?
Which one of the following bonds is trading at a discount?
A firm wishes to raise $20 million now. They will issue 8% pa semi-annual coupon bonds that will mature in 5 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
A five year bond has a face value of $100, a yield of 12% and a fixed coupon rate of 6%, paid semi-annually.
What is the bond's price?
Which one of the following bonds is trading at par?
A firm wishes to raise $8 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
Which one of the following bonds is trading at a premium?
An investor bought two fixed-coupon bonds issued by the same company, a zero-coupon bond and a 7% pa semi-annual coupon bond. Both bonds have a face value of $1,000, mature in 10 years, and had a yield at the time of purchase of 8% pa.
A few years later, yields fell to 6% pa. Which of the following statements is correct? Note that a capital gain is an increase in price.
A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 8 years and have a face value of $1,000 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue? All numbers are rounded up.
A four year bond has a face value of $100, a yield of 9% and a fixed coupon rate of 6%, paid semi-annually. What is its price?
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
A 10 year bond has a face value of $100, a yield of 6% pa and a fixed coupon rate of 8% pa, paid semi-annually. What is its price?
Bonds X and Y are issued by the same company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X pays coupons of 6% pa and bond Y pays coupons of 8% pa. Which of the following statements is true?
A 30 year Japanese government bond was just issued at par with a yield of 1.7% pa. The fixed coupon payments are semi-annual. The bond has a face value of $100.
Six months later, just after the first coupon is paid, the yield of the bond increases to 2% pa. What is the bond's new price?
Bonds X and Y are issued by the same US company. Both bonds yield 6% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X pays coupons of 8% pa and bond Y pays coupons of 12% pa. Which of the following statements is true?
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 3 years from now (first payment at t=3).
- 1 payment of $600 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 727 inflation, real and nominal returns and cash flows
The Australian Federal Government lends money to domestic students to pay for their university education. This is known as the Higher Education Contribution Scheme (HECS). The nominal interest rate on the HECS loan is set equal to the consumer price index (CPI) inflation rate. The interest is capitalised every year, which means that the interest is added to the principal. The interest and principal does not need to be repaid by students until they finish study and begin working.
Which of the following statements about HECS loans is NOT correct?
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
Question 729 book and market values, balance sheet, no explanation
If a firm makes a profit and pays no dividends, which of the firm’s accounts will increase?
In the dividend discount model (DDM), share prices fall when dividends are paid. Let the high price before the fall be called the peak, and the low price after the fall be called the trough.
###P_0=\dfrac{C_1}{r-g}###
Which of the following statements about the DDM is NOT correct?
Question 734 real and nominal returns and cash flows, inflation, DDM, no explanation
An equities analyst is using the dividend discount model to price a company's shares. The company operates domestically and has no plans to expand overseas. It is part of a mature industry with stable positive growth prospects.
The analyst has estimated the real required return (r) of the stock and the value of the dividend that the stock just paid a moment before ##(C_\text{0 before})##.
What is the highest perpetual real growth rate of dividends (g) that can be justified? Select the most correct statement from the following choices. The highest perpetual real expected growth rate of dividends that can be justified is the country's expected:
Stocks in the United States usually pay quarterly dividends. For example, the software giant Microsoft paid a $0.23 dividend every quarter over the 2013 financial year and plans to pay a $0.28 dividend every quarter over the 2014 financial year.
Using the dividend discount model and net present value techniques, calculate the stock price of Microsoft assuming that:
- The time now is the beginning of July 2014. The next dividend of $0.28 will be received in 3 months (end of September 2014), with another 3 quarterly payments of $0.28 after this (end of December 2014, March 2015 and June 2015).
- The quarterly dividend will increase by 2.5% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in the financial year beginning in September 2015 will be $ 0.287 ##(=0.28×(1+0.025)^1)##, with the last at the end of June 2016. In the next financial year beginning in September 2016 each quarterly dividend will be $0.294175 ##(=0.28×(1+0.025)^2)##, with the last at the end of June 2017, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
Question 730 DDM, income and capital returns, no explanation
A stock’s current price is $1. Its expected total return is 10% pa and its long term expected capital return is 4% pa. It pays an annual dividend and the next one will be paid in one year. All rates are given as effective annual rates. The dividend discount model is thought to be a suitable model for the stock. Ignore taxes. Which of the following statements about the stock is NOT correct?
A share’s current price is $60. It’s expected to pay a dividend of $1.50 in one year. The growth rate of the dividend is 0.5% pa and the stock’s required total return is 3% pa. The stock’s price can be modeled using the dividend discount model (DDM):
##P_0=\dfrac{C_1}{r-g}##
Which of the following methods is NOT equal to the stock’s expected price in one year and six months (t=1.5 years)? Note that the symbolic formulas shown in each line below do equal the formulas with numbers. The formula is just repeated with symbols and then numbers in case it helps you to identify the incorrect statement more quickly.
Question 210 real estate, inflation, real and nominal returns and cash flows, income and capital returns
Assume that the Gordon Growth Model (same as the dividend discount model or perpetuity with growth formula) is an appropriate method to value real estate.
An old rule of thumb in the real estate industry is that properties should yield a 5% pa rental return. Some investors also regard property to be as risky as the stock market, therefore property is thought to have a required total return of 9% pa which is the average total return on the stock market including dividends.
Assume that all returns are effective annual rates and they are nominal (not reduced by inflation). Inflation is expected to be 2% pa.
You're considering purchasing an investment property which has a rental yield of 5% pa and you expect it to have the same risk as the stock market. Select the most correct statement about this property.
Question 529 DDM, real and nominal returns and cash flows, inflation, real estate, no explanation
If housing rents are constrained from growing more than the maximum target inflation rate, and houses can be priced as a perpetuity of growing net rental cash flows, then what is the implication for house prices, all things remaining equal? Select the most correct answer.
Background: Since 1990, many central banks across the world have become 'inflation targeters'. They have adopted a policy of trying to keep inflation in a predictable narrow range, with the hope of encouraging long-term lending to fund more investment and maintain higher GDP growth.
Australia's central bank, the Reserve Bank of Australia (RBA), has specifically stated their inflation target range is between 2 and 3% pa.
Some Australian residential property market commentators suggest that because rental costs comprise a large part of the Australian consumer price index (CPI), rent costs across the nation cannot significantly exceed the maximum inflation target range of 3% pa without the prices of other goods growing by less than the target range for long periods, which is unlikely.
A 2 year government bond yields 5% pa with a coupon rate of 6% pa, paid semi-annually.
Find the effective six month rate, effective annual rate and the effective daily rate. Assume that each month has 30 days and that there are 360 days in a year.
All answers are given in the same order:
##r_\text{eff semi-annual}##, ##r_\text{eff yrly}##, ##r_\text{eff daily}##.
A home loan company advertises an interest rate of 6% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A credit card company advertises an interest rate of 18% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A semi-annual coupon bond has a yield of 3% pa. Which of the following statements about the yield is NOT correct? All rates are given to four decimal places.
Question 659 APR, effective rate, effective rate conversion, no explanation
A home loan company advertises an interest rate of 9% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given with an accuracy of 4 decimal places.
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###You just entered into a fully amortising home loan with a principal of $600,000, a variable interest rate of 4.25% pa and a term of 25 years.
Immediately after settling the loan, the variable interest rate suddenly falls to 4% pa! You can't believe your luck. Despite this, you plan to continue paying the same home loan payments as you did before. How long will it now take to pay off your home loan?
Assume that the lower interest rate was granted immediately and that rates were and are now again expected to remain constant. Round your answer up to the nearest whole month.
Many Australian home loans that are interest-only actually require payments to be made on a fully amortising basis after a number of years.
You decide to borrow $600,000 from the bank at an interest rate of 4.25% pa for 25 years. The payments will be interest-only for the first 10 years (t=0 to 10 years), then they will have to be paid on a fully amortising basis for the last 15 years (t=10 to 25 years).
Assuming that interest rates will remain constant, what will be your monthly payments over the first 10 years from now, and then the next 15 years after that? The answer options are given in the same order.
You're trying to save enough money for a deposit to buy a house. You want to buy a house worth $400,000 and the bank requires a 20% deposit ($80,000) before it will give you a loan for the other $320,000 that you need.
You currently have no savings, but you just started working and can save $2,000 per month, with the first payment in one month from now. Bank interest rates on savings accounts are 4.8% pa with interest paid monthly and interest rates are not expected to change.
How long will it take to save the $80,000 deposit? Round your answer up to the nearest month.
Question 662 APR, effective rate, effective rate conversion, no explanation
Which of the following interest rate labels does NOT make sense?
Question 405 DDM, income and capital returns, no explanation
The perpetuity with growth formula is:
###P_0= \dfrac{C_1}{r-g}###
Which of the following is NOT equal to the total required return (r)?
For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.
The required return of the stock is 10% pa.
A fairly valued share's current price is $4 and it has a total required return of 30%. Dividends are paid annually and next year's dividend is expected to be $1. After that, dividends are expected to grow by 5% pa in perpetuity. All rates are effective annual returns.
What is the expected dividend income paid at the end of the second year (t=2) and what is the expected capital gain from just after the first dividend (t=1) to just after the second dividend (t=2)? The answers are given in the same order, the dividend and then the capital gain.
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Question 157 bill pricing, simple interest rate, no explanation
A 90-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 6% pa and there are 365 days in the year. What is its price?
A 180-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A 90-day Bank Accepted Bill (BAB) has a face value of $1,000,000. The simple interest rate is 10% pa and there are 365 days in the year. What is its price now?
Question 147 bill pricing, simple interest rate, no explanation
A 30-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A 60-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A 30-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 2.5% pa and there are 365 days in the year. What is its price now?
Question 327 bill pricing, simple interest rate, no explanation
On 27/09/13, three month Swiss government bills traded at a yield of -0.2%, given as a simple annual yield. That is, interest rates were negative.
If the face value of one of these 90 day bills is CHF1,000,000 (CHF represents Swiss Francs, the Swiss currency), what is the price of one of these bills?
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
A young lady is trying to decide if she should attend university or not.
The young lady's parents say that she must attend university because otherwise all of her hard work studying and attending school during her childhood was a waste.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The hard work studying at school in her childhood should be classified as:
A young lady is trying to decide if she should attend university. Her friends say that she should go to university because she is more likely to meet a clever young man than if she begins full time work straight away.
What's the correct way to classify this item from a capital budgeting perspective when trying to find the Net Present Value of going to university rather than working?
The opportunity to meet a desirable future spouse should be classified as:
A man is thinking about taking a day off from his casual painting job to relax.
He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.
But he's thinking about the hours that he could work today (in the future) which are:
A man has taken a day off from his casual painting job to relax.
It's the end of the day and he's thinking about the hours that he could have spent working (in the past) which are now:
What is the net present value (NPV) of undertaking a full-time Australian undergraduate business degree as an Australian citizen? Only include the cash flows over the duration of the degree, ignore any benefits or costs of the degree after it's completed.
Assume the following:
- The degree takes 3 years to complete and all students pass all subjects.
- There are 2 semesters per year and 4 subjects per semester.
- University fees per subject per semester are $1,277, paid at the start of each semester. Fees are expected to remain constant in real terms for the next 3 years.
- There are 52 weeks per year.
- The first semester is just about to start (t=0). The first semester lasts for 19 weeks (t=0 to 19).
- The second semester starts immediately afterwards (t=19) and lasts for another 19 weeks (t=19 to 38).
- The summer holidays begin after the second semester ends and last for 14 weeks (t=38 to 52). Then the first semester begins the next year, and so on.
- Working full time at the grocery store instead of studying full-time pays $20/hr and you can work 35 hours per week. Wages are paid at the end of each week and are expected to remain constant in real terms.
- Full-time students can work full-time during the summer holiday at the grocery store for the same rate of $20/hr for 35 hours per week.
- The discount rate is 9.8% pa. All rates and cash flows are real. Inflation is expected to be 3% pa. All rates are effective annual.
The NPV of costs from undertaking the university degree is:
Find the cash flow from assets (CFFA) of the following project.
| One Year Mining Project Data | ||
| Project life | 1 year | |
| Initial investment in building mine and equipment | $9m | |
| Depreciation of mine and equipment over the year | $8m | |
| Kilograms of gold mined at end of year | 1,000 | |
| Sale price per kilogram | $0.05m | |
| Variable cost per kilogram | $0.03m | |
| Before-tax cost of closing mine at end of year | $4m | |
| Tax rate | 30% | |
Note 1: Due to the project, the firm also anticipates finding some rare diamonds which will give before-tax revenues of $1m at the end of the year.
Note 2: The land that will be mined actually has thermal springs and a family of koalas that could be sold to an eco-tourist resort for an after-tax amount of $3m right now. However, if the mine goes ahead then this natural beauty will be destroyed.
Note 3: The mining equipment will have a book value of $1m at the end of the year for tax purposes. However, the equipment is expected to fetch $2.5m when it is sold.
Find the project's CFFA at time zero and one. Answers are given in millions of dollars ($m), with the first cash flow at time zero, and the second at time one.
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
Question 524 risk, expected and historical returns, bankruptcy or insolvency, capital structure, corporate financial decision theory, limited liability
Which of the following statements is NOT correct?
When using the dividend discount model to price a stock:
### p_{0} = \frac{d_1}{r - g} ###
The growth rate of dividends (g):
The following is the Dividend Discount Model used to price stocks:
### p_0=\frac{d_1}{r-g} ###
Which of the following statements about the Dividend Discount Model is NOT correct?
Question 415 income and capital returns, real estate, no explanation
You just bought a residential apartment as an investment property for $500,000.
You intend to rent it out to tenants. They are ready to move in, they would just like to know how much the monthly rental payments will be, then they will sign a twelve-month lease.
You require a total return of 8% pa and a rental yield of 5% pa.
What would the monthly paid-in-advance rental payments have to be this year to receive that 5% annual rental yield?
Also, if monthly rental payments can be increased each year when a new lease agreement is signed, by how much must you increase rents per year to realise the 8% pa total return on the property?
Ignore all taxes and the costs of renting such as maintenance costs, real estate agent fees, utilities and so on. Assume that there will be no periods of vacancy and that tenants will promptly pay the rental prices you charge.
Note that the first rental payment will be received at t=0. The first lease agreement specifies the first 12 equal payments from t=0 to 11. The next lease agreement can have a rental increase, so the next twelve equal payments from t=12 to 23 can be higher than previously, and so on forever.
You are promised 20 payments of $100, where the first payment is immediate (t=0) and the last is at the end of the 19th year (t=19). The effective annual discount rate is ##r##.
Which of the following equations does NOT give the correct present value of these 20 payments?
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Which of the following interest rate quotes is NOT equivalent to a 10% effective annual rate of return? Assume that each year has 12 months, each month has 30 days, each day has 24 hours, each hour has 60 minutes and each minute has 60 seconds. APR stands for Annualised Percentage Rate.
Question 547 PE ratio, Multiples valuation, DDM, income and capital returns, no explanation
A firm pays out all of its earnings as dividends. Because of this, the firm has no real growth in earnings, dividends or stock price since there is no re-investment back into the firm to buy new assets and make higher earnings. The dividend discount model is suitable to value this company.
The firm's revenues and costs are expected to increase by inflation in the foreseeable future. The firm has no debt. It operates in the services industry and has few physical assets so there is negligible depreciation expense and negligible net working capital required.
Which of the following statements about this firm's PE ratio is NOT correct? The PE ratio should:
Note: The inverse of x is 1/x.
A company announces that it will pay a dividend, as the market expected. The company's shares trade on the stock exchange which is open from 10am in the morning to 4pm in the afternoon each weekday. When would the share price be expected to fall by the amount of the dividend? Ignore taxes.
The share price is expected to fall during the:
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
Three years ago Frederika bought a house for $400,000.
Now it's worth $600,000, based on recent similar sales in the area.
Frederika's residential property has an expected total return of 7% pa.
She rents her house out for $2,500 per month, paid in advance. Every 12 months she plans to increase the rental payments.
The present value of 12 months of rental payments is $29,089.48.
The future value of 12 months of rental payments one year ahead is $31,125.74.
What is the expected annual capital yield of the property?
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use earnings before interest and tax (EBIT).
###\begin{aligned} FFCF &= (EBIT)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ \end{aligned} \\###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use net operating profit after tax (NOPAT).
###\begin{aligned} FFCF &= NOPAT + Depr - CapEx -\Delta NWC \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC \\ \end{aligned} \\###
Question 413 CFFA, interest tax shield, depreciation tax shield
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA).
One method is to use the following formulas to transform net income (NI) into FFCF including interest and depreciation tax shields:
###FFCF=NI + Depr - CapEx -ΔNWC + IntExp###
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )###
Another popular method is to use EBITDA rather than net income. EBITDA is defined as:
###EBITDA=Rev - COGS - FC###
One of the below formulas correctly calculates FFCF from EBITDA, including interest and depreciation tax shields, giving an identical answer to that above. Which formula is correct?
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| UniBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 80 | |
| COGS | 40 | |
| Operating expense | 15 | |
| Depreciation | 10 | |
| Interest expense | 5 | |
| Income before tax | 10 | |
| Tax at 30% | 3 | |
| Net income | 7 | |
| UniBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 90 |
| PPE | ||
| Cost | 360 | 320 |
| Accumul. depr. | 40 | 30 |
| Carrying amount | 320 | 290 |
| Total assets | 440 | 380 |
| Liabilities | ||
| Current liabilities | 110 | 60 |
| Non-current liabilities | 190 | 180 |
| Owners' equity | ||
| Retained earnings | 95 | 95 |
| Contributed equity | 45 | 45 |
| Total L and OE | 440 | 380 |
Note: all figures are given in millions of dollars ($m).
Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Piano Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 310 | |
| COGS | 185 | |
| Operating expense | 20 | |
| Depreciation | 15 | |
| Interest expense | 10 | |
| Income before tax | 80 | |
| Tax at 30% | 24 | |
| Net income | 56 | |
| Piano Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 240 | 230 |
| PPE | ||
| Cost | 420 | 400 |
| Accumul. depr. | 50 | 35 |
| Carrying amount | 370 | 365 |
| Total assets | 610 | 595 |
| Liabilities | ||
| Current liabilities | 180 | 190 |
| Non-current liabilities | 290 | 265 |
| Owners' equity | ||
| Retained earnings | 90 | 90 |
| Contributed equity | 50 | 50 |
| Total L and OE | 610 | 595 |
Note: all figures are given in millions of dollars ($m).
A firm has a debt-to-equity ratio of 25%. What is its debt-to-assets ratio?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of equity to raise money for new projects of similar systematic risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.
Which of the below FFCF formulas include the interest tax shield in the cash flow?
###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
A firm's weighted average cost of capital before tax (##r_\text{WACC before tax}##) would increase due to:
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
A company has:
- 140 million shares outstanding.
- The market price of one share is currently $2.
- The company's debentures are publicly traded and their market price is equal to 93% of the face value.
- The debentures have a total face value of $50,000,000 and the current yield to maturity of corporate debentures is 12% per annum.
- The risk-free rate is 8.50% and the market return is 13.7%.
- Market analysts estimated that the company's stock has a beta of 0.90.
- The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC) in a classical tax system?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A company has:
- 10 million common shares outstanding, each trading at a price of $90.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant dividend of 9% of par. They currently trade at a price of $120 each.
- Debentures that have a total face value of $60,000,000 and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 90% of their face value.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts estimate that the company's common stock has a beta of 1.2. The corporate tax rate is 30%.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A company has:
- 100 million ordinary shares outstanding which are trading at a price of $5 each. Market analysts estimated that the company's ordinary stock has a beta of 1.5. The risk-free rate is 5% and the market return is 10%.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant annual dividend of 9% of par. The next dividend will be paid in one year. Assume that all preference dividends will be paid when promised. They currently trade at a price of $90 each.
- Debentures that have a total face value of $200 million and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 110% of their face value.
The corporate tax rate is 30%. All returns and yields are given as effective annual rates.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
Question 418 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $8m | |
| Depreciation of equipment per year | $8m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 4m | |
| Sale price per unit | $10 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense in first year (at t=1) | $0.562m | |
| Corporate tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 9% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.32 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-equity ratio | 50% | |
Notes
- Due to the project, current assets will increase by $6m now (t=0) and fall by $6m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa. All rates are given as effective annual rates.
- The project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Question 419 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM, no explanation
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $6m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 9m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $6 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense in first year (at t=1) | $0.53m | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.08 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-assets ratio | 50% | |
Notes
- Due to the project, current assets will increase by $5m now (t=0) and fall by $5m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-assets ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Question 691 continuously compounding rate, effective rate, continuously compounding rate conversion, no explanation
A bank quotes an interest rate of 6% pa with quarterly compounding. Note that another way of stating this rate is that it is an annual percentage rate (APR) compounding discretely every 3 months.
Which of the following statements about this rate is NOT correct? All percentages are given to 6 decimal places. The equivalent:
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 2 | 2 | 2 | 10 | 3 | ... |
After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What is the current price of the stock?
Question 218 NPV, IRR, profitability index, average accounting return
Which of the following statements is NOT correct?
You deposit money into a bank. Which of the following statements is NOT correct? You:
You bought a house, primarily funded using a home loan from a bank. Which of the following statements is NOT correct?
Question 737 financial statement, balance sheet, income statement
Where can a publicly listed firm's book value of equity be found? It can be sourced from the company's:
Question 740 real and nominal returns and cash flows, DDM, inflation
Taking inflation into account when using the DDM can be hard. Which of the following formulas will NOT give a company's current stock price ##(P_0)##? Assume that the annual dividend was just paid ##(C_0)##, and the next dividend will be paid in one year ##(C_1)##.
A home loan company advertises an interest rate of 4.5% pa, payable monthly. Which of the following statements about the interest rate is NOT correct?
Question 742 price gains and returns over time, no explanation
For an asset's price to quintuple (be five times as big, say from $1 to $5) every 5 years, what must be its effective annual capital return?
Question 743 price gains and returns over time, no explanation
How many years will it take for an asset's price to triple (increase from say $1 to $3) if it grows by 5% pa?
Question 744 income and capital returns, real and nominal returns and cash flows, inflation
If someone says "my shares rose by 10% last year", what do you assume that they mean? The effective annual:
Question 745 real and nominal returns and cash flows, inflation, income and capital returns
If the nominal gold price is expected to increase at the same rate as inflation which is 3% pa, which of the following statements is NOT correct?
A stock is expected to pay a dividend of $1 in one year. Its future annual dividends are expected to grow by 10% pa. So the first dividend of $1 is in one year, and the year after that the dividend will be $1.1 (=1*(1+0.1)^1), and a year later $1.21 (=1*(1+0.1)^2) and so on forever.
Its required total return is 30% pa. The total required return and growth rate of dividends are given as effective annual rates. The stock is fairly priced.
Calculate the pay back period of buying the stock and holding onto it forever, assuming that the dividends are received as at each time, not smoothly over each year.
Question 748 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $2 tonight if you buy it today.
Thereafter the annual dividend is expected to grow by 3% pa, so the next dividend after the $2 one tonight will be $2.06 in one year, then in two years it will be $2.1218 and so on. The stock's required return is 8% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
A share will pay its next dividend of ##C_1## in one year, and will continue to pay a dividend every year after that forever, growing at a rate of ##g##. So the next dividend will be ##C_2=C_1 (1+g)^1##, then ##C_3=C_2 (1+g)^1##, and so on forever.
The current price of the share is ##P_0## and its required return is ##r##
Which of the following is NOT equal to the expected share price in 2 years ##(P_2)## just after the dividend at that time ##(C_2)## has been paid?
Itau Unibanco is a major listed bank in Brazil with a market capitalisation of equity equal to BRL 85.744 billion, EPS of BRL 3.96 and 2.97 billion shares on issue.
Banco Bradesco is another major bank with total earnings of BRL 8.77 billion and 2.52 billion shares on issue.
Estimate Banco Bradesco's current share price using a price-earnings multiples approach assuming that Itau Unibanco is a comparable firm.
Note that BRL is the Brazilian Real, their currency. Figures sourced from Google Finance on the market close of the BVMF on 24 July 2015.
Telsa Motors advertises that its Model S electric car saves $570 per month in fuel costs. Assume that Tesla cars last for 10 years, fuel and electricity costs remain the same, and savings are made at the end of each month with the first saving of $570 in one month from now.
The effective annual interest rate is 15.8%, and the effective monthly interest rate is 1.23%. What is the present value of the savings?
The following cash flows are expected:
- A perpetuity of yearly payments of $30, with the first payment in 5 years (first payment at t=5, which continues every year after that forever).
- One payment of $100 in 6 years and 3 months (t=6.25).
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 4% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###A firm wishes to raise $50 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 6 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
A firm wishes to raise $50 million now. They will issue 5% pa semi-annual coupon bonds that will mature in 3 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
A firm wishes to raise $50 million now. They will issue 5% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
Question 758 time calculation, fully amortising loan, no explanation
Two years ago you entered into a fully amortising home loan with a principal of $1,000,000, an interest rate of 6% pa compounding monthly with a term of 25 years.
Then interest rates suddenly fall to 4.5% pa (t=0), but you continue to pay the same monthly home loan payments as you did before. How long will it now take to pay off your home loan? Measure the time taken to pay off the home loan from the current time which is 2 years after the home loan was first entered into.
Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 2, which was the 24th payment since the loan was granted. Also assume that rates were and are expected to remain constant.
Question 759 time calculation, fully amortising loan, no explanation
Five years ago you entered into a fully amortising home loan with a principal of $500,000, an interest rate of 4.5% pa compounding monthly with a term of 25 years.
Then interest rates suddenly fall to 3% pa (t=0), but you continue to pay the same monthly home loan payments as you did before. How long will it now take to pay off your home loan? Measure the time taken to pay off the home loan from the current time which is 5 years after the home loan was first entered into.
Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 5, which was the 60th payment since the loan was granted. Also assume that rates were and are expected to remain constant.
The phone company Optus have 2 mobile service plans on offer which both have the same amount of phone call, text message and internet data credit. Both plans have a contract length of 24 months and the monthly cost is payable in advance. The only difference between the two plans is that one is a:
- 'Bring Your Own' (BYO) mobile service plan, costing $80 per month. There is no phone included in this plan. The other plan is a:
- 'Bundled' mobile service plan that comes with the latest smart phone, costing $100 per month. This plan includes the latest smart phone.
Neither plan has any additional payments at the start or end. Assume that the discount rate is 1% per month given as an effective monthly rate.
The only difference between the plans is the phone, so what is the implied cost of the phone as a present value? Given that the latest smart phone actually costs $600 to purchase outright from another retailer, should you commit to the BYO plan or the bundled plan?
A stock is expected to pay its first dividend of $20 in 3 years (t=3), which it will continue to pay for the next nine years, so there will be ten $20 payments altogether with the last payment in year 12 (t=12).
From the thirteenth year onward, the dividend is expected to be 4% more than the previous year, forever. So the dividend in the thirteenth year (t=13) will be $20.80, then $21.632 in year 14, and so on forever. The required return of the stock is 10% pa. All rates are effective annual rates. Calculate the current (t=0) stock price.
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
An investor bought a 5 year government bond with a 2% pa coupon rate at par. Coupons are paid semi-annually. The face value is $100.
Calculate the bond's new price 8 months later after yields have increased to 3% pa. Note that both yields are given as APR's compounding semi-annually. Assume that the yield curve was flat before the change in yields, and remained flat afterwards as well.
A 4.5% fixed coupon Australian Government bond was issued at par in mid-April 2009. Coupons are paid semi-annually in arrears in mid-April and mid-October each year. The face value is $1,000. The bond will mature in mid-April 2020, so the bond had an original tenor of 11 years.
Today is mid-September 2015 and similar bonds now yield 1.9% pa.
What is the bond's new price? Note: there are 10 semi-annual coupon payments remaining from now (mid-September 2015) until maturity (mid-April 2020); both yields are given as APR's compounding semi-annually; assume that the yield curve was flat before the change in yields, and remained flat afterwards as well.
Question 739 real and nominal returns and cash flows, inflation
There are a number of different formulas involving real and nominal returns and cash flows. Which one of the following formulas is NOT correct? All returns are effective annual rates. Note that the symbol ##\approx## means 'approximately equal to'.
Which of the following companies is most suitable for valuation using PE multiples techniques?
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.

What was MSFT's backwards-looking price-earnings ratio?
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.

What was CBA's backwards-looking price-earnings ratio?
A firm has 1 million shares which trade at a price of $30 each. The firm is expected to announce earnings of $3 million at the end of the year and pay an annual dividend of $1.50 per share.
What is the firm's (forward looking) price/earnings (PE) ratio?
A mature firm has constant expected future earnings and dividends. Both amounts are equal. So earnings and dividends are expected to be equal and unchanging.
Which of the following statements is NOT correct?
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
Below are some statements about loans and bonds. The first descriptive sentence is correct. But one of the second sentences about the loans' or bonds' prices is not correct. Which statement is NOT correct? Assume that interest rates are positive.
Note that coupons or interest payments are the periodic payments made throughout a bond or loan's life. The face or par value of a bond or loan is the amount paid at the end when the debt matures.
Question 143 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 6-month zero coupon bond at a yield of 6% pa, and
- A 12 month zero coupon bond at a yield of 7% pa.
What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Find the cash flow from assets (CFFA) of the following project.
| Project Data | |
| Project life | 2 years |
| Initial investment in equipment | $8m |
| Depreciation of equipment per year for tax purposes | $3m |
| Unit sales per year | 10m |
| Sale price per unit | $9 |
| Variable cost per unit | $4 |
| Fixed costs per year, paid at the end of each year | $2m |
| Tax rate | 30% |
Note 1: Due to the project, the firm will have to purchase $40m of inventory initially (at t=0). Half of this inventory will be sold at t=1 and the other half at t=2.
Note 2: The equipment will have a book value of $2m at the end of the project for tax purposes. However, the equipment is expected to fetch $1m when it is sold. Assume that the full capital loss is tax-deductible and taxed at the full corporate tax rate.
Note 3: The project will be fully funded by equity which investors will expect to pay dividends totaling $10m at the end of each year.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
The hardest and most important aspect of business project valuation is the estimation of the:
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
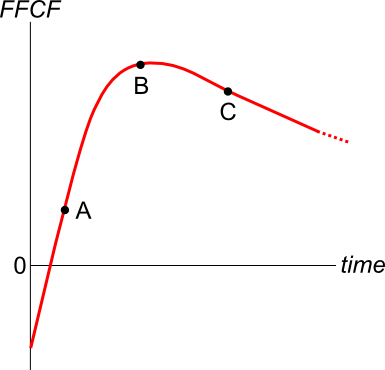
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
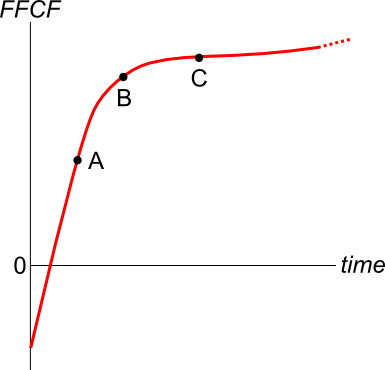
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the balance sheet needed? Note that the balance sheet is sometimes also called the statement of financial position.
An effective semi-annual return of 5% ##(r_\text{eff 6mth})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
An effective monthly return of 1% ##(r_\text{eff monthly})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
Question 657 systematic and idiosyncratic risk, CAPM, no explanation
A stock's required total return will decrease when its:
Question 711 continuously compounding rate, continuously compounding rate conversion
A continuously compounded semi-annual return of 5% ##(r_\text{cc 6mth})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
Question 710 continuously compounding rate, continuously compounding rate conversion
A continuously compounded monthly return of 1% ##(r_\text{cc monthly})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
Question 708 continuously compounding rate, continuously compounding rate conversion
Convert a 10% continuously compounded annual rate ##(r_\text{cc annual})## into an effective annual rate ##(r_\text{eff annual})##. The equivalent effective annual rate is:
Question 707 continuously compounding rate, continuously compounding rate conversion
Convert a 10% effective annual rate ##(r_\text{eff annual})## into a continuously compounded annual rate ##(r_\text{cc annual})##. The equivalent continuously compounded annual rate is:
Question 658 CFFA, income statement, balance sheet, no explanation
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the income statement needed? Note that the income statement is sometimes also called the profit and loss, P&L, or statement of financial performance.
In 2014 the median starting salaries of male and female Australian bachelor degree accounting graduates aged less than 25 years in their first full-time industry job was $50,000 before tax, according to Graduate Careers Australia. See page 9 of this report. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below.
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $50,000 per annum before-tax?
A $100 stock has a continuously compounded expected total return of 10% pa. Its dividend yield is 2% pa with continuous compounding. What do you expect its price to be in one year?
A stock's required total return will increase when its:
The average weekly earnings of an Australian adult worker before tax was $1,542.40 per week in November 2014 according to the Australian Bureau of Statistics. Therefore average annual earnings before tax were $80,204.80 assuming 52 weeks per year. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below:
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $80,204.80 per annum before-tax?
An American wishes to convert USD 1 million to Australian dollars (AUD). The exchange rate is 0.8 USD per AUD. How much is the USD 1 million worth in AUD?
An Indonesian lady wishes to convert 1 million Indonesian rupiah (IDR) to Australian dollars (AUD). Exchange rates are 13,125 IDR per USD and 0.79 USD per AUD. How many AUD is the IDR 1 million worth?
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 6% pa.
- Stock A has an expected return of 5% pa.
- Stock B has an expected return of 10% pa.
What portfolio weights should the investor have in stocks A and B respectively?
An investor bought a 20 year 5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly rose to 5.5% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
Question 345 capital budgeting, break even, NPV
| Project Data | ||
| Project life | 10 yrs | |
| Initial investment in factory | $10m | |
| Depreciation of factory per year | $1m | |
| Expected scrap value of factory at end of project | $0 | |
| Sale price per unit | $10 | |
| Variable cost per unit | $6 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense per year | 0 | |
| Tax rate | 30% | |
| Cost of capital per annum | 10% | |
Notes
- The firm's current liabilities are forecast to stay at $0.5m. The firm's current assets (mostly inventory) is currently $1m, but is forecast to grow by $0.1m at the end of each year due to the project.
At the end of the project, the current assets accumulated due to the project can be sold for the same price that they were bought. - A marketing survey was used to forecast sales. It cost $1.4m which was just paid. The cost has been capitalised by the accountants and is tax-deductible over the life of the project, regardless of whether the project goes ahead or not. This amortisation expense is not included in the depreciation expense listed in the table above.
Assumptions
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 3% pa.
- All rates are given as effective annual rates.
Find the break even unit production (Q) per year to achieve a zero Net Income (NI) and Net Present Value (NPV), respectively. The answers below are listed in the same order.
A pharmaceutical firm has just discovered a valuable new drug. So far the news has been kept a secret.
The net present value of making and commercialising the drug is $200 million, but $600 million of bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and bond raising to shareholders simultaneously in the same announcement. The bonds will be issued shortly after.
Once the announcement is made and the bonds are issued, what is the expected increase in the value of the firm's assets (ΔV), market capitalisation of debt (ΔD) and market cap of equity (ΔE)?
The triangle symbol is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##ΔV = ΔD+ΔE##
The CAPM can be used to find a business's expected opportunity cost of capital:
###r_i=r_f+β_i (r_m-r_f)###
What should be used as the risk free rate ##r_f##?
A mining firm has just discovered a new mine. So far the news has been kept a secret.
The net present value of digging the mine and selling the minerals is $250 million, but $500 million of new equity and $300 million of new bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and equity and bond raising to shareholders simultaneously in the same announcement. The shares and bonds will be issued shortly after.
Once the announcement is made and the new shares and bonds are issued, what is the expected increase in the value of the firm's assets ##(\Delta V)##, market capitalisation of debt ##(\Delta D)## and market cap of equity ##(\Delta E)##? Assume that markets are semi-strong form efficient.
The triangle symbol ##\Delta## is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##\Delta V = \Delta D+ \Delta E##
A young lady is trying to decide if she should attend university or begin working straight away in her home town.
The young lady's grandma says that she should not go to university because she is less likely to marry the local village boy whom she likes because she will spend less time with him if she attends university.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The cost of not marrying the local village boy should be classified as:
A project's net present value (NPV) is negative. Select the most correct statement.
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
The required return on the project is 10%, given as an effective annual rate.
What is the Internal Rate of Return (IRR) of this project? The following choices are effective annual rates. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What type of present value equation is best suited to value a residential house investment property that is expected to pay constant rental payments forever? Note that 'constant' has the same meaning as 'level' in this context.
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Note that a fair gamble is a bet that has an expected value of zero, such as paying $0.50 to win $1 in a coin flip with heads or nothing if it lands tails. Fairly priced insurance is when the expected present value of the insurance premiums is equal to the expected loss from the disaster that the insurance protects against, such as the cost of rebuilding a home after a catastrophic fire.
Which of the following statements is NOT correct?
Question 703 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $500 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $500. Each player can flip a coin and if they flip heads, they receive $500. If they flip tails then they will lose $500. Which of the following statements is NOT correct?

Question 704 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $256 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $256. Each player can flip a coin and if they flip heads, they receive $256. If they flip tails then they will lose $256. Which of the following statements is NOT correct?

Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Which of the following statements is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
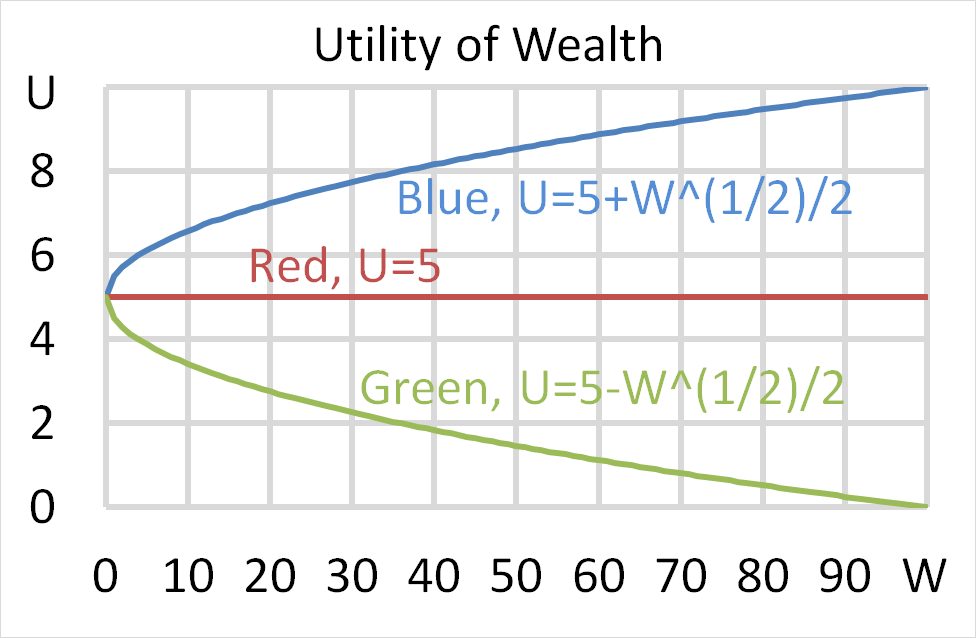
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Government bonds currently have a return of 5% pa. A stock has an expected return of 6% pa and the market return is 7% pa. What is the beta of the stock?
Government bonds currently have a return of 5%. A stock has a beta of 2 and the market return is 7%. What is the expected return of the stock?
Which statement(s) are correct?
(i) All stocks that plot on the Security Market Line (SML) are fairly priced.
(ii) All stocks that plot above the Security Market Line (SML) are overpriced.
(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.
Select the most correct response:
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
Question 244 CAPM, SML, NPV, risk
Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?
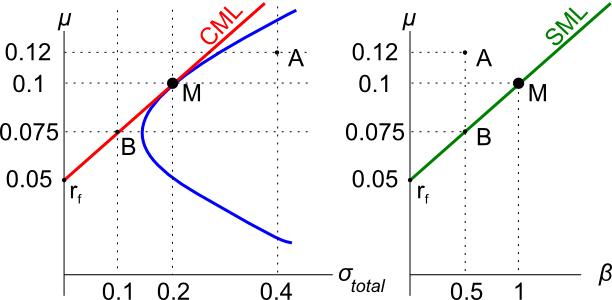
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
Stock A and B's returns have a correlation of 0.3. Which statement is NOT correct?
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A very low-risk stock just paid its semi-annual dividend of $0.14, as it has for the last 5 years. You conservatively estimate that from now on the dividend will fall at a rate of 1% every 6 months.
If the stock currently sells for $3 per share, what must be its required total return as an effective annual rate?
If risk free government bonds are trading at a yield of 4% pa, given as an effective annual rate, would you consider buying or selling the stock?
The stock's required total return is:
Diversification in a portfolio of two assets works best when the correlation between their returns is:
Find the sample standard deviation of returns using the data in the table:
| Stock Returns | |
| Year | Return pa |
| 2008 | 0.3 |
| 2009 | 0.02 |
| 2010 | -0.2 |
| 2011 | 0.4 |
The returns above and standard deviations below are given in decimal form.

Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
Fundamentalists who analyse company financial reports and news announcements (but who don't have inside information) will make positive abnormal returns if:
The efficient markets hypothesis (EMH) and no-arbitrage pricing theory are most closely related to which of the following concepts?
Question 100 market efficiency, technical analysis, joint hypothesis problem
A company selling charting and technical analysis software claims that independent academic studies have shown that its software makes significantly positive abnormal returns. Assuming the claim is true, which statement(s) are correct?
(I) Weak form market efficiency is broken.
(II) Semi-strong form market efficiency is broken.
(III) Strong form market efficiency is broken.
(IV) The asset pricing model used to measure the abnormal returns (such as the CAPM) had mis-specification error so the returns may not be abnormal but rather fair for the level of risk.
Select the most correct response:
Question 416 real estate, market efficiency, income and capital returns, DDM, CAPM
A residential real estate investor believes that house prices will grow at a rate of 5% pa and that rents will grow by 2% pa forever.
All rates are given as nominal effective annual returns. Assume that:
- His forecast is true.
- Real estate is and always will be fairly priced and the capital asset pricing model (CAPM) is true.
- Ignore all costs such as taxes, agent fees, maintenance and so on.
- All rental income cash flow is paid out to the owner, so there is no re-investment and therefore no additions or improvements made to the property.
- The non-monetary benefits of owning real estate and renting remain constant.
Which one of the following statements is NOT correct? Over time:
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
What do you think will be the stock's expected return over the next year, given as an effective annual rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
Over the last year, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. So ##r_{m} = (P_{0} - P_{-1})/P_{-1} = -0.01##, where the current time is zero and one year ago is time -1. The risk free rate was unchanged.
What do you think was the stock's historical return over the last year, given as an effective annual rate?
A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.
Ignoring the costs of financial distress, which of the following statements is NOT correct:
Question 408 leverage, portfolio beta, portfolio risk, real estate, CAPM
You just bought a house worth $1,000,000. You financed it with an $800,000 mortgage loan and a deposit of $200,000.
You estimate that:
- The house has a beta of 1;
- The mortgage loan has a beta of 0.2.
What is the beta of the equity (the $200,000 deposit) that you have in your house?
Also, if the risk free rate is 5% pa and the market portfolio's return is 10% pa, what is the expected return on equity in your house? Ignore taxes, assume that all cash flows (interest payments and rent) were paid and received at the end of the year, and all rates are effective annual rates.
A firm has a debt-to-equity ratio of 60%. What is its debt-to-assets ratio?
Question 572 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Which of the following statements about yield curves is NOT correct?
Question 573 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, liquidity premium theory, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Question 321 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 50 basis points due to high future GDP and inflation forecasts.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar will:
Question 699 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 701 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 702 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 513 stock split, reverse stock split, stock dividend, bonus issue, rights issue
Which of the following statements is NOT correct?
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 4 for 3 stock split. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order.
Question 566 capital structure, capital raising, rights issue, on market repurchase, dividend, stock split, bonus issue
A company's share price fell by 20% and its number of shares rose by 25%. Assume that there are no taxes, no signalling effects and no transaction costs.
Which one of the following corporate events may have happened?
Question 568 rights issue, capital raising, capital structure
A company conducts a 1 for 5 rights issue at a subscription price of $7 when the pre-announcement stock price was $10. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order. Ignore all taxes, transaction costs and signalling effects.
A company conducts a 2 for 3 rights issue at a subscription price of $8 when the pre-announcement stock price was $9. Assume that all investors use their rights to buy those extra shares.
What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
In mid 2009 the listed mining company Rio Tinto announced a 21-for-40 renounceable rights issue. Below is the chronology of events:
- 04/06/2009. Share price opens at $69.00 and closes at $66.90.
- 05/06/2009. 21-for-40 rights issue announced at a subscription price of $28.29.
- 16/06/2009. Last day that shares trade cum-rights. Share price opens at $76.40 and closes at $75.50.
- 17/06/2009. Shares trade ex-rights. Rights trading commences.
All things remaining equal, what would you expect Rio Tinto's stock price to open at on the first day that it trades ex-rights (17/6/2009)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
In late 2003 the listed bank ANZ announced a 2-for-11 rights issue to fund the takeover of New Zealand bank NBNZ. Below is the chronology of events:
- 23/10/2003. Share price closes at $18.30.
- 24/10/2003. 2-for-11 rights issue announced at a subscription price of $13. The proceeds of the rights issue will be used to acquire New Zealand bank NBNZ. Trading halt announced in morning before market opens.
- 28/10/2003. Trading halt lifted. Last (and only) day that shares trade cum-rights. Share price opens at $18.00 and closes at $18.14.
- 29/10/2003. Shares trade ex-rights.
All things remaining equal, what would you expect ANZ's stock price to open at on the first day that it trades ex-rights (29/10/2003)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
Question 668 buy and hold, market efficiency, idiom
A quote from the famous investor Warren Buffet: "Much success can be attributed to inactivity. Most investors cannot resist the temptation to constantly buy and sell."
Buffet is referring to the buy-and-hold strategy which is to buy and never sell shares. Which of the following is a disadvantage of a buy-and-hold strategy? Assume that share markets are semi-strong form efficient. Which of the following is NOT an advantage of the strict buy-and-hold strategy? A disadvantage of the buy-and-hold strategy is that it reduces:
Which of the following is NOT a valid method for estimating the beta of a company's stock? Assume that markets are efficient, a long history of past data is available, the stock possesses idiosyncratic and market risk. The variances and standard deviations below denote total risks.
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Covariance ##(\sigma_{A,B})## | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the standard deviation (not variance) of the above portfolio? Note that the stocks' covariance is given, not correlation.
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
All things remaining equal, the higher the correlation of returns between two stocks:
Question 556 portfolio risk, portfolio return, standard deviation
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 12% pa.
- Stock A has an expected return of 10% pa and a standard deviation of 20% pa.
- Stock B has an expected return of 15% pa and a standard deviation of 30% pa.
The correlation coefficient between stock A and B's expected returns is 70%.
What will be the annual standard deviation of the portfolio with this 12% pa target return?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the expected return of the above portfolio?
Question 558 portfolio weights, portfolio return, short selling
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 16% pa.
- Stock A has an expected return of 8% pa.
- Stock B has an expected return of 12% pa.
What portfolio weights should the investor have in stocks A and B respectively?
Which of the following quantities is commonly assumed to be normally distributed?
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.
Which of the below statements is NOT correct?
The symbol ##\text{GDR}_{0\rightarrow 1}## represents a stock's gross discrete return per annum over the first year. ##\text{GDR}_{0\rightarrow 1} = P_1/P_0##. The subscript indicates the time period that the return is mentioned over. So for example, ##\text{AAGDR}_{1 \rightarrow 3}## is the arithmetic average GDR measured over the two year period from years 1 to 3, but it is expressed as a per annum rate.
Which of the below statements about the arithmetic and geometric average GDR is NOT correct?
Question 721 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some Commonwealth Bank (CBA) shares. He has calculated CBA’s monthly returns for each month in the past 20 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 1% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.01=1\% \text{ per month}###He also found the standard deviation of these monthly returns which was 5% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.05=5\%\text{ per month}###Which of the below statements about Fred’s CBA shares is NOT correct? Assume that the past historical average return is the true population average of future expected returns.
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 720 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed.
In 5 years, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 778 CML, systematic and idiosyncratic risk, portfolio risk, CAPM
The capital market line (CML) is shown in the graph below. The total standard deviation is denoted by σ and the expected return is μ. Assume that markets are efficient so all assets are fairly priced.
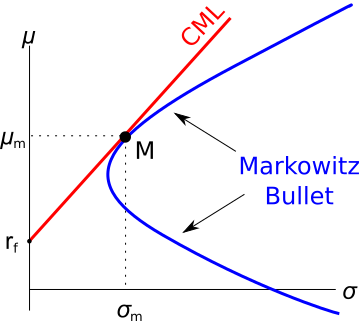
Which of the below statements is NOT correct?
A stock's total standard deviation of returns is 20% pa. The market portfolio's total standard deviation of returns is 15% pa. The beta of the stock is 0.8.
What is the stock's diversifiable standard deviation?
For a price of $129, Joanne will sell you a share which is expected to pay a $30 dividend in one year, and a $10 dividend every year after that forever. So the stock's dividends will be $30 at t=1, $10 at t=2, $10 at t=3, and $10 forever onwards.
The required return of the stock is 10% pa.
A three year bond has a face value of $100, a yield of 10% and a fixed coupon rate of 5%, paid semi-annually. What is its price?
Question 24 implicit interest rate in wholesale credit, effective rate
A bathroom and plumbing supplies shop offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given in this question are effective annual rates.
A wholesale horticulture nursery offers credit to its customers.
Customers are given 60 days to pay for their goods, but if they pay immediately they will get a 3% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay either immediately or on the 60th day. All rates given below are effective annual rates.
A wholesale glass importer offers credit to its customers. Customers are given 30 days to pay for their goods, but if they pay within 5 days they will get a 1% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 5th day or the 30th day. All rates given below are effective annual rates.
A wholesale building supplies business offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.
What is the effective interest rate implicit in the discount being offered?
Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given below are effective annual rates.
Question 65 annuity with growth, needs refinement
Which of the below formulas gives the present value of an annuity with growth?
Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###
The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.
The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.
###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###
The equation of a perpetuity with growth is:
###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.
For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.
The advantage of negative gearing is an example of the benefits of:
Question 469 franking credit, personal tax on dividends, imputation tax system, no explanation
A firm pays a fully franked cash dividend of $70 to one of its Australian shareholders who has a personal marginal tax rate of 45%. The corporate tax rate is 30%.
What will be the shareholder's personal tax payable due to the dividend payment?
The expression 'cash is king' emphasizes the importance of having enough cash to pay your short term debts to avoid bankruptcy. Which business decision is this expression most closely related to?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
Question 771 debt terminology, interest expense, interest tax shield, credit risk, no explanation
You deposit money into a bank account. Which of the following statements about this deposit is NOT correct?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?