Fight Finance

Question 574  inflation, real and nominal returns and cash flows, NPV

What is the present value of a nominal payment of $100 in 5 years? The real discount rate is 10% pa and the inflation rate is 3% pa.

(a) $71.2986

(b) $62.0921

(c) $61.5028

(d) $54.276

(e) $53.5612

Question 216  DDM

A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.

What is the implied growth rate of the dividend per year?

(a) -0.8565

(b) -0.0500

(c) -0.0435

(d) 0.0000

(e) 0.1500

Question 41  DDM, income and capital returns

The following is the Dividend Discount Model (DDM) used to price stocks:

### P_0 = \frac{d_1}{r-g} ###

Assume that the assumptions of the DDM hold and that the time period is measured in years.

Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?

(a) ## d_1(1+g)^3 ##

(b) ## P_3(r-g) ##

(c) ## d_2(1+g)^2 ##

(d) ## P_0(1+g)^3(r-g) ##

(e) ## P_0(1+g)^2(r-g) ##

Question 270  real estate, DDM, effective rate conversion

You own an apartment which you rent out as an investment property.

What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?

Assume that:

• You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
• The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
  So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
  Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)²), and then they will be constant for the next 12 months until the next year, and so on.
• The required return of the apartment is 8.732% pa, given as an effective annual rate.
• Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.

(a) $415,149.4048

(b) $438,252.6707

(c) $441,067.7356

(d) $444,155.5276

(e) $455,263.0844

Question 357  PE ratio, Multiples valuation

Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?

(a) Common equity in a listed public mining extraction company that will cease operations, wind up, and return all capital to shareholders in one year when its sole gold mine becomes depleted.

(b) Common equity in a small private owner-operated mining services company whose main asset is its sole tanker truck which delivers fuel to mines. The firm's shares are 100% owned by Bob, the driver of the tanker truck.

(c) Common equity in a large listed public company in the banking industry.

(d) Residential apartment real estate.

(e) Commercial warehouse real estate.

Question 457  PE ratio, Multiples valuation

Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.

(a) Highly liquid publically listed firms.

(b) Firms in a declining industry with very low or negative earnings growth.

(c) Firms expected to have temporarily low earnings over the next year, but with higher earnings later.

(d) Firms whose returns have a very low level of systematic risk.

(e) Firms whose assets include a very large proportion of cash.

Question 290  APR, effective rate, debt terminology

Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?

(a) An effective annual rate could be called: "a yearly rate compounding per year".

(b) An APR compounding monthly could be called: "a yearly rate compounding per month".

(c) An effective monthly rate could be called: "a yearly rate compounding per month".

(d) An APR compounding daily could be called: "a yearly rate compounding per day".

(e) An effective 2-year rate could be called: "a 2-year rate compounding every 2 years".

Question 49  inflation, real and nominal returns and cash flows, APR, effective rate

In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.

The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.

What is the real yield on these bonds, given as an APR compounding every 6 months?

(a) 0.3086%

(b) 0.6171%

(c) 0.6181%

(d) 0.6239%

(e) 0.6300%

Question 204  time calculation, fully amortising loan, APR

You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.

To your surprise, you can actually afford to pay $2,000 per month and your mortgage allows early repayments without fees. If you maintain these higher monthly payments, how long will it take to pay off your mortgage?

(a) 38.87 months, which is 3.24 yrs.

(b) 47.91 months, which is 3.99 yrs.

(c) 160.72 months, which is 13.39 yrs.

(d) 164.65 months, which is 13.72 yrs.

(e) None of the above.

Question 269  time calculation, APR

A student won $1m in a lottery. Currently the money is in a bank account which pays interest at 6% pa, given as an APR compounding per month.

She plans to spend $20,000 at the beginning of every month from now on (so the first withdrawal will be at t=0). After each withdrawal, she will check how much money is left in the account. When there is less than $500,000 left, she will donate that remaining amount to charity.

In how many months will she make her last withdrawal and donate the remainder to charity?

(a) In 31 months (t=31 months).

(b) In 30 months (t=30 months).

(c) In 28 months (t=28 months).

(d) In 27 months (t=27 months).

(e) In 26 months (t=26 months).

Question 195  equivalent annual cash flow

An industrial chicken farmer grows chickens for their meat. Chickens:

1. Cost $0.50 each to buy as chicks. They are bought on the day they’re born, at t=0.
2. Grow at a rate of $0.70 worth of meat per chicken per week for the first 6 weeks (t=0 to t=6).
3. Grow at a rate of $0.40 worth of meat per chicken per week for the next 4 weeks (t=6 to t=10) since they’re older and grow more slowly.
4. Feed costs are $0.30 per chicken per week for their whole life. Chicken feed is bought and fed to the chickens once per week at the beginning of the week. So the first amount of feed bought for a chicken at t=0 costs $0.30, and so on.
5. Can be slaughtered (killed for their meat) and sold at no cost at the end of the week. The price received for the chicken is their total value of meat (note that the chicken grows fast then slow, see above).

The required return of the chicken farm is 0.5% given as an effective weekly rate.

Ignore taxes and the fixed costs of the factory. Ignore the chicken’s welfare and other environmental and ethical concerns.

Find the equivalent weekly cash flow of slaughtering a chicken at 6 weeks and at 10 weeks so the farmer can figure out the best time to slaughter his chickens. The choices below are given in the same order, 6 and 10 weeks.

(a) $0.3651, $0.2374

(b) $0.3172, $0.3506

(c) $0.3065, $0.2157

(d) $0.3050, $0.2142

(e) $0.0157, $0.0491

Question 105  NPV, risk, market efficiency

A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.

What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).

(a) $10

(b) $3

(c) $2.8037

(d) $2.7273

(e) $0

Question 55  NPV, DDM

A stock is expected to pay the following dividends:

Cash Flows of a Stock
Time (yrs)	0	1	2	3	4	...
Dividend ($)	0.00	1.15	1.10	1.05	1.00	...

After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,

• the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
• the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.

The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.

What will be the price of the stock in four and a half years (t = 4.5)?

(a) $5.2615

(b) $6.0386

(c) $6.3333

(d) $6.6425

(e) $11.9040

Question 20  NPV, APR, Annuity

Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.

If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?

(a) -648.51

(b) 60.28

(c) 70.88

(d) 125.51

(e) 200

Question 22  NPV, perpetuity with growth, effective rate, effective rate conversion

What is the NPV of the following series of cash flows when the discount rate is 10% given as an effective annual rate?

The first payment of $90 is in 3 years, followed by payments every 6 months in perpetuity after that which shrink by 3% every 6 months. That is, the growth rate every 6 months is actually negative 3%, given as an effective 6 month rate. So the payment at ## t=3.5 ## years will be ## 90(1-0.03)^1=87.3 ##, and so on.

(a) $899.88

(b) $858.00

(c) 545.53

(d) $520.14

(e) $65.74

Question 63  bond pricing, NPV, market efficiency

The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.

Considering this, which of the following statements is NOT correct?

(a) The internal rate of return (IRR) of buying a bond is equal to the bond's yield.

(b) The present value of a fairly priced bond's coupons and face value is equal to its price.

(c) If the required return of a bond falls, its price will fall.

(d) Fairly priced discount bonds' yield is more than the coupon rate, price is less than face value, and the NPV of buying them is zero.

(e) The NPV of buying a fairly priced bond is zero.

Question 140  IRR, NPV, profitability index

A project has an internal rate of return (IRR) which is greater than its required return. Select the most correct statement.

(a) The NPV will be negative and the profitability index will be less than 1.

(b) The NPV will be positive and the profitability index will be more than 1.

(c) The payback period will be positive and the Accounting Rate of Return will be more than the target return.

(d) The NPV will be positive and the profitability index will be negative.

(e) The NPV will be negative and the profitability index will be positive.

Question 503  DDM, NPV, stock pricing

A share currently worth $100 is expected to pay a constant dividend of $4 for the next 5 years with the first dividend in one year (t=1) and the last in 5 years (t=5).

The total required return is 10% pa.

What do you expected the share price to be in 5 years, just after the dividend at that time has been paid?

(a) $100

(b) $115.16

(c) $136.63

(d) $161.05

(e) $185.47

Question 56  income and capital returns, bond pricing, premium par and discount bonds

Which of the following statements about risk free government bonds is NOT correct?

(a) Premium bonds have a positive expected capital return.

(b) Discount bonds have a positive expected capital return.

(c) Par bonds have a zero expected capital return.

(d) Par bonds have a total expected yield equal to their coupon yield.

(e) Zero coupon bonds selling at par would have zero expected total, income and capital yields.

Hint: Total return can be broken into income and capital returns as follows:

###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###

The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.

Question 263  DDM, income and capital returns

A company's shares just paid their annual dividend of $2 each.

The stock price is now $40 (just after the dividend payment). The annual dividend is expected to grow by 3% every year forever. The assumptions of the dividend discount model are valid for this company.

What do you expect the effective annual dividend yield to be in 3 years (dividend yield from t=3 to t=4)?

(a) 0.03

(b) 0.0409

(c) 0.044

(d) 0.05

(e) 0.0515

Question 218  NPV, IRR, profitability index, average accounting return

Which of the following statements is NOT correct?

(a) If a project has a positive NPV, its Profitability Index (PI) will be more than 1.

(b) If a project has a negative NPV and the discount rate is zero, then the payback period will be infinite so the project will never pay back its costs.

(c) If a project's NPV is zero, then the PI must be 1.

(d) If a project has a negative NPV, its IRR will be negative.

(e) If a project has a positive NPV, its Average Accounting Return (AAR) is not necessarily positive, it could be positive, negative or zero.

Question 52  IRR, pay back period

A three year project's NPV is negative. The cash flows of the project include a negative cash flow at the very start and positive cash flows over its short life. The required return of the project is 10% pa. Select the most correct statement.

(a) The payback period is negative.

(b) The project's IRR is negative.

(c) The project's IRR is less than its required return.

(d) The project's IRR is more than its required return.

(e) The project's IRR is equal to its required return.

Question 197  credit risk, bank accepted bill

A highly levered risky firm is trying to raise more debt. The types of debt being considered, in no particular order, are senior bonds, junior bonds, bank accepted bills, promissory notes and bank loans.

Which of these forms of debt is the safest from the perspective of the debt investors who are thinking of investing in the firm's new debt?

(a) Senior bonds

(b) Junior bonds

(c) Bank accepted bills

(d) Promissory notes

(e) Bank loans

Question 24  implicit interest rate in wholesale credit, effective rate

A bathroom and plumbing supplies shop offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.

What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given in this question are effective annual rates.

(a) 0.0004

(b) 0.1299

(c) 0.1308

(d) 0.1377

(e) 0.1493

Question 146  APR, effective rate

A three year corporate bond yields 12% pa with a coupon rate of 10% pa, paid semi-annually.

Find the effective six month yield, effective annual yield and the effective daily yield. Assume that each month has 30 days and that there are 360 days in a year.

All answers are given in the same order:

##r_\text{eff semi-annual}##, ##r_\text{eff yearly}##, ##r_\text{eff daily}##.

(a) 0.06, 0.1236, 0.000324.

(b) 0.058301, 0.12, 0.000315.

(c) 0.05, 0.1025, 0.000271.

(d) 0.05, 0.1, 0.000278.

(e) 0.048809, 0.1, 0.000265.

Question 582  APR, effective rate, effective rate conversion

A credit card company advertises an interest rate of 18% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.

(a) The APR compounding monthly is 18.0000% per annum.

(b) The effective monthly rate is 1.5000% per month.

(c) The effective annual rate is 19.5618% per annum.

(d) The effective quarterly rate is 4.5678% per quarter.

(e) The APR compounding quarterly is 13.7035% per annum.

Question 211  equivalent annual cash flow

You're advising your superstar client 40-cent who is weighing up buying a private jet or a luxury yacht. 40-cent is just as happy with either, but he wants to go with the more cost-effective option. These are the cash flows of the two options:

• The private jet can be bought for $6m now, which will cost $12,000 per month in fuel, piloting and airport costs, payable at the end of each month. The jet will last for 12 years.
• Or the luxury yacht can be bought for $4m now, which will cost $20,000 per month in fuel, crew and berthing costs, payable at the end of each month. The yacht will last for 20 years.

What's unusual about 40-cent is that he is so famous that he will actually be able to sell his jet or yacht for the same price as it was bought since the next generation of superstar musicians will buy it from him as a status symbol.

Bank interest rates are 10% pa, given as an effective annual rate. You can assume that 40-cent will live for another 60 years and that when the jet or yacht's life is at an end, he will buy a new one with the same details as above.

Would you advise 40-cent to buy the or the ?

Note that the effective monthly rate is ##r_\text{eff monthly}=(1+0.1)^{1/12}-1=0.00797414##

Question 35  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

A European company just issued two bonds, a

• 1 year zero coupon bond at a yield of 8% pa, and a
• 2 year zero coupon bond at a yield of 10% pa.

What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.

(a) 0.0185

(b) 0.0374

(c) 0.0604

(d) 0.1204

(e) 0.1250

Question 460  bond pricing, premium par and discount bonds

Below are some statements about loans and bonds. The first descriptive sentence is correct. But one of the second sentences about the loans' or bonds' prices is not correct. Which statement is NOT correct? Assume that interest rates are positive.

Note that coupons or interest payments are the periodic payments made throughout a bond or loan's life. The face or par value of a bond or loan is the amount paid at the end when the debt matures.

(a) A bullet loan has no interest payments but it does have a face value. Therefore it's a discount loan.

(b) A fully amortising loan has interest payments but does not have a face value. Therefore it's a premium loan.

(c) An interest only loan has interest payments and its price and face value are equal. Therefore it's a par loan.

(d) A zero coupon bond has no coupon payments but it does have a face value. Therefore it's a premium bond.

(e) A balloon loan has interest payments and its face value is more than its price. Therefore it's a discount loan.

Question 255  bond pricing

In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.

A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?

(a) 94.20452353

(b) 100

(c) 106

(d) 112

(e) The bond is priceless.

Question 229  bond pricing

An investor bought two fixed-coupon bonds issued by the same company, a zero-coupon bond and a 7% pa semi-annual coupon bond. Both bonds have a face value of $1,000, mature in 10 years, and had a yield at the time of purchase of 8% pa.

A few years later, yields fell to 6% pa. Which of the following statements is correct? Note that a capital gain is an increase in price.

(a) The zero-coupon bond and the 7% semi-annual coupon bond were both discount bonds but now they are both premium bonds.

(b) The zero-coupon bond and the 7% semi-annual coupon bond were both premium bonds but now they are both discount bonds.

(c) When yields fell, the investor made a capital loss on both bonds.

(d) When yields fell, the investor made a capital gain on both bonds.

(e) When yields fell, the investor made a capital gain on the zero coupon bond but a loss on the 7% semi-annual coupon bond.

Question 178  bond pricing, premium par and discount bonds

Which one of the following bonds is trading at a discount?

(a) a ten-year bond with a $4000 face value whose yield to maturity is 6.0% and coupon rate is 6.5% paid semi-annually.

(b) a 6-year bond with a principal of $40,000 and a price of $45,000.

(c) a 15-year bond with a $10,000 face value whose yield to maturity is 8.0% and coupon rate is 10.0% paid semi-annually.

(d) a two-year bond with a $50,000 face value whose yield to maturity is 5.2% and coupon rate is 5.2% paid semi-annually.

(e) None of the above bonds are discount bonds.

Question 545  income and capital returns, fully amortising loan, no explanation

Which of the following statements about the capital and income returns of a 25 year fully amortising loan asset is correct?

Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.

Over the 25 years from issuance to maturity, a fully amortising loan's expected annual effective:

(a) Income and capital returns both rise.

(b) Income and capital returns both fall.

(c) Income return rises and its capital return falls.

(d) Income return falls and its capital return rises.

(e) Income and capital returns are constant.

Question 546  income and capital returns, interest only loan, no explanation

Which of the following statements about the capital and income returns of an interest-only loan is correct?

Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.

An interest-only loan's expected:

(a) Income and capital returns both rise over time.

(b) Income and capital returns both fall over time.

(c) Income return rises and its capital return falls over time.

(d) Income return falls and its capital return rises over time.

(e) Income and capital returns are constant through time.

Question 163  bond pricing, premium par and discount bonds

Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100), maturity (3 years) and yield (10%) as each other.

Which of the following statements is true?

(a) Bonds X and Y are premium bonds.

(b) Bonds X and Y are discount bonds.

(c) Bond X is a discount bond but bond Y is a premium bond.

(d) Bond X is a premium bond but bond Y is a discount bond.

(e) Bonds X and Y are par bonds.

Question 491  capital budgeting, opportunity cost, sunk cost

A man is thinking about taking a day off from his casual painting job to relax.

He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.

But he's thinking about the hours that he could work today (in the future) which are:

(a) A sunk cost.

(b) An opportunity cost.

(c) A negative side effect.

(d) A capital expense.

(e) A depreciation expense.

Question 173  CFFA

Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Candys Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	200
COGS	50
Operating expense	10
Depreciation	20
Interest expense	10
Income before tax	110
Tax at 30%	33
Net income	77

Candys Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	220	180
PPE
Cost	300	340
Accumul. depr.	60	40
Carrying amount	240	300
Total assets	460	480
Liabilities
Current liabilities	175	190
Non-current liabilities	135	130
Owners' equity
Retained earnings	50	60
Contributed equity	100	100
Total L and OE	460	480

 

Note: all figures are given in millions of dollars ($m).

(a) 242

(b) 182

(c) 112

(d) 92

(e) 52

Question 350  CFFA

Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Sidebar Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	405
COGS	100
Depreciation	34
Rent expense	22
Interest expense	39
Taxable Income	210
Taxes at 30%	63
Net income	147

Sidebar Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Cash	0	0
Inventory	70	50
Trade debtors	11	16
Rent paid in advance	4	3
PPE	700	680
Total assets	785	749
Trade creditors	11	19
Bond liabilities	400	390
Contributed equity	220	220
Retained profits	154	120
Total L and OE	785	749

 

Note: All figures are given in millions of dollars ($m).

The cash flow from assets was:

(a) $138m

(b) $142m

(c) $143m

(d) $172m

(e) $176m

Question 361  CFFA

Over the next year, the management of an unlevered company plans to:

• Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
• Pay dividends of $1m.
• Complete a $1.3m share buy-back.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2m

(b) $1m

(c) $0.4m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 223  CFFA, interest tax shield

Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?

(a) An increase in net capital spending.

(b) A decrease in the cash flow to creditors.

(c) An increase in interest expense.

(d) An increase in net working capital.

(e) A decrease in dividends paid.

Question 366  opportunity cost, NPV, CFFA

Your friend is trying to find the net present value of an investment which:

• Costs $1 million initially (t=0); and
• Pays a single positive cash flow of $1.1 million in one year (t=1).

The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.

Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.

He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).

He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.

Your friend has listed a few different ways to find the NPV which are written down below.

Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##

Method 2: ##-1m + 1.1m - 1m \times 0.1 ##

Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##

Which of the above calculations give the correct NPV? Select the most correct answer.

(a) Method 1 only.

(b) Method 2 only.

(c) Method 3 only.

(d) Methods 1 and 2 only.

(e) Methods 1 and 3 only.

Question 493  PE ratio

A firm has 2m shares and a market capitalisation of equity of $30m. The firm just announced earnings of $5m and paid an annual dividend of $0.75 per share.

What is the firm's (backward looking) price/earnings (PE) ratio?

(a) 2.5

(b) 3

(c) 6

(d) 15

(e) 20

Question 511  capital budgeting, CFFA

Find the cash flow from assets (CFFA) of the following project.

One Year Mining Project Data
Project life	1 year
Initial investment in building mine and equipment	$9m
Depreciation of mine and equipment over the year	$8m
Kilograms of gold mined at end of year	1,000
Sale price per kilogram	$0.05m
Variable cost per kilogram	$0.03m
Before-tax cost of closing mine at end of year	$4m
Tax rate	30%

Note 1: Due to the project, the firm also anticipates finding some rare diamonds which will give before-tax revenues of $1m at the end of the year.

Note 2: The land that will be mined actually has thermal springs and a family of koalas that could be sold to an eco-tourist resort for an after-tax amount of $3m right now. However, if the mine goes ahead then this natural beauty will be destroyed.

Note 3: The mining equipment will have a book value of $1m at the end of the year for tax purposes. However, the equipment is expected to fetch $2.5m when it is sold.

Find the project's CFFA at time zero and one. Answers are given in millions of dollars ($m), with the first cash flow at time zero, and the second at time one.

(a) -9,   15.65

(b) -9,   14.3

(c) -12,   16.8

(d) -12,   16.35

(e) -12,   14.3

Question 205  depreciation tax shield, CFFA

There are a number of ways that assets can be depreciated. Generally the government's tax office stipulates a certain method.

But if it didn't, what would be the ideal way to depreciate an asset from the perspective of a businesses owner?

(a) 'Straight line' or 'prime cost' depreciation, which allocates equal depreciation expenses over each year of the asset's life.

(b) 'Diminishing value' or 'reducing balance' depreciation, which allocates more depreciation expense at the start of the asset's life and less towards the end.

(c) No depreciation at all, so the asset is always kept on the books as being the same value that it was bought for. The asset will cause no depreciation expense in any year.

(d) Allocating all of the depreciation expense to the final year of the asset's life.

(e) Allocating all of the depreciation expense to the first year of the asset's life. Accountants would call this 'expensing' the asset, rather than 'capitalising' it and depreciating it slowly.

Question 225  CFFA

A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.

(a) Buy less land, buildings and trucks than what was planned. Assume that this has no impact on revenue.

(b) Pay off more debt than was planned, to reduce the firm’s interest expense.

(c) Change the depreciation method used for tax purposes from diminishing value to straight line, so less depreciation occurs this year and more occurs in later years. Assume that the government’s tax department allow this.

(d) Buying more inventory than was planned, so there is an increase in net working capital. Assume that there is no increase in sales.

(e) Raising new equity through a rights issue. Assume that all of the money raised is spent on new capital assets such as land and trucks, but they will be fitted out and delivered in one year so no new cash will be earned from them.

Question 238  CFFA, leverage, interest tax shield

A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.

Ignoring the costs of financial distress, which of the following statements is NOT correct:

(a) The company is increasing its debt-to-assets and debt-to-equity ratios. These are types of 'leverage' or 'gearing' ratios.

(b) The company will pay less tax to the government due to the benefit of interest tax shields.

(c) The company's net income, also known as earnings or net profit after tax, will fall.

(d) The company's expected levered firm free cash flow (FFCF or CFFA) will be higher due to tax shields.

(e) The company's expected levered equity free cash flow (EFCF) will not change.

Question 351  CFFA

Over the next year, the management of an unlevered company plans to:

• Achieve firm free cash flow (FFCF or CFFA) of $1m.
• Pay dividends of $1.8m
• Complete a $1.3m share buy-back.
• Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2.1m

(b) $1.3m

(c) $0.8m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 68  WACC, CFFA, capital budgeting

A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?

Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.

(a) The manufacturing firm's before-tax WACC.

(b) The manufacturing firm's after-tax WACC.

(c) A services firm's before-tax WACC, assuming that the services firm has the same debt-to-assets ratio as the manufacturing firm.

(d) A services firm's after-tax WACC, assuming that the services firm has the same debt-to-assets ratio as the manufacturing firm.

(e) The services firm's levered cost of equity.

Question 113  WACC, CFFA, capital budgeting

The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.

Assume the following:

• Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
• Motorola had a 20% after-tax WACC before it merged with Google.
• Google and Motorola have the same level of gearing.
• Both companies operate in a classical tax system.

You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.

The mobile phone manufacturing project's:

(a) Unlevered CFFA should be discounted by Google's 10% WACC after tax.

(b) Unlevered CFFA should be discounted by Motorola's 20% WACC after tax.

(c) Levered CFFA should be discounted by Google's 10% WACC after tax.

(d) Levered CFFA should be discounted by Motorola's 20% WACC after tax.

(e) Unlevered CFFA by 15%, the average of Google and Motorola's WACC after tax.

Question 367  CFFA, interest tax shield

There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.

Which of the below FFCF formulas include the interest tax shield in the cash flow?

###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###

The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.

###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###

(a) 1, 3, 5, 7, 9.

(b) 2, 4, 6, 8, 10.

(c) 1, 4, 6, 8, 10.

(d) 2, 3, 5, 7, 9.

(e) 1, 3, 5, 8, 10.

Question 411  WACC, capital structure

A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.

Which of the following statements is NOT correct, all things remaining equal?

(a) The firm's WACC before tax will rise.

(b) The firm's WACC after tax will rise.

(c) The firm's required return on equity will be lower.

(d) The firm's net income will be higher.

(e) The firm's free cash flow will be lower.

Question 111  portfolio risk, correlation

All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:

(a) The correlation between the stocks' returns rise.

(b) The correlation between the stocks' returns decline.

(c) The portfolio standard deviation declines.

(d) Both stocks' individual variances decline.

(e) Both stocks' individual standard deviations decline.

Question 82  portfolio return

Portfolio Details
Stock	Expected return	Standard deviation	Correlation	Dollars invested
A	0.1	0.4	0.5	60
B	0.2	0.6		140

What is the expected return of the above portfolio?

(a) 0.15

(b) 0.17

(c) 0.1908

(d) 0.2412

(e) 0.34

Question 83  portfolio risk, standard deviation

Portfolio Details
Stock	Expected return	Standard deviation	Correlation ##(\rho_{A,B})##	Dollars invested
A	0.1	0.4	0.5	60
B	0.2	0.6		140

What is the standard deviation (not variance) of returns of the above portfolio?

(a) 0.4368

(b) 0.4911

(c) 0.6331

(d) 0.6564

(e) 0.7348

Question 282  expected and historical returns, income and capital returns

You're the boss of an investment bank's equities research team. Your five analysts are each trying to find the expected total return over the next year of shares in a mining company. The mining firm:

• Is regarded as a mature company since it's quite stable in size and was floated around 30 years ago. It is not a high-growth company;
• Share price is very sensitive to changes in the price of the market portfolio, economic growth, the exchange rate and commodities prices. Due to this, its standard deviation of total returns is much higher than that of the market index;
• Experienced tough times in the last 10 years due to unexpected falls in commodity prices.
• Shares are traded in an active liquid market.

Your team of analysts present their findings, and everyone has different views. While there's no definitive true answer, whose calculation of the expected total return is the most plausible? Assume that:

• The analysts' source data is correct and true, but their inferences might be wrong;
• All returns and yields are given as effective annual nominal rates.

(a) Alice says 5% pa since she calculated that this was the average total yield on government bonds over the last 10 years. She says that this is also the expected total yield implied by current prices on one year government bonds.

(b) Bob says 4% pa since he calculated that this was the average total return on the mining stock over the last 10 years.

(c) Cate says 3% pa since she calculated that this was the average growth rate of the share price over the last 10 years.

(d) Dave says 6% pa since he calculated that this was the average growth rate of the share market price index (not the accumulation index) over the last 10 years.

(e) Eve says 15% pa since she calculated that this was the discount rate implied by the dividend discount model using the current share price, forecast dividend in one year and a 3% growth rate in dividends thereafter, which is the expected long term inflation rate.

Question 293  covariance, correlation, portfolio risk

All things remaining equal, the higher the correlation of returns between two stocks:

(a) The more diversification is possible when those stocks are combined in a portfolio.

(b) The lower the variance of returns of an equally-weighted portfolio of those stocks.

(c) The lower the volatility of returns of an equal-weighted portfolio of those stocks.

(d) The higher the covariance between those stocks' returns.

(e) The more likely that when one stock has a positive return, the other has a negative return.

Question 558  portfolio weights, portfolio return, short selling

An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 16% pa.

• Stock A has an expected return of 8% pa.
• Stock B has an expected return of 12% pa.

What portfolio weights should the investor have in stocks A and B respectively?

(a) 200%, -100%

(b) 200%, 100%

(c) -100%, 200%

(d) 100%, 200%

(e) -100%, 100%

Question 556  portfolio risk, portfolio return, standard deviation

An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 12% pa.

• Stock A has an expected return of 10% pa and a standard deviation of 20% pa.
• Stock B has an expected return of 15% pa and a standard deviation of 30% pa.

The correlation coefficient between stock A and B's expected returns is 70%.

What will be the annual standard deviation of the portfolio with this 12% pa target return?

(a) 24.28168% pa

(b) 24% pa

(c) 22.126907% pa

(d) 19.697716% pa

(e) 16.970563% pa

Question 562  covariance

What is the covariance of a variable X with itself?

The cov(X, X) or ##\sigma_{X,X}## equals:

(a) var(X) or ##\sigma_X^2##

(b) sd(X) or ##\sigma_X##

(c) 1

(d) 0

(e) Mathematically undefined

Question 564  covariance

What is the covariance of a variable X with a constant C?

The cov(X, C) or ##\sigma_{X,C}## equals:

(a) var(X) or ##\sigma_X^2##

(b) sd(X) or ##\sigma_X##

(c) 1

(d) 0

(e) Mathematically undefined

Question 565  correlation

What is the correlation of a variable X with a constant C?

The corr(X, C) or ##\rho_{X,C}## equals:

(a) var(X) or ##\sigma_X^2##

(b) sd(X) or ##\sigma_X##

(c) 1

(d) 0

(e) Mathematically undefined

Question 561  covariance, correlation

The covariance and correlation of two stocks X and Y's annual returns are calculated over a number of years. The units of the returns are in percent per annum ##(\% pa)##.

What are the units of the covariance ##(\sigma_{X,Y})## and correlation ##(\rho_{X,Y})## of returns respectively?

(a) Percentage points per annum ##(\text{pp pa})## and percentage points per annum ##(\text{pp pa})##.

(b) Percentage points per annum ##(\text{pp pa})## and percentage points per annum all squared ##\left( (\text{pp pa})^2 \right)##.

(c) Percentage points per annum all squared ##\left( (\text{pp pa})^2 \right)## and percentage points per annum ##(\text{pp pa})##.

(d) Percentage points per annum all squared ##\left( (\text{pp pa})^2 \right)## and percentage points per annum all squared ##\left( (\text{pp pa})^2 \right)##.

(e) Percentage points per annum all squared ##\left( (\text{pp pa})^2 \right)## and a pure number with no units.

Hint: Visit Wikipedia to understand the difference between percentage points ##(\text{pp})## and percent ##(\%)##.

Question 306  risk, standard deviation

Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.

What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?

Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.

(a) ##\sigma_\text{yearly} = \sigma_\text{monthly}##

(b) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times 12##

(c) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times 144##

(d) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times \sqrt{12}##

(e) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times {12}^{1/3}##

Question 90  CAPM, risk

According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?

(a) Global economic recession.

(b) A major terrorist attack, grounding all commercial aircraft in the US and Europe.

(c) An increase in corporate tax rates.

(d) The outbreak of world war.

(e) A company's poor earnings announcement.

Question 114  WACC, capital structure, risk

A firm's WACC before tax would decrease due to:

(a) the firm's industry becoming more systematically risky, for example if it was a mining company and commodities prices varied more strongly and were more positively correlated with the market portfolio.

(b) the firm's industry becoming less systematically risky, for example if it was a child care centre and the government announced permanently higher subsidies for parents' child care expenses.

(c) the firm issuing more debt and using the proceeds to repurchase stock.

(d) the firm issuing more equity and using the proceeds to pay off debt holders.

(e) none of the above.

Question 79  CAPM, risk

Which statement is the most correct?

(a) The risk free rate has zero systematic risk and zero idiosyncratic risk.

(b) The market portfolio has zero idiosyncratic risk.

(c) The market portfolio has zero systematic risk.

(d) a and b are true.

(e) a and c are true.

Question 98  capital structure, CAPM

A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.

According to the Capital Asset Pricing Model (CAPM), which statement is correct?

(a) The beta of the firm's assets will increase.

(b) The beta of the firm's assets will decrease.

(c) The beta of the firm's equity will increase.

(d) The beta of the firm's equity will decrease.

(e) The beta of the firm's equity will be unchanged.

Question 116  capital structure, CAPM

A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.

According to the Capital Asset Pricing Model (CAPM), which statement is correct?

(a) The beta of the firm's assets will increase.

(b) The beta of the firm's assets will decrease.

(c) The beta of the firm's equity will increase.

(d) The beta of the firm's equity will decrease.

(e) The beta of the firm's equity will be unchanged.

Question 248  CAPM, DDM, income and capital returns

The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):

###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###

Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:

###r_\text{total}=r_\text{income}+r_\text{capital}###

So the total return of an asset is the income component plus the capital or price growth component.

Another way to break up total return is to use the Capital Asset Pricing Model:

###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###

###r_\text{total}=r_\text{time value}+r_\text{risk premium}###

So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.

Using the above theory and your general knowledge, which of the below equations, if any, are correct?

(I) ##r_\text{income}=r_\text{time value}##

(II) ##r_\text{income}=r_\text{risk premium}##

(III) ##r_\text{capital}=r_\text{time value}##

(IV) ##r_\text{capital}=r_\text{risk premium}##

(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##

Which of the equations are correct?

(a) I, IV and V only.

(b) II, III and V only.

(c) V only.

(d) All are true.

(e) None are true.

Question 410  CAPM, capital budgeting

The CAPM can be used to find a business's expected opportunity cost of capital:

###r_i=r_f+β_i (r_m-r_f)###

What should be used as the risk free rate ##r_f##?

(a) The current central bank policy rate (RBA overnight money market rate).

(b) The current 30 day federal government treasury bill rate.

(c) The average historical 30 day federal government treasury bill rate over the last 20 years.

(d) The current 30 year federal government treasury bond rate.

(e) The average historical 30 year federal government treasury bond rate over the last 20 years.

Question 339  bond pricing, inflation, market efficiency, income and capital returns

Economic statistics released this morning were a surprise: they show a strong chance of consumer price inflation (CPI) reaching 5% pa over the next 2 years.

This is much higher than the previous forecast of 3% pa.

A vanilla fixed-coupon 2-year risk-free government bond was issued at par this morning, just before the economic news was released.

What is the expected change in bond price after the economic news this morning, and in the next 2 years? Assume that:

• Inflation remains at 5% over the next 2 years.
• Investors demand a constant real bond yield.
• The bond price falls by the (after-tax) value of the coupon the night before the ex-coupon date, as in real life.

(a) Today the price would have increased significantly.
Over the next 2 years, the bond price is expected to increase, measured on each ex-coupon date.

(b) Today the price would have increased significantly.
Over the next 2 years, the bond price is expected to be unchanged, measured on each ex-coupon date.

(c) Today the price would have been unchanged.
Over the next 2 years, the bond price is expected to increase, measured on each ex-coupon date.

(d) Today the price would have decreased significantly.
Over the next 2 years, the bond price is expected to increase, measured on each ex-coupon date.

(e) Today the price would have decreased significantly.
Over the next 2 years, the bond price is expected to be unchanged, measured on each ex-coupon date.

Question 340  market efficiency, opportunity cost

A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.

This fee is charged regardless of whether the fund makes gains or losses on your money.

The fund offers to invest your money in shares which have an expected return of 10% pa before fees.

You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.

What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:

• The fund has no private information.
• Markets are weak and semi-strong form efficient.
• The fund's transaction costs are negligible.
• The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.

(a) $0

(b) -$20,000.00

(c) -$48,000.17

(d) -$51,999.83

(e) -$80,000.00

Question 416  real estate, market efficiency, income and capital returns, DDM, CAPM

A residential real estate investor believes that house prices will grow at a rate of 5% pa and that rents will grow by 2% pa forever.

All rates are given as nominal effective annual returns. Assume that:

• His forecast is true.
• Real estate is and always will be fairly priced and the capital asset pricing model (CAPM) is true.
• Ignore all costs such as taxes, agent fees, maintenance and so on.
• All rental income cash flow is paid out to the owner, so there is no re-investment and therefore no additions or improvements made to the property.
• The non-monetary benefits of owning real estate and renting remain constant.

Which one of the following statements is NOT correct? Over time:

(a) The rental yield will fall and approach zero.

(b) The total return will fall and approach the capital return (5% pa).

(c) One or all of the following must fall: the systematic risk of real estate, the risk free rate or the market risk premium.

(d) If the country's nominal wealth growth rate is 4% pa and the nominal real estate growth rate is 5% pa then real estate will approach 100% of the country's wealth over time.

(e) If the country's nominal gross domestic production (GDP) growth rate is 4% pa and the nominal real estate rent growth rate is 2% pa then real estate rent will approach 100% of the country's GDP over time.

Question 70  payout policy

Due to floods overseas, there is a cut in the supply of the mineral iron ore and its price increases dramatically. An Australian iron ore mining company therefore expects a large but temporary increase in its profit and cash flows. The mining company does not have any positive NPV projects to begin, so what should it do? Select the most correct answer.

(a) Pay out the excess cash by increasing the regular dividend, and cutting it later.

(b) Pay out a special dividend.

(c) Conduct an on or off-market share repurchase.

(d) Conduct a share dividend (also called a 'bonus issue').

(e) Either b or c.

Question 202  DDM, payout policy

Currently, a mining company has a share price of $6 and pays constant annual dividends of $0.50. The next dividend will be paid in 1 year. Suddenly and unexpectedly the mining company announces that due to higher than expected profits, all of these windfall profits will be paid as a special dividend of $0.30 in 1 year.

If investors believe that the windfall profits and dividend is a one-off event, what will be the new share price? If investors believe that the additional dividend is actually permanent and will continue to be paid, what will be the new share price? Assume that the required return on equity is unchanged. Choose from the following, where the first share price includes the one-off increase in earnings and dividends for the first year only ##(P_\text{0 one-off})## , and the second assumes that the increase is permanent ##(P_\text{0 permanent})##:

(a) ##P_\text{0 one-off} = 9.6000, \space \space P_\text{0 permanent} = 6.2766##

(b) ##P_\text{0 one-off} = 6.3000, \space \space P_\text{0 permanent} = 6.2769##

(c) ##P_\text{0 one-off} = 9.6000, \space \space P_\text{0 permanent} = 6.3000##

(d) ##P_\text{0 one-off} = 6.2769, \space \space P_\text{0 permanent} = 9.6000##

(e) ##P_\text{0 one-off} = 6.3000, \space \space P_\text{0 permanent} = 9.6000##

Note: When a firm makes excess profits they sometimes pay them out as special dividends. Special dividends are just like ordinary dividends but they are one-off and investors do not expect them to continue, unlike ordinary dividends which are expected to persist.

Question 567  stock split, capital structure

A company conducts a 4 for 3 stock split. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order.

(a) -33.33%, 50%

(b) -25%, 33.33%

(c) -25%, 25%

(d) -20%, 25%

(e) 33.33%, -25%

Question 455  income and capital returns, payout policy, DDM, market efficiency

A fairly priced unlevered firm plans to pay a dividend of $1 next year (t=1) which is expected to grow by 3% pa every year after that. The firm's required return on equity is 8% pa.

The firm is thinking about reducing its future dividend payments by 10% so that it can use the extra cash to invest in more projects which are expected to return 8% pa, and have the same risk as the existing projects. Therefore, next year's dividend will be $0.90. No new equity or debt will be issued to fund the new projects, they'll all be funded by the cut in dividends.

What will be the stock's new annual capital return (proportional increase in price per year) if the change in payout policy goes ahead?

Assume that payout policy is irrelevant to firm value (so there's no signalling effects) and that all rates are effective annual rates.

(a) 2.7% pa.

(b) 3.0% pa.

(c) 3.5% pa.

(d) 3.3% pa.

(e) 3.8% pa.

Question 311  foreign exchange rate

When someone says that they're "buying American dollars" (USD), what type of asset are they probably buying? They're probably buying:

(a) Short term debt denominated in USD, for example lending to a US bank as a USD deposit.

(b) Long term debt denominated in USD, for example lending to a US company by buying their USD bonds.

(c) Shares denominated in USD, for example buying shares in Coca-Cola which is listed on the NYSE.

(d) Real estate denominated in USD, for example buying an apartment in Chicago.

(e) Commodities with USD, for example buying gold, wheat, or coal.

Question 313  foreign exchange rate, American and European terms

If the AUD appreciates against the USD, the American terms quote of the AUD will or ?

Question 316  foreign exchange rate, American and European terms

If the AUD appreciates against the USD, the European terms quote of the AUD will or ?

Question 317  foreign exchange rate, American and European terms

If the USD appreciates against the AUD, the European terms quote of the AUD will or ?

Question 319  foreign exchange rate, monetary policy, American and European terms

Investors expect the Reserve Bank of Australia (RBA) to keep the policy rate steady at their next meeting.

Then unexpectedly, the RBA announce that they will increase the policy rate by 25 basis points due to fears that the economy is growing too fast and that inflation will be above their target rate of 2 to 3 per cent.

What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:

(a) Appreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will increase.

(b) Depreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will decrease.

(c) Appreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will decrease.

(d) Depreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will increase.

(e) Appreciate against the USD, so the 'American terms' quote of the AUD (USD per AUD) will decrease.

Question 320  foreign exchange rate, monetary policy, American and European terms

Investors expect the Reserve Bank of Australia (RBA) to decrease the overnight cash rate at their next meeting.

Then unexpectedly, the RBA announce that they will keep the policy rate unchanged.

What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:

(a) Appreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will increase.

(b) Depreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will decrease.

(c) Appreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will decrease.

(d) Depreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will increase.

(e) Be unaffected by the change in the policy rate, so the exchange rate will remain the same.

Question 246  foreign exchange rate, forward foreign exchange rate, cross currency interest rate parity

Suppose the Australian cash rate is expected to be 8.15% pa and the US federal funds rate is expected to be 3.00% pa over the next 2 years, both given as nominal effective annual rates. The current exchange rate is at parity, so 1 USD = 1 AUD.

What is the implied 2 year forward foreign exchange rate?

(a) 1 USD = 1.1025 AUD

(b) 1.1025 USD = 1 AUD

(c) 1 USD = 1.05 AUD

(d) 1 USD = 1.1 AUD

(e) 1.1 USD = 1 AUD

Question 632  foreign exchange rate, no explanation

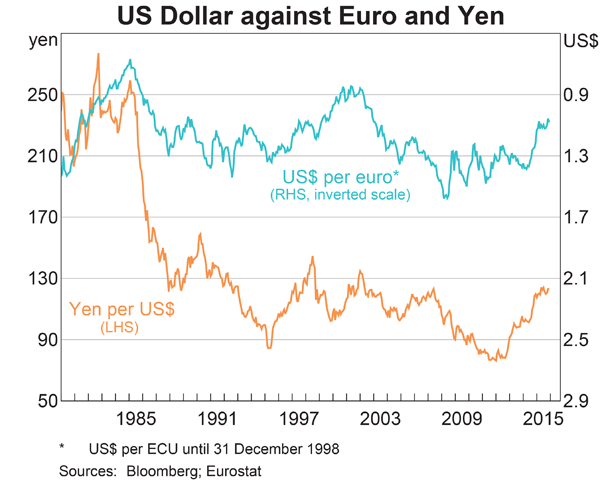
Below is a graph of the USD against the JPY and EUR from 1980 to 2015, compiled by the RBA. Select the correct statement about what occurred between 1980 and 2015. Note that in 1980 the euro was around 1.3 USD per EUR and the Yen was around 250 JPY per USD.

(a) The JPY and EUR both appreciated against the USD.

(b) The JPY and EUR both depreciated against the USD.

(c) The JPY appreciated against the USD while the EUR depreciated against the USD.

(d) The JPY depreciated against the USD while the EUR appreciated against the USD.

(e) The JPY and EUR both remained unchanged against the USD.

Question 555  capital budgeting, CFFA

Find the cash flow from assets (CFFA) of the following project.

Project Data
Project life	2 years
Initial investment in equipment	$8m
Depreciation of equipment per year for tax purposes	$3m
Unit sales per year	10m
Sale price per unit	$9
Variable cost per unit	$4
Fixed costs per year, paid at the end of each year	$2m
Tax rate	30%

Note 1: Due to the project, the firm will have to purchase $40m of inventory initially (at t=0). Half of this inventory will be sold at t=1 and the other half at t=2.

Note 2: The equipment will have a book value of $2m at the end of the project for tax purposes. However, the equipment is expected to fetch $1m when it is sold. Assume that the full capital loss is tax-deductible and taxed at the full corporate tax rate.

Note 3: The project will be fully funded by equity which investors will expect to pay dividends totaling $10m at the end of each year.

Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).

(a) -48,   54.5,   55.8

(b) -48,   54.5,   74.5

(c) -48,   74.5,   35.8

(d) -48,   74.5,   75.8

(e) -8,   74.5,   75.8

Question 74  WACC, capital structure, CAPM

A firm's weighted average cost of capital before tax (##r_\text{WACC before tax}##) would increase due to:

(a) The firm issuing more debt and using the proceeds to repurchase stock.

(b) The firm issuing more equity and using the proceeds to pay off debt holders.

(c) The firm's industry becoming more systematically risky, for example if it was a mining company whose performance became more sensitive to countries' GDP growth, so the correlation of the firm's returns with the market was higher.

(d) The firm's industry becoming less systematically risky, for example if it was a child care centre and the government announced higher subsidies for parents using child care centres, so the correlation of the firm's returns with the market was lower.

(e) None of the above.

Question 75  WACC, CAPM

A company has:

• 50 million shares outstanding.
• The market price of one share is currently $6.
• The risk-free rate is 5% and the market return is 10%.
• Market analysts believe that the company's ordinary shares have a beta of 2.
• The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
• The company's debentures are publicly traded and their market price is equal to 90% of their face value.
• The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.

What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.

(a) 11.75%

(b) 11.82%

(c) 13.54%

(d) 13.78%

(e) 20.84%

Question 104  CAPM, payout policy, capital structure, Miller and Modigliani, risk

Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.

For a firm operating in this perfect world, which statement(s) are correct?

(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.

(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.

(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.

Select the most correct response:

(a) Only (i) is true.

(b) Only (ii) is true.

(c) Only (iii) is true.

(d) Only (i) and (ii) are true.

(e) All statements (i), (ii) and (iii) are true.

Question 271  CAPM, option, risk, systematic risk, systematic and idiosyncratic risk

All things remaining equal, according to the capital asset pricing model, if the systematic variance of an asset increases, its required return will increase and its price will decrease.
If the idiosyncratic variance of an asset increases, its price will be unchanged.

What is the relationship between the price of a call or put option and the total, systematic and idiosyncratic variance of the underlying asset that the option is based on? Select the most correct answer.

Call and put option prices increase when the:

(a) Systematic variance of the underlying asset increases.

(b) Idiosyncratic variance of the underlying asset increases.

(c) Systematic, idiosyncratic or total variance of the underlying asset increases.

(d) Systematic variance of the underlying asset decreases.

(e) Systematic, idiosyncratic or total variance of the underlying asset decreases.

Question 628  CAPM, SML, risk

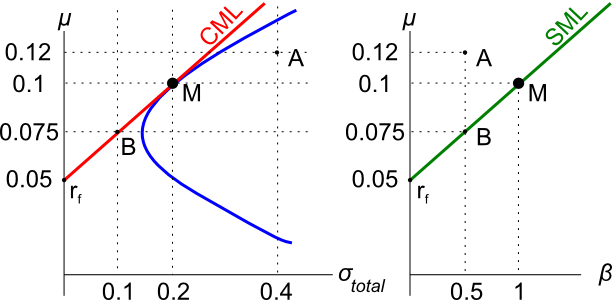
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?

(a) Asset A has the same systematic risk as asset B.

(b) Asset A has more total variance than asset B.

(c) Asset B has zero idiosyncratic risk. Asset B must be a portfolio of half the market portfolio and half government bonds.

(d) If risk-averse investors were forced to invest all of their wealth in a single risky asset, so they could not diversify, every investor would logically choose asset A over the other three assets.

(e) Assets M and B have the highest Sharpe ratios, which is defined as the gradient of the capital allocation line (CAL) from the government bonds through the asset on the graph of expected return versus total standard deviation.

Question 627  CAPM, SML, NPV, Jensens alpha

Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?

(a) Asset A has a Jensen's alpha of 4.5% pa.

(b) Asset A is under-priced.

(c) The NPV of buying asset A is zero.

(d) Asset B has a Jensen's alpha of zero.

(e) Asset B is fairly priced.

Question 617  systematic and idiosyncratic risk, risk, CAPM

A stock's required total return will increase when its:

(a) Systematic risk increases.

(b) Idiosyncratic risk increases.

(c) Total risk increases.

(d) Systematic risk decreases.

(e) Idiosyncratic risk decreases.

Question 450  CAPM, risk, portfolio risk, no explanation

The accounting identity states that the book value of a company's assets (A) equals its liabilities (L) plus owners equity (OE), so A = L + OE.

The finance version states that the market value of a company's assets (V) equals the market value of its debt (D) plus equity (E), so V = D + E.

Therefore a business's assets can be seen as a portfolio of the debt and equity that fund the assets.

Let ##\sigma_\text{V total}^2## be the total variance of returns on assets, ##\sigma_\text{V syst}^2## be the systematic variance of returns on assets, and ##\sigma_\text{V idio}^2## be the idiosyncratic variance of returns on assets, and ##\rho_\text{D idio, E idio}## be the correlation between the idiosyncratic returns on debt and equity.

Which of the following equations is NOT correct?

(a) ##r_V = \dfrac{D}{V}.r_D + \dfrac{E}{V}.r_E##

(b) ##\beta_V = \dfrac{D}{V}.\beta_D + \dfrac{E}{V}.\beta_E##

(c) ##\sigma_\text{V syst}^2 = \left(\dfrac{D}{V}\right)^2.\sigma_\text{D syst}^2 + \left(\dfrac{E}{V}\right)^2.\sigma_\text{E syst}^2##

(d) ##\sigma_\text{V idio}^2 = \left(\dfrac{D}{V}\right)^2.\sigma_\text{D idio}^2 + \left(\dfrac{E}{V}\right)^2.\sigma_\text{E idio}^2 + 2.\dfrac{D}{V}.\dfrac{E}{V}.\rho_\text{D idio, E idio}.\sigma_\text{D idio}.\sigma_\text{E idio}##

(e) ##\sigma_\text{V total}^2 = \left(\dfrac{D}{V}\right)^2.\sigma_\text{D total}^2 + \left(\dfrac{E}{V}\right)^2.\sigma_\text{E total}^2##

Question 343  CFFA, capital budgeting

An old company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.

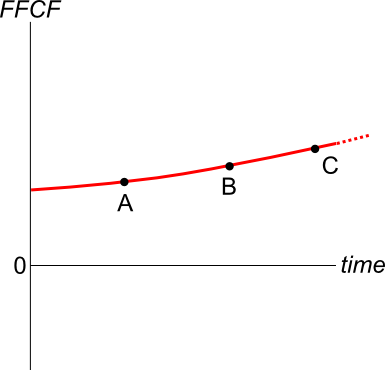
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:

###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###

Which point corresponds to the best time to calculate the terminal value?

(a) Point A.

(b) Point B.

(c) Point C.

(d) Any of the points.

(e) None of the points.

Question 344  CFFA, capital budgeting

A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.

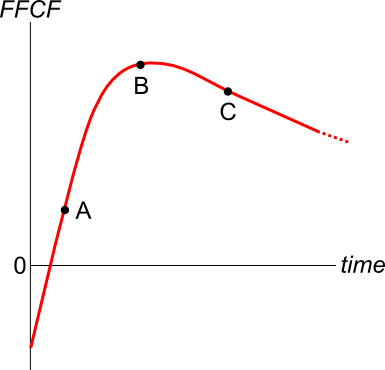
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:

###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###

Which point corresponds to the best time to calculate the terminal value?

(a) Point A.

(b) Point B.

(c) Point C.

(d) Any of the points.

(e) None of the points.

Question 237  WACC, Miller and Modigliani, interest tax shield

Which of the following discount rates should be the highest for a levered company? Ignore the costs of financial distress.

(a) Cost of debt (##r_\text{D}##).

(b) Unlevered cost of equity (##r_\text{E, U}##).

(c) Levered cost of equity (##r_\text{E, L}##).

(d) Levered before-tax WACC (##r_\text{V, LxITS}##).

(e) Levered after-tax WACC (##r_\text{V, LwITS}##).

Question 308  risk, standard deviation, variance, no explanation

A stock's standard deviation of returns is expected to be:

• 0.09 per month for the first 5 months;
• 0.14 per month for the next 7 months.

What is the expected standard deviation of the stock per year ##(\sigma_\text{annual})##?

Assume that returns are independently and identically distributed (iid) and therefore have zero auto-correlation.

(a) ##\sigma_\text{annual} = 0.09 \times 5 + 0.14 \times 7##

(b) ##\sigma_\text{annual} = (0.09 \times 5 + 0.14 \times 7)^{1/2}##

(c) ##\sigma_\text{annual} = (0.09^2 \times 5 + 0.14^2 \times 7)^{1/2}##

(d) ##\sigma_\text{annual} = (1+0.09)^5\times (1+0.14)^7 - 1##

(e) ##\sigma_\text{annual} = \left( \dfrac{0.09^2 \times 5 + 0.14^2 \times 7}{12} \right)^{1/2}##

Question 283  portfolio risk, correlation, needs refinement

Three important classes of investable risky assets are:

• Corporate debt which has low total risk,
• Real estate which has medium total risk,
• Equity which has high total risk.

Assume that the correlation between total returns on:

• Corporate debt and real estate is 0.1,
• Corporate debt and equity is 0.1,
• Real estate and equity is 0.5.

You are considering investing all of your wealth in one or more of these asset classes. Which portfolio will give the lowest total risk? You are restricted from shorting any of these assets. Disregard returns and the risk-return trade-off, pretend that you are only concerned with minimising risk.

(a) Most money in corporate debt, with some money in equity and real estate.

(b) Most money in equity, with some money in corporate debt and real estate.

(c) Most money in real estate, with some money in corporate debt and equity.

(d) Most money in corporate debt, with some money in real estate and none in equity.

(e) All money in corporate debt.

Question 65  annuity with growth, needs refinement

Which of the below formulas gives the present value of an annuity with growth?

(a) ##\dfrac{C_1}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

(b) ##\dfrac{C_1(1+g)^T}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

(c) ##\dfrac{C_1}{r-g}\left(1-\dfrac{1+g}{(1+r)^T}\right)##

(d) ##\dfrac{C_1}{r-g}\left(1-\left(\dfrac{1+g}{1+r}\right)^T \right)##

(e) ##\dfrac{C_1(1+g)}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###

The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.

The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.

###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###

The equation of a perpetuity with growth is:

###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###