Question 580 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to quadruple (be four times as big, say from $1 to $4) if the price grows by 15% pa?
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
For a price of $129, Joanne will sell you a share which is expected to pay a $30 dividend in one year, and a $10 dividend every year after that forever. So the stock's dividends will be $30 at t=1, $10 at t=2, $10 at t=3, and $10 forever onwards.
The required return of the stock is 10% pa.
For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.
The required return of the stock is 10% pa.
Suppose that the US government recently announced that subsidies for fresh milk producers will be gradually phased out over the next year. Newspapers say that there are expectations of a 40% increase in the spot price of fresh milk over the next year.
Option prices on fresh milk trading on the Chicago Mercantile Exchange (CME) reflect expectations of this 40% increase in spot prices over the next year. Similarly to the rest of the market, you believe that prices will rise by 40% over the next year.
What option trades are likely to be profitable, or to be more specific, result in a positive Net Present Value (NPV)?
Assume that:
- Only the spot price is expected to increase and there is no change in expected volatility or other variables that affect option prices.
- No taxes, transaction costs, information asymmetry, bid-ask spreads or other market frictions.
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
The below graph shows a project's net present value (NPV) against its annual discount rate.
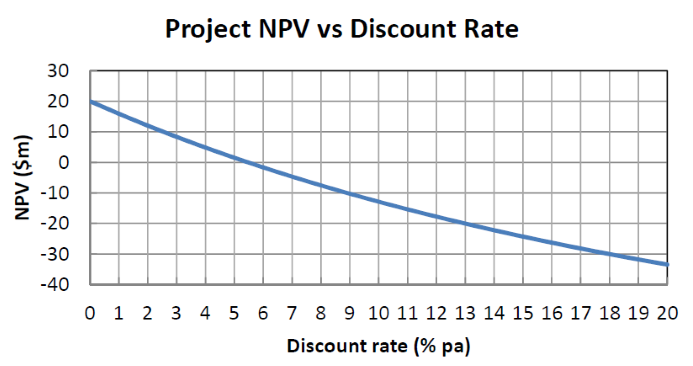
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
What is the net present value (NPV) of undertaking a full-time Australian undergraduate business degree as an Australian citizen? Only include the cash flows over the duration of the degree, ignore any benefits or costs of the degree after it's completed.
Assume the following:
- The degree takes 3 years to complete and all students pass all subjects.
- There are 2 semesters per year and 4 subjects per semester.
- University fees per subject per semester are $1,277, paid at the start of each semester. Fees are expected to remain constant in real terms for the next 3 years.
- There are 52 weeks per year.
- The first semester is just about to start (t=0). The first semester lasts for 19 weeks (t=0 to 19).
- The second semester starts immediately afterwards (t=19) and lasts for another 19 weeks (t=19 to 38).
- The summer holidays begin after the second semester ends and last for 14 weeks (t=38 to 52). Then the first semester begins the next year, and so on.
- Working full time at the grocery store instead of studying full-time pays $20/hr and you can work 35 hours per week. Wages are paid at the end of each week and are expected to remain constant in real terms.
- Full-time students can work full-time during the summer holiday at the grocery store for the same rate of $20/hr for 35 hours per week.
- The discount rate is 9.8% pa. All rates and cash flows are real. Inflation is expected to be 3% pa. All rates are effective annual.
The NPV of costs from undertaking the university degree is:
A student won $1m in a lottery. Currently the money is in a bank account which pays interest at 6% pa, given as an APR compounding per month.
She plans to spend $20,000 at the beginning of every month from now on (so the first withdrawal will be at t=0). After each withdrawal, she will check how much money is left in the account. When there is less than $500,000 left, she will donate that remaining amount to charity.
In how many months will she make her last withdrawal and donate the remainder to charity?
A newly floated farming company is financed with senior bonds, junior bonds, cumulative non-voting preferred stock and common stock. The new company has no retained profits and due to floods it was unable to record any revenues this year, leading to a loss. The firm is not bankrupt yet since it still has substantial contributed equity (same as paid-up capital).
On which securities must it pay interest or dividend payments in this terrible financial year?
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
One and a half years ago Frank bought a house for $600,000. Now it's worth only $500,000, based on recent similar sales in the area.
The expected total return on Frank's residential property is 7% pa.
He rents his house out for $1,600 per month, paid in advance. Every 12 months he plans to increase the rental payments.
The present value of 12 months of rental payments is $18,617.27.
The future value of 12 months of rental payments one year in the future is $19,920.48.
What is the expected annual rental yield of the property? Ignore the costs of renting such as maintenance, real estate agent fees and so on.
Question 461 book and market values, ROE, ROA, market efficiency
One year ago a pharmaceutical firm floated by selling its 1 million shares for $100 each. Its book and market values of equity were both $100m. Its debt totalled $50m. The required return on the firm's assets was 15%, equity 20% and debt 5% pa.
In the year since then, the firm:
- Earned net income of $29m.
- Paid dividends totaling $10m.
- Discovered a valuable new drug that will lead to a massive 1,000 times increase in the firm's net income in 10 years after the research is commercialised. News of the discovery was publicly announced. The firm's systematic risk remains unchanged.
Which of the following statements is NOT correct? All statements are about current figures, not figures one year ago.
Hint: Book return on assets (ROA) and book return on equity (ROE) are ratios that accountants like to use to measure a business's past performance.
###\text{ROA}= \dfrac{\text{Net income}}{\text{Book value of assets}}###
###\text{ROE}= \dfrac{\text{Net income}}{\text{Book value of equity}}###
The required return on assets ##r_V## is a return that financiers like to use to estimate a business's future required performance which compensates them for the firm's assets' risks. If the business were to achieve realised historical returns equal to its required returns, then investment into the business's assets would have been a zero-NPV decision, which is neither good nor bad but fair.
###r_\text{V, 0 to 1}= \dfrac{\text{Cash flow from assets}_\text{1}}{\text{Market value of assets}_\text{0}} = \dfrac{CFFA_\text{1}}{V_\text{0}}###
Similarly for equity and debt.
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0 | 6 | 12 | 18 | 20 | ... |
After year 4, the dividend will grow in perpetuity at 5% pa. The required return of the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in 7 years (t = 7), just after the dividend at that time has been paid?
The perpetuity with growth equation is:
###P_0=\dfrac{C_1}{r-g}###
Which of the following is NOT equal to the expected capital return as an effective annual rate?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in four and a half years (t = 4.5)?
The following is the Dividend Discount Model (DDM) used to price stocks:
###P_0=\dfrac{C_1}{r-g}###
If the assumptions of the DDM hold and the stock is fairly priced, which one of the following statements is NOT correct? The long term expected:
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.
What is the net present value (NPV) of borrowing from your friend?
Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.
What is the price of the share now?
Question 488 income and capital returns, payout policy, payout ratio, DDM
Two companies BigDiv and ZeroDiv are exactly the same except for their dividend payouts.
BigDiv pays large dividends and ZeroDiv doesn't pay any dividends.
Currently the two firms have the same earnings, assets, number of shares, share price, expected total return and risk.
Assume a perfect world with no taxes, no transaction costs, no asymmetric information and that all assets including business projects are fairly priced and therefore zero-NPV.
All things remaining equal, which of the following statements is NOT correct?
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
The boss of WorkingForTheManCorp has a wicked (and unethical) idea. He plans to pay his poor workers one week late so that he can get more interest on his cash in the bank.
Every week he is supposed to pay his 1,000 employees $1,000 each. So $1 million is paid to employees every week.
The boss was just about to pay his employees today, until he thought of this idea so he will actually pay them one week (7 days) later for the work they did last week and every week in the future, forever.
Bank interest rates are 10% pa, given as a real effective annual rate. So ##r_\text{eff annual, real} = 0.1## and the real effective weekly rate is therefore ##r_\text{eff weekly, real} = (1+0.1)^{1/52}-1 = 0.001834569##
All rates and cash flows are real, the inflation rate is 3% pa and there are 52 weeks per year. The boss will always pay wages one week late. The business will operate forever with constant real wages and the same number of employees.
What is the net present value (NPV) of the boss's decision to pay later?
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
You own a nice suit which you wear once per week on nights out. You bought it one year ago for $600. In your experience, suits used once per week last for 6 years. So you expect yours to last for another 5 years.
Your younger brother said that retro is back in style so he wants to wants to borrow your suit once a week when he goes out. With the increased use, your suit will only last for another 4 years rather than 5.
What is the present value of the cost of letting your brother use your current suit for the next 4 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new suit when your current one wears out and your brother will not use the new one; your brother will only use your current suit so he will only use it for the next four years; and the price of a new suit never changes.
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Currently, a mining company has a share price of $6 and pays constant annual dividends of $0.50. The next dividend will be paid in 1 year. Suddenly and unexpectedly the mining company announces that due to higher than expected profits, all of these windfall profits will be paid as a special dividend of $0.30 in 1 year.
If investors believe that the windfall profits and dividend is a one-off event, what will be the new share price? If investors believe that the additional dividend is actually permanent and will continue to be paid, what will be the new share price? Assume that the required return on equity is unchanged. Choose from the following, where the first share price includes the one-off increase in earnings and dividends for the first year only ##(P_\text{0 one-off})## , and the second assumes that the increase is permanent ##(P_\text{0 permanent})##:
Note: When a firm makes excess profits they sometimes pay them out as special dividends. Special dividends are just like ordinary dividends but they are one-off and investors do not expect them to continue, unlike ordinary dividends which are expected to persist.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
Question 239 income and capital returns, inflation, real and nominal returns and cash flows, interest only loan
A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.
From the bank's point of view, what is the long term expected nominal capital return of the loan asset?
Question 207 income and capital returns, bond pricing, coupon rate, no explanation
For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?
Let: ##P_0## be the bond price now,
##F_T## be the bond's face value,
##T## be the bond's maturity in years,
##r_\text{total}## be the bond's total yield,
##r_\text{income}## be the bond's income yield,
##r_\text{capital}## be the bond's capital yield, and
##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
An investor bought two fixed-coupon bonds issued by the same company, a zero-coupon bond and a 7% pa semi-annual coupon bond. Both bonds have a face value of $1,000, mature in 10 years, and had a yield at the time of purchase of 8% pa.
A few years later, yields fell to 6% pa. Which of the following statements is correct? Note that a capital gain is an increase in price.
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
Which one of the following bonds is trading at a discount?
Let the 'income return' of a bond be the coupon at the end of the period divided by the market price now at the start of the period ##(C_1/P_0)##. The expected income return of a premium fixed coupon bond is:
Question 535 DDM, real and nominal returns and cash flows, stock pricing
You are an equities analyst trying to value the equity of the Australian telecoms company Telstra, with ticker TLS. In Australia, listed companies like Telstra tend to pay dividends every 6 months. The payment around August is called the final dividend and the payment around February is called the interim dividend. Both occur annually.
- Today is mid-March 2015.
- TLS's last interim dividend of $0.15 was one month ago in mid-February 2015.
- TLS's last final dividend of $0.15 was seven months ago in mid-August 2014.
Judging by TLS's dividend history and prospects, you estimate that the nominal dividend growth rate will be 1% pa. Assume that TLS's total nominal cost of equity is 6% pa. The dividends are nominal cash flows and the inflation rate is 2.5% pa. All rates are quoted as nominal effective annual rates. Assume that each month is exactly one twelfth (1/12) of a year, so you can ignore the number of days in each month.
Calculate the current TLS share price.
A credit card company advertises an interest rate of 18% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
A firm has a debt-to-equity ratio of 25%. What is its debt-to-assets ratio?
A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
Question 213 income and capital returns, bond pricing, premium par and discount bonds
The coupon rate of a fixed annual-coupon bond is constant (always the same).
What can you say about the income return (##r_\text{income}##) of a fixed annual coupon bond? Remember that:
###r_\text{total} = r_\text{income} + r_\text{capital}###
###r_\text{total, 0 to 1} = \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0}###
Assume that there is no change in the bond's total annual yield to maturity from when it is issued to when it matures.
Select the most correct statement.
From its date of issue until maturity, the income return of a fixed annual coupon:
Radio-Rentals.com offers the Apple iphone 5S smart phone for rent at $12.95 per week paid in advance on a 2 year contract. After renting the phone, you must return it to Radio-Rentals.
Kogan.com offers the Apple iphone 5S smart phone for sale at $699. You estimate that the phone will last for 3 years before it will break and be worthless.
Currently, the effective annual interest rate is 11.351%, the effective monthly interest rate 0.9% and the effective weekly interest rate is 0.207%. Assume that there are exactly 52 weeks per year and 12 months per year.
Find the equivalent annual cost of renting the phone and also buying the phone. The answers below are listed in the same order.
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
A stock's required total return will increase when its:
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
Question 244 CAPM, SML, NPV, risk
Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:
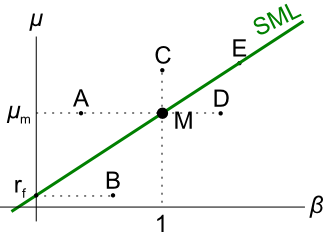
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
Which statement(s) are correct?
(i) All stocks that plot on the Security Market Line (SML) are fairly priced.
(ii) All stocks that plot above the Security Market Line (SML) are overpriced.
(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.
Select the most correct response:
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
Question 699 utility, risk aversion, utility function, gamble
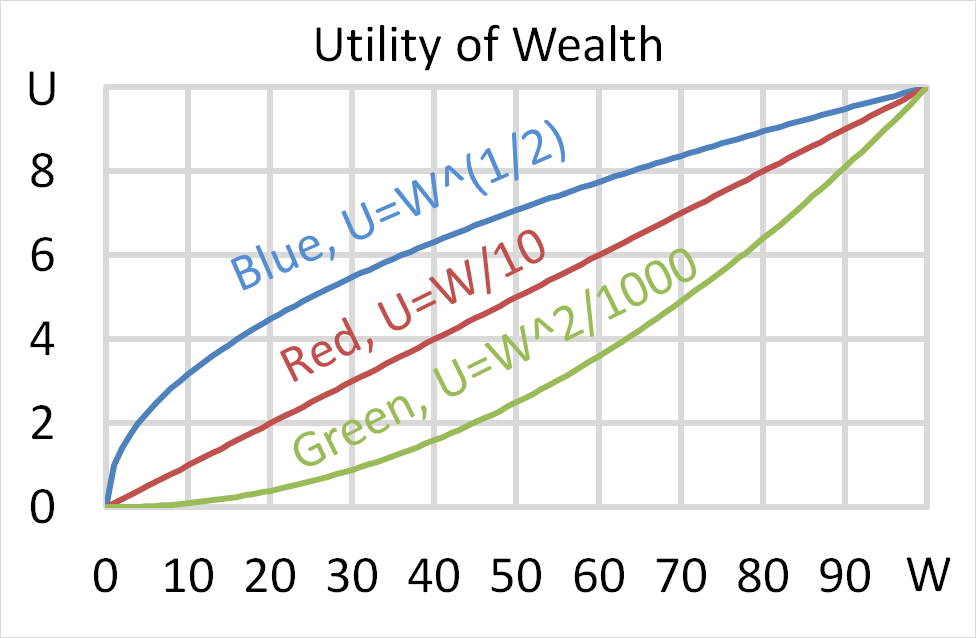
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?
"Buy low, sell high" is a well-known saying. It suggests that investors should buy low then sell high, in that order.
How would you re-phrase that saying to describe short selling?
Question 779 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some BHP shares. He has calculated BHP’s monthly returns for each month in the past 30 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 0.8% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.008=0.8\% \text{ per month}###He also found the standard deviation of these monthly returns which was 15% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.15=15\%\text{ per month}###Assume that the past historical average return is the true population average of future expected returns and the stock's returns calculated above ##(r_\text{t monthly})## are normally distributed. Which of the below statements about Fred’s BHP shares is NOT correct?
Stock A and B's returns have a correlation of 0.3. Which statement is NOT correct?