You bought a house, primarily funded using a home loan from a bank. Which of the following statements is NOT correct?
Question 771 debt terminology, interest expense, interest tax shield, credit risk, no explanation
You deposit money into a bank account. Which of the following statements about this deposit is NOT correct?
By convention, money market securities' yields are always quoted as:
Which of the following statements is NOT correct? Money market securities are:
A 180-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A bank bill was bought for $99,000 and sold for $100,000 thirty (30) days later. There are 365 days in the year. Which of the following formulas gives the simple interest rate per annum over those 30 days?
Note: To help you identify which is the correct answer without doing any calculations yourself, the formulas used to calculate the numbers are given.
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just agreed to a 30 year fully amortising mortgage loan with monthly payments of $2,500. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change. The below choices are given in the same order.
You want to buy a house priced at $400,000. You have saved a deposit of $40,000. The bank has agreed to lend you $360,000 as a fully amortising loan with a term of 30 years. The interest rate is 8% pa payable monthly and is not expected to change.
What will be your monthly payments?
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
The average weekly earnings of an Australian adult worker before tax was $1,542.40 per week in November 2014 according to the Australian Bureau of Statistics. Therefore average annual earnings before tax were $80,204.80 assuming 52 weeks per year. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below:
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $80,204.80 per annum before-tax?
In 2014 the median starting salaries of male and female Australian bachelor degree accounting graduates aged less than 25 years in their first full-time industry job was $50,000 before tax, according to Graduate Careers Australia. See page 9 of this report. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below.
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $50,000 per annum before-tax?
Question 448 franking credit, personal tax on dividends, imputation tax system
A small private company has a single shareholder. This year the firm earned a $100 profit before tax. All of the firm's after tax profits will be paid out as dividends to the owner.
The corporate tax rate is 30% and the sole shareholder's personal marginal tax rate is 45%.
The Australian imputation tax system applies because the company generates all of its income in Australia and pays corporate tax to the Australian Tax Office. Therefore all of the company's dividends are fully franked. The sole shareholder is an Australian for tax purposes and can therefore use the franking credits to offset his personal income tax liability.
What will be the personal tax payable by the shareholder and the corporate tax payable by the company?
Question 469 franking credit, personal tax on dividends, imputation tax system, no explanation
A firm pays a fully franked cash dividend of $70 to one of its Australian shareholders who has a personal marginal tax rate of 45%. The corporate tax rate is 30%.
What will be the shareholder's personal tax payable due to the dividend payment?
Question 494 franking credit, personal tax on dividends, imputation tax system
A firm pays a fully franked cash dividend of $100 to one of its Australian shareholders who has a personal marginal tax rate of 15%. The corporate tax rate is 30%.
What will be the shareholder's personal tax payable due to the dividend payment?
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid annually. So there's only one coupon per year, paid in arrears every year.
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid semi-annually. So there are two coupons per year, paid in arrears every six months.
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
Which one of the following bonds is trading at a discount?
A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?
A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 8 years and have a face value of $1,000 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue? All numbers are rounded up.
A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.
Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?
A young lady is trying to decide if she should attend university or not.
The young lady's parents say that she must attend university because otherwise all of her hard work studying and attending school during her childhood was a waste.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The hard work studying at school in her childhood should be classified as:
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
What is the Internal Rate of Return (IRR) of the project detailed in the table below?
Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.
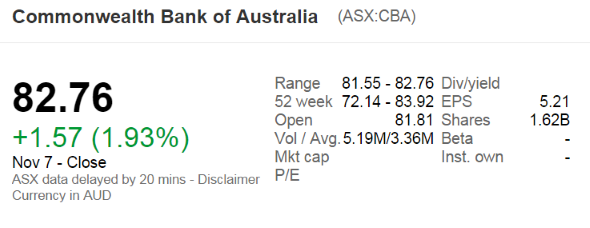
What was CBA's market capitalisation of equity?
Question 905 market capitalisation of equity, PE ratio, payout ratio
The below graph shows the computer software company Microsoft's stock price (MSFT) at the market close on the NASDAQ on Friday 1 June 2018.
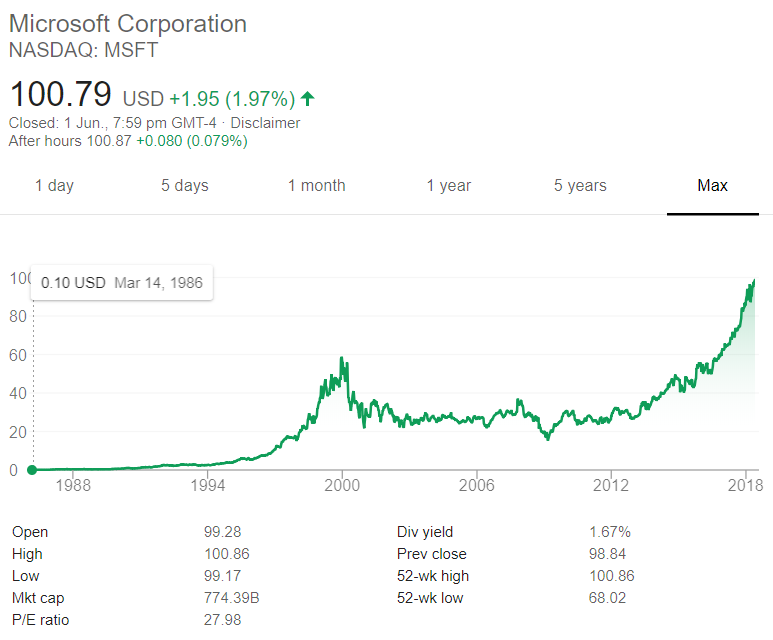
Based on the screenshot above, which of the following statements about MSFT is NOT correct? MSFT's:
The first payment of a constant perpetual annual cash flow is received at time 5. Let this cash flow be ##C_5## and the required return be ##r##.
So there will be equal annual cash flows at time 5, 6, 7 and so on forever, and all of the cash flows will be equal so ##C_5 = C_6 = C_7 = ...##
When the perpetuity formula is used to value this stream of cash flows, it will give a value (V) at time:
Question 25 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 2 year zero coupon bond at a yield of 8% pa, and a
- 3 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
In the home loan market, the acronym LVR stands for Loan to Valuation Ratio. If you bought a house worth one million dollars, partly funded by an $800,000 home loan, then your LVR was 80%. The LVR is equivalent to which of the following ratios?
One year ago you bought a $1,000,000 house partly funded using a mortgage loan. The loan size was $800,000 and the other $200,000 was your wealth or 'equity' in the house asset.
The interest rate on the home loan was 4% pa.
Over the year, the house produced a net rental yield of 2% pa and a capital gain of 2.5% pa.
Assuming that all cash flows (interest payments and net rental payments) were paid and received at the end of the year, and all rates are given as effective annual rates, what was the total return on your wealth over the past year?
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
A European company just issued two bonds, a
- 3 year zero coupon bond at a yield of 6% pa, and a
- 4 year zero coupon bond at a yield of 6.5% pa.
What is the company's forward rate over the fourth year (from t=3 to t=4)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 143 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 6-month zero coupon bond at a yield of 6% pa, and
- A 12 month zero coupon bond at a yield of 7% pa.
What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 572 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
A firm has a debt-to-equity ratio of 60%. What is its debt-to-assets ratio?
A firm has a debt-to-equity ratio of 25%. What is its debt-to-assets ratio?
A firm has a debt-to-assets ratio of 20%. What is its debt-to-equity ratio?
Question 573 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, liquidity premium theory, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Question 784 boot strapping zero coupon yield, forward interest rate, term structure of interest rates
Information about three risk free Government bonds is given in the table below.
| Federal Treasury Bond Data | ||||
| Maturity | Yield to maturity | Coupon rate | Face value | Price |
| (years) | (pa, compounding annually) | (pa, paid annually) | ($) | ($) |
| 1 | 0% | 2% | 100 | 102 |
| 2 | 1% | 2% | 100 | 101.9703951 |
| 3 | 2% | 2% | 100 | 100 |
Based on the above government bonds' yields to maturity, which of the below statements about the spot zero rates and forward zero rates is NOT correct?
A share was bought for $20 (at t=0) and paid its annual dividend of $3 one year later (at t=1). Just after the dividend was paid, the share price was $16 (at t=1). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
Which of the following statements about an asset’s standard deviation of returns is NOT correct? All other things remaining equal, the higher the asset’s standard deviation of returns:
The following table shows a sample of historical total returns of shares in two different companies A and B.
| Stock Returns | ||
| Total effective annual returns | ||
| Year | ##r_A## | ##r_B## |
| 2007 | 0.2 | 0.4 |
| 2008 | 0.04 | -0.2 |
| 2009 | -0.1 | -0.3 |
| 2010 | 0.18 | 0.5 |
What is the historical sample covariance (##\hat{\sigma}_{A,B}##) and correlation (##\rho_{A,B}##) of stock A and B's total effective annual returns?
Diversification in a portfolio of two assets works best when the correlation between their returns is:
Question 558 portfolio weights, portfolio return, short selling
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 16% pa.
- Stock A has an expected return of 8% pa.
- Stock B has an expected return of 12% pa.
What portfolio weights should the investor have in stocks A and B respectively?
The standard deviation and variance of a stock's annual returns are calculated over a number of years. The units of the returns are percent per annum ##(\% pa)##.
What are the units of the standard deviation ##(\sigma)## and variance ##(\sigma^2)## of returns respectively?
Hint: Visit Wikipedia to understand the difference between percentage points ##(\text{pp})## and percent ##(\%)##.
A stock has an expected return of 10% pa and you're 90% sure that over the next year, the return will be between -15% and 35%. The stock's returns are normally distributed. Note that the Z-statistic corresponding to a one-tail:
- 90% normal probability density function is 1.282.
- 95% normal probability density function is 1.645.
- 97.5% normal probability density function is 1.960.
What is the stock’s standard deviation of returns in percentage points per annum (pp pa)?
Question 559 variance, standard deviation, covariance, correlation
Which of the following statements about standard statistical mathematics notation is NOT correct?
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
What is the covariance of a variable X with a constant C?
The cov(X, C) or ##\sigma_{X,C}## equals:
Treasury bonds currently have a return of 5% pa. A stock has a beta of 0.5 and the market return is 10% pa. What is the expected return of the stock?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the price of the stock now?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
What do you think will be the stock's expected return over the next year, given as an effective annual rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
Over the last year, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. So ##r_{m} = (P_{0} - P_{-1})/P_{-1} = -0.01##, where the current time is zero and one year ago is time -1. The risk free rate was unchanged.
What do you think was the stock's historical return over the last year, given as an effective annual rate?
Question 807 market efficiency, expected and historical returns, CAPM, beta, systematic risk, no explanation
You work in Asia and just woke up. It looked like a nice day but then you read the news and found out that last night the American share market fell by 10% while you were asleep due to surprisingly poor macro-economic world news. You own a portfolio of liquid stocks listed in Asia with a beta of 1.6. When the Asian equity markets open, what do you expect to happen to your share portfolio? Assume that the capital asset pricing model (CAPM) is correct and that the market portfolio contains all shares in the world, of which American shares are a big part. Your portfolio beta is measured against this world market portfolio.
When the Asian equity market opens for trade, you would expect your portfolio value to:
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
Question 657 systematic and idiosyncratic risk, CAPM, no explanation
A stock's required total return will decrease when its:
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
Question 408 leverage, portfolio beta, portfolio risk, real estate, CAPM
You just bought a house worth $1,000,000. You financed it with an $800,000 mortgage loan and a deposit of $200,000.
You estimate that:
- The house has a beta of 1;
- The mortgage loan has a beta of 0.2.
What is the beta of the equity (the $200,000 deposit) that you have in your house?
Also, if the risk free rate is 5% pa and the market portfolio's return is 10% pa, what is the expected return on equity in your house? Ignore taxes, assume that all cash flows (interest payments and rent) were paid and received at the end of the year, and all rates are effective annual rates.
Question 809 Markowitz portfolio theory, CAPM, Jensens alpha, CML, systematic and idiosyncratic risk
A graph of assets’ expected returns ##(\mu)## versus standard deviations ##(\sigma)## is given in the graph below. The CML is the capital market line.
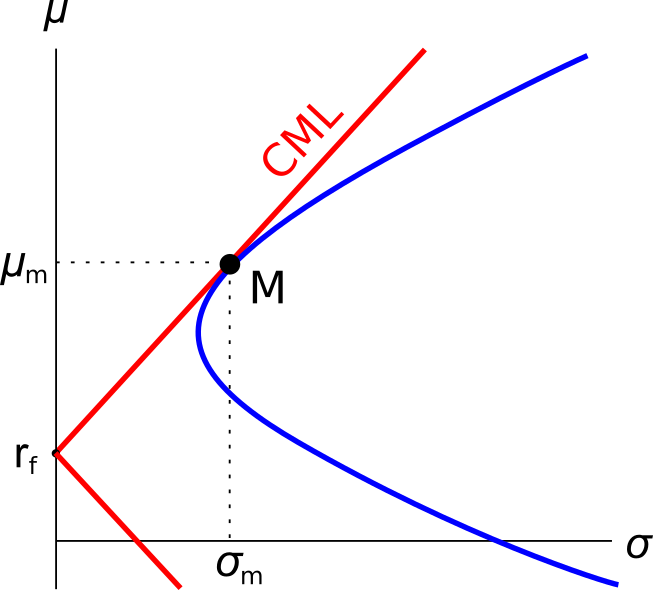
Which of the following statements about this graph, Markowitz portfolio theory and the Capital Asset Pricing Model (CAPM) theory is NOT correct?
Question 244 CAPM, SML, NPV, risk
Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:
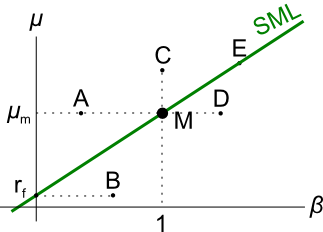
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
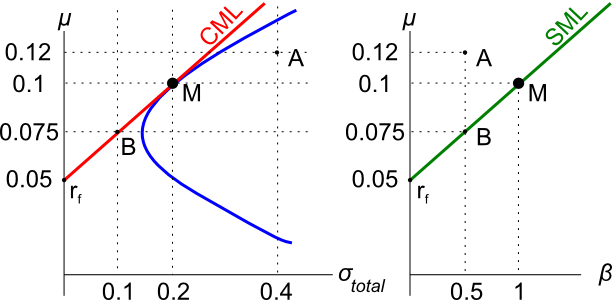
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?

Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?
You may assume:
- the value of debt (D) is constant through time,
- The cost of debt and the yield on debt are equal and given by ##r_D##.
- the appropriate rate to discount interest tax shields is ##r_D##.
- ##\text{IntExp}=D.r_D##
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.
For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.
The advantage of negative gearing is an example of the benefits of:
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
Question 772 interest tax shield, capital structure, leverage
A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?
On which date would the stock price increase if the dividend and earnings are higher than expected?
A company conducts a 4 for 3 stock split. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A firm conducts a two-for-one stock split. Which of the following consequences would NOT be expected?
Question 625 dividend re-investment plan, capital raising
Which of the following statements about dividend re-investment plans (DRP's) is NOT correct?
In the dividend discount model (DDM), share prices fall when dividends are paid. Let the high price before the fall be called the peak, and the low price after the fall be called the trough.
###P_0=\dfrac{C_1}{r-g}###
Which of the following statements about the DDM is NOT correct?
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Of the 15% pa total expected return, the dividend yield is expected to always be 7% pa and rest is the capital yield.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% total return lasts for the next 100 years (t=0 to 100), then reverts to 10% after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant, the dividends can only be re-invested at 10% pa and all returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
Question 446 working capital decision, corporate financial decision theory
The working capital decision primarily affects which part of a business?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
Which of the following decisions relates to the current assets and current liabilities of the firm?
Question 767 idiom, corporate financial decision theory, no explanation
The sayings "Don't cry over spilt milk", "Don't regret the things that you can't change" and "What's done is done" are most closely related to which financial concept?
Question 768 accounting terminology, book and market values, no explanation
Accountants and finance professionals have lots of names for the same things which can be quite confusing.
Which of the following groups of items are NOT synonyms?
Question 729 book and market values, balance sheet, no explanation
If a firm makes a profit and pays no dividends, which of the firm’s accounts will increase?
Question 737 financial statement, balance sheet, income statement
Where can a publicly listed firm's book value of equity be found? It can be sourced from the company's:
Question 738 financial statement, balance sheet, income statement
Where can a private firm's market value of equity be found? It can be sourced from the company's:
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
Question 524 risk, expected and historical returns, bankruptcy or insolvency, capital structure, corporate financial decision theory, limited liability
Which of the following statements is NOT correct?
Which of the following statements about book and market equity is NOT correct?
A 90 day bank bill has a face value of $100,000.
Investor A bought the bill when it was first issued at a simple yield to maturity of 3% pa and sold it 20 days later to Investor B who expected to earn a simple yield to maturity of 5% pa. Investor B held it until maturity.
Which of the following statements is NOT correct?
Jan asks you for a loan. He wants $100 now and offers to pay you back $120 in 1 year. You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate.
Ignore credit risk. Remember:
### V_0 = \frac{V_t}{(1+r_\text{eff})^t} ###
The current gold price is $700, gold storage costs are 2% pa and the risk free rate is 10% pa, both with continuous compounding.
What should be the 3 year gold futures price?
A 2-year futures contract on a stock paying a continuous dividend yield of 3% pa was bought when the underlying stock price was $10 and the risk free rate was 10% per annum with continuous compounding. Assume that investors are risk-neutral, so the stock's total required return is the risk free rate.
Find the forward price ##(F_2)## and value of the contract ##(V_0)## initially. Also find the value of the contract in 6 months ##(V_{0.5})## if the stock price rose to $12.
You want to buy an apartment worth $300,000. You have saved a deposit of $60,000.
The bank has agreed to lend you $240,000 as an interest only mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
Many Australian home loans that are interest-only actually require payments to be made on a fully amortising basis after a number of years.
You decide to borrow $600,000 from the bank at an interest rate of 4.25% pa for 25 years. The payments will be interest-only for the first 10 years (t=0 to 10 years), then they will have to be paid on a fully amortising basis for the last 15 years (t=10 to 25 years).
Assuming that interest rates will remain constant, what will be your monthly payments over the first 10 years from now, and then the next 15 years after that? The answer options are given in the same order.
A prospective home buyer can afford to pay $2,000 per month in mortgage loan repayments. The central bank recently lowered its policy rate by 0.25%, and residential home lenders cut their mortgage loan rates from 4.74% to 4.49%.
How much more can the prospective home buyer borrow now that interest rates are 4.49% rather than 4.74%? Give your answer as a proportional increase over the original amount he could borrow (##V_\text{before}##), so:
###\text{Proportional increase} = \frac{V_\text{after}-V_\text{before}}{V_\text{before}} ###Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates compounding per month.
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 4% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
Telsa Motors advertises that its Model S electric car saves $570 per month in fuel costs. Assume that Tesla cars last for 10 years, fuel and electricity costs remain the same, and savings are made at the end of each month with the first saving of $570 in one month from now.
The effective annual interest rate is 15.8%, and the effective monthly interest rate is 1.23%. What is the present value of the savings?
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 3 years from now (first payment at t=3).
- 1 payment of $600 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
There are many ways to write the ordinary annuity formula.
Which of the following is NOT equal to the ordinary annuity formula?
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 6.5 years from now (first payment at t=6.5).
- A single payment of $500 in 4 years and 3 months (t=4.25) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
You are promised 20 payments of $100, where the first payment is immediate (t=0) and the last is at the end of the 19th year (t=19). The effective annual discount rate is ##r##.
Which of the following equations does NOT give the correct present value of these 20 payments?
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.
For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $100, Andrea will sell you a 2 year bond paying annual coupons of 10% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.
An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
An investor bought a 20 year 5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly rose to 5.5% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
A stock is expected to pay its next dividend of $1 in one year. Future annual dividends are expected to grow by 2% pa. So the first dividend of $1 will be in one year, the year after that $1.02 (=1*(1+0.02)^1), and a year later $1.0404 (=1*(1+0.02)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
A stock just paid a dividend of $1. Future annual dividends are expected to grow by 2% pa. The next dividend of $1.02 (=1*(1+0.02)^1) will be in one year, and the year after that the dividend will be $1.0404 (=1*(1+0.02)^2), and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
For a price of $13, Carla will sell you a share paying a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.
The required return of the stock is 15% pa.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
The following is the Dividend Discount Model (DDM) used to price stocks:
###P_0=\dfrac{C_1}{r-g}###
If the assumptions of the DDM hold and the stock is fairly priced, which one of the following statements is NOT correct? The long term expected:
Question 748 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $2 tonight if you buy it today.
Thereafter the annual dividend is expected to grow by 3% pa, so the next dividend after the $2 one tonight will be $2.06 in one year, then in two years it will be $2.1218 and so on. The stock's required return is 8% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A fairly valued share's current price is $4 and it has a total required return of 30%. Dividends are paid annually and next year's dividend is expected to be $1. After that, dividends are expected to grow by 5% pa in perpetuity. All rates are effective annual returns.
What is the expected dividend income paid at the end of the second year (t=2) and what is the expected capital gain from just after the first dividend (t=1) to just after the second dividend (t=2)? The answers are given in the same order, the dividend and then the capital gain.
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
A stock is expected to pay its first dividend of $20 in 3 years (t=3), which it will continue to pay for the next nine years, so there will be ten $20 payments altogether with the last payment in year 12 (t=12).
From the thirteenth year onward, the dividend is expected to be 4% more than the previous year, forever. So the dividend in the thirteenth year (t=13) will be $20.80, then $21.632 in year 14, and so on forever. The required return of the stock is 10% pa. All rates are effective annual rates. Calculate the current (t=0) stock price.
A stock is expected to pay a dividend of $15 in one year (t=1), then $25 for 9 years after that (payments at t=2 ,3,...10), and on the 11th year (t=11) the dividend will be 2% less than at t=10, and will continue to shrink at the same rate every year after that forever. The required return of the stock is 10%. All rates are effective annual rates.
What is the price of the stock now?
Question 535 DDM, real and nominal returns and cash flows, stock pricing
You are an equities analyst trying to value the equity of the Australian telecoms company Telstra, with ticker TLS. In Australia, listed companies like Telstra tend to pay dividends every 6 months. The payment around August is called the final dividend and the payment around February is called the interim dividend. Both occur annually.
- Today is mid-March 2015.
- TLS's last interim dividend of $0.15 was one month ago in mid-February 2015.
- TLS's last final dividend of $0.15 was seven months ago in mid-August 2014.
Judging by TLS's dividend history and prospects, you estimate that the nominal dividend growth rate will be 1% pa. Assume that TLS's total nominal cost of equity is 6% pa. The dividends are nominal cash flows and the inflation rate is 2.5% pa. All rates are quoted as nominal effective annual rates. Assume that each month is exactly one twelfth (1/12) of a year, so you can ignore the number of days in each month.
Calculate the current TLS share price.
Question 488 income and capital returns, payout policy, payout ratio, DDM
Two companies BigDiv and ZeroDiv are exactly the same except for their dividend payouts.
BigDiv pays large dividends and ZeroDiv doesn't pay any dividends.
Currently the two firms have the same earnings, assets, number of shares, share price, expected total return and risk.
Assume a perfect world with no taxes, no transaction costs, no asymmetric information and that all assets including business projects are fairly priced and therefore zero-NPV.
All things remaining equal, which of the following statements is NOT correct?
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Itau Unibanco is a major listed bank in Brazil with a market capitalisation of equity equal to BRL 85.744 billion, EPS of BRL 3.96 and 2.97 billion shares on issue.
Banco Bradesco is another major bank with total earnings of BRL 8.77 billion and 2.52 billion shares on issue.
Estimate Banco Bradesco's current share price using a price-earnings multiples approach assuming that Itau Unibanco is a comparable firm.
Note that BRL is the Brazilian Real, their currency. Figures sourced from Google Finance on the market close of the BVMF on 24 July 2015.
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
A man is thinking about taking a day off from his casual painting job to relax.
He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.
But he's thinking about the hours that he could work today (in the future) which are:
A man has taken a day off from his casual painting job to relax.
It's the end of the day and he's thinking about the hours that he could have spent working (in the past) which are now:
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
What is the payback period of the project in years?
Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $500 at time 2 is actually earned smoothly from t=1 to t=2.
The below graph shows a project's net present value (NPV) against its annual discount rate.
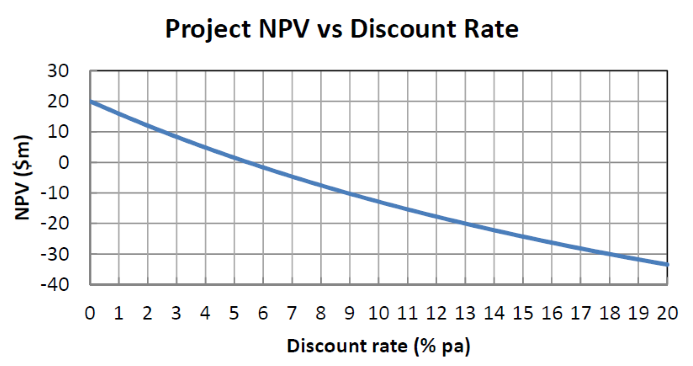
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
The below graph shows a project's net present value (NPV) against its annual discount rate.

Which of the following statements is NOT correct?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
You're considering a business project which costs $11m now and is expected to pay a single cash flow of $11m in one year. So you pay $11m now, then one year later you receive $11m.
Assume that the initial $11m cost is funded using the your firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about the net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
A firm is considering a business project which costs $10m now and is expected to pay a single cash flow of $12.1m in two years.
Assume that the initial $10m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
A pharmaceutical firm has just discovered a valuable new drug. So far the news has been kept a secret.
The net present value of making and commercialising the drug is $200 million, but $600 million of bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and bond raising to shareholders simultaneously in the same announcement. The bonds will be issued shortly after.
Once the announcement is made and the bonds are issued, what is the expected increase in the value of the firm's assets (ΔV), market capitalisation of debt (ΔD) and market cap of equity (ΔE)?
The triangle symbol is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##ΔV = ΔD+ΔE##
A mining firm has just discovered a new mine. So far the news has been kept a secret.
The net present value of digging the mine and selling the minerals is $250 million, but $500 million of new equity and $300 million of new bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and equity and bond raising to shareholders simultaneously in the same announcement. The shares and bonds will be issued shortly after.
Once the announcement is made and the new shares and bonds are issued, what is the expected increase in the value of the firm's assets ##(\Delta V)##, market capitalisation of debt ##(\Delta D)## and market cap of equity ##(\Delta E)##? Assume that markets are semi-strong form efficient.
The triangle symbol ##\Delta## is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##\Delta V = \Delta D+ \Delta E##
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
Question 556 portfolio risk, portfolio return, standard deviation
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 12% pa.
- Stock A has an expected return of 10% pa and a standard deviation of 20% pa.
- Stock B has an expected return of 15% pa and a standard deviation of 30% pa.
The correlation coefficient between stock A and B's expected returns is 70%.
What will be the annual standard deviation of the portfolio with this 12% pa target return?
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 6% pa.
- Stock A has an expected return of 5% pa.
- Stock B has an expected return of 10% pa.
What portfolio weights should the investor have in stocks A and B respectively?
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
Government bonds currently have a return of 5% pa. A stock has an expected return of 6% pa and the market return is 7% pa. What is the beta of the stock?
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_{0} = \frac{c_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What is the discount rate '## r_\text{eff} ##' in this equation?
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
An investor owns a portfolio with:
- 80% invested in stock A; and
- 20% invested in stock B.
Today there was a:
- 10% rise in stock A's price; and
- No change in stock B's price.
No dividends were paid on either stock. What was the total historical portfolio return on this day? All returns above and answer options below are given as effective daily rates.
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
All things remaining equal, the higher the correlation of returns between two stocks:
Suppose you had $100 in a savings account and the interest rate was 2% per year.
After 5 years, how much do you think you would have in the account if you left the money to grow?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
For a price of $6, Carlos will sell you a share which will pay a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $102, Andrea will sell you a share which just paid a dividend of $10 yesterday, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##10(1+0.05)^1=$10.50## in one year from now, and the year after it will be ##10(1+0.05)^2=11.025## and so on.
The required return of the stock is 15% pa.
For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.
The required return of the stock is 10% pa.
Question 65 annuity with growth, needs refinement
Which of the below formulas gives the present value of an annuity with growth?
Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###
The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.
The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.
###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###
The equation of a perpetuity with growth is:
###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###A company runs a number of slaughterhouses which supply hamburger meat to McDonalds. The company is afraid that live cattle prices will increase over the next year, even though there is widespread belief in the market that they will be stable. What can the company do to hedge against the risk of increasing live cattle prices? Which statement(s) are correct?
(i) buy call options on live cattle.
(ii) buy put options on live cattle.
(iii) sell call options on live cattle.
Select the most correct response:
The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
A stock has a beta of 0.5.
In the last 5 minutes, the federal government unexpectedly raised taxes. Over this time the share market fell by 3%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?