The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
Suppose that the US government recently announced that subsidies for fresh milk producers will be gradually phased out over the next year. Newspapers say that there are expectations of a 40% increase in the spot price of fresh milk over the next year.
Option prices on fresh milk trading on the Chicago Mercantile Exchange (CME) reflect expectations of this 40% increase in spot prices over the next year. Similarly to the rest of the market, you believe that prices will rise by 40% over the next year.
What option trades are likely to be profitable, or to be more specific, result in a positive Net Present Value (NPV)?
Assume that:
- Only the spot price is expected to increase and there is no change in expected volatility or other variables that affect option prices.
- No taxes, transaction costs, information asymmetry, bid-ask spreads or other market frictions.
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
Question 624 franking credit, personal tax on dividends, imputation tax system, no explanation
Which of the following statements about Australian franking credits is NOT correct? Franking credits:
Question 443 corporate financial decision theory, investment decision, financing decision, working capital decision, payout policy
Business people make lots of important decisions. Which of the following is the most important long term decision?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
You bought a house, primarily funded using a home loan from a bank. Which of the following statements is NOT correct?
High risk firms in danger of bankruptcy tend to have:
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
You work for XYZ company and you’ve been asked to evaluate a new project which has double the systematic risk of the company’s other projects.
You use the Capital Asset Pricing Model (CAPM) formula and input the treasury yield ##(r_f )##, market risk premium ##(r_m-r_f )## and the company’s asset beta risk factor ##(\beta_{XYZ} )## into the CAPM formula which outputs a return.
This return that you’ve just found is:
A share was bought for $20 (at t=0) and paid its annual dividend of $3 one year later (at t=1). Just after the dividend was paid, the share price was $16 (at t=1). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the expected return of the above portfolio?
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 3 years from now (first payment at t=3).
- 1 payment of $600 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
Your friend overheard that you need some cash and asks if you would like to borrow some money. She can lend you $5,000 now (t=0), and in return she wants you to pay her back $1,000 in two years (t=2) and every year after that for the next 5 years, so there will be 6 payments of $1,000 from t=2 to t=7 inclusive.
What is the net present value (NPV) of borrowing from your friend?
Assume that banks loan funds at interest rates of 10% pa, given as an effective annual rate.
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Question 780 mispriced asset, NPV, DDM, market efficiency, no explanation
A company advertises an investment costing $1,000 which they say is under priced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Of the 15% pa total expected return, the dividend yield is expected to be 4% pa and the capital yield 11% pa. Assume that the company's statements are correct.
What is the NPV of buying the investment if the 15% total return lasts for the next 100 years (t=0 to 100), then reverts to 10% after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant, the dividends can only be re-invested at 10% pa and all returns are given as effective annual rates. The answer choices below are given in the same order (15% for 100 years, and 15% forever):
An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
Question 748 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $2 tonight if you buy it today.
Thereafter the annual dividend is expected to grow by 3% pa, so the next dividend after the $2 one tonight will be $2.06 in one year, then in two years it will be $2.1218 and so on. The stock's required return is 8% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
A trader just bought a European style put option on CBA stock. The current option premium is $2, the exercise price is $75, the option matures in one year and the spot CBA stock price is $74.
Which of the following statements is NOT correct?
A stock is expected to pay a dividend of $5 per share in 1 month and $5 again in 7 months.
The stock price is $100, and the risk-free rate of interest is 10% per annum with continuous compounding. The yield curve is flat. Assume that investors are risk-neutral.
An investor has just taken a short position in a one year forward contract on the stock.
Find the forward price ##(F_1)## and value of the contract ##(V_0)## initially. Also find the value of the short futures contract in 6 months ##(V_\text{0.5, SF})## if the stock price fell to $90.
On 1 February 2016 you were told that your refinery company will need to purchase oil on 1 July 2016. You were afraid of the oil price rising between now and then so you bought some August 2016 futures contracts on 1 February 2016 to hedge against changes in the oil price. On 1 February 2016 the oil price was $40 and the August 2016 futures price was $43.
It's now 1 July 2016 and oil price is $45 and the August 2016 futures price is $46. You bought the spot oil and closed out your futures position on 1 July 2016.
What was the effective price paid for the oil, taking into account basis risk? All spot and futures oil prices quoted above and below are per barrel.
Question 797 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European put option will be exercised?
The price of gold is currently $700 per ounce. The forward price for delivery in 1 year is $800. An arbitrageur can borrow money at 10% per annum given as an effective discrete annual rate. Assume that gold is fairly priced and the cost of storing gold is zero.
What is the best way to conduct an arbitrage in this situation? The best arbitrage strategy requires zero capital, has zero risk and makes money straight away. An arbitrageur should sell 1 forward on gold and:
You intend to use futures on oil to hedge the risk of purchasing oil. There is no cross-hedging risk. Oil pays no dividends but it’s costly to store. Which of the following statements about basis risk in this scenario is NOT correct?
Question 834 option, delta, theta, gamma, standard deviation, Black-Scholes-Merton option pricing
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
| European Call Option | ||
| on a non-dividend paying stock | ||
| Description | Symbol | Quantity |
| Spot price ($) | ##S_0## | 20 |
| Strike price ($) | ##K_T## | 18 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.3 |
| Option maturity (years) | ##T## | 1 |
| Call option price ($) | ##c_0## | 3.939488 |
| Delta | ##\Delta = N[d_1]## | 0.747891 |
| ##N[d_2]## | ##N[d_2]## | 0.643514 |
| Gamma | ##\Gamma## | 0.053199 |
| Theta ($/year) | ##\Theta = \partial c / \partial T## | 1.566433 |
In general, stock prices tend to rise. What does this mean for futures on equity?
An equity index stands at 100 points and the one year equity futures price is 107.
The equity index is expected to have a dividend yield of 3% pa. Assume that investors are risk-neutral so their total required return on the shares is the same as the risk free Treasury bond yield which is 10% pa. Both are given as discrete effective annual rates.
Assuming that the equity index is fairly priced, an arbitrageur would recognise that the equity futures are:
A stock is expected to pay its semi-annual dividend of $1 per share for the foreseeable future. The current stock price is $40 and the continuously compounded risk free rate is 3% pa for all maturities. An investor has just taken a long position in a 12-month futures contract on the stock. The last dividend payment was exactly 4 months ago. Therefore the next $1 dividend is in 2 months, and the $1 dividend after is 8 months from now. Which of the following statements about this scenario is NOT correct?
You believe that the price of a share will fall significantly very soon, but the rest of the market does not. The market thinks that the share price will remain the same. Assuming that your prediction will soon be true, which of the following trades is a bad idea? In other words, which trade will NOT make money or prevent losses?
Question 271 CAPM, option, risk, systematic risk, systematic and idiosyncratic risk
All things remaining equal, according to the capital asset pricing model, if the systematic variance of an asset increases, its required return will increase and its price will decrease.
If the idiosyncratic variance of an asset increases, its price will be unchanged.
What is the relationship between the price of a call or put option and the total, systematic and idiosyncratic variance of the underlying asset that the option is based on? Select the most correct answer.
Call and put option prices increase when the:
A pig farmer in the US is worried about the price of hogs falling and wants to lock in a price now. In one year the pig farmer intends to sell 1,000,000 pounds of hogs. Luckily, one year CME lean hog futures expire on the exact day that he wishes to sell his pigs. The futures have a notional principal of 40,000 pounds (about 18 metric tons) and currently trade at a price of 63.85 cents per pound. The underlying lean hogs spot price is 77.15 cents per pound. The correlation between the futures price and the underlying hogs price is one and the standard deviations are both 4 cents per pound. The initial margin is USD1,500 and the maintenance margin is USD1,200 per futures contract.
Which of the below statements is NOT correct?
Question 904 option, Black-Scholes-Merton option pricing, option on future on stock index
A six month European-style call option on six month S&P500 index futures has a strike price of 2800 points.
The six month futures price on the S&P500 index is currently at 2740.805274 points. The futures underlie the call option.
The S&P500 stock index currently trades at 2700 points. The stock index underlies the futures. The stock index's standard deviation of continuously compounded returns is 25% pa.
The risk-free interest rate is 5% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
Question 921 utility, return distribution, log-normal distribution, arithmetic and geometric averages, no explanation
Who was the first theorist to propose the idea of ‘expected utility’?
Question 874 utility, return distribution, log-normal distribution, arithmetic and geometric averages
Who was the first theorist to endorse the maximisiation of the geometric average gross discrete return for investors (not gamblers) since it gave a "...portfolio that has a greater probability of being as valuable or more valuable than any other significantly different portfolio at the end of n years, n being large"?
Question 925 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, no explanation
The arithmetic average and standard deviation of returns on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 were calculated as follows:
###\bar{r}_\text{yearly} = \dfrac{ \displaystyle\sum\limits_{t=1992}^{24}{\left( \ln \left( \dfrac{P_{t+1}}{P_t} \right) \right)} }{T} = \text{AALGDR} =0.0949=9.49\% \text{ pa}###
###\sigma_\text{yearly} = \dfrac{ \displaystyle\sum\limits_{t=1992}^{24}{\left( \left( \ln \left( \dfrac{P_{t+1}}{P_t} \right) - \bar{r}_\text{yearly} \right)^2 \right)} }{T} = \text{SDLGDR} = 0.1692=16.92\text{ pp pa}###
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
Which of the following statements is NOT correct? If you invested $1m today in the ASX200, then over the next 4 years:
Question 927 mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the mean dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Question 785 fixed for floating interest rate swap, non-intermediated swap
The below table summarises the borrowing costs confronting two companies A and B.
| Bond Market Yields | ||||
| Fixed Yield to Maturity (%pa) | Floating Yield (%pa) | |||
| Firm A | 3 | L - 0.4 | ||
| Firm B | 5 | L + 1 | ||
Firm A wishes to borrow at a floating rate and Firm B wishes to borrow at a fixed rate. Design a non-intermediated swap that benefits firm A only. What will be the swap rate?
When does a European option's last-traded market price become a sunk cost?
Question 833 option, delta, theta, standard deviation, no explanation
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
A company has a 95% daily Value at Risk (VaR) of $1 million. The units of this VaR are in:
Question 791 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, log-normal distribution, VaR, confidence interval
A risk manager has identified that their pension fund’s continuously compounded portfolio returns are normally distributed with a mean of 5% pa and a standard deviation of 20% pa. The fund’s portfolio is currently valued at $1 million. Assume that there is no estimation error in the above figures. To simplify your calculations, all answers below use 2.33 as an approximation for the normal inverse cumulative density function at 99%. All answers are rounded to the nearest dollar. Which of the following statements is NOT correct?
Below is a table of the 'Risk-weights for residential mortgages' as shown in APRA Basel 3 Prudential Standard APS 112 Capital Adequacy: Standardised Approach to Credit Risk January 2013.
| LVR (%) |
Standard eligible mortgages |
Non-standard eligible mortgages |
||
|
|
Risk-weight (no mortgage insurance) % |
Risk-weight (with at least 40% of the mortgage insured by an acceptable LMI) % |
Risk-weight (no mortgage insurance) % |
Risk-weight (with at least 40% of the mortgage insured by an acceptable LMI) % |
| 0 – 60 |
35 |
35 |
50 |
35 |
| 60.01 – 80 |
35 |
35 |
75 |
50 |
| 80.01 – 90 |
50 |
35 |
100 |
75 |
| 90.01 – 100 |
75 |
50 |
100 |
75 |
| > 100.01 |
100 |
75 |
100 |
100 |
A bank is considering granting a home loan to a man to buy a house worth $1.25 million using his own funds and the loan. The loan would be standard with no lenders mortgage insurance (LMI) and an LVR of 80%.
What is the minimum regulatory capital that the bank requires to grant the home loan under the Basel 3 Accord? Ignore the capital conservation buffer.
The below graph from the RBA shows the phase-in of the Basel 3 minimum regulatory capital requirements under the Basel Committee on Banking Supervision (BCBS) on the left panel and in Australia under the Australian Prudential Regulatory Authority (APRA) on the right panel.
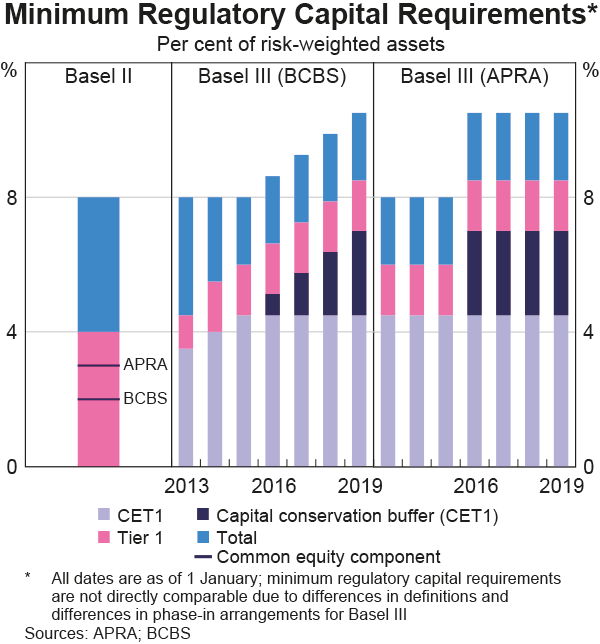
Which of the following statements about the Basel 3 minimum regulatory capital requirements as at 2019 is NOT correct? All minimum amounts exclude the 2.5% counter-cyclical buffer.
The Basel 3 minimum regulatory capital requirement as a percent of Risk Weighted Assets (RWA) is: