Fight Finance

Question 65  annuity with growth, needs refinement

Which of the below formulas gives the present value of an annuity with growth?

(a) ##\dfrac{C_1}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

(b) ##\dfrac{C_1(1+g)^T}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

(c) ##\dfrac{C_1}{r-g}\left(1-\dfrac{1+g}{(1+r)^T}\right)##

(d) ##\dfrac{C_1}{r-g}\left(1-\left(\dfrac{1+g}{1+r}\right)^T \right)##

(e) ##\dfrac{C_1(1+g)}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###

The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.

The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.

###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###

The equation of a perpetuity with growth is:

###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###

Question 141  time calculation, APR, effective rate

You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.

How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.

(a) 23.62

(b) 25.00

(c) 26.60

(d) 26.77

(e) 55.24

Question 193  bond pricing, premium par and discount bonds

Which one of the following bonds is trading at par?

(a) a ten-year bond with a $4000 face value whose yield to maturity is 6.0% and coupon rate is 6.5% paid semi-annually.

(b) a 6-year bond with a principal of $40,000 and a price of $45,000.

(c) a 15-year bond with a $10,000 face value whose yield to maturity is 8.0% and coupon rate is 10.0% paid semi-annually.

(d) a two-year bond with a $50,000 face value whose yield to maturity is 5.2% compounding semi-annually which has a price of $50,000.

(e) None of the above bonds are trading at par.

Question 207  income and capital returns, bond pricing, coupon rate, no explanation

For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?

Let: ##P_0## be the bond price now,

##F_T## be the bond's face value,

##T## be the bond's maturity in years,

##r_\text{total}## be the bond's total yield,

##r_\text{income}## be the bond's income yield,

##r_\text{capital}## be the bond's capital yield, and

##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.

(a) coupon rate = ##\dfrac{C_{0.5}+C_{1}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{total})^{0.5}+C_{1}}{P_0}##

(b) coupon rate = ##\dfrac{2 \times C_{0.5}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{capital})^{0.5}+C_{1}}{P_0}##

(c) coupon rate = ##\dfrac{2 \times C_{1}}{P_0}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}+C_{1}}{P_0}##

(d) coupon rate = ##\dfrac{2 \times C_{1}}{P_0}##, ##r_\text{income, 0 to 1}=\dfrac{2 \times C_{1}}{P_0}##

(e) coupon rate = ##\dfrac{2 \times C_{1}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{total})^{0.5}+C_{1}}{F_T}##

Question 276  derivative terminology, option

The 'option strike price' in an option contract, also known as the exercise price, is paid at the start when the option contract is agreed to. or ?

Question 319  foreign exchange rate, monetary policy, American and European terms

Investors expect the Reserve Bank of Australia (RBA) to keep the policy rate steady at their next meeting.

Then unexpectedly, the RBA announce that they will increase the policy rate by 25 basis points due to fears that the economy is growing too fast and that inflation will be above their target rate of 2 to 3 per cent.

What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:

(a) Appreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will increase.

(b) Depreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will decrease.

(c) Appreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will decrease.

(d) Depreciate against the USD, so the 'European terms' quote of the AUD (AUD per USD) will increase.

(e) Appreciate against the USD, so the 'American terms' quote of the AUD (USD per AUD) will decrease.

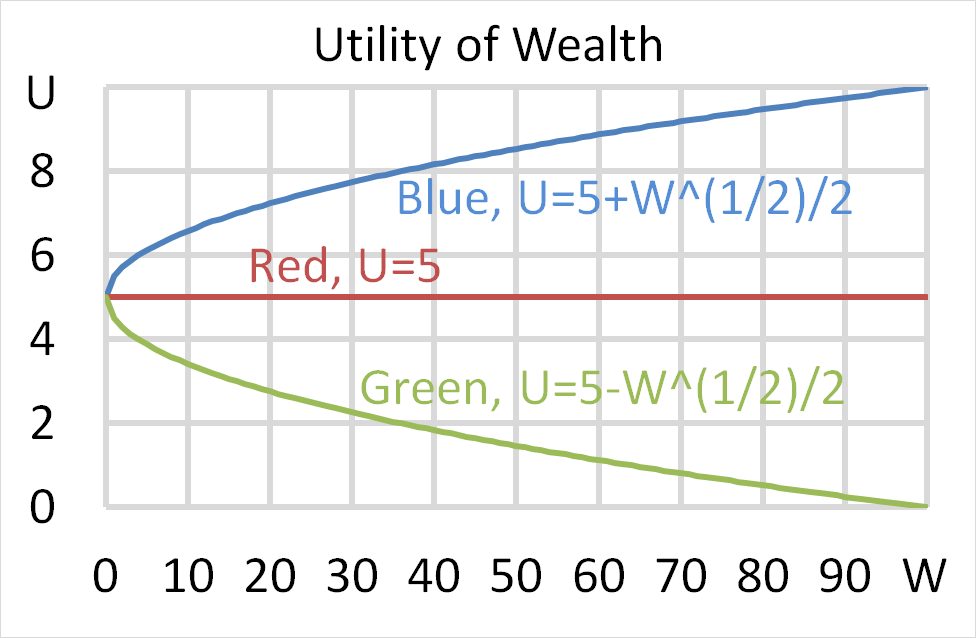
Question 700  utility, risk aversion, utility function, gamble

Mr Blue, Miss Red and Mrs Green are people with different utility functions.

Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

(a) Mr Blue's expected utility of wealth from gambling is 7.5 while refusing is 8.54. So the gamble makes him less happy.

(b) Miss Red's expected utility of wealth from gambling is 5 and refusing is also 5. So the gamble doesn't affect her happiness at all.

(c) Mr Blue's certainty equivalent of the risky gamble is $25. This is less than his current wealth which is why he would refuse.

(d) Miss Red's certainty equivalent of the risky gamble is any wealth. She's indifferent since she always has the same level of happiness.

(e) Mrs Green's certainty equivalent of the risky gamble is $25. This is less than her current wealth which is why she would refuse.

Question 735  debt terminology

You deposit money into a bank. Which of the following statements is NOT correct? You:

(a) Are a lender.

(b) Issued debt.

(c) Bought debt.

(d) Are a debt holder.

(e) Own a debt asset.

Question 753  NPV, perpetuity, DDM

The following cash flows are expected:

• A perpetuity of yearly payments of $30, with the first payment in 5 years (first payment at t=5, which continues every year after that forever).
• One payment of $100 in 6 years and 3 months (t=6.25).

What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?

(a) $260.022324

(b) $213.660269

(c) $178.949525

(d) $151.628987

(e) $140.71319

Question 879  margin loan, Basel accord

The risk-weight on "Margin lending against listed instruments on recognised exchanges" is 20% according to APRA's interpretation of the Basel 3 Accord in 'Prudential Standard APS 112 Capital Adequacy: Standardised Approach to Credit Risk, Attachment A: Risk-weights for on-balance sheet assets'.

A bank is considering lending a $100,000 margin loan secured by an ASX-listed stock. How much regulatory capital will the bank require to grant this loan under the Basel 3 Accord? Ignore the capital conservation buffer and the off-balance sheet exposure.

(a) $100,000.

(b) $28,000.

(c) $20,000.

(d) $8,000.

(e) $1,600.