Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
Stock A and B's returns have a correlation of 0.3. Which statement is NOT correct?
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
Question 104 CAPM, payout policy, capital structure, Miller and Modigliani, risk
Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.
For a firm operating in this perfect world, which statement(s) are correct?
(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.
(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.
(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.
Select the most correct response:
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A very low-risk stock just paid its semi-annual dividend of $0.14, as it has for the last 5 years. You conservatively estimate that from now on the dividend will fall at a rate of 1% every 6 months.
If the stock currently sells for $3 per share, what must be its required total return as an effective annual rate?
If risk free government bonds are trading at a yield of 4% pa, given as an effective annual rate, would you consider buying or selling the stock?
The stock's required total return is:
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
Diversification in a portfolio of two assets works best when the correlation between their returns is:
Question 244 CAPM, SML, NPV, risk
Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:
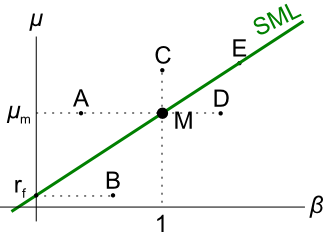
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?
Question 271 CAPM, option, risk, systematic risk, systematic and idiosyncratic risk
All things remaining equal, according to the capital asset pricing model, if the systematic variance of an asset increases, its required return will increase and its price will decrease.
If the idiosyncratic variance of an asset increases, its price will be unchanged.
What is the relationship between the price of a call or put option and the total, systematic and idiosyncratic variance of the underlying asset that the option is based on? Select the most correct answer.
Call and put option prices increase when the:
Find the sample standard deviation of returns using the data in the table:
| Stock Returns | |
| Year | Return pa |
| 2008 | 0.3 |
| 2009 | 0.02 |
| 2010 | -0.2 |
| 2011 | 0.4 |
The returns above and standard deviations below are given in decimal form.
Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.
What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
Let the variance of returns for a share per month be ##\sigma_\text{monthly}^2##.
What is the formula for the variance of the share's returns per year ##(\sigma_\text{yearly}^2)##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
Question 308 risk, standard deviation, variance, no explanation
A stock's standard deviation of returns is expected to be:
- 0.09 per month for the first 5 months;
- 0.14 per month for the next 7 months.
What is the expected standard deviation of the stock per year ##(\sigma_\text{annual})##?
Assume that returns are independently and identically distributed (iid) and therefore have zero auto-correlation.
The accounting identity states that the book value of a company's assets (A) equals its liabilities (L) plus owners equity (OE), so A = L + OE.
The finance version states that the market value of a company's assets (V) equals the market value of its debt (D) plus equity (E), so V = D + E.
Therefore a business's assets can be seen as a portfolio of the debt and equity that fund the assets.
Let ##\sigma_\text{V total}^2## be the total variance of returns on assets, ##\sigma_\text{V syst}^2## be the systematic variance of returns on assets, and ##\sigma_\text{V idio}^2## be the idiosyncratic variance of returns on assets, and ##\rho_\text{D idio, E idio}## be the correlation between the idiosyncratic returns on debt and equity.
Which of the following equations is NOT correct?
High risk firms in danger of bankruptcy tend to have:
Question 524 risk, expected and historical returns, bankruptcy or insolvency, capital structure, corporate financial decision theory, limited liability
Which of the following statements is NOT correct?
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
A stock's required total return will increase when its:
An economy has only two investable assets: stocks and cash.
Stocks had a historical nominal average total return of negative two percent per annum (-2% pa) over the last 20 years. Stocks are liquid and actively traded. Stock returns are variable, they have risk.
Cash is riskless and has a nominal constant return of zero percent per annum (0% pa), which it had in the past and will have in the future. Cash can be kept safely at zero cost. Cash can be converted into shares and vice versa at zero cost.
The nominal total return of the shares over the next year is expected to be:
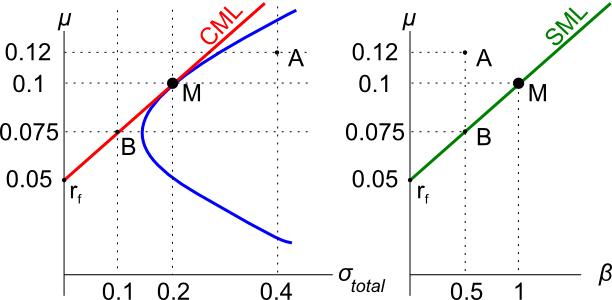
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
Which of the following is NOT a valid method for estimating the beta of a company's stock? Assume that markets are efficient, a long history of past data is available, the stock possesses idiosyncratic and market risk. The variances and standard deviations below denote total risks.
Question 800 leverage, portfolio return, risk, portfolio risk, capital structure, no explanation
Which of the following assets would you expect to have the highest required rate of return? All values are current market values.
Which of the following statements about an asset’s standard deviation of returns is NOT correct? All other things remaining equal, the higher the asset’s standard deviation of returns:
Question 988 variance, covariance, beta, CAPM, risk, no explanation
| Price Data Time Series | |||||||||||
| Sourced from Yahoo Finance Historical Price Data | |||||||||||
| Date | S&P500 Index (^GSPC) | Apple (AAPL) | |||||||||
| Open | High | Low | Close | Adj close | Open | High | Low | Close | Adj close | ||
| 2007, Wed 3 Jan | 1418 | 1429 | 1408 | 1417 | 1417 | 12.33 | 12.37 | 11.7 | 11.97 | 10.42 | |
| 2008, Wed 2 Jan | 1468 | 1472 | 1442 | 1447 | 1447 | 28.47 | 28.61 | 27.51 | 27.83 | 24.22 | |
| 2009, Fri 2 Jan | 903 | 935 | 899 | 932 | 932 | 12.27 | 13.01 | 12.17 | 12.96 | 11.28 | |
| 2010, Mon 4 Jan | 1117 | 1134 | 1117 | 1133 | 1133 | 30.49 | 30.64 | 30.34 | 30.57 | 26.6 | |
| Source: Yahoo Finance. | |||||||||||
Which of the following statements about the above table which is used to calculate Apple's equity beta is NOT correct?
Question 1003 Black-Scholes-Merton option pricing, log-normal distribution, return distribution, hedge fund, risk, financial distress
A hedge fund issued zero coupon bonds with a combined $1 billion face value due to be paid in 3 years. The promised yield to maturity is currently 6% pa given as a continuously compounded return (or log gross discrete return, ##LGDR=\ln[P_T/P_0] \div T##).
The hedge fund owns stock assets worth $1.1 billion now which are expected to have a 10% pa arithmetic average log gross discrete return ##(\text{AALGDR} = \sum\limits_{t=1}^T{\left( \ln[P_t/P_{t-1}] \right)} \div T)## and 30pp pa standard deviation (SDLGDR) in the future.
Analyse the hedge fund using the Merton model of corporate equity as an option on the firm's assets.
The risk free government bond yield to maturity is currently 5% pa given as a continuously compounded return or LGDR.
Which of the below statements is NOT correct? All figures are rounded to the sixth decimal place.