You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just agreed to a 30 year fully amortising mortgage loan with monthly payments of $2,500. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change. The below choices are given in the same order.
You want to buy a house priced at $400,000. You have saved a deposit of $40,000. The bank has agreed to lend you $360,000 as a fully amortising loan with a term of 30 years. The interest rate is 8% pa payable monthly and is not expected to change.
What will be your monthly payments?
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
You want to buy an apartment worth $300,000. You have saved a deposit of $60,000.
The bank has agreed to lend you $240,000 as an interest only mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
A prospective home buyer can afford to pay $2,000 per month in mortgage loan repayments. The central bank recently lowered its policy rate by 0.25%, and residential home lenders cut their mortgage loan rates from 4.74% to 4.49%.
How much more can the prospective home buyer borrow now that interest rates are 4.49% rather than 4.74%? Give your answer as a proportional increase over the original amount he could borrow (##V_\text{before}##), so:
###\text{Proportional increase} = \frac{V_\text{after}-V_\text{before}}{V_\text{before}} ###Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates compounding per month.
Many Australian home loans that are interest-only actually require payments to be made on a fully amortising basis after a number of years.
You decide to borrow $600,000 from the bank at an interest rate of 4.25% pa for 25 years. The payments will be interest-only for the first 10 years (t=0 to 10 years), then they will have to be paid on a fully amortising basis for the last 15 years (t=10 to 25 years).
Assuming that interest rates will remain constant, what will be your monthly payments over the first 10 years from now, and then the next 15 years after that? The answer options are given in the same order.
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 4% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
Telsa Motors advertises that its Model S electric car saves $570 per month in fuel costs. Assume that Tesla cars last for 10 years, fuel and electricity costs remain the same, and savings are made at the end of each month with the first saving of $570 in one month from now.
The effective annual interest rate is 15.8%, and the effective monthly interest rate is 1.23%. What is the present value of the savings?
You are promised 20 payments of $100, where the first payment is immediate (t=0) and the last is at the end of the 19th year (t=19). The effective annual discount rate is ##r##.
Which of the following equations does NOT give the correct present value of these 20 payments?
You deposit money into a bank. Which of the following statements is NOT correct? You:
You bought a house, primarily funded using a home loan from a bank. Which of the following statements is NOT correct?
Question 771 debt terminology, interest expense, interest tax shield, credit risk, no explanation
You deposit money into a bank account. Which of the following statements about this deposit is NOT correct?
By convention, money market securities' yields are always quoted as:
Which of the following statements is NOT correct? Money market securities are:
A 90-day Bank Accepted Bill (BAB) has a face value of $1,000,000. The simple interest rate is 10% pa and there are 365 days in the year. What is its price now?
Question 327 bill pricing, simple interest rate, no explanation
On 27/09/13, three month Swiss government bills traded at a yield of -0.2%, given as a simple annual yield. That is, interest rates were negative.
If the face value of one of these 90 day bills is CHF1,000,000 (CHF represents Swiss Francs, the Swiss currency), what is the price of one of these bills?
A bank bill was bought for $99,000 and sold for $100,000 thirty (30) days later. There are 365 days in the year. Which of the following formulas gives the simple interest rate per annum over those 30 days?
Note: To help you identify which is the correct answer without doing any calculations yourself, the formulas used to calculate the numbers are given.
A 90 day bank bill has a face value of $100,000.
Investor A bought the bill when it was first issued at a simple yield to maturity of 3% pa and sold it 20 days later to Investor B who expected to earn a simple yield to maturity of 5% pa. Investor B held it until maturity.
Which of the following statements is NOT correct?
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
Question 408 leverage, portfolio beta, portfolio risk, real estate, CAPM
You just bought a house worth $1,000,000. You financed it with an $800,000 mortgage loan and a deposit of $200,000.
You estimate that:
- The house has a beta of 1;
- The mortgage loan has a beta of 0.2.
What is the beta of the equity (the $200,000 deposit) that you have in your house?
Also, if the risk free rate is 5% pa and the market portfolio's return is 10% pa, what is the expected return on equity in your house? Ignore taxes, assume that all cash flows (interest payments and rent) were paid and received at the end of the year, and all rates are effective annual rates.
Question 800 leverage, portfolio return, risk, portfolio risk, capital structure, no explanation
Which of the following assets would you expect to have the highest required rate of return? All values are current market values.
A firm has a debt-to-equity ratio of 25%. What is its debt-to-assets ratio?
A firm has a debt-to-equity ratio of 60%. What is its debt-to-assets ratio?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?
You may assume:
- the value of debt (D) is constant through time,
- The cost of debt and the yield on debt are equal and given by ##r_D##.
- the appropriate rate to discount interest tax shields is ##r_D##.
- ##\text{IntExp}=D.r_D##
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.
For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.
The advantage of negative gearing is an example of the benefits of:
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Question 941 negative gearing, leverage, capital structure, interest tax shield, real estate
Last year, two friends Lev and Nolev each bought similar investment properties for $1 million. Both earned net rents of $30,000 pa over the past year. They funded their purchases in different ways:
- Lev used $200,000 of his own money and borrowed $800,000 from the bank in the form of an interest-only loan with an interest rate of 5% pa.
- Nolev used $1,000,000 of his own money, he has no mortgage loan on his property.
Both Lev and Nolev also work in high-paying jobs and are subject personal marginal tax rates of 45%.
Which of the below statements about the past year is NOT correct?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
Question 772 interest tax shield, capital structure, leverage
A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?
To receive the dividend you must own the stock when the market closes on which date?
On which date would the stock price increase if the dividend and earnings are higher than expected?
A company announces that it will pay a dividend, as the market expected. The company's shares trade on the stock exchange which is open from 10am in the morning to 4pm in the afternoon each weekday. When would the share price be expected to fall by the amount of the dividend? Ignore taxes.
The share price is expected to fall during the:
A company conducts a 4 for 3 stock split. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A firm conducts a two-for-one stock split. Which of the following consequences would NOT be expected?
In the dividend discount model (DDM), share prices fall when dividends are paid. Let the high price before the fall be called the peak, and the low price after the fall be called the trough.
###P_0=\dfrac{C_1}{r-g}###
Which of the following statements about the DDM is NOT correct?
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
A mature firm has constant expected future earnings and dividends. Both amounts are equal. So earnings and dividends are expected to be equal and unchanging.
Which of the following statements is NOT correct?
Which firms tend to have high forward-looking price-earnings (PE) ratios?
Treasury bonds currently have a return of 5% pa. A stock has a beta of 0.5 and the market return is 10% pa. What is the expected return of the stock?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the price of the stock now?
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
A stock's required total return will increase when its:
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
What do you think will be the stock's expected return over the next year, given as an effective annual rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
Over the last year, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. So ##r_{m} = (P_{0} - P_{-1})/P_{-1} = -0.01##, where the current time is zero and one year ago is time -1. The risk free rate was unchanged.
What do you think was the stock's historical return over the last year, given as an effective annual rate?
Question 807 market efficiency, expected and historical returns, CAPM, beta, systematic risk, no explanation
You work in Asia and just woke up. It looked like a nice day but then you read the news and found out that last night the American share market fell by 10% while you were asleep due to surprisingly poor macro-economic world news. You own a portfolio of liquid stocks listed in Asia with a beta of 1.6. When the Asian equity markets open, what do you expect to happen to your share portfolio? Assume that the capital asset pricing model (CAPM) is correct and that the market portfolio contains all shares in the world, of which American shares are a big part. Your portfolio beta is measured against this world market portfolio.
When the Asian equity market opens for trade, you would expect your portfolio value to:
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
Question 657 systematic and idiosyncratic risk, CAPM, no explanation
A stock's required total return will decrease when its:
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
Question 96 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds paying semi-annual coupons:
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
A European company just issued two bonds, a
- 3 year zero coupon bond at a yield of 6% pa, and a
- 4 year zero coupon bond at a yield of 6.5% pa.
What is the company's forward rate over the fourth year (from t=3 to t=4)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 25 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 2 year zero coupon bond at a yield of 8% pa, and a
- 3 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 108 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 1 year zero coupon bond at a yield of 10% pa, and
- A 2 year zero coupon bond at a yield of 8% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 143 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 6-month zero coupon bond at a yield of 6% pa, and
- A 12 month zero coupon bond at a yield of 7% pa.
What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 572 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Question 573 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, liquidity premium theory, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Question 693 boot strapping zero coupon yield, forward interest rate, term structure of interest rates
Information about three risk free Government bonds is given in the table below.
| Federal Treasury Bond Data | ||||
| Maturity | Yield to maturity | Coupon rate | Face value | Price |
| (years) | (pa, compounding semi-annually) | (pa, paid semi-annually) | ($) | ($) |
| 0.5 | 3% | 4% | 100 | 100.4926 |
| 1 | 4% | 4% | 100 | 100.0000 |
| 1.5 | 5% | 4% | 100 | 98.5720 |
Based on the above government bonds' yields to maturity, which of the below statements about the spot zero rates and forward zero rates is NOT correct?
Question 784 boot strapping zero coupon yield, forward interest rate, term structure of interest rates
Information about three risk free Government bonds is given in the table below.
| Federal Treasury Bond Data | ||||
| Maturity | Yield to maturity | Coupon rate | Face value | Price |
| (years) | (pa, compounding annually) | (pa, paid annually) | ($) | ($) |
| 1 | 0% | 2% | 100 | 102 |
| 2 | 1% | 2% | 100 | 101.9703951 |
| 3 | 2% | 2% | 100 | 100 |
Based on the above government bonds' yields to maturity, which of the below statements about the spot zero rates and forward zero rates is NOT correct?
A share was bought for $20 (at t=0) and paid its annual dividend of $3 one year later (at t=1). Just after the dividend was paid, the share price was $16 (at t=1). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
Which of the following statements about an asset’s standard deviation of returns is NOT correct? All other things remaining equal, the higher the asset’s standard deviation of returns:
Stock A and B's returns have a correlation of 0.3. Which statement is NOT correct?
The following table shows a sample of historical total returns of shares in two different companies A and B.
| Stock Returns | ||
| Total effective annual returns | ||
| Year | ##r_A## | ##r_B## |
| 2007 | 0.2 | 0.4 |
| 2008 | 0.04 | -0.2 |
| 2009 | -0.1 | -0.3 |
| 2010 | 0.18 | 0.5 |
What is the historical sample covariance (##\hat{\sigma}_{A,B}##) and correlation (##\rho_{A,B}##) of stock A and B's total effective annual returns?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the expected return of the above portfolio?
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
Diversification in a portfolio of two assets works best when the correlation between their returns is:
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Covariance ##(\sigma_{A,B})## | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the standard deviation (not variance) of the above portfolio? Note that the stocks' covariance is given, not correlation.
Question 558 portfolio weights, portfolio return, short selling
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 16% pa.
- Stock A has an expected return of 8% pa.
- Stock B has an expected return of 12% pa.
What portfolio weights should the investor have in stocks A and B respectively?
The standard deviation and variance of a stock's annual returns are calculated over a number of years. The units of the returns are percent per annum ##(\% pa)##.
What are the units of the standard deviation ##(\sigma)## and variance ##(\sigma^2)## of returns respectively?
Hint: Visit Wikipedia to understand the difference between percentage points ##(\text{pp})## and percent ##(\%)##.
A stock's returns are normally distributed with a mean of 10% pa and a standard deviation of 20 percentage points pa. What is the 90% confidence interval of returns over the next year? Note that the Z-statistic corresponding to a one-tail:
- 90% normal probability density function is 1.282.
- 95% normal probability density function is 1.645.
- 97.5% normal probability density function is 1.960.
The 90% confidence interval of annual returns is between:
A stock's returns are normally distributed with a mean of 10% pa and a standard deviation of 20 percentage points pa. What is the 95% confidence interval of returns over the next year? Note that the Z-statistic corresponding to a one-tail:
- 90% normal probability density function is 1.282.
- 95% normal probability density function is 1.645.
- 97.5% normal probability density function is 1.960.
The 95% confidence interval of annual returns is between:
A stock has an expected return of 10% pa and you're 90% sure that over the next year, the return will be between -15% and 35%. The stock's returns are normally distributed. Note that the Z-statistic corresponding to a one-tail:
- 90% normal probability density function is 1.282.
- 95% normal probability density function is 1.645.
- 97.5% normal probability density function is 1.960.
What is the stock’s standard deviation of returns in percentage points per annum (pp pa)?
Question 282 expected and historical returns, income and capital returns
You're the boss of an investment bank's equities research team. Your five analysts are each trying to find the expected total return over the next year of shares in a mining company. The mining firm:
- Is regarded as a mature company since it's quite stable in size and was floated around 30 years ago. It is not a high-growth company;
- Share price is very sensitive to changes in the price of the market portfolio, economic growth, the exchange rate and commodities prices. Due to this, its standard deviation of total returns is much higher than that of the market index;
- Experienced tough times in the last 10 years due to unexpected falls in commodity prices.
- Shares are traded in an active liquid market.
- The analysts' source data is correct and true, but their inferences might be wrong;
- All returns and yields are given as effective annual nominal rates.
Question 559 variance, standard deviation, covariance, correlation
Which of the following statements about standard statistical mathematics notation is NOT correct?
What is the covariance of a variable X with itself?
The cov(X, X) or ##\sigma_{X,X}## equals:
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
What is the covariance of a variable X with a constant C?
The cov(X, C) or ##\sigma_{X,C}## equals:
What is the correlation of a variable X with a constant C?
The corr(X, C) or ##\rho_{X,C}## equals:
Suppose you had $100 in a savings account and the interest rate was 2% per year.
After 5 years, how much do you think you would have in the account if you left the money to grow?
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Jan asks you for a loan. He wants $100 now and offers to pay you back $120 in 1 year. You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate.
Ignore credit risk. Remember:
### V_0 = \frac{V_t}{(1+r_\text{eff})^t} ###
Katya offers to pay you $10 at the end of every year for the next 5 years (t=1,2,3,4,5) if you pay her $50 now (t=0). You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate. Ignore credit risk.
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
For a price of $13, Carla will sell you a share paying a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $6, Carlos will sell you a share which will pay a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $102, Andrea will sell you a share which just paid a dividend of $10 yesterday, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##10(1+0.05)^1=$10.50## in one year from now, and the year after it will be ##10(1+0.05)^2=11.025## and so on.
The required return of the stock is 15% pa.
For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.
The required return of the stock is 15% pa.
For a price of $10.20 each, Renee will sell you 100 shares. Each share is expected to pay dividends in perpetuity, growing at a rate of 5% pa. The next dividend is one year away (t=1) and is expected to be $1 per share.
The required return of the stock is 15% pa.
For a price of $129, Joanne will sell you a share which is expected to pay a $30 dividend in one year, and a $10 dividend every year after that forever. So the stock's dividends will be $30 at t=1, $10 at t=2, $10 at t=3, and $10 forever onwards.
The required return of the stock is 10% pa.
For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.
The required return of the stock is 10% pa.
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.
For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $100, Andrea will sell you a 2 year bond paying annual coupons of 10% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
Suppose that the US government recently announced that subsidies for fresh milk producers will be gradually phased out over the next year. Newspapers say that there are expectations of a 40% increase in the spot price of fresh milk over the next year.
Option prices on fresh milk trading on the Chicago Mercantile Exchange (CME) reflect expectations of this 40% increase in spot prices over the next year. Similarly to the rest of the market, you believe that prices will rise by 40% over the next year.
What option trades are likely to be profitable, or to be more specific, result in a positive Net Present Value (NPV)?
Assume that:
- Only the spot price is expected to increase and there is no change in expected volatility or other variables that affect option prices.
- No taxes, transaction costs, information asymmetry, bid-ask spreads or other market frictions.
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
Question 625 dividend re-investment plan, capital raising
Which of the following statements about dividend re-investment plans (DRP's) is NOT correct?
Question 455 income and capital returns, payout policy, DDM, market efficiency
A fairly priced unlevered firm plans to pay a dividend of $1 next year (t=1) which is expected to grow by 3% pa every year after that. The firm's required return on equity is 8% pa.
The firm is thinking about reducing its future dividend payments by 10% so that it can use the extra cash to invest in more projects which are expected to return 8% pa, and have the same risk as the existing projects. Therefore, next year's dividend will be $0.90. No new equity or debt will be issued to fund the new projects, they'll all be funded by the cut in dividends.
What will be the stock's new annual capital return (proportional increase in price per year) if the change in payout policy goes ahead?
Assume that payout policy is irrelevant to firm value (so there's no signalling effects) and that all rates are effective annual rates.
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
Question 99 capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.
Assume that:
- The firm and individual investors can borrow at the same rate and have the same tax rates.
- The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
- There are no market frictions relating to debt such as asymmetric information or transaction costs.
- Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.
According to Miller and Modigliani's theory, which statement is correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
Question 237 WACC, Miller and Modigliani, interest tax shield
Which of the following discount rates should be the highest for a levered company? Ignore the costs of financial distress.
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Delta buys a future from Alice.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Delta buys a future from Bob.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Bob buys a future from Chris.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Alice, Bob, Chris and Delta are traders in the futures market. The following trades occur over a single day in a newly-opened equity index future that matures in one year which the exchange just made available.
1. Alice buys a future from Bob.
2. Chris buys a future from Delta.
3. Alice buys a future from Chris.
These were the only trades made in this equity index future. What was the trading volume and what is the open interest?
Question 397 financial distress, leverage, capital structure, NPV
A levered firm has a market value of assets of $10m. Its debt is all comprised of zero-coupon bonds which mature in one year and have a combined face value of $9.9m.
Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.
Therefore the current market capitalisation of debt ##(D_0)## is $9m and equity ##(E_0)## is $1m.
A new project presents itself which requires an investment of $2m and will provide a:
- $6.6m cash flow with probability 0.5 in the good state of the world, and a
- -$4.4m (notice the negative sign) cash flow with probability 0.5 in the bad state of the world.
The project can be funded using the company's excess cash, no debt or equity raisings are required.
What would be the new market capitalisation of equity ##(E_\text{0, with project})## if shareholders vote to proceed with the project, and therefore should shareholders proceed with the project?
In the home loan market, the acronym LVR stands for Loan to Valuation Ratio. If you bought a house worth one million dollars, partly funded by an $800,000 home loan, then your LVR was 80%. The LVR is equivalent to which of the following ratios?
A newly floated farming company is financed with senior bonds, junior bonds, cumulative non-voting preferred stock and common stock. The new company has no retained profits and due to floods it was unable to record any revenues this year, leading to a loss. The firm is not bankrupt yet since it still has substantial contributed equity (same as paid-up capital).
On which securities must it pay interest or dividend payments in this terrible financial year?
A highly levered risky firm is trying to raise more debt. The types of debt being considered, in no particular order, are senior bonds, junior bonds, bank accepted bills, promissory notes and bank loans.
Which of these forms of debt is the safest from the perspective of the debt investors who are thinking of investing in the firm's new debt?
You're considering making an investment in a particular company. They have preference shares, ordinary shares, senior debt and junior debt.
Which is the safest investment? Which has the highest expected returns?
Question 794 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the Delta of a European call option?
Where:
###d_1=\dfrac{\ln[S_0/K]+(r+\sigma^2/2).T)}{\sigma.\sqrt{T}}### ###d_2=d_1-\sigma.\sqrt{T}=\dfrac{\ln[S_0/K]+(r-\sigma^2/2).T)}{\sigma.\sqrt{T}}###Question 795 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the Delta of a European put option?
Question 954 option, at the money option
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.
Ignoring the costs of financial distress, which of the following statements is NOT correct:
Question 858 indirect security, intermediated finance, no explanation
Which of the following transactions involves an ‘indirect security’ using a ‘financial intermediary’?
Question 513 stock split, reverse stock split, stock dividend, bonus issue, rights issue
Which of the following statements is NOT correct?
Question 566 capital structure, capital raising, rights issue, on market repurchase, dividend, stock split, bonus issue
A company's share price fell by 20% and its number of shares rose by 25%. Assume that there are no taxes, no signalling effects and no transaction costs.
Which one of the following corporate events may have happened?
Question 245 foreign exchange rate, monetary policy, foreign exchange rate direct quote, no explanation
Investors expect Australia's central bank, the RBA, to leave the policy rate unchanged at their next meeting.
Then unexpectedly, the policy rate is reduced due to fears that Australia's GDP growth is slowing.
What do you expect to happen to Australia's exchange rate? Direct and indirect quotes are given from the perspective of an Australian.
The Australian dollar will:
Question 319 foreign exchange rate, monetary policy, American and European terms
Investors expect the Reserve Bank of Australia (RBA) to keep the policy rate steady at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 25 basis points due to fears that the economy is growing too fast and that inflation will be above their target rate of 2 to 3 per cent.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:
Question 320 foreign exchange rate, monetary policy, American and European terms
Investors expect the Reserve Bank of Australia (RBA) to decrease the overnight cash rate at their next meeting.
Then unexpectedly, the RBA announce that they will keep the policy rate unchanged.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:
Question 321 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 50 basis points due to high future GDP and inflation forecasts.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar will:
Question 322 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to decrease the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will decrease the policy rate by 50 basis points due to fears of a recession and deflation.
What do you expect to happen to Australia's exchange rate? The Australian dollar will:
Which Australian institution is in charge of monetary policy?
The Australian central bank implements monetary policy by directly controlling which interest rate?
Below is the Australian central bank’s cash rate.
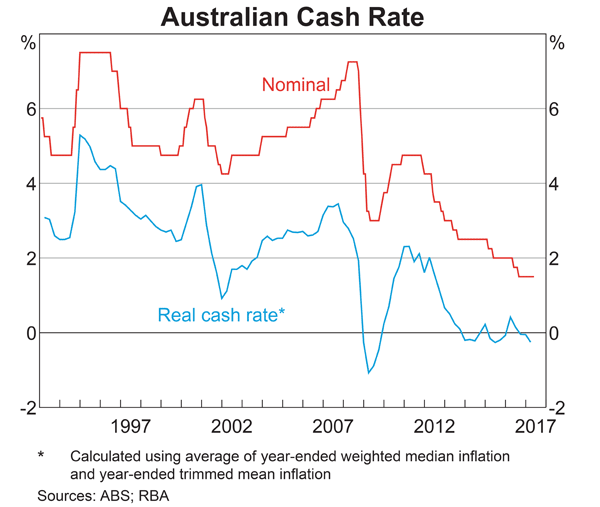
From 2011 to 2017 the Australian central bank has implemented:
Below is the Australian federal government’s budget balance as a percent of GDP. Note that the columns to the right of the vertical black line were a forecast at the time. The x-axis shows financial years, so for example the 06/07 financial year represents the time period from 1 July 2006 to 30 June 2007.
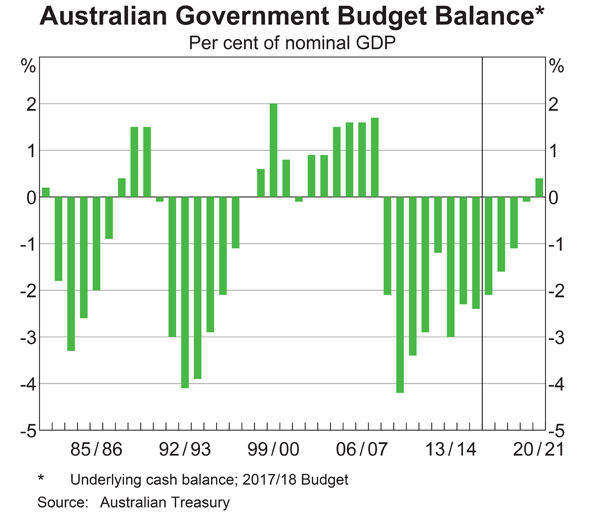
Comparing the 2008/09 financial year to the previous one, the Australian federal government implemented:
Which of the following is NOT the Australian central bank’s responsibility?
Question 862 yield curve, bond pricing, bill pricing, monetary policy, no explanation
Refer to the below graph when answering the questions.
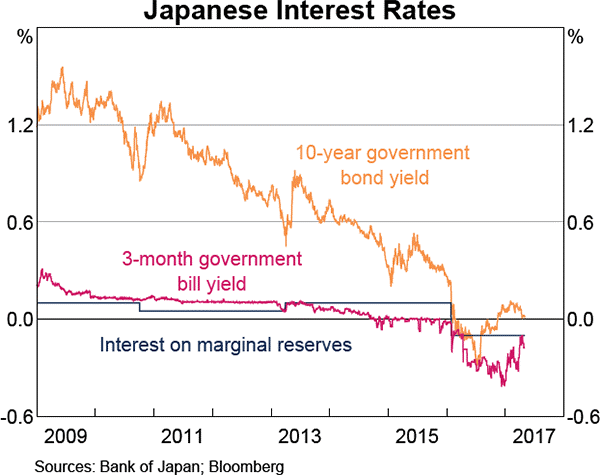
Which of the following statements is NOT correct?
Question 883 monetary policy, impossible trinity, foreign exchange rate
It’s often thought that the ideal currency or exchange rate regime would:
1. Be fixed against the USD;
2. Be convertible to and from USD for traders and investors so there are open goods, services and capital markets, and;
3. Allow independent monetary policy set by the country’s central bank, independent of the US central bank. So the country can set its own interest rate independent of the US Federal Reserve’s USD interest rate.
However, not all of these characteristics can be achieved. One must be sacrificed. This is the 'impossible trinity'.
Which of the following exchange rate regimes sacrifices convertibility?
Question 884 monetary policy, impossible trinity, foreign exchange rate, no explanation
According to the impossible trinity, a currency can only have two of these three desirable traits: be fixed against the USD; convertible to and from USD for traders and investors so there are open goods, services and capital markets; and allow independent monetary policy set by the country’s central bank, independent of the US central bank.
Which of the following exchange rate regimes sacrifices fixing the exchange rate to the USD? In other words, which regime uses a floating exchange rate?
Question 890 foreign exchange rate, monetary policy, no explanation
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting. The current exchange rate is 0.8 USD per AUD.
Then unexpectedly, the RBA announce that they will increase the policy rate by 50 basis points due to increased fears of inflation.
What do you expect to happen to Australia's exchange rate on the day when the surprise announcement is made? The Australian dollar is likely to suddenly:
Question 891 foreign exchange rate, monetary policy, no explanation
Suppose the market expects the Bank of Japan (BoJ) to decrease their short term interest rate by 15 basis points at their next meeting. The current short term interest rate is -0.1% pa and the exchange rate is 100 JPY per USD.
Then unexpectedly, the BoJ announce that they will leave the short term interest rate unchanged.
What do you expect to happen to Japan’s exchange rate on the day when the surprise announcement is made? The Japanese Yen (JPY) is likely to suddenly:
Question 882 Asian currency crisis, foreign exchange rate, original sin, no explanation
In the 1997 Asian currency crisis, the businesses most vulnerable to bankruptcy were those that:
The risk-weight on "Margin lending against listed instruments on recognised exchanges" is 20% according to APRA's interpretation of the Basel 3 Accord in 'Prudential Standard APS 112 Capital Adequacy: Standardised Approach to Credit Risk, Attachment A: Risk-weights for on-balance sheet assets'.
A bank is considering lending a $100,000 margin loan secured by an ASX-listed stock. How much regulatory capital will the bank require to grant this loan under the Basel 3 Accord? Ignore the capital conservation buffer and the off-balance sheet exposure.
Which of the following statements about the Basel 3 minimum capital requirements is NOT correct? Common equity tier 1 (CET1) comprises the highest quality components of capital that fully satisfy all of the following characteristics:
The below graph from the RBA shows the phase-in of the Basel 3 minimum regulatory capital requirements under the Basel Committee on Banking Supervision (BCBS) on the left panel and in Australia under the Australian Prudential Regulatory Authority (APRA) on the right panel.
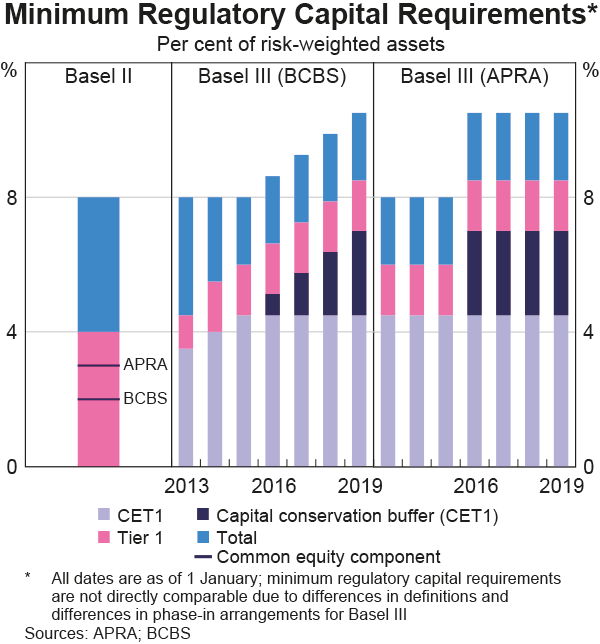
Which of the following statements about the Basel 3 minimum regulatory capital requirements as at 2019 is NOT correct? All minimum amounts exclude the 2.5% counter-cyclical buffer.
The Basel 3 minimum regulatory capital requirement as a percent of Risk Weighted Assets (RWA) is:
Below is a table of the 'Risk-weights for residential mortgages' as shown in APRA Basel 3 Prudential Standard APS 112 Capital Adequacy: Standardised Approach to Credit Risk January 2013.
| LVR (%) |
Standard eligible mortgages |
Non-standard eligible mortgages |
||
|
|
Risk-weight (no mortgage insurance) % |
Risk-weight (with at least 40% of the mortgage insured by an acceptable LMI) % |
Risk-weight (no mortgage insurance) % |
Risk-weight (with at least 40% of the mortgage insured by an acceptable LMI) % |
| 0 – 60 |
35 |
35 |
50 |
35 |
| 60.01 – 80 |
35 |
35 |
75 |
50 |
| 80.01 – 90 |
50 |
35 |
100 |
75 |
| 90.01 – 100 |
75 |
50 |
100 |
75 |
| > 100.01 |
100 |
75 |
100 |
100 |
A bank is considering granting a home loan to a man to buy a house worth $1.25 million using his own funds and the loan. The loan would be standard with no lenders mortgage insurance (LMI) and an LVR of 80%.
What is the minimum regulatory capital that the bank requires to grant the home loan under the Basel 3 Accord? Ignore the capital conservation buffer.
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
Question 859 money supply, no explanation
The below table shows Australian monetary aggregates. Note that ‘M3’ is the sum of all the figures in the table and ‘ADI’ stands for Authorised Deposit-taking Institution such as a bank, building society or credit union.
| Australian Monetary Aggregates | ||||||
| March 2017, AUD billions | ||||||
| Currency | Current deposits with banks |
Certificates of deposit issued by banks |
Term deposits with banks |
Other deposits with banks |
Deposits with non-bank ADIs |
M3 |
| 69.3 | 271.6 | 207.2 | 562.3 | 838.7 | 36.9 | 1986.0 |
Source: RBA Statistical Table D3 Monetary Aggregates.
Which of the following statements is NOT correct?
The DuPont formula is:
###\dfrac{\text{Net Profit}}{\text{Sales}} \times \dfrac{\text{Sales}}{\text{Total Assets}} \times \dfrac{\text{Total Assets}}{\text{Owners' Equity}}###
Which of the following statements about the DuPont formula is NOT correct?
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Itau Unibanco is a major listed bank in Brazil with a market capitalisation of equity equal to BRL 85.744 billion, EPS of BRL 3.96 and 2.97 billion shares on issue.
Banco Bradesco is another major bank with total earnings of BRL 8.77 billion and 2.52 billion shares on issue.
Estimate Banco Bradesco's current share price using a price-earnings multiples approach assuming that Itau Unibanco is a comparable firm.
Note that BRL is the Brazilian Real, their currency. Figures sourced from Google Finance on the market close of the BVMF on 24 July 2015.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Question 749 Multiples valuation, PE ratio, price to revenue ratio, price to book ratio, NPV
A real estate agent says that the price of a house in Sydney Australia is approximately equal to the gross weekly rent times 1000.
What type of valuation method is the real estate agent using?
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
The below diagram shows a firm’s cash cycle.
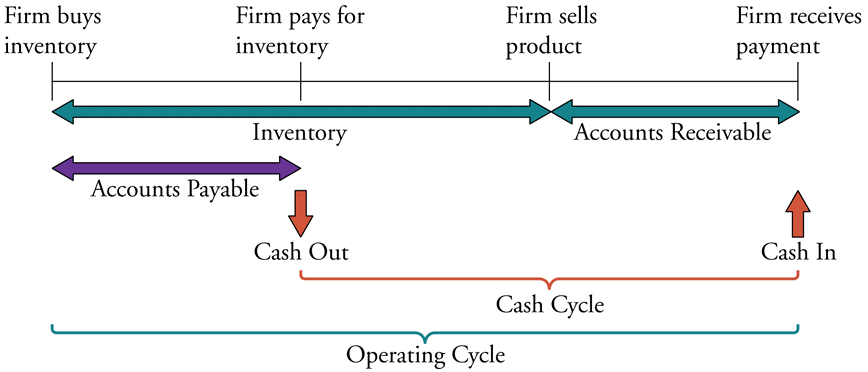
Which of the following statements about companies’ cash cycle is NOT correct?
What is the Cash Conversion Cycle for a firm with a:
- Payables period of 1 day;
- Inventory period of 50 days; and
- Receivables period of 30 days?
All answer options are in days:
Question 959 negative gearing, leverage, capital structure, interest tax shield, real estate
Last year, two friends Gear and Nogear invested in residential apartments. Each invested $1 million of their own money (their net wealth).
Apartments cost $1,000,000 last year and they earned net rents of $30,000 pa over the last year. Net rents are calculated as rent revenues less the costs of renting such as property maintenance, land tax and council rates. However, interest expense and personal income taxes are not deducted from net rents.
Gear and Nogear funded their purchases in different ways:
- Gear used $1,000,000 of her own money and borrowed $4,000,000 from the bank in the form of an interest-only loan with an interest rate of 5% pa to buy 5 apartments.
- Nogear used $1,000,000 of his own money to buy one apartment. He has no mortgage loan on his property.
Both Gear and Nogear also work in high-paying jobs and are subject personal marginal tax rates of 45%.
Which of the below statements about the past year is NOT correct?
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use net operating profit after tax (NOPAT).
###\begin{aligned} FFCF &= NOPAT + Depr - CapEx -\Delta NWC \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC \\ \end{aligned} \\###
One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.
Which of the below FFCF formulas include the interest tax shield in the cash flow?
###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
There are many different ways to value a firm's assets. Which of the following will NOT give the correct market value of a levered firm's assets ##(V_L)##? Assume that:
- The firm is financed by listed common stock and vanilla annual fixed coupon bonds, which are both traded in a liquid market.
- The bonds' yield is equal to the coupon rate, so the bonds are issued at par. The yield curve is flat and yields are not expected to change. When bonds mature they will be rolled over by issuing the same number of new bonds with the same expected yield and coupon rate, and so on forever.
- Tax rates on the dividends and capital gains received by investors are equal, and capital gains tax is paid every year, even on unrealised gains regardless of when the asset is sold.
- There is no re-investment of the firm's cash back into the business. All of the firm's excess cash flow is paid out as dividends so real growth is zero.
- The firm operates in a mature industry with zero real growth.
- All cash flows and rates in the below equations are real (not nominal) and are expected to be stable forever. Therefore the perpetuity equation with no growth is suitable for valuation.
Where:
###r_\text{WACC before tax} = r_D.\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital before tax}### ###r_\text{WACC after tax} = r_D.(1-t_c).\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital after tax}### ###NI_L=(Rev-COGS-FC-Depr-\mathbf{IntExp}).(1-t_c) = \text{Net Income Levered}### ###CFFA_L=NI_L+Depr-CapEx - \varDelta NWC+\mathbf{IntExp} = \text{Cash Flow From Assets Levered}### ###NI_U=(Rev-COGS-FC-Depr).(1-t_c) = \text{Net Income Unlevered}### ###CFFA_U=NI_U+Depr-CapEx - \varDelta NWC= \text{Cash Flow From Assets Unlevered}###Read the following financial statements and calculate the firm's free cash flow over the 2014 financial year.
| UBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2014 | ||
| $m | ||
| Sales | 293 | |
| COGS | 200 | |
| Rent expense | 15 | |
| Gas expense | 8 | |
| Depreciation | 10 | |
| EBIT | 60 | |
| Interest expense | 0 | |
| Taxable income | 60 | |
| Taxes | 18 | |
| Net income | 42 | |
| UBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2014 | 2013 |
| $m | $m | |
| Assets | ||
| Cash | 30 | 29 |
| Accounts receivable | 5 | 7 |
| Pre-paid rent expense | 1 | 0 |
| Inventory | 50 | 46 |
| PPE | 290 | 300 |
| Total assets | 376 | 382 |
| Liabilities | ||
| Trade payables | 20 | 18 |
| Accrued gas expense | 3 | 2 |
| Non-current liabilities | 0 | 0 |
| Contributed equity | 212 | 212 |
| Retained profits | 136 | 150 |
| Asset revaluation reserve | 5 | 0 |
| Total L and OE | 376 | 382 |
Note: all figures are given in millions of dollars ($m).
The firm's free cash flow over the 2014 financial year was:
The saying "buy low, sell high" suggests that investors should make a:
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
Total cash flows can be broken into income and capital cash flows. What is the name given to the income cash flow from owning shares?
Which of the following equations is NOT equal to the total return of an asset?
Let ##p_0## be the current price, ##p_1## the expected price in one year and ##c_1## the expected income in one year.
A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).
What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
A share was bought for $30 (at t=0) and paid its annual dividend of $6 one year later (at t=1).
Just after the dividend was paid, the share price fell to $27 (at t=1). What were the total, capital and income returns given as effective annual rates?
The choices are given in the same order:
##r_\text{total}## , ##r_\text{capital}## , ##r_\text{dividend}##.
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
An Apple (NASDAQ:AAPL) stock was purchased by an investor for $120 and one year later was sold for $150. A dividend of $4 was also collected at the end of the year just before the stock was sold.
Which of the following statements about the stock investment is NOT correct? Ignore taxes.
Over the year, the investor made a:
.
Question 915 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For a share price to double over 7 years, what must its capital return be as an effective annual rate?
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
A one year European-style call option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The call option price now is:
A one year European-style put option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The put option price now is:
A 12 month European-style call option with a strike price of $11 is written on a dividend paying stock currently trading at $10. The dividend is paid annually and the next dividend is expected to be $0.40, paid in 9 months. The risk-free interest rate is 5% pa continuously compounded and the standard deviation of the stock’s continuously compounded returns is 30 percentage points pa. The stock's continuously compounded returns are normally distributed. Using the Black-Scholes-Merton option valuation model, determine which of the following statements is NOT correct.
A one year European-style call option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
A one year European-style put option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The put option price now is:
Question 803 capital raising, rights issue, initial public offering, on market repurchase, no explanation
Which one of the following capital raisings or payouts involve the sale of shares to existing shareholders only?
A company conducts a 2 for 3 rights issue at a subscription price of $8 when the pre-announcement stock price was $9. Assume that all investors use their rights to buy those extra shares.
What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A firm is about to conduct a 2-for-7 rights issue with a subscription price of $10 per share. They haven’t announced the capital raising to the market yet and the share price is currently $13 per share. Assume that every shareholder will exercise their rights, the cash raised will simply be put in the bank, and the rights issue is completed so quickly that the time value of money can be ignored. Disregard signalling, taxes and agency-related effects.
Which of the following statements about the rights issue is NOT correct? After the rights issue is completed:
A firm wishes to raise $30 million now. The firm's current market value of equity is $60m and the market price per share is $20. They estimate that they'll be able to issue shares in a rights issue at a subscription price of $15. Ignore the time value of money and assume that all shareholders exercise their rights. Which of the following statements is NOT correct?
Question 568 rights issue, capital raising, capital structure
A company conducts a 1 for 5 rights issue at a subscription price of $7 when the pre-announcement stock price was $10. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order. Ignore all taxes, transaction costs and signalling effects.
Question 989 PE ratio, Multiples valuation, leverage, accounting ratio
A firm has 20 million stocks, earnings (or net income) of $100 million per annum and a 60% debt-to-equity ratio where both the debt and asset values are market values rather than book values. Similar firms have a PE ratio of 12.
Which of the below statements is NOT correct based on a PE multiples valuation?
Question 990 Multiples valuation, EV to EBITDA ratio, enterprise value
A firm has:
2 million shares;
$200 million EBITDA expected over the next year;
$100 million in cash (not included in EV);
1/3 market debt-to-assets ratio is (market assets = EV + cash);
4% pa expected dividend yield over the next year, paid annually with the next dividend expected in one year;
2% pa expected dividend growth rate;
40% expected payout ratio over the next year;10 times EV/EBITDA ratio.
30% corporate tax rate.
The stock can be valued using the EV/EBITDA multiple, dividend discount model, Gordon growth model or PE multiple. Which of the below statements is NOT correct based on an EV/EBITDA multiple valuation?
Which business structure or structures have the advantage of limited liability for equity investors?
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
Which one of the following businesses is likely to be a public company in Australia, judging by its name?
Question 452 limited liability, expected and historical returns
What is the lowest and highest expected share price and expected return from owning shares in a company over a finite period of time?
Let the current share price be ##p_0##, the expected future share price be ##p_1##, the expected future dividend be ##d_1## and the expected return be ##r##. Define the expected return as:
##r=\dfrac{p_1-p_0+d_1}{p_0} ##
The answer choices are stated using inequalities. As an example, the first answer choice "(a) ##0≤p<∞## and ##0≤r< 1##", states that the share price must be larger than or equal to zero and less than positive infinity, and that the return must be larger than or equal to zero and less than one.
A firm changes its capital structure by issuing a large amount of equity and using the funds to repay debt. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
In the dividend discount model:
###P_0 = \dfrac{C_1}{r-g}###
The return ##r## is supposed to be the:
In the dividend discount model:
### P_0= \frac{d_1}{r-g} ###
The pronumeral ##g## is supposed to be the:
Question 524 risk, expected and historical returns, bankruptcy or insolvency, capital structure, corporate financial decision theory, limited liability
Which of the following statements is NOT correct?
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Question 801 negative gearing, leverage, capital structure, no explanation
The following steps set out the process of ‘negative gearing’ an investment property in Australia. Which of these steps or statements is NOT correct? To successfully achieve negative gearing on an investment property:
Question 802 negative gearing, leverage, capital structure, no explanation
Which of the following statements about ‘negative gearing’ is NOT correct?
Which of the following statements about Macaulay duration is NOT correct? The Macaulay duration:
Find the Macaulay duration of a 2 year 5% pa annual fixed coupon bond which has a $100 face value and currently has a yield to maturity of 8% pa. The Macaulay duration is:
Find the Macaulay duration of a 2 year 5% pa semi-annual fixed coupon bond which has a $100 face value and currently has a yield to maturity of 8% pa. The Macaulay duration is:
Question 871 duration, Macaulay duration, modified duration, portfolio duration
Which of the following statements about Macaulay duration is NOT correct? The Macaulay duration:
Question 872 duration, Macaulay duration, modified duration, portfolio duration
A fixed coupon bond’s modified duration is 20 years, and yields are currently 10% pa compounded annually. Which of the following statements about the bond is NOT correct?
Question 918 duration, Macaulay duration, modified duration, bond convexity
A fixed coupon bond’s modified duration is 10 years, and yields are currently 5% pa compounded annually. Which of the following statements about the bond is NOT correct?
Which of the following statements about bond convexity is NOT correct?
Assume that the market portfolio has a duration of 15 years and an individual stock has a duration of 20 years.
What can you say about the stock's (single factor CAPM) beta with respect to the market portfolio? The stock's beta is likely to be:
Question 999 duration, duration of a perpetuity with growth, CAPM, DDM
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the Macaulay duration of the stock now?
Question 1000 duration, duration of a perpetuity with growth, needs refinement
An unlevered firm cuts its dividends and re-invests in zero-NPV projects with the same risk as its existing projects. This decreases the dividend yield, but increases the firm's equity's dividend growth rate and duration, while its total required return on equity remains unchanged. The equity can be valued as a perpetuity and the duration of a perpetuity is given below:
###D_\text{Macaulay} = \dfrac{1+r}{r-g}###What will be the effect on the stock's CAPM beta? Assume that there's no change in the risk free rate or market risk premium. The company's equity beta will:
Question 796 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European call option will be exercised?
Question 797 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European put option will be exercised?
Question 904 option, Black-Scholes-Merton option pricing, option on future on stock index
A six month European-style call option on six month S&P500 index futures has a strike price of 2800 points.
The six month futures price on the S&P500 index is currently at 2740.805274 points. The futures underlie the call option.
The S&P500 stock index currently trades at 2700 points. The stock index underlies the futures. The stock index's standard deviation of continuously compounded returns is 25% pa.
The risk-free interest rate is 5% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
Question 385 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The levered equity graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?
Question 707 continuously compounding rate, continuously compounding rate conversion
Convert a 10% effective annual rate ##(r_\text{eff annual})## into a continuously compounded annual rate ##(r_\text{cc annual})##. The equivalent continuously compounded annual rate is:
Question 708 continuously compounding rate, continuously compounding rate conversion
Convert a 10% continuously compounded annual rate ##(r_\text{cc annual})## into an effective annual rate ##(r_\text{eff annual})##. The equivalent effective annual rate is:
Which of the following interest rate quotes is NOT equivalent to a 10% effective annual rate of return? Assume that each year has 12 months, each month has 30 days, each day has 24 hours, each hour has 60 minutes and each minute has 60 seconds. APR stands for Annualised Percentage Rate.
Question 710 continuously compounding rate, continuously compounding rate conversion
A continuously compounded monthly return of 1% ##(r_\text{cc monthly})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
Question 711 continuously compounding rate, continuously compounding rate conversion
A continuously compounded semi-annual return of 5% ##(r_\text{cc 6mth})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
An effective monthly return of 1% ##(r_\text{eff monthly})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
An effective semi-annual return of 5% ##(r_\text{eff 6mth})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
Question 691 continuously compounding rate, effective rate, continuously compounding rate conversion, no explanation
A bank quotes an interest rate of 6% pa with quarterly compounding. Note that another way of stating this rate is that it is an annual percentage rate (APR) compounding discretely every 3 months.
Which of the following statements about this rate is NOT correct? All percentages are given to 6 decimal places. The equivalent:
Which of the following quantities is commonly assumed to be normally distributed?
If a variable, say X, is normally distributed with mean ##\mu## and variance ##\sigma^2## then mathematicians write ##X \sim \mathcal{N}(\mu, \sigma^2)##.
If a variable, say Y, is log-normally distributed and the underlying normal distribution has mean ##\mu## and variance ##\sigma^2## then mathematicians write ## Y \sim \mathbf{ln} \mathcal{N}(\mu, \sigma^2)##.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Select the most correct statement:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Which of the below statements is NOT correct?
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.

Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
The symbol ##\text{GDR}_{0\rightarrow 1}## represents a stock's gross discrete return per annum over the first year. ##\text{GDR}_{0\rightarrow 1} = P_1/P_0##. The subscript indicates the time period that the return is mentioned over. So for example, ##\text{AAGDR}_{1 \rightarrow 3}## is the arithmetic average GDR measured over the two year period from years 1 to 3, but it is expressed as a per annum rate.
Which of the below statements about the arithmetic and geometric average GDR is NOT correct?
Question 811 log-normal distribution, mean and median returns, return distribution, arithmetic and geometric averages
Which of the following statements about probability distributions is NOT correct?
Question 721 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some Commonwealth Bank (CBA) shares. He has calculated CBA’s monthly returns for each month in the past 20 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 1% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.01=1\% \text{ per month}###He also found the standard deviation of these monthly returns which was 5% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.05=5\%\text{ per month}###Which of the below statements about Fred’s CBA shares is NOT correct? Assume that the past historical average return is the true population average of future expected returns.
Question 722 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 50 | -0.6931 | 0.5 | -0.5 |
| 2 | 100 | 0.6931 | 2 | 1 |
| Arithmetic average | 0 | 1.25 | 0.25 | |
| Arithmetic standard deviation | 0.9802 | 1.0607 | 1.0607 | |
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 720 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed.
In 5 years, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 723 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 99 | -0.010050 | 0.990000 | -0.010000 |
| 2 | 180.40 | 0.600057 | 1.822222 | 0.822222 |
| 3 | 112.73 | 0.470181 | 0.624889 | 0.375111 |
| Arithmetic average | 0.0399 | 1.1457 | 0.1457 | |
| Arithmetic standard deviation | 0.4384 | 0.5011 | 0.5011 | |
Question 779 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some BHP shares. He has calculated BHP’s monthly returns for each month in the past 30 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 0.8% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.008=0.8\% \text{ per month}###He also found the standard deviation of these monthly returns which was 15% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.15=15\%\text{ per month}###Assume that the past historical average return is the true population average of future expected returns and the stock's returns calculated above ##(r_\text{t monthly})## are normally distributed. Which of the below statements about Fred’s BHP shares is NOT correct?
Question 792 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, log-normal distribution, confidence interval
A risk manager has identified that their investment fund’s continuously compounded portfolio returns are normally distributed with a mean of 10% pa and a standard deviation of 40% pa. The fund’s portfolio is currently valued at $1 million. Assume that there is no estimation error in the above figures. To simplify your calculations, all answers below use 2.33 as an approximation for the normal inverse cumulative density function at 99%. All answers are rounded to the nearest dollar. Assume one month is 1/12 of a year. Which of the following statements is NOT correct?
Question 877 arithmetic and geometric averages, utility, utility function
Gross discrete returns in different states of the world are presented in the table below. A gross discrete return is defined as ##P_1/P_0##, where ##P_0## is the price now and ##P_1## is the expected price in the future. An investor can purchase only a single asset, A, B, C or D. Assume that a portfolio of assets is not possible.
| Gross Discrete Returns | ||
| In Different States of the World | ||
| Investment | World states (probability) | |
| asset | Good (50%) | Bad (50%) |
| A | 2 | 0.5 |
| B | 1.1 | 0.9 |
| C | 1.1 | 0.95 |
| D | 1.01 | 1.01 |
Which of the following statements about the different assets is NOT correct? Asset:
Question 925 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate, no explanation
The arithmetic average and standard deviation of returns on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 were calculated as follows:
###\bar{r}_\text{yearly} = \dfrac{ \displaystyle\sum\limits_{t=1992}^{24}{\left( \ln \left( \dfrac{P_{t+1}}{P_t} \right) \right)} }{T} = \text{AALGDR} =0.0949=9.49\% \text{ pa}###
###\sigma_\text{yearly} = \dfrac{ \displaystyle\sum\limits_{t=1992}^{24}{\left( \left( \ln \left( \dfrac{P_{t+1}}{P_t} \right) - \bar{r}_\text{yearly} \right)^2 \right)} }{T} = \text{SDLGDR} = 0.1692=16.92\text{ pp pa}###
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
Which of the following statements is NOT correct? If you invested $1m today in the ASX200, then over the next 4 years:
Question 926 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the median dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Question 927 mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the mean dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Question 928 mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate, no explanation
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the mode dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Note that the mode of a log-normally distributed future price is: ##P_{T \text{ mode}} = P_0.e^{(\text{AALGDR} - \text{SDLGDR}^2 ).T} ##
Question 929 standard error, mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the data are sample statistics, not population statistics. Assume that the log gross discrete returns are normally distributed.
What is the standard error of your estimate of the sample ASX200 accumulation index arithmetic average log gross discrete return (AALGDR) over the 24 years from 1992 to 2016?
Which of the following statements about vanilla floating coupon bonds is NOT correct? A vanilla floating coupon bond's:
Which of the following statements about vanilla floating coupon bonds paying quarterly coupons is NOT correct? A vanilla floating coupon bond's:
Which of the below statements about utility is NOT generally accepted by economists? Most people are thought to:
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
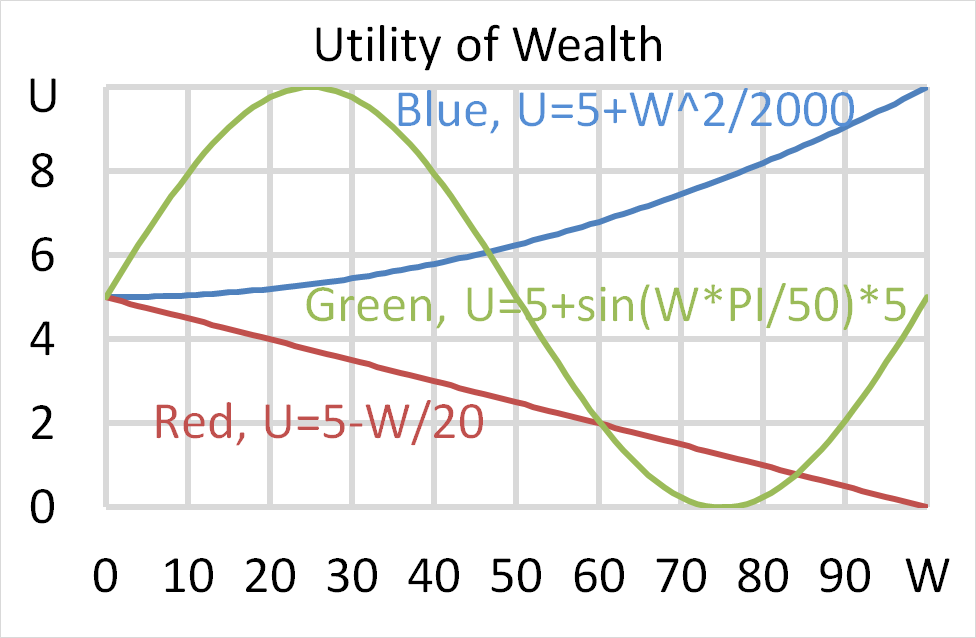
Question 699 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 700 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 701 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 702 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 703 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $500 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $500. Each player can flip a coin and if they flip heads, they receive $500. If they flip tails then they will lose $500. Which of the following statements is NOT correct?
Question 704 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $256 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $256. Each player can flip a coin and if they flip heads, they receive $256. If they flip tails then they will lose $256. Which of the following statements is NOT correct?

Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Note that a fair gamble is a bet that has an expected value of zero, such as paying $0.50 to win $1 in a coin flip with heads or nothing if it lands tails. Fairly priced insurance is when the expected present value of the insurance premiums is equal to the expected loss from the disaster that the insurance protects against, such as the cost of rebuilding a home after a catastrophic fire.
Which of the following statements is NOT correct?

Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Which of the following statements is NOT correct?
Below is a graph of 3 peoples’ utility functions, Mr Blue (U=W^(1/2) ), Miss Red (U=W/10) and Mrs Green (U=W^2/1000). Assume that each of them currently have $50 of wealth.

Which of the following statements about them is NOT correct?
(a) Mr Blue would prefer to invest his wealth in a well diversified portfolio of stocks rather than a single stock, assuming that all stocks had the same total risk and return.
Question 793 option, hedging, delta hedging, gamma hedging, gamma, Black-Scholes-Merton option pricing
A bank buys 1000 European put options on a $10 non-dividend paying stock at a strike of $12. The bank wishes to hedge this exposure. The bank can trade the underlying stocks and European call options with a strike price of 7 on the same stock with the same maturity. Details of the call and put options are given in the table below. Each call and put option is on a single stock.
| European Options on a Non-dividend Paying Stock | |||
| Description | Symbol | Put Values | Call Values |
| Spot price ($) | ##S_0## | 10 | 10 |
| Strike price ($) | ##K_T## | 12 | 7 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.4 | 0.4 |
| Option maturity (years) | ##T## | 1 | 1 |
| Option price ($) | ##p_0## or ##c_0## | 2.495350486 | 3.601466138 |
| ##N[d_1]## | ##\partial c/\partial S## | 0.888138405 | |
| ##N[d_2]## | ##N[d_2]## | 0.792946442 | |
| ##-N[-d_1]## | ##\partial p/\partial S## | -0.552034778 | |
| ##N[-d_2]## | ##N[-d_2]## | 0.207053558 | |
| Gamma | ##\Gamma = \partial^2 c/\partial S^2## or ##\partial^2 p/\partial S^2## | 0.098885989 | 0.047577422 |
| Theta | ##\Theta = \partial c/\partial T## or ##\partial p/\partial T## | 0.348152078 | 0.672379961 |
Which of the following statements is NOT correct?
Question 386 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The risky corporate debt graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?
Question 433 Merton model of corporate debt, real option, option, no explanation
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.
What is the payoff to equity holders at maturity, assuming that they keep their shares until maturity?
Question 434 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.
What is the payoff to debt holders at maturity, assuming that they keep their debt until maturity?
Question 381 Merton model of corporate debt, option, real option
In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying risk free government bonds and:
Question 382 Merton model of corporate debt, real option, option
In the Merton model of corporate debt, buying a levered company's shares is equivalent to:
Question 383 Merton model of corporate debt, real option, option
In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying the company's assets and:
Question 1003 Black-Scholes-Merton option pricing, log-normal distribution, return distribution, hedge fund, risk, financial distress
A hedge fund issued zero coupon bonds with a combined $1 billion face value due to be paid in 3 years. The promised yield to maturity is currently 6% pa given as a continuously compounded return (or log gross discrete return, ##LGDR=\ln[P_T/P_0] \div T##).
The hedge fund owns stock assets worth $1.1 billion now which are expected to have a 10% pa arithmetic average log gross discrete return ##(\text{AALGDR} = \sum\limits_{t=1}^T{\left( \ln[P_t/P_{t-1}] \right)} \div T)## and 30pp pa standard deviation (SDLGDR) in the future.
Analyse the hedge fund using the Merton model of corporate equity as an option on the firm's assets.
The risk free government bond yield to maturity is currently 5% pa given as a continuously compounded return or LGDR.
Which of the below statements is NOT correct? All figures are rounded to the sixth decimal place.
Being long a call and short a put which have the same exercise prices and underlying stock is equivalent to being:
A stock, a call, a put and a bond are available to trade. The call and put options' underlying asset is the stock they and have the same strike prices, ##K_T##.
Being long the call and short the stock is equivalent to being:
A stock, a call, a put and a bond are available to trade. The call and put options' underlying asset is the stock they and have the same strike prices, ##K_T##.
You are currently long the stock. You want to hedge your long stock position without actually trading the stock. How would you do this?
A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the put option?