The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
What is the Internal Rate of Return (IRR) of the project detailed in the table below?
Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
The below graph shows a project's net present value (NPV) against its annual discount rate.
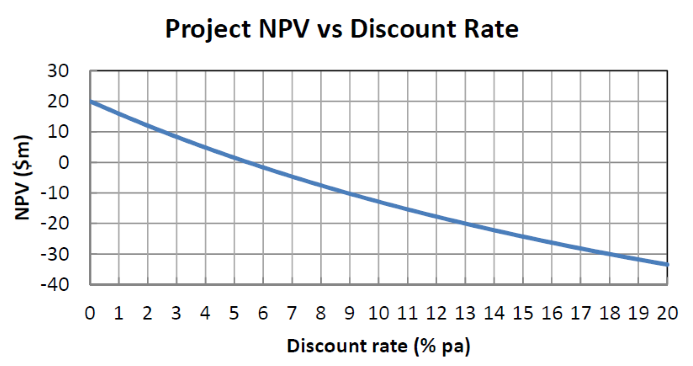
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
The below graph shows a project's net present value (NPV) against its annual discount rate.

Which of the following statements is NOT correct?
The saying "buy low, sell high" suggests that investors should make a:
Total cash flows can be broken into income and capital cash flows. What is the name given to the income cash flow from owning shares?
An asset's total expected return over the next year is given by:
###r_\text{total} = \dfrac{c_1+p_1-p_0}{p_0} ###
Where ##p_0## is the current price, ##c_1## is the expected income in one year and ##p_1## is the expected price in one year. The total return can be split into the income return and the capital return.
Which of the following is the expected capital return?
Question 542 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to double every 10 years, what must be the expected future capital return, given as an effective annual rate?
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 993 inflation, real and nominal returns and cash flows
In February 2020, the RBA cash rate was 0.75% pa and the Australian CPI inflation rate was 1.8% pa.
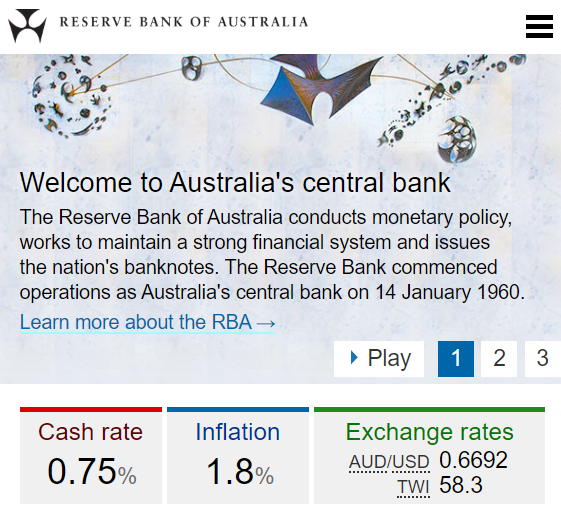
You currently have $100 in the bank which pays a 0.75% pa interest rate.
Apples currently cost $1 each at the shop and inflation is 1.8% pa which is the expected growth rate in the apple price.
This information is summarised in the table below, with some parts missing that correspond to the answer options. All rates are given as effective annual rates. Note that when payments are not specified as real, as in this question, they're conventionally assumed to be nominal.
| Wealth in Dollars and Apples | ||||
| Time (year) | Bank account wealth ($) | Apple price ($) | Wealth in apples | |
| 0 | 100 | 1 | 100 | |
| 1 | 100.75 | 1.018 | (a) | |
| 2 | (b) | (c) | (d) | |
Which of the following statements is NOT correct? Your:
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 407 income and capital returns, inflation, real and nominal returns and cash flows
A stock has a real expected total return of 7% pa and a real expected capital return of 2% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What is the nominal expected total return, capital return and dividend yield? The answers below are given in the same order.
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 577 inflation, real and nominal returns and cash flows
What is the present value of a real payment of $500 in 2 years? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Question 554 inflation, real and nominal returns and cash flows
On his 20th birthday, a man makes a resolution. He will put $30 cash under his bed at the end of every month starting from today. His birthday today is the first day of the month. So the first addition to his cash stash will be in one month. He will write in his will that when he dies the cash under the bed should be given to charity.
If the man lives for another 60 years, how much money will be under his bed if he dies just after making his last (720th) addition?
Also, what will be the real value of that cash in today's prices if inflation is expected to 2.5% pa? Assume that the inflation rate is an effective annual rate and is not expected to change.
The answers are given in the same order, the amount of money under his bed in 60 years, and the real value of that money in today's prices.
Question 745 real and nominal returns and cash flows, inflation, income and capital returns
If the nominal gold price is expected to increase at the same rate as inflation which is 3% pa, which of the following statements is NOT correct?
Which business structure or structures have the advantage of limited liability for equity investors?
Which of the following statements about book and market equity is NOT correct?
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.
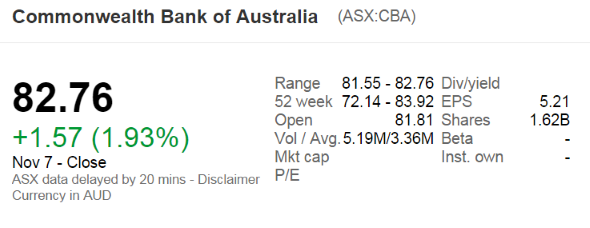
What was CBA's market capitalisation of equity?
Question 443 corporate financial decision theory, investment decision, financing decision, working capital decision, payout policy
Business people make lots of important decisions. Which of the following is the most important long term decision?
Katya offers to pay you $10 at the end of every year for the next 5 years (t=1,2,3,4,5) if you pay her $50 now (t=0). You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate. Ignore credit risk.
This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
A stock is expected to pay its next dividend of $1 in one year. Future annual dividends are expected to grow by 2% pa. So the first dividend of $1 will be in one year, the year after that $1.02 (=1*(1+0.02)^1), and a year later $1.0404 (=1*(1+0.02)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
A stock just paid a dividend of $1. Future annual dividends are expected to grow by 2% pa. The next dividend of $1.02 (=1*(1+0.02)^1) will be in one year, and the year after that the dividend will be $1.0404 (=1*(1+0.02)^2), and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
For a price of $13, Carla will sell you a share paying a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.
For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.
The required return of the stock is 15% pa.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
The following is the Dividend Discount Model (DDM) used to price stocks:
###P_0=\dfrac{C_1}{r-g}###
If the assumptions of the DDM hold and the stock is fairly priced, which one of the following statements is NOT correct? The long term expected:
Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
In the dividend discount model:
###P_0 = \dfrac{C_1}{r-g}###
The return ##r## is supposed to be the:
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_0 = \frac{d_1}{r - g} ###
Which expression is NOT equal to the expected dividend yield?
A fairly valued share's current price is $4 and it has a total required return of 30%. Dividends are paid annually and next year's dividend is expected to be $1. After that, dividends are expected to grow by 5% pa in perpetuity. All rates are effective annual returns.
What is the expected dividend income paid at the end of the second year (t=2) and what is the expected capital gain from just after the first dividend (t=1) to just after the second dividend (t=2)? The answers are given in the same order, the dividend and then the capital gain.
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
A home loan company advertises an interest rate of 6% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A semi-annual coupon bond has a yield of 3% pa. Which of the following statements about the yield is NOT correct? All rates are given to four decimal places.
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
Question 579 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to double if the price grows by 10% pa?
Question 580 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to quadruple (be four times as big, say from $1 to $4) if the price grows by 15% pa?
A young lady is trying to decide if she should attend university or not.
The young lady's parents say that she must attend university because otherwise all of her hard work studying and attending school during her childhood was a waste.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The hard work studying at school in her childhood should be classified as:
Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
Over the next year, the management of an unlevered company plans to:
- Achieve firm free cash flow (FFCF or CFFA) of $1m.
- Pay dividends of $1.8m
- Complete a $1.3m share buy-back.
- Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Find the cash flow from assets (CFFA) of the following project.
| Project Data | ||
| Project life | 2 years | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year for tax purposes | $1m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $3 | |
| Fixed costs per year, paid at the end of each year | $1.5m | |
| Tax rate | 30% | |
Note 1: The equipment will have a book value of $4m at the end of the project for tax purposes. However, the equipment is expected to fetch $0.9 million when it is sold at t=2.
Note 2: Due to the project, the firm will have to purchase $0.8m of inventory initially, which it will sell at t=1. The firm will buy another $0.8m at t=1 and sell it all again at t=2 with zero inventory left. The project will have no effect on the firm's current liabilities.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
A credit card company advertises an interest rate of 18% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which of the following equations is NOT equal to the total return of an asset?
Let ##p_0## be the current price, ##p_1## the expected price in one year and ##c_1## the expected income in one year.
A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).
What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
In the 'Austin Powers' series of movies, the character Dr. Evil threatens to destroy the world unless the United Nations pays him a ransom (video 1, video 2). Dr. Evil makes the threat on two separate occasions:
- In 1969 he demands a ransom of $1 million (=10^6), and again;
- In 1997 he demands a ransom of $100 billion (=10^11).
If Dr. Evil's demands are equivalent in real terms, in other words $1 million will buy the same basket of goods in 1969 as $100 billion would in 1997, what was the implied inflation rate over the 28 years from 1969 to 1997?
The answer choices below are given as effective annual rates:
Question 363 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 8% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.
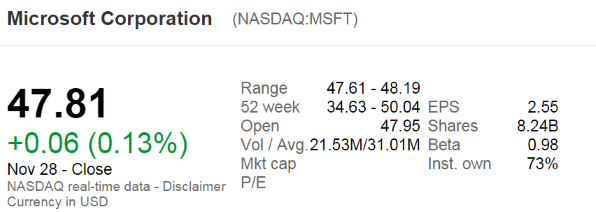
What was MSFT's market capitalisation of equity?
Question 461 book and market values, ROE, ROA, market efficiency
One year ago a pharmaceutical firm floated by selling its 1 million shares for $100 each. Its book and market values of equity were both $100m. Its debt totalled $50m. The required return on the firm's assets was 15%, equity 20% and debt 5% pa.
In the year since then, the firm:
- Earned net income of $29m.
- Paid dividends totaling $10m.
- Discovered a valuable new drug that will lead to a massive 1,000 times increase in the firm's net income in 10 years after the research is commercialised. News of the discovery was publicly announced. The firm's systematic risk remains unchanged.
Which of the following statements is NOT correct? All statements are about current figures, not figures one year ago.
Hint: Book return on assets (ROA) and book return on equity (ROE) are ratios that accountants like to use to measure a business's past performance.
###\text{ROA}= \dfrac{\text{Net income}}{\text{Book value of assets}}###
###\text{ROE}= \dfrac{\text{Net income}}{\text{Book value of equity}}###
The required return on assets ##r_V## is a return that financiers like to use to estimate a business's future required performance which compensates them for the firm's assets' risks. If the business were to achieve realised historical returns equal to its required returns, then investment into the business's assets would have been a zero-NPV decision, which is neither good nor bad but fair.
###r_\text{V, 0 to 1}= \dfrac{\text{Cash flow from assets}_\text{1}}{\text{Market value of assets}_\text{0}} = \dfrac{CFFA_\text{1}}{V_\text{0}}###
Similarly for equity and debt.
Question 446 working capital decision, corporate financial decision theory
The working capital decision primarily affects which part of a business?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
Question 452 limited liability, expected and historical returns
What is the lowest and highest expected share price and expected return from owning shares in a company over a finite period of time?
Let the current share price be ##p_0##, the expected future share price be ##p_1##, the expected future dividend be ##d_1## and the expected return be ##r##. Define the expected return as:
##r=\dfrac{p_1-p_0+d_1}{p_0} ##
The answer choices are stated using inequalities. As an example, the first answer choice "(a) ##0≤p<∞## and ##0≤r< 1##", states that the share price must be larger than or equal to zero and less than positive infinity, and that the return must be larger than or equal to zero and less than one.
There are many ways to write the ordinary annuity formula.
Which of the following is NOT equal to the ordinary annuity formula?
The following cash flows are expected:
- 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
- 1 payment of $400 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
The first payment of a constant perpetual annual cash flow is received at time 5. Let this cash flow be ##C_5## and the required return be ##r##.
So there will be equal annual cash flows at time 5, 6, 7 and so on forever, and all of the cash flows will be equal so ##C_5 = C_6 = C_7 = ...##
When the perpetuity formula is used to value this stream of cash flows, it will give a value (V) at time:
A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.
What is the implied growth rate of the dividend per year?
A stock is expected to pay a dividend of $15 in one year (t=1), then $25 for 9 years after that (payments at t=2 ,3,...10), and on the 11th year (t=11) the dividend will be 2% less than at t=10, and will continue to shrink at the same rate every year after that forever. The required return of the stock is 10%. All rates are effective annual rates.
What is the price of the stock now?
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.
What is the price of the share now?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.
Using the dividend discount model, what will be the share price?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which firms tend to have high forward-looking price-earnings (PE) ratios?
Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
A low-quality second-hand car can be bought now for $1,000 and will last for 1 year before it will be scrapped for nothing.
A high-quality second-hand car can be bought now for $4,900 and it will last for 5 years before it will be scrapped for nothing.
What is the equivalent annual cost of each car? Assume a discount rate of 10% pa, given as an effective annual rate.
The answer choices are given as the equivalent annual cost of the low-quality car and then the high quality car.
You're advising your superstar client 40-cent who is weighing up buying a private jet or a luxury yacht. 40-cent is just as happy with either, but he wants to go with the more cost-effective option. These are the cash flows of the two options:
- The private jet can be bought for $6m now, which will cost $12,000 per month in fuel, piloting and airport costs, payable at the end of each month. The jet will last for 12 years.
- Or the luxury yacht can be bought for $4m now, which will cost $20,000 per month in fuel, crew and berthing costs, payable at the end of each month. The yacht will last for 20 years.
What's unusual about 40-cent is that he is so famous that he will actually be able to sell his jet or yacht for the same price as it was bought since the next generation of superstar musicians will buy it from him as a status symbol.
Bank interest rates are 10% pa, given as an effective annual rate. You can assume that 40-cent will live for another 60 years and that when the jet or yacht's life is at an end, he will buy a new one with the same details as above.
Would you advise 40-cent to buy the or the ?
Note that the effective monthly rate is ##r_\text{eff monthly}=(1+0.1)^{1/12}-1=0.00797414##
An industrial chicken farmer grows chickens for their meat. Chickens:
- Cost $0.50 each to buy as chicks. They are bought on the day they’re born, at t=0.
- Grow at a rate of $0.70 worth of meat per chicken per week for the first 6 weeks (t=0 to t=6).
- Grow at a rate of $0.40 worth of meat per chicken per week for the next 4 weeks (t=6 to t=10) since they’re older and grow more slowly.
- Feed costs are $0.30 per chicken per week for their whole life. Chicken feed is bought and fed to the chickens once per week at the beginning of the week. So the first amount of feed bought for a chicken at t=0 costs $0.30, and so on.
- Can be slaughtered (killed for their meat) and sold at no cost at the end of the week. The price received for the chicken is their total value of meat (note that the chicken grows fast then slow, see above).
The required return of the chicken farm is 0.5% given as an effective weekly rate.
Ignore taxes and the fixed costs of the factory. Ignore the chicken’s welfare and other environmental and ethical concerns.
Find the equivalent weekly cash flow of slaughtering a chicken at 6 weeks and at 10 weeks so the farmer can figure out the best time to slaughter his chickens. The choices below are given in the same order, 6 and 10 weeks.
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
Which of the following statements is NOT equivalent to the yield on debt?
Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
In Australia in the 1980's, inflation was around 8% pa, and residential mortgage loan interest rates were around 14%.
In 2013, inflation was around 2.5% pa, and residential mortgage loan interest rates were around 4.5%.
If a person can afford constant mortgage loan payments of $2,000 per month, how much more can they borrow when interest rates are 4.5% pa compared with 14.0% pa?
Give your answer as a proportional increase over the amount you could borrow when interest rates were high ##(V_\text{high rates})##, so:
###\text{Proportional increase} = \dfrac{V_\text{low rates}-V_\text{high rates}}{V_\text{high rates}} ###
Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates (APR's) compounding per month.
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
Question 48 IRR, NPV, bond pricing, premium par and discount bonds, market efficiency
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
Question 56 income and capital returns, bond pricing, premium par and discount bonds
Which of the following statements about risk free government bonds is NOT correct?
Hint: Total return can be broken into income and capital returns as follows:
###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###
The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
Bonds A and B are issued by the same Australian company. Both bonds yield 7% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond A pays coupons of 10% pa and bond B pays coupons of 5% pa. Which of the following statements is true about the bonds' prices?
Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100) and maturity (3 years).
The only difference is that bond X and Y's yields are 8 and 12% pa respectively. Which of the following statements is true?
Which one of the following bonds is trading at a discount?
A firm wishes to raise $20 million now. They will issue 8% pa semi-annual coupon bonds that will mature in 5 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
Which one of the following bonds is trading at par?
In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.
A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?
A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.
Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?
Below are some statements about loans and bonds. The first descriptive sentence is correct. But one of the second sentences about the loans' or bonds' prices is not correct. Which statement is NOT correct? Assume that interest rates are positive.
Note that coupons or interest payments are the periodic payments made throughout a bond or loan's life. The face or par value of a bond or loan is the amount paid at the end when the debt matures.
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 8 years and have a face value of $1,000 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue? All numbers are rounded up.
Bonds X and Y are issued by the same US company. Both bonds yield 6% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X pays coupons of 8% pa and bond Y pays coupons of 12% pa. Which of the following statements is true?
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Find Ching-A-Lings Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Ching-A-Lings Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 20 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 30 | |
| Taxes at 30% | 9 | |
| Net income | 21 | |
| Ching-A-Lings Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 49 | 38 |
| Trade debtors | 14 | 2 |
| Rent paid in advance | 5 | 5 |
| PPE | 400 | 400 |
| Total assets | 468 | 445 |
| Trade creditors | 4 | 10 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 145 | 145 |
| Retained profits | 119 | 100 |
| Total L and OE | 468 | 445 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Read the following financial statements and calculate the firm's free cash flow over the 2014 financial year.
| UBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2014 | ||
| $m | ||
| Sales | 293 | |
| COGS | 200 | |
| Rent expense | 15 | |
| Gas expense | 8 | |
| Depreciation | 10 | |
| EBIT | 60 | |
| Interest expense | 0 | |
| Taxable income | 60 | |
| Taxes | 18 | |
| Net income | 42 | |
| UBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2014 | 2013 |
| $m | $m | |
| Assets | ||
| Cash | 30 | 29 |
| Accounts receivable | 5 | 7 |
| Pre-paid rent expense | 1 | 0 |
| Inventory | 50 | 46 |
| PPE | 290 | 300 |
| Total assets | 376 | 382 |
| Liabilities | ||
| Trade payables | 20 | 18 |
| Accrued gas expense | 3 | 2 |
| Non-current liabilities | 0 | 0 |
| Contributed equity | 212 | 212 |
| Retained profits | 136 | 150 |
| Asset revaluation reserve | 5 | 0 |
| Total L and OE | 376 | 382 |
Note: all figures are given in millions of dollars ($m).
The firm's free cash flow over the 2014 financial year was:
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
Many Australian home loans that are interest-only actually require payments to be made on a fully amortising basis after a number of years.
You decide to borrow $600,000 from the bank at an interest rate of 4.25% pa for 25 years. The payments will be interest-only for the first 10 years (t=0 to 10 years), then they will have to be paid on a fully amortising basis for the last 15 years (t=10 to 25 years).
Assuming that interest rates will remain constant, what will be your monthly payments over the first 10 years from now, and then the next 15 years after that? The answer options are given in the same order.
A young lady is trying to decide if she should attend university. Her friends say that she should go to university because she is more likely to meet a clever young man than if she begins full time work straight away.
What's the correct way to classify this item from a capital budgeting perspective when trying to find the Net Present Value of going to university rather than working?
The opportunity to meet a desirable future spouse should be classified as:
A man is thinking about taking a day off from his casual painting job to relax.
He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.
But he's thinking about the hours that he could work today (in the future) which are:
A man has taken a day off from his casual painting job to relax.
It's the end of the day and he's thinking about the hours that he could have spent working (in the past) which are now:
Find the cash flow from assets (CFFA) of the following project.
| One Year Mining Project Data | ||
| Project life | 1 year | |
| Initial investment in building mine and equipment | $9m | |
| Depreciation of mine and equipment over the year | $8m | |
| Kilograms of gold mined at end of year | 1,000 | |
| Sale price per kilogram | $0.05m | |
| Variable cost per kilogram | $0.03m | |
| Before-tax cost of closing mine at end of year | $4m | |
| Tax rate | 30% | |
Note 1: Due to the project, the firm also anticipates finding some rare diamonds which will give before-tax revenues of $1m at the end of the year.
Note 2: The land that will be mined actually has thermal springs and a family of koalas that could be sold to an eco-tourist resort for an after-tax amount of $3m right now. However, if the mine goes ahead then this natural beauty will be destroyed.
Note 3: The mining equipment will have a book value of $1m at the end of the year for tax purposes. However, the equipment is expected to fetch $2.5m when it is sold.
Find the project's CFFA at time zero and one. Answers are given in millions of dollars ($m), with the first cash flow at time zero, and the second at time one.
The hardest and most important aspect of business project valuation is the estimation of the:
Find the cash flow from assets (CFFA) of the following project.
| Project Data | |
| Project life | 2 years |
| Initial investment in equipment | $8m |
| Depreciation of equipment per year for tax purposes | $3m |
| Unit sales per year | 10m |
| Sale price per unit | $9 |
| Variable cost per unit | $4 |
| Fixed costs per year, paid at the end of each year | $2m |
| Tax rate | 30% |
Note 1: Due to the project, the firm will have to purchase $40m of inventory initially (at t=0). Half of this inventory will be sold at t=1 and the other half at t=2.
Note 2: The equipment will have a book value of $2m at the end of the project for tax purposes. However, the equipment is expected to fetch $1m when it is sold. Assume that the full capital loss is tax-deductible and taxed at the full corporate tax rate.
Note 3: The project will be fully funded by equity which investors will expect to pay dividends totaling $10m at the end of each year.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the balance sheet needed? Note that the balance sheet is sometimes also called the statement of financial position.
Question 658 CFFA, income statement, balance sheet, no explanation
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the income statement needed? Note that the income statement is sometimes also called the profit and loss, P&L, or statement of financial performance.
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
A project's NPV is positive. Select the most correct statement:
Question 543 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to triple every 5 years, what must be the expected future capital return, given as an effective annual rate?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume half as much now (t=0) as in one year (t=1) and have nothing left in the bank at the end.
How much can you consume at time zero and one? The answer choices are given in the same order.
A project to build a toll road will take 3 years to complete, costing three payments of $50 million, paid at the start of each year (at times 0, 1, and 2).
After completion, the toll road will yield a constant $10 million at the end of each year forever with no costs. So the first payment will be at t=4.
The required return of the project is 10% pa given as an effective nominal rate. All cash flows are nominal.
What is the payback period?
A firm is considering a business project which costs $10m now and is expected to pay a single cash flow of $12.1m in two years.
Assume that the initial $10m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
Question 524 risk, expected and historical returns, bankruptcy or insolvency, capital structure, corporate financial decision theory, limited liability
Which of the following statements is NOT correct?
Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| UniBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 80 | |
| COGS | 40 | |
| Operating expense | 15 | |
| Depreciation | 10 | |
| Interest expense | 5 | |
| Income before tax | 10 | |
| Tax at 30% | 3 | |
| Net income | 7 | |
| UniBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 90 |
| PPE | ||
| Cost | 360 | 320 |
| Accumul. depr. | 40 | 30 |
| Carrying amount | 320 | 290 |
| Total assets | 440 | 380 |
| Liabilities | ||
| Current liabilities | 110 | 60 |
| Non-current liabilities | 190 | 180 |
| Owners' equity | ||
| Retained earnings | 95 | 95 |
| Contributed equity | 45 | 45 |
| Total L and OE | 440 | 380 |
Note: all figures are given in millions of dollars ($m).
A firm has a debt-to-assets ratio of 20%. What is its debt-to-equity ratio?
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
Question 772 interest tax shield, capital structure, leverage
A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?
A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.
Ignoring the costs of financial distress, which of the following statements is NOT correct:
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use earnings before interest and tax (EBIT).
###\begin{aligned} FFCF &= (EBIT)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ \end{aligned} \\###
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of equity to raise money for new projects of similar systematic risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Question 418 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $8m | |
| Depreciation of equipment per year | $8m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 4m | |
| Sale price per unit | $10 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense in first year (at t=1) | $0.562m | |
| Corporate tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 9% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.32 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-equity ratio | 50% | |
Notes
- Due to the project, current assets will increase by $6m now (t=0) and fall by $6m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa. All rates are given as effective annual rates.
- The project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Question 803 capital raising, rights issue, initial public offering, on market repurchase, no explanation
Which one of the following capital raisings or payouts involve the sale of shares to existing shareholders only?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
Diversification in a portfolio of two assets works best when the correlation between their returns is:
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
All things remaining equal, the higher the correlation of returns between two stocks:
Question 556 portfolio risk, portfolio return, standard deviation
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 12% pa.
- Stock A has an expected return of 10% pa and a standard deviation of 20% pa.
- Stock B has an expected return of 15% pa and a standard deviation of 30% pa.
The correlation coefficient between stock A and B's expected returns is 70%.
What will be the annual standard deviation of the portfolio with this 12% pa target return?
Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
A fairly priced stock has an expected return equal to the market's. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the stock's beta?
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
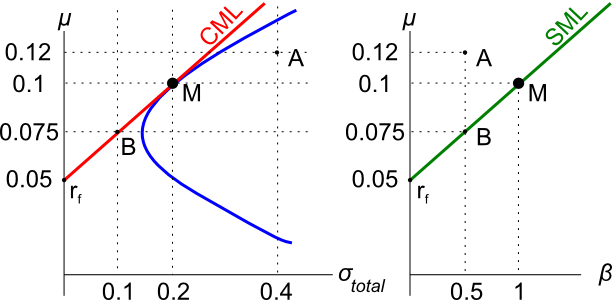
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?

Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
What do you think will be the stock's expected return over the next year, given as an effective annual rate?
A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
The CAPM can be used to find a business's expected opportunity cost of capital:
###r_i=r_f+β_i (r_m-r_f)###
What should be used as the risk free rate ##r_f##?
Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?
Fundamentalists who analyse company financial reports and news announcements (but who don't have inside information) will make positive abnormal returns if:
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Assume that there are no dividend payments so the entire 15% total return is all capital return.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% return lasts for the next 100 years (t=0 to 100), then reverts to 10% pa after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant. All returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
In 2014 the median starting salaries of male and female Australian bachelor degree accounting graduates aged less than 25 years in their first full-time industry job was $50,000 before tax, according to Graduate Careers Australia. See page 9 of this report. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below.
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $50,000 per annum before-tax?
Question 494 franking credit, personal tax on dividends, imputation tax system
A firm pays a fully franked cash dividend of $100 to one of its Australian shareholders who has a personal marginal tax rate of 15%. The corporate tax rate is 30%.
What will be the shareholder's personal tax payable due to the dividend payment?
Due to floods overseas, there is a cut in the supply of the mineral iron ore and its price increases dramatically. An Australian iron ore mining company therefore expects a large but temporary increase in its profit and cash flows. The mining company does not have any positive NPV projects to begin, so what should it do? Select the most correct answer.
A pharmaceutical firm has just discovered a valuable new drug. So far the news has been kept a secret.
The net present value of making and commercialising the drug is $200 million, but $600 million of bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and bond raising to shareholders simultaneously in the same announcement. The bonds will be issued shortly after.
Once the announcement is made and the bonds are issued, what is the expected increase in the value of the firm's assets (ΔV), market capitalisation of debt (ΔD) and market cap of equity (ΔE)?
The triangle symbol is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##ΔV = ΔD+ΔE##
Question 513 stock split, reverse stock split, stock dividend, bonus issue, rights issue
Which of the following statements is NOT correct?
Question 566 capital structure, capital raising, rights issue, on market repurchase, dividend, stock split, bonus issue
A company's share price fell by 20% and its number of shares rose by 25%. Assume that there are no taxes, no signalling effects and no transaction costs.
Which one of the following corporate events may have happened?
In mid 2009 the listed mining company Rio Tinto announced a 21-for-40 renounceable rights issue. Below is the chronology of events:
- 04/06/2009. Share price opens at $69.00 and closes at $66.90.
- 05/06/2009. 21-for-40 rights issue announced at a subscription price of $28.29.
- 16/06/2009. Last day that shares trade cum-rights. Share price opens at $76.40 and closes at $75.50.
- 17/06/2009. Shares trade ex-rights. Rights trading commences.
All things remaining equal, what would you expect Rio Tinto's stock price to open at on the first day that it trades ex-rights (17/6/2009)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
Question 708 continuously compounding rate, continuously compounding rate conversion
Convert a 10% continuously compounded annual rate ##(r_\text{cc annual})## into an effective annual rate ##(r_\text{eff annual})##. The equivalent effective annual rate is:
Question 710 continuously compounding rate, continuously compounding rate conversion
A continuously compounded monthly return of 1% ##(r_\text{cc monthly})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
An effective monthly return of 1% ##(r_\text{eff monthly})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
Which of the following quantities is commonly assumed to be normally distributed?
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Which of the below statements is NOT correct?
The symbol ##\text{GDR}_{0\rightarrow 1}## represents a stock's gross discrete return per annum over the first year. ##\text{GDR}_{0\rightarrow 1} = P_1/P_0##. The subscript indicates the time period that the return is mentioned over. So for example, ##\text{AAGDR}_{1 \rightarrow 3}## is the arithmetic average GDR measured over the two year period from years 1 to 3, but it is expressed as a per annum rate.
Which of the below statements about the arithmetic and geometric average GDR is NOT correct?
Question 811 log-normal distribution, mean and median returns, return distribution, arithmetic and geometric averages
Which of the following statements about probability distributions is NOT correct?
Question 721 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some Commonwealth Bank (CBA) shares. He has calculated CBA’s monthly returns for each month in the past 20 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 1% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.01=1\% \text{ per month}###He also found the standard deviation of these monthly returns which was 5% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.05=5\%\text{ per month}###Which of the below statements about Fred’s CBA shares is NOT correct? Assume that the past historical average return is the true population average of future expected returns.
When someone says that they're "buying American dollars" (USD), what type of asset are they probably buying? They're probably buying:
An Indonesian lady wishes to convert 1 million Indonesian rupiah (IDR) to Australian dollars (AUD). Exchange rates are 13,125 IDR per USD and 0.79 USD per AUD. How many AUD is the IDR 1 million worth?
Question 315 foreign exchange rate, American and European terms
If the current AUD exchange rate is USD 0.9686 = AUD 1, what is the European terms quote of the AUD against the USD?
Question 319 foreign exchange rate, monetary policy, American and European terms
Investors expect the Reserve Bank of Australia (RBA) to keep the policy rate steady at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 25 basis points due to fears that the economy is growing too fast and that inflation will be above their target rate of 2 to 3 per cent.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:
Question 321 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 50 basis points due to high future GDP and inflation forecasts.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar will:
Question 626 cross currency interest rate parity, foreign exchange rate, forward foreign exchange rate
The Australian cash rate is expected to be 2% pa over the next one year, while the Japanese cash rate is expected to be 0% pa, both given as nominal effective annual rates. The current exchange rate is 100 JPY per AUD.
What is the implied 1 year forward foreign exchange rate?
Question 246 foreign exchange rate, forward foreign exchange rate, cross currency interest rate parity
Suppose the Australian cash rate is expected to be 8.15% pa and the US federal funds rate is expected to be 3.00% pa over the next 2 years, both given as nominal effective annual rates. The current exchange rate is at parity, so 1 USD = 1 AUD.
What is the implied 2 year forward foreign exchange rate?
The Chinese government attempts to fix its exchange rate against the US dollar and at the same time use monetary policy to fix its interest rate at a set level.
To be able to fix its exchange rate and interest rate in this way, what does the Chinese government actually do?
- Adopts capital controls to prevent financial arbitrage by private firms and individuals.
- Adopts the same interest rate (monetary policy) as the United States.
- Fixes inflation so that the domestic real interest rate is equal to the United States' real interest rate.
Which of the above statements is or are true?
Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Piano Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 310 | |
| COGS | 185 | |
| Operating expense | 20 | |
| Depreciation | 15 | |
| Interest expense | 10 | |
| Income before tax | 80 | |
| Tax at 30% | 24 | |
| Net income | 56 | |
| Piano Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 240 | 230 |
| PPE | ||
| Cost | 420 | 400 |
| Accumul. depr. | 50 | 35 |
| Carrying amount | 370 | 365 |
| Total assets | 610 | 595 |
| Liabilities | ||
| Current liabilities | 180 | 190 |
| Non-current liabilities | 290 | 265 |
| Owners' equity | ||
| Retained earnings | 90 | 90 |
| Contributed equity | 50 | 50 |
| Total L and OE | 610 | 595 |
Note: all figures are given in millions of dollars ($m).
Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| World Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 300 | |
| COGS | 150 | |
| Operating expense | 50 | |
| Depreciation | 40 | |
| Interest expense | 10 | |
| Taxable income | 50 | |
| Tax at 30% | 15 | |
| Net income | 35 | |
| World Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 200 | 230 |
| PPE | ||
| Cost | 400 | 400 |
| Accumul. depr. | 75 | 35 |
| Carrying amount | 325 | 365 |
| Total assets | 525 | 595 |
| Liabilities | ||
| Current liabilities | 150 | 205 |
| Non-current liabilities | 235 | 250 |
| Owners' equity | ||
| Retained earnings | 100 | 100 |
| Contributed equity | 40 | 40 |
| Total L and OE | 525 | 595 |
Note: all figures above and below are given in millions of dollars ($m).
Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Scubar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 60 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 90 | |
| Taxes at 30% | 27 | |
| Net income | 63 | |
| Scubar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 60 | 50 |
| Trade debtors | 19 | 6 |
| Rent paid in advance | 3 | 2 |
| PPE | 420 | 400 |
| Total assets | 502 | 458 |
| Trade creditors | 10 | 8 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 130 | 130 |
| Retained profits | 162 | 130 |
| Total L and OE | 502 | 458 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
You own some nice shoes which you use once per week on date nights. You bought them 2 years ago for $500. In your experience, shoes used once per week last for 6 years. So you expect yours to last for another 4 years.
Your younger sister said that she wants to borrow your shoes once per week. With the increased use, your shoes will only last for another 2 years rather than 4.
What is the present value of the cost of letting your sister use your current shoes for the next 2 years?
Assume: that bank interest rates are 10% pa, given as an effective annual rate; you will buy a new pair of shoes when your current pair wears out and your sister will not use the new ones; your sister will only use your current shoes so she will only use it for the next 2 years; and the price of new shoes never changes.
A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?
A firm wishes to raise $8 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Question 413 CFFA, interest tax shield, depreciation tax shield
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA).
One method is to use the following formulas to transform net income (NI) into FFCF including interest and depreciation tax shields:
###FFCF=NI + Depr - CapEx -ΔNWC + IntExp###
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )###
Another popular method is to use EBITDA rather than net income. EBITDA is defined as:
###EBITDA=Rev - COGS - FC###
One of the below formulas correctly calculates FFCF from EBITDA, including interest and depreciation tax shields, giving an identical answer to that above. Which formula is correct?
Select the most correct statement from the following.
'Chartists', also known as 'technical traders', believe that:
Question 100 market efficiency, technical analysis, joint hypothesis problem
A company selling charting and technical analysis software claims that independent academic studies have shown that its software makes significantly positive abnormal returns. Assuming the claim is true, which statement(s) are correct?
(I) Weak form market efficiency is broken.
(II) Semi-strong form market efficiency is broken.
(III) Strong form market efficiency is broken.
(IV) The asset pricing model used to measure the abnormal returns (such as the CAPM) had mis-specification error so the returns may not be abnormal but rather fair for the level of risk.
Select the most correct response:
Question 707 continuously compounding rate, continuously compounding rate conversion
Convert a 10% effective annual rate ##(r_\text{eff annual})## into a continuously compounded annual rate ##(r_\text{cc annual})##. The equivalent continuously compounded annual rate is:
Question 711 continuously compounding rate, continuously compounding rate conversion
A continuously compounded semi-annual return of 5% ##(r_\text{cc 6mth})## is equivalent to a continuously compounded annual return ##(r_\text{cc annual})## of:
An effective semi-annual return of 5% ##(r_\text{eff 6mth})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
Question 691 continuously compounding rate, effective rate, continuously compounding rate conversion, no explanation
A bank quotes an interest rate of 6% pa with quarterly compounding. Note that another way of stating this rate is that it is an annual percentage rate (APR) compounding discretely every 3 months.
Which of the following statements about this rate is NOT correct? All percentages are given to 6 decimal places. The equivalent:
If a variable, say X, is normally distributed with mean ##\mu## and variance ##\sigma^2## then mathematicians write ##X \sim \mathcal{N}(\mu, \sigma^2)##.
If a variable, say Y, is log-normally distributed and the underlying normal distribution has mean ##\mu## and variance ##\sigma^2## then mathematicians write ## Y \sim \mathbf{ln} \mathcal{N}(\mu, \sigma^2)##.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Select the most correct statement:
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.

Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.