A company runs a number of slaughterhouses which supply hamburger meat to McDonalds. The company is afraid that live cattle prices will increase over the next year, even though there is widespread belief in the market that they will be stable. What can the company do to hedge against the risk of increasing live cattle prices? Which statement(s) are correct?
(i) buy call options on live cattle.
(ii) buy put options on live cattle.
(iii) sell call options on live cattle.
Select the most correct response:
Below are 4 option graphs. Note that the y-axis is payoff at maturity (T). What options do they depict? List them in the order that they are numbered.
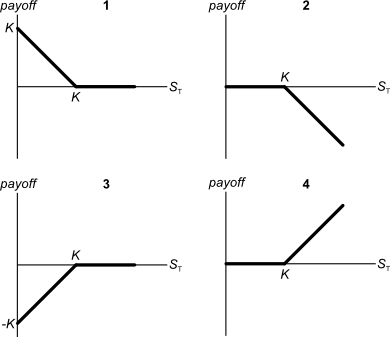
You have just sold an 'in the money' 6 month European put option on the mining company BHP at an exercise price of $40 for a premium of $3.
Which of the following statements best describes your situation?
Below are 4 option graphs. Note that the y-axis is payoff at maturity (T). What options do they depict? List them in the order that they are numbered
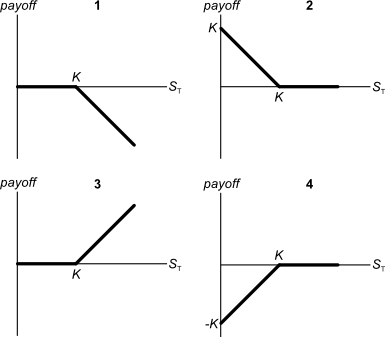
You operate a cattle farm that supplies hamburger meat to the big fast food chains. You buy a lot of grain to feed your cattle, and you sell the fully grown cattle on the livestock market.
You're afraid of adverse movements in grain and livestock prices. What options should you buy to hedge your exposures in the grain and cattle livestock markets?
Select the most correct response:
Suppose that the US government recently announced that subsidies for fresh milk producers will be gradually phased out over the next year. Newspapers say that there are expectations of a 40% increase in the spot price of fresh milk over the next year.
Option prices on fresh milk trading on the Chicago Mercantile Exchange (CME) reflect expectations of this 40% increase in spot prices over the next year. Similarly to the rest of the market, you believe that prices will rise by 40% over the next year.
What option trades are likely to be profitable, or to be more specific, result in a positive Net Present Value (NPV)?
Assume that:
- Only the spot price is expected to increase and there is no change in expected volatility or other variables that affect option prices.
- No taxes, transaction costs, information asymmetry, bid-ask spreads or other market frictions.
Question 271 CAPM, option, risk, systematic risk, systematic and idiosyncratic risk
All things remaining equal, according to the capital asset pricing model, if the systematic variance of an asset increases, its required return will increase and its price will decrease.
If the idiosyncratic variance of an asset increases, its price will be unchanged.
What is the relationship between the price of a call or put option and the total, systematic and idiosyncratic variance of the underlying asset that the option is based on? Select the most correct answer.
Call and put option prices increase when the:
Which one of the following is NOT usually considered an 'investable' asset for long-term wealth creation?
You believe that the price of a share will fall significantly very soon, but the rest of the market does not. The market thinks that the share price will remain the same. Assuming that your prediction will soon be true, which of the following trades is a bad idea? In other words, which trade will NOT make money or prevent losses?
Question 381 Merton model of corporate debt, option, real option
In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying risk free government bonds and:
Question 382 Merton model of corporate debt, real option, option
In the Merton model of corporate debt, buying a levered company's shares is equivalent to:
Question 383 Merton model of corporate debt, real option, option
In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying the company's assets and:
Which of the following is the least useful method or model to calculate the value of a real option in a project?
Question 385 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The levered equity graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?
Question 386 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The risky corporate debt graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?
One of the reasons why firms may not begin projects with relatively small positive net present values (NPV's) is because they wish to maximise the value of their:
A moped is a bicycle with pedals and a little motor that can be switched on to assist the rider. Mopeds are useful for quick transport using the motor, and for physical exercise when using the pedals unassisted. This offers the rider:
You're thinking of starting a new cafe business, but you're not sure if it will be profitable.
You have to decide what type of cups, mugs and glasses you wish to buy. You can pay to have your cafe's name printed on them, or just buy the plain un-marked ones. For marketing reasons it's better to have the cafe name printed. But the plain un-marked cups, mugs and glasses maximise your:
Some financially minded people insist on a prenuptial agreement before committing to marry their partner. This agreement states how the couple's assets should be divided in case they divorce. Prenuptial agreements are designed to give the richer partner more of the couples' assets if they divorce, thus maximising the richer partner's:
The cheapest mobile phones available tend to be those that are 'locked' into a cell phone operator's network. Locked phones can not be used with other cell phone operators' networks.
Locked mobile phones are cheaper than unlocked phones because the locked-in network operator helps create a monopoly by:
Your firm's research scientists can begin an exciting new project at a cost of $10m now, after which there’s a:
- 70% chance that cash flows will be $1m per year forever, starting in 5 years (t=5). This is the A state of the world.
- 20% chance that cash flows will be $3m per year forever, starting in 5 years (t=5). This is the B state of the world.
- 10% chance of a major break through in which case the cash flows will be $20m per year forever starting in 5 years (t=5), or instead, the project can be expanded by investing another $10m (at t=5) which is expected to give cash flows of $60m per year forever, starting at year 9 (t=9). Note that the perpetual cash flows are either the $20m from year 4 onwards, or the $60m from year 9 onwards after the additional $10m year 5 investment, but not both. This is the C state of the world.
The firm's cost of capital is 10% pa.
What's the present value (at t=0) of the option to expand in year 5?
A European call option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the call option?
A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the put option?
A European call option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from having written (being short) the call option?
A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.
What is an expression for the payoff at maturity ##(f_T)## in dollars from having written (being short) the put option?
Question 432 option, option intrinsic value, no explanation
An American style call option with a strike price of ##K## dollars will mature in ##T## years. The underlying asset has a price of ##S## dollars.
What is an expression for the current intrinsic value in dollars from owning (being long) the American style call option? Note that the intrinsic value of an option does not subtract the premium paid to buy the option.
Question 433 Merton model of corporate debt, real option, option, no explanation
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.
What is the payoff to equity holders at maturity, assuming that they keep their shares until maturity?
Question 434 Merton model of corporate debt, real option, option
A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:
##V## = Market value of assets.
##E## = Market value of (levered) equity.
##D## = Market value of zero coupon bonds.
##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.
What is the payoff to debt holders at maturity, assuming that they keep their debt until maturity?
Question 584 option, option payoff at maturity, option profit
Which of the following statements about European call options on non-dividend paying stocks is NOT correct?
A man just sold a call option to his counterparty, a lady. The man has just now:
Which of the following statements about option contracts is NOT correct? For every:
If trader A has sold the right that allows counterparty B to buy the underlying asset from him at maturity if counterparty B wants then trader A is:
After doing extensive fundamental analysis of a company, you believe that their shares are overpriced and will soon fall significantly. The market believes that there will be no such fall.
Which of the following strategies is NOT a good idea, assuming that your prediction is true?
Question 636 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being long a call option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Question 637 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being short a call option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Question 638 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being long a put option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Question 639 option, option payoff at maturity, no explanation
Which of the below formulas gives the payoff ##(f)## at maturity ##(T)## from being short a put option? Let the underlying asset price at maturity be ##S_T## and the exercise price be ##X_T##.
Which one of the below option and futures contracts gives the possibility of potentially unlimited gains?
A trader buys one crude oil European style call option contract on the CME expiring in one year with an exercise price of $44 per barrel for a price of $6.64. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before maturity, then at maturity she will have the:
Which of the below formulas gives the profit ##(\pi)## from being long a call option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LC,0}##. Note that ##S_T##, ##X_T## and ##f_{LC,0}## are all positive numbers.
Which of the below formulas gives the profit ##(\pi)## from being short a call option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LC,0}##. Note that ##S_T##, ##X_T## and ##f_{LC,0}## are all positive numbers.
Which of the below formulas gives the profit ##(\pi)## from being long a put option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LP,0}##. Note that ##S_T##, ##X_T## and ##f_{LP,0}## are all positive numbers.
Which of the below formulas gives the profit ##(\pi)## from being short a put option? Let the underlying asset price at maturity be ##S_T##, the exercise price be ##X_T## and the option price be ##f_{LP,0}##. Note that ##S_T##, ##X_T## and ##f_{LP,0}## are all positive numbers.
A trader sells one crude oil European style call option contract on the CME expiring in one year with an exercise price of $44 per barrel for a price of $6.64. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before maturity, then at maturity she will have the:
A trader buys one crude oil European style put option contract on the CME expiring in one year with an exercise price of $44 per barrel for a price of $6.64. The crude oil spot price is $40.33. If the trader doesn’t close out her contract before maturity, then at maturity she will have the:
Which of the following statements about call options is NOT correct?
A trader just bought a European style put option on CBA stock. The current option premium is $2, the exercise price is $75, the option matures in one year and the spot CBA stock price is $74.
Which of the following statements is NOT correct?
Question 793 option, hedging, delta hedging, gamma hedging, gamma, Black-Scholes-Merton option pricing
A bank buys 1000 European put options on a $10 non-dividend paying stock at a strike of $12. The bank wishes to hedge this exposure. The bank can trade the underlying stocks and European call options with a strike price of 7 on the same stock with the same maturity. Details of the call and put options are given in the table below. Each call and put option is on a single stock.
| European Options on a Non-dividend Paying Stock | |||
| Description | Symbol | Put Values | Call Values |
| Spot price ($) | ##S_0## | 10 | 10 |
| Strike price ($) | ##K_T## | 12 | 7 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.4 | 0.4 |
| Option maturity (years) | ##T## | 1 | 1 |
| Option price ($) | ##p_0## or ##c_0## | 2.495350486 | 3.601466138 |
| ##N[d_1]## | ##\partial c/\partial S## | 0.888138405 | |
| ##N[d_2]## | ##N[d_2]## | 0.792946442 | |
| ##-N[-d_1]## | ##\partial p/\partial S## | -0.552034778 | |
| ##N[-d_2]## | ##N[-d_2]## | 0.207053558 | |
| Gamma | ##\Gamma = \partial^2 c/\partial S^2## or ##\partial^2 p/\partial S^2## | 0.098885989 | 0.047577422 |
| Theta | ##\Theta = \partial c/\partial T## or ##\partial p/\partial T## | 0.348152078 | 0.672379961 |
Which of the following statements is NOT correct?
Question 794 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the Delta of a European call option?
Where:
###d_1=\dfrac{\ln[S_0/K]+(r+\sigma^2/2).T)}{\sigma.\sqrt{T}}### ###d_2=d_1-\sigma.\sqrt{T}=\dfrac{\ln[S_0/K]+(r-\sigma^2/2).T)}{\sigma.\sqrt{T}}###Question 795 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the Delta of a European put option?
Question 796 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European call option will be exercised?
Question 797 option, Black-Scholes-Merton option pricing, option delta, no explanation
Which of the following quantities from the Black-Scholes-Merton option pricing formula gives the risk-neutral probability that a European put option will be exercised?
Which derivatives position has the possibility of unlimited potential gains?
Which of the following terms about options are NOT synonyms?
What derivative position are you exposed to if you have the obligation to sell the underlying asset at maturity, so you will definitely be forced to sell the underlying asset?
Question 821 option, option profit, option payoff at maturity, no explanation
You just paid $4 for a 3 month European style call option on a stock currently priced at $47 with a strike price of $50. The stock’s next dividend will be $1 in 4 months’ time. Note that the dividend is paid after the option matures. Which of the below statements is NOT correct?
When does a European option's last-traded market price become a sunk cost?
Question 823 option, option payoff at maturity, option profit, no explanation
A European call option should only be exercised if:
A put option written on a risky non-dividend paying stock will mature in one month. As is normal, assume that the option's exercise price is non-zero and positive ##(K>0)## and the stock has limited liability ##(S>0)##.
Which of the following statements is NOT correct? The put option's:
Question 829 option, future, delta, gamma, theta, no explanation
Below are some statements about futures and European-style options on non-dividend paying stocks. Assume that the risk free rate is always positive. Which of these statements is NOT correct? All other things remaining equal:
Below are some statements about European-style options on non-dividend paying stocks. Assume that the risk free rate is always positive. Which of these statements is NOT correct?
Question 831 option, American option, no explanation
Which of the following statements about American-style options is NOT correct? American-style:
A 12 month European-style call option with a strike price of $11 is written on a dividend paying stock currently trading at $10. The dividend is paid annually and the next dividend is expected to be $0.40, paid in 9 months. The risk-free interest rate is 5% pa continuously compounded and the standard deviation of the stock’s continuously compounded returns is 30 percentage points pa. The stock's continuously compounded returns are normally distributed. Using the Black-Scholes-Merton option valuation model, determine which of the following statements is NOT correct.
Question 833 option, delta, theta, standard deviation, no explanation
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
Question 834 option, delta, theta, gamma, standard deviation, Black-Scholes-Merton option pricing
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
| European Call Option | ||
| on a non-dividend paying stock | ||
| Description | Symbol | Quantity |
| Spot price ($) | ##S_0## | 20 |
| Strike price ($) | ##K_T## | 18 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.3 |
| Option maturity (years) | ##T## | 1 |
| Call option price ($) | ##c_0## | 3.939488 |
| Delta | ##\Delta = N[d_1]## | 0.747891 |
| ##N[d_2]## | ##N[d_2]## | 0.643514 |
| Gamma | ##\Gamma## | 0.053199 |
| Theta ($/year) | ##\Theta = \partial c / \partial T## | 1.566433 |
Being long a call and short a put which have the same exercise prices and underlying stock is equivalent to being:
A stock, a call, a put and a bond are available to trade. The call and put options' underlying asset is the stock they and have the same strike prices, ##K_T##.
Being long the call and short the stock is equivalent to being:
A stock, a call, a put and a bond are available to trade. The call and put options' underlying asset is the stock they and have the same strike prices, ##K_T##.
You are currently long the stock. You want to hedge your long stock position without actually trading the stock. How would you do this?
A one year European-style call option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The call option price now is:
A one year European-style put option has a strike price of $4. The option's underlying stock pays no dividends and currently trades at $5. The risk-free interest rate is 10% pa continuously compounded. Use a single step binomial tree to calculate the option price, assuming that the price could rise to $8 ##(u = 1.6)## or fall to $3.125 ##(d = 1/1.6)## in one year. The put option price now is:
A one year European-style call option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
A one year European-style put option has a strike price of $4.
The option's underlying stock currently trades at $5, pays no dividends and its standard deviation of continuously compounded returns is 47% pa.
The risk-free interest rate is 10% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The put option price now is:
Question 903 option, Black-Scholes-Merton option pricing, option on stock index
A six month European-style call option on the S&P500 stock index has a strike price of 2800 points.
The underlying S&P500 stock index currently trades at 2700 points, has a continuously compounded dividend yield of 2% pa and a standard deviation of continuously compounded returns of 25% pa.
The risk-free interest rate is 5% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
Question 904 option, Black-Scholes-Merton option pricing, option on future on stock index
A six month European-style call option on six month S&P500 index futures has a strike price of 2800 points.
The six month futures price on the S&P500 index is currently at 2740.805274 points. The futures underlie the call option.
The S&P500 stock index currently trades at 2700 points. The stock index underlies the futures. The stock index's standard deviation of continuously compounded returns is 25% pa.
The risk-free interest rate is 5% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
A non-dividend paying stock has a current price of $20.
The risk free rate is 5% pa given as a continuously compounded rate.
Options on the stock are currently priced at $5 for calls and $5.55 for puts where both options have a 2 year maturity and an exercise price of $24.
You suspect that the call option contract is mis-priced and would like to conduct a risk-free arbitrage that requires zero capital. Which of the following steps about arbitraging the situation is NOT correct?
Question 954 option, at the money option
Question 956 option, Black-Scholes-Merton option pricing, delta hedging, hedging
A bank sells a European call option on a non-dividend paying stock and delta hedges on a daily basis. Below is the result of their hedging, with columns representing consecutive days. Assume that there are 365 days per year and interest is paid daily in arrears.
| Delta Hedging a Short Call using Stocks and Debt | |||||||
| Description | Symbol | Days to maturity (T in days) | |||||
| 60 | 59 | 58 | 57 | 56 | 55 | ||
| Spot price ($) | S | 10000 | 10125 | 9800 | 9675 | 10000 | 10000 |
| Strike price ($) | K | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 |
| Risk free cont. comp. rate (pa) | r | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | σ | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| Option maturity (years) | T | 0.164384 | 0.161644 | 0.158904 | 0.156164 | 0.153425 | 0.150685 |
| Delta | N[d1] = dc/dS | 0.552416 | 0.582351 | 0.501138 | 0.467885 | 0.550649 | 0.550197 |
| Probability that S > K at maturity in risk neutral world | N[d2] | 0.487871 | 0.51878 | 0.437781 | 0.405685 | 0.488282 | 0.488387 |
| Call option price ($) | c | 685.391158 | 750.26411 | 567.990995 | 501.487157 | 660.982878 | ? |
| Stock investment value ($) | N[d1]*S | 5524.164129 | 5896.301781 | 4911.152036 | 4526.788065 | 5506.488143 | ? |
| Borrowing which partly funds stock investment ($) | N[d2]*K/e^(r*T) | 4838.772971 | 5146.037671 | 4343.161041 | 4025.300909 | 4845.505265 | ? |
| Interest expense from borrowing paid in arrears ($) | r*N[d2]*K/e^(r*T) | 0.662891 | 0.704985 | 0.594994 | 0.551449 | ? | |
| Gain on stock ($) | N[d1]*(SNew - SOld) | 69.052052 | -189.264008 | -62.642245 | 152.062648 | ? | |
| Gain on short call option ($) | -1*(cNew - cOld) | -64.872952 | 182.273114 | 66.503839 | -159.495721 | ? | |
| Net gain ($) | Gains - InterestExpense | 3.516209 | -7.695878 | 3.266599 | -7.984522 | ? | |
| Gamma | Γ = d^2c/dS^2 | 0.000244 | 0.00024 | 0.000255 | 0.00026 | 0.000253 | 0.000255 |
| Theta | θ = dc/dT | 2196.873429 | 2227.881353 | 2182.174706 | 2151.539751 | 2266.589184 | 2285.1895 |
In the last column when there are 55 days left to maturity there are missing values. Which of the following statements about those missing values is NOT correct?