The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
###\begin{aligned} NPV &= C_0 + \frac{C_2}{(1+r)^2} \\ &= -100 + \frac{121}{(1+0.1)^2} \\ &= -100 + 100 \\ &= 0 \\ \end{aligned}###
What is the Internal Rate of Return (IRR) of the project detailed in the table below?
Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
###\begin{aligned} 0 &= C_0 + \frac{C_2}{(1+r_\text{IRR})^2} \\ &= -100 + \frac{121}{(1+r_\text{IRR})^2} \\ \end{aligned}###
###(1+r_\text{IRR})^2 = \frac{121}{100} ######\begin{aligned} r_\text{IRR} &= \left( \frac{121}{100} \right)^{1/2} - 1 \\ &= 0.1 \\ \end{aligned}###
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
By definition, the Internal Rate of Return (IRR) is the particular required return that makes the project's Net Present Value (NPV) equal to zero.
###\begin{aligned} NPV &= C_0 + \frac{C_1}{(1+r_\text{required})^1} + \frac{C_2}{(1+r_\text{required})^2} + ... + \frac{C_T}{(1+r_\text{required})^T} \\ 0 &= C_0 + \frac{C_1}{(1+r_{irr})^1} + \frac{C_2}{(1+r_{irr})^2} + ... + \frac{C_T}{(1+r_{irr})^T} \\ \end{aligned} ###
Therefore if the NPV is zero then the IRR must be equal to the required return.
The required return of a building project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
The building firm is just about to start the project and the client has signed the contract. Initially the firm will pay $100 to the sub-contractors to carry out the work and then will receive an $11 payment from the client in one year and $121 when the project is finished in 2 years. Ignore credit risk.
But the building company is considering selling the project to a competitor at different points in time and is pondering the minimum price that they should sell it for.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
Which of the below statements is NOT correct? The project is worth:
All assets are worth the present value of the future cash flows, so at 1.5 years, the only cash flow left is the $121 in year 2 which is half a year away. Therefore the value of the project is the present value of $121 over half a year.:
###\begin{aligned} V_{1.5} &= \frac{C_2}{(1+r)^{0.5}} \\ &= \frac{121}{(1+0.1)^{0.5}} \\ &= 115.3689733 \\ \end{aligned}###
This is the minimum price that the building company should sell the project for in 1.5 years.
You might think that the firm have only completed half of the second year's work at t=1.5, so they only deserve half of the payment of $121. But remember that the value of an asset is the present value of future cash flows. We're not accountants recording the work in progress in the past. The market value now is the present value of future cash flows.
We paid the sub-contractors at t=0 and they promised to complete the work. The client promised to pay the $121 at time 2. So as long as there's no credit risk that the clients don't pay or the sub-contractors don't do their work, the project is worth the present value of the future cash flows.
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
Table method:
| Payback Period Calculation | ||
| Time (yrs) |
Cash flow ($) |
Cumulative cash flow ($) |
| 0 | -100 | -100 |
| 1 | 11 | -89 |
| 2 | 121 | 32 |
The payback period ##T_\text{payback}## is then the time at which the first positive cumulative cash flow occurs, less the cumulative cash flow divided by the single cash flow in that period:
###\begin{aligned} T_\text{payback} &= \left( \begin{array}{c} \text{time of} \\ \text{first positive} \\ \text{cumulative} \\ \text{cash flow} \\ \end{array} \right) - \frac{ \left( \begin{array}{c} \text{first positive} \\ \text{cumulative} \\ \text{cash flow} \\ \end{array} \right) }{ \left( \begin{array}{c} \text{cash flow over} \\ \text{that period} \\ \end{array} \right) } \\ &= 2 - \frac{32}{121} \\ &= 2 - \frac{32}{121} \\ &= 2 - 0.26446281 \\ &= 1.73553719 \text{ yrs} \\ \end{aligned}###
Quick method: A table might be overkill for this simple project, the payback period clearly occurs sometime during the second year (between t=1 and 2), so
###\begin{aligned} T_\text{payback} &= 2 - \frac{-100 + 11 + 121}{121} \\ &= 2 - \frac{32}{121} \\ &= 1.73553719 \text{ yrs} \\ \end{aligned}###
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
What is the payback period of the project in years?
Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $500 at time 2 is actually earned smoothly from t=1 to t=2.
To find the payback period,
###\begin{aligned} T_\text{payback} &= \left( \begin{array}{c} \text{time of} \\ \text{first positive} \\ \text{cumulative} \\ \text{cash flow} \\ \end{array} \right) - \frac{ \left( \begin{array}{c} \text{first positive} \\ \text{cumulative} \\ \text{cash flow} \\ \end{array} \right) }{ \left( \begin{array}{c} \text{cash flow over} \\ \text{that period} \\ \end{array} \right) } \\ &= 2 - \frac{(-400+500)}{500} \\ &= 2 - \frac{100}{500} \\ &= 1.8 \\ \end{aligned} ###
The below graph shows a project's net present value (NPV) against its annual discount rate.
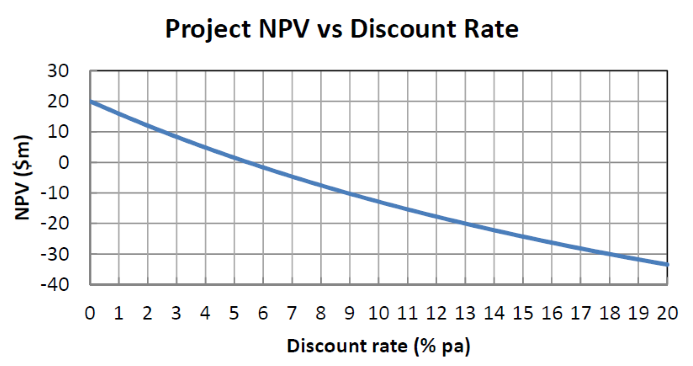
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
Projects add to the firm's asset value if their net present value (NPV) of cash flows is positive, which in this case occurs between the discount rates of zero to five percent. The positive NPV can be seen on the graph where the blue line is above above zero on the vertical y-axis which represents the NPV.
The below graph shows a project's net present value (NPV) against its annual discount rate.

Which of the following statements is NOT correct?
The project's payback period is not infinite, it must be a finite amount of years because when the discount rate is zero, the NPV is $20m as can be seen from the graph. Therefore the sum of the cash flows is positive, so the project must eventually pay itself off.
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
Let ##C_t## be consumption at time t and ##V_t## be wealth at time t.
Common sense method:
We initially have ##V_0## wealth in the bank. Then we consume or spend ##C_0## a moment later, still at time zero. The amount left in the bank accrues interest so it grows over the next year by the interest rate. To find this future value we multiply by ##(1+r)^1##. At time one, everything that's left in the bank is consumed ##(C_1)## with nothing left over at the end.
###(V_0 -C_0)(1+r)^1 - C_1 = 0 ###| Formula Building Steps | ||
| Time | Event | Formula |
| 0 | Starting wealth | ##V_0## |
| 0 | Consume | ##V_0 - C_0## |
| 1 | Lend to bank for one year | ##(V_0 - C_0)(1+r)^1## |
| 1 | Consume all so there's nothing left | ##(V_0 - C_0)(1+r)^1 - C_1 = 0## |
The question stated that consumption at t=0 and t=1 are equal, so ##C_0 = C_1 ##. So we can solve simultaneously and substitute numbers (k represents thousands),
###(V_0 -C_0)(1+r)^1 - C_1 = 0 ### ###(V_0 -C_0)(1+r)^1 - C_\color{red}{0} = 0 ### ###(100k -C_0)(1+0.1)^1 - C_0 = 0 ### ###100k(1+0.1)^1 -C_0(1+0.1)^1 - C_0 = 0 ### ###C_0\left(1+(1+0.1)^1\right) = 100k(1+0.1)^1 ### ###\begin{aligned} C_0 &= \frac{100k(1+0.1)^1}{1+(1+0.1)^1} \\ &= \frac{100,000 \times 1.1}{2.1} \\ &= 52,380.9524 \\ \end{aligned}### ###C_1 = C_0 = 52,380.9524###Present value method:
This method is easier to formulate. Since all wealth will be consumed, the present value of the positive wealth and negative consumption must equal zero.
###V_0 -C_0 - \frac{C_1}{(1+r)^1} +\frac{V_1}{(1+r)^1} = 0 ###The question stated that consumption at t=0 and t=1 are equal, so ##C_0 = C_1 ##. Also ##V_1 = 0## since there's no wealth left over at the end.
Solving simultaneously and substituting numbers (k represents thousands),
###100k -C_0 - \frac{C_0}{(1+0.1)^1} +\frac{0}{(1+0.1)^1} = 0 ### ###C_0\left(1+ \frac{1}{(1+0.1)^1}\right) = 100k ### ###\begin{aligned} C_0 &= \frac{100k}{\left(1+ \frac{1}{(1+0.1)^1}\right)} \\ &= 52,380.9524 = C_1 \\ \end{aligned}###Future value method:
Similarly to the present value method, this method is easy to formulate. Since all wealth will be consumed, the future value of the positive wealth and negative consumption must equal zero.
###V_0(1+r)^1 -C_0(1+r)^1 - C_1 = 0 ###The question stated that consumption at t=0 and t=1 are equal, so ##C_0 = C_1 ##.
Solving simultaneously and substituting numbers (k represents thousands),
###100k(1+0.1)^1 -C_0(1+0.1)^1 - C_0 = 0 ### ###C_0\left(1+ \frac{1}{(1+0.1)^1}\right) = 100k ### ###C_0 = 52,380.9524 = C_1 ###You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
Let ##C_t## be consumption at time t and ##V_t## be wealth at time t.
Common sense method:
We have ##V_0## in the bank then we consume ##C_0## of that at time zero. The amount left in the bank accrues interest over the year so we grow it by ##(1+r)^1##. Again at time one we consume ##C_1##, and the amount remaining in the bank accrues more interest. At time two we consume ##C_2## and the amount left after this is ##V_2##.
###\left( (V_0 -C_0)(1+r)^1 - C_1 \right)(1+r)^1-C_2 = V_2 ###| Formula Building Steps | ||
| Time | Event | Formula |
| 0 | Starting wealth | ##V_0## |
| 0 | Consume | ##V_0 - C_0## |
| 1 | Lend to bank for one year | ##(V_0 - C_0)(1+r)^1## |
| 1 | Consume more | ##(V_0 - C_0)(1+r)^1 - C_1## |
| 2 | Lend to bank for another year | ##((V_0 - C_0)(1+r)^1 - C_1)(1+r)^1## |
| 2 | Consume again but leave some wealth aside | ##((V_0 - C_0)(1+r)^1 - C_1)(1+r)^1 - C_2 = V_2## |
The question stated that consumption at t=0,1 and 2 are equal, so ##C_0 = C_1 = C_2##.
Solving simultaneously and substituting numbers (k represents thousands),
###\left( (V_0 -C_0)(1+r)^1 - C_1 \right)(1+r)^1-C_2 = V_2 ### ###\left( (100k -C_0)(1+0.1)^1 - C_0 \right)(1+0.1)^1-C_0 = 50k ### ###\begin{aligned} C_0 &= \dfrac{100k(1+0.1)^2 - 50k }{1+(1+0.1)^1 + (1+0.1)^2} \\ &= 21,450.1511 = C_1 = C_2 \\ \end{aligned}###Present value method:
###V_0 -C_0 - \frac{C_1}{(1+r)^1} -\frac{C_2}{(1+r)^2}- \frac{V_2}{(1+r)^2}= 0 ###Also, consumption at t=0, 1 and 2 are all equal, so
###C_0 = C_1 = C_2 ###Solving simultaneously and substituting numbers (k represents thousands),
###100k -C_0 - \frac{C_0}{(1+r)^1} -\frac{C_0}{(1+r)^2} - \frac{50k}{(1+r)^2}= 0 ### ###C_0\left(1+ \frac{1}{(1+0.1)^1} + \frac{1}{(1+0.1)^2}\right) = 100k - \frac{50k}{(1+0.1)^2} ### ###\begin{aligned} C_0 &= \frac{100k - \dfrac{50k}{(1+0.1)^2}}{\left(1+ \dfrac{1}{(1+0.1)^1} + \dfrac{1}{(1+0.1)^2}\right)} \\ &= 21,450.1511 = C_1 = C_2 \\ \end{aligned}###Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
Right now (at t=0), borrow $109.09 from the bank and lend $100 of it to your neighbour now. This leaves us with a positive cash flow of $9.09 at t=0.
In on year (t=1), take the $120 from your neighbour and use it to pay back the bank the $120 owed ##\left(109.09\times(1+0.1)^1\right)##. This leaves us with a cash flow of zero at t=1.
To work out the amounts, use an arbitrage table.
| Arbitrage Table of Cash Flows | ||
| Instrument | Time 0 | Time 1 |
| Buy debt from (lend to) neighbour now, and wait for repayment in one year. | -100 | 120 |
| Sell debt to (borrow from) bank at 10% pa and pay it back in one year. | 109.09 Step 3 |
-120 Step 2 |
| Total | 9.09 Step 4 |
0 Step 1 |
The steps used to calculate the table's values are given here.
Step 1: All future cash flows need to total zero, that way only the initial (t=0) cash flow will be non-zero.
Step 2: The bank loan cash flow at time 1 must equal -120 so that total cash flows are zero. Since we're paying this $120 at the end, we must be borrowing using this bank loan.
Step 3: Since we're paying back 120 in one year, we must be borrowing the present value of that which is 109.09, calculated as follows: ###V_0 = -\dfrac{C_1}{(1+r)^1} = -\dfrac{-120}{(1+0.1)^1} = 109.09###
Step 4: Adding up the total cash flows at time zero, -100+109.09 = 9.09 which is the NPV of the arbitrage.
Arbitrage tables are great since they show how to a create a positive arbitrage cash flow of the NPV right now ($9.09) with no risk and no capital required.
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
The best project appears to be the car park because it has the highest IRR. But the other important decision criteria is NPV which isn't calculated. The NPV's are:
###V_\text{0, Petrol station} = -9,000,000 + \dfrac{11,000,000}{(1+0.1)^1} = 1,000,000 ### ###V_\text{0, Car wash} = -800,000 + \dfrac{1,100,000}{(1+0.1)^1} = 200,000 ### ###V_\text{0, Car park} = -70,000 + \dfrac{110,000}{(1+0.1)^1} = 30,000 ###So while the car park has the highest IRR, it has the lowest NPV. The petrol station has the highest NPV, but lowest IRR.
Because the projects are mutually exclusive, only one project can be chosen. Rationally it's best to make the most money and choose the project with the highest NPV. After all, would you prefer to make $30,000 on the car park, or 1 millions of dollars on the petrol station?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
Since the projects are mutually exclusive, the one with the highest NPV ##(V_0)## should be chosen.
###V_\text{0, Rent as is} = -900k + \dfrac{990k}{(1+0.1)^1} = 0### ###V_\text{0, Refurbish into offices} = -2m + \dfrac{2.4m}{(1+0.1)^1} = 0.1818m### ###V_\text{0, Convert to residential} = -3m + \dfrac{3.4m}{(1+0.1)^1} = 0.0909m###The refurbishment into modern offices has the highest NPV, so that's the best option. In this case it also has the highest IRR but that is a co-incidence. The best project is the one which makes the most wealth and that is best decided according to NPV.
Question 579 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to double if the price grows by 10% pa?
Use the 'present value of a single cash flow' formula to find the time taken for the price to double at the capital return of 10% pa.
###P_0 = \dfrac{P_t}{(1+0.1)^t} ###For the price to double, then ##P_{t}## will be twice ##P_0##, so ##P_{t} = 2P_0##. Substitute this into the above equation and solve for the time.
###P_0 = \dfrac{2P_0}{(1+0.1)^t} ### ###1 = \dfrac{2}{(1+0.1)^t} ### ###(1+0.1)^t = 2 ### ###\ln\left((1+0.1)^t\right) = \ln(2) ### ###t.\ln(1+0.1) = \ln(2) ### ###\begin{aligned} t &= \dfrac{\ln(2)}{\ln(1+0.1)} \\ &= 7.272540897 \text{ years} \\ \end{aligned}###Question 580 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to quadruple (be four times as big, say from $1 to $4) if the price grows by 15% pa?
Use the 'present value of a single cash flow' formula to find the time taken for the price to quadruple at the capital return of 15% pa.
###P_0 = \dfrac{P_t}{(1+0.15)^t} ###For the price to quadruple, then ##P_{t}## will be quadruple ##P_0##, so ##P_{t} = 4P_0##. Substitute this into the above equation and solve for the time.
###P_0 = \dfrac{4P_0}{(1+0.15)^t} ### ###1 = \dfrac{4}{(1+0.15)^t} ### ###(1+0.15)^t = 4 ### ###\ln\left((1+0.15)^t\right) = \ln(4) ### ###t.\ln(1+0.15) = \ln(4) ### ###\begin{aligned} t &= \dfrac{\ln(4)}{\ln(1+0.15)} \\ &= 9.918968909 \text{ years} \\ \end{aligned}###