A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.
What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
Question 239 income and capital returns, inflation, real and nominal returns and cash flows, interest only loan
A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.
From the bank's point of view, what is the long term expected nominal capital return of the loan asset?
In the dividend discount model:
### P_0= \frac{d_1}{r-g} ###
The pronumeral ##g## is supposed to be the:
Your firm's research scientists can begin an exciting new project at a cost of $10m now, after which there’s a:
- 70% chance that cash flows will be $1m per year forever, starting in 5 years (t=5). This is the A state of the world.
- 20% chance that cash flows will be $3m per year forever, starting in 5 years (t=5). This is the B state of the world.
- 10% chance of a major break through in which case the cash flows will be $20m per year forever starting in 5 years (t=5), or instead, the project can be expanded by investing another $10m (at t=5) which is expected to give cash flows of $60m per year forever, starting at year 9 (t=9). Note that the perpetual cash flows are either the $20m from year 4 onwards, or the $60m from year 9 onwards after the additional $10m year 5 investment, but not both. This is the C state of the world.
The firm's cost of capital is 10% pa.
What's the present value (at t=0) of the option to expand in year 5?
A man is thinking about taking a day off from his casual painting job to relax.
He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.
But he's thinking about the hours that he could work today (in the future) which are:
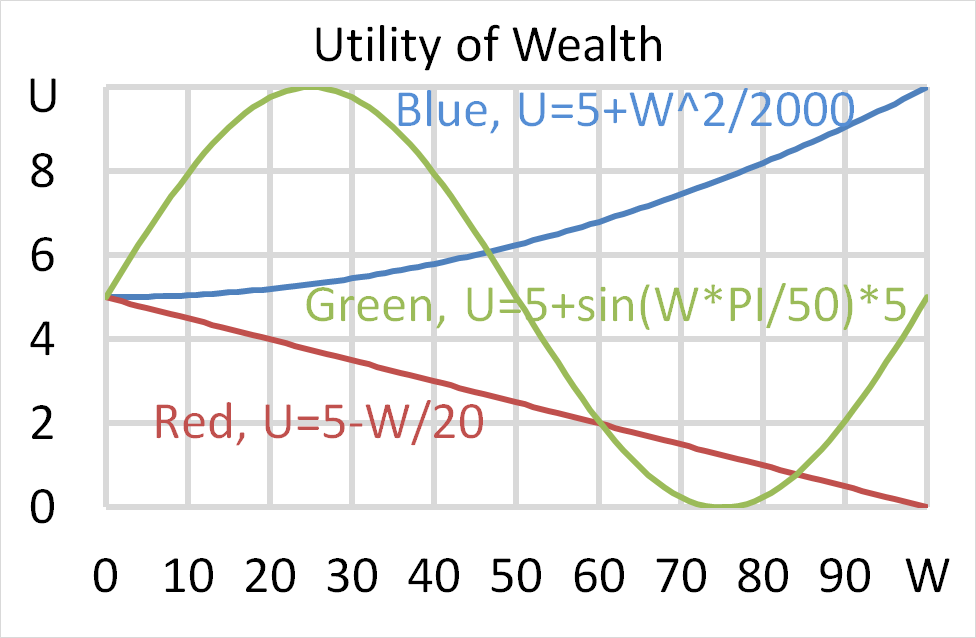
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
Question 803 capital raising, rights issue, initial public offering, on market repurchase, no explanation
Which one of the following capital raisings or payouts involve the sale of shares to existing shareholders only?
Question 834 option, delta, theta, gamma, standard deviation, Black-Scholes-Merton option pricing
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
| European Call Option | ||
| on a non-dividend paying stock | ||
| Description | Symbol | Quantity |
| Spot price ($) | ##S_0## | 20 |
| Strike price ($) | ##K_T## | 18 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.3 |
| Option maturity (years) | ##T## | 1 |
| Call option price ($) | ##c_0## | 3.939488 |
| Delta | ##\Delta = N[d_1]## | 0.747891 |
| ##N[d_2]## | ##N[d_2]## | 0.643514 |
| Gamma | ##\Gamma## | 0.053199 |
| Theta ($/year) | ##\Theta = \partial c / \partial T## | 1.566433 |