Which of the following statements about Macaulay duration is NOT correct? The Macaulay duration:
The Macaulay duration of a fixed-coupon bond will be less than or equal to the bond's maturity, not more. For zero coupon bonds, the duration will equal the maturity since all money is paid at the end. For coupon bonds, the coupons will pull the duration, the average time of payment, slightly lower than the maturity time when the big face value is paid.
Below is a table showing GMO's 2016 estimates of different assets' durations, appearing in Slater (2017).
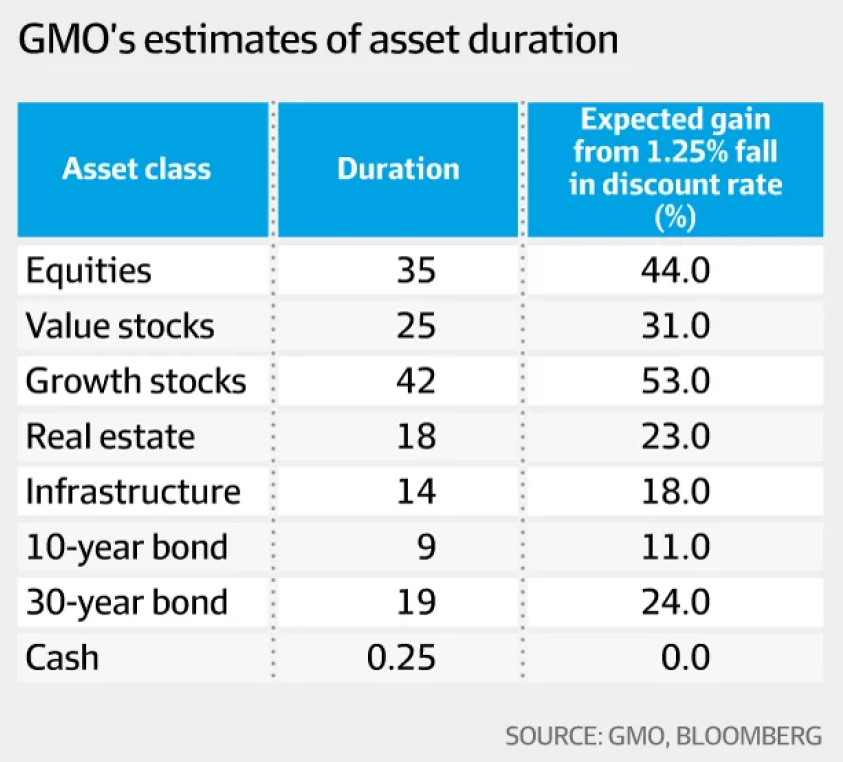
If you were certain that interest rates would fall more than the market expects, into what asset might you allocate more funds?
If interest rates fall, high-duration assets will increase in value the most. Therefore growth stocks will gain the most when interest rates fall, since they have the highest duration, which is the average time that payments are made, weighted by each payment. This is because growth stocks such as technology firms typically do not pay dividends or buybacks but rather re-invest in positive NPV projects.
Commentary
The third column 'Expected gain from 1.25% fall in discount rate' is simply negative one multiplied by the duration, multiplied by the change in yields -0.0125, with the old yield ##y_\text{old}## assumed to be zero:
###\begin{aligned} \text{CapitalReturn} = \%\Delta P &\approx -D_\text{Macaulay}.\dfrac{\Delta y}{1+y_\text{old}} \\ &\approx -42 \times \dfrac{0.0125}{1+0} \\ &\approx 0.53 = 53\% \\ \end{aligned}###This article by Slater (and GMO) is interesting because most of us learn about duration when studying bonds and aren't aware that it can be useful for thinking about stocks and real estate as well. To calculate the duration of a perpetuity ##(P_0 = C_1/(r-g))##, use this formula: ###\begin{aligned} D_\text{Macaulay} &= \frac{1+r}{r-g} \\ \end{aligned}###
Find the Macaulay duration of a 2 year 5% pa annual fixed coupon bond which has a $100 face value and currently has a yield to maturity of 8% pa. The Macaulay duration is:
The easiest way to do duration calculations is to use a table:
| Duration Calculations | |||
| 2 year 5% pa annual fixed coupon bond, $100 face value, 8% pa YTM | |||
| Time (years) | Cash flow ($) | Present value ($) | PV*t ($years) |
| ##t## | ##C_t## | ##PV(C_t)## | ##PV(C_t) \times t## |
| 1 | 5 | 4.62962963 | 4.62962963 |
| 2 | 105 | 90.02057613 | 180.0411523 |
| 94.65020576 | 184.6707819 | ||
| Duration: | 1.951086957 | ||
If you prefer to use the formulas without a table, here is the working:
###\begin{aligned} D_\text{Macaulay} &= \dfrac{\sum_{t=0}^{T} \left( t.\dfrac{C_t}{(1+y)^t} \right) }{ \sum_{t=0}^{T} \left( \dfrac{C_t}{(1+y)^t} \right) } = \dfrac{\sum_{t=0}^{T} \left( t.\dfrac{C_t}{(1+y)^t} \right) }{ P_0 } \\ &= \dfrac{\left( 1 \times \dfrac{5}{(1+0.08)^1} + 2 \times \dfrac{105}{(1+0.08)^2} \right)}{\left( \dfrac{5}{(1+0.08)^1} + \dfrac{105}{(1+0.08)^2} \right)} \\ &= \dfrac{\left( 1 \times 4.62962963 + 2 \times 90.02057613 \right)}{\left( 4.62962963 + 90.02057613 \right)} \\ &= \dfrac{184.6707819}{94.65020576} \\ &= 1.951086957 \text{ years}\\ \end{aligned}###Find the Macaulay duration of a 2 year 5% pa semi-annual fixed coupon bond which has a $100 face value and currently has a yield to maturity of 8% pa. The Macaulay duration is:
The easiest way to do duration calculations is to use a table:
| Duration Calculations | |||
| 2 year 5% pa semi-annual fixed coupon bond, $100 face value, 8% pa YTM | |||
| Time (years) | Cash flow ($) | Present value ($) | PV*t ($years) |
| ##t## | ##C_t## | ##PV(C_t)## | ##PV(C_t) \times t## |
| 0.5 | 2.5 | 2.403846154 | 1.201923077 |
| 1 | 2.5 | 2.311390533 | 2.311390533 |
| 1.5 | 2.5 | 2.222490897 | 3.333736345 |
| 2 | 102.5 | 87.61742958 | 175.2348592 |
| 94.55515716 | 182.0819091 | ||
| Duration: | 1.925668727 | ||
If you prefer to use the formulas without a table, here is the working:
###\begin{aligned} D_\text{Macaulay} &= \dfrac{\sum_{t=0}^{T} \left( t.\dfrac{C_t}{(1+y)^t} \right) }{ \sum_{t=0}^{T} \left( \dfrac{C_t}{(1+y)^t} \right) } = \dfrac{\sum_{t=0}^{T} \left( t.\dfrac{C_t}{(1+y)^t} \right) }{ P_0 } \\ &= \dfrac{\left( 0.5 \times \dfrac{2.5}{(1+0.08/2)^{0.5}} + 1 \times \dfrac{2.5}{(1+0.08/2)^{1}} + 1.5 \times \dfrac{2.5}{(1+0.08/2)^{1.5}} + 2 \times \dfrac{102.5}{(1+0.08/2)^{2}} \right)}{\left( \dfrac{2.5}{(1+0.08/2)^{0.5}} + \dfrac{2.5}{(1+0.08/2)^{1}} + \dfrac{2.5}{(1+0.08/2)^{1.5}} + \dfrac{102.5}{(1+0.08/2)^{2}} \right)} \\ &= \dfrac{\left( 0.5 \times 2.403846154 + 1 \times 2.311390533 + 1.5 \times 2.222490897 + 2 \times 87.61742958 \right)}{\left( 2.403846154 + 2.311390533 + 2.222490897 + 87.61742958 \right)} \\ &= \dfrac{182.0819091}{94.55515716} \\ &= 1.925668727 \text{ years}\\ \end{aligned}###Question 871 duration, Macaulay duration, modified duration, portfolio duration
Which of the following statements about Macaulay duration is NOT correct? The Macaulay duration:
The Macaulay duration of a portfolio is an arithmetic average of the Macaulay durations of the assets in the portfolio, weighted by their prices (present value of future cash flows), not face values.
Mathematically, the Macaulay duration of a portfolio ##D_p## containing ##n## assets with each asset ##i## having Macaulay duration ##D_i## with weight ##w_i## is: ###D_p = w_1.D_1 + w_2.D_2 + ... + w_n.D_n###
The modified duration ##(D^*## or ##D_\text{modified})## of a portfolio is equal to the Macaulay duration ##(D## or ##D_\text{Macaulay})## divided by (1+y), where y is the yield to maturity given as an effective annual rate and duration is measured in years. ###D_\text{modified} = \dfrac{D_\text{Macaulay}}{1+y_\text{eff annual}}###
The duration-price-change formulas give an approximation (##\approx## means approximately equal to) of the proportion change in bond price for a parallel shift up in the yield curve by ##\Delta y##:
###\begin{align} \text{ProportionalChangeInBondPrice} = \%\Delta P &\approx -D_\text{Macaulay}.\dfrac{\Delta y}{1+y} \\ &\approx -D_\text{modified}.\Delta y \\ \end{align}###Note that ##\Delta y## is measured in percentage points, so an increase in yields from 5% pa to 6% pa means that ##\Delta y## is 0.01 or 1 percentage point, not 20%.
A more specific version of the formula, where ##P_0## is the price now at time zero and ##P_1## is the price a moment later (not a year later) and duration is measured in years:
###\begin{align} \text{ProportionalChangeInBondPrice} = \dfrac{P_1 - P_0}{P_0} &\approx -D_\text{Macaulay}.\left( \dfrac{y_1 - y_0}{1+y_0} \right)\\ &\approx -D_\text{modified}.(y_1 - y_0) \\ \end{align}###Question 872 duration, Macaulay duration, modified duration, portfolio duration
A fixed coupon bond’s modified duration is 20 years, and yields are currently 10% pa compounded annually. Which of the following statements about the bond is NOT correct?
A zero-coupon bond's maturity must equal its Macaulay duration which is 22 years. This is because Macaulay duration is the weighted average time that an asset’s cash flows are received. For a zero coupon bond, the only cash flow is at maturity ##(T)## when the face value ##(F_T)## is paid.
For bonds in general that have cash flows ##C## which could be coupons or face values:
###D_\text{Macaulay} =\dfrac{\sum_{t=0}^{T} \left( t.\dfrac{C_t}{(1+y)^t} \right) }{ \sum_{t=0}^{T} \left( \dfrac{C_t}{(1+y)^t} \right) } = \dfrac{\sum_{t=0}^{T} \left( t.\dfrac{C_t}{(1+y)^t} \right) }{ P_0 }###For zero coupon bonds whose only cash flow is the face value ##(F_T)## at maturity ##(T)##:
###D_\text{Macaulay, zero coupon bond} = \dfrac{\left( T.\dfrac{F_t}{(1+y)^t} \right) }{ P_0 } = \dfrac{T.P_0}{ P_0 } = T###The modified duration ##(D^*## or ##D_\text{modified})## equals the Macaulay duration ##(D## or ##D_\text{Macaulay})## divided by (1+y), where y is the yield to maturity given as an effective annual rate and duration is measured in years:
###D_\text{modified} = \dfrac{D_\text{Macaulay}}{1+y_\text{eff annual}}### ###20 = \dfrac{D_\text{Macaulay}}{1+0.1}### ###\begin{aligned} D_\text{Macaulay} &= 20 \times (1+0.1) \\ &= 22 \text{ years}\\ \end{aligned}###Therefore the Macaulay duration is 22 years given that the modified duration is 20 years and yields to maturity are 10% given as effective annual rates.
Regarding answer options b and c:
Due to convexity, if yields-to-maturity suddenly:
- Fell by 1 percentage point then bond prices would suddenly rise by 20% or more;
- Rose by 1 percentage point then bond prices would suddenly fall by 20% or less.
Convexity is the curvature when plotting dollar bond price changes versus yield changes in percentage points. Convexity is valuable to bond-holders since convex bonds make dollar bond losses smaller and gains bigger when yields to maturity fall and rise respectively.
Question 918 duration, Macaulay duration, modified duration, bond convexity
A fixed coupon bond’s modified duration is 10 years, and yields are currently 5% pa compounded annually. Which of the following statements about the bond is NOT correct?
Due to convexity, if yields-to-maturity suddenly fell by 2 percentage points then bond prices would suddenly rise by 20% or more, not 20% or less. This is because convexity makes price gains bigger and price falls smaller than the linear duration-price-change approximation.
So while the duration-price-change formula says that if yields to maturity fall, then the linear approximate proportional price gain will be:
###\begin{align} \dfrac{\Delta P}{P_0} &\approx -D_\text{Macaulay}. \dfrac{\Delta y}{(1+y_0)} \\ \end{align}###But actually, if yields to maturity fall ##(\Delta y < 0)##, then the exact proportional price gain ##(\Delta P/P_0)##will be bigger (closer to positive infinity) than the linear duration approximation ##(-D_\text{Macaulay}.\Delta y / (1+y_0))##.
Similarly, if yields to maturity rise ##(\Delta y > 0)##, then the exact proportional price fall will also be closer to positive infinity than that given by the linear approximation.
###\begin{align} \dfrac{\Delta P}{P_0} \geq -D_\text{Macaulay}. \dfrac{\Delta y}{(1+y_0)} \\ \end{align}###This is good for investors, since assets with more convexity will gain more when rates fall and lose less when rates rise compared to assets with lower convexity.
Which of the following statements about bond convexity is NOT correct?
Bond issuers have bond liabilities, they sell bonds and will therefore have to pay back coupon and interest payments in the future.
It's true that bond holders (investors or lenders) like convexity, because if:
- yields rise, convex bonds lose less value than non-convex bonds of equal duration;
- yields fall, convex bonds gain more value than non-convex bonds of equal duration.
However, what's good for the asset holder (investor) must be bad for the liability holder (issuer), since the bond issuer owes the bond investor. Therefore bond issuers dislike convexity, it's bad for them.
Assume that the market portfolio has a duration of 15 years and an individual stock has a duration of 20 years.
What can you say about the stock's (single factor CAPM) beta with respect to the market portfolio? The stock's beta is likely to be:
The stock's higher duration means that it is likely to be more sensitive to changes in central bank interest rates than the market portfolio. Assuming that central bank monetary policy (interest rate) changes are systematically risky events, then higher sensitivity to these events due to higher duration would imply a higher required return and a higher CAPM beta.
Mathematically, a stock's CAPM beta equals:
###\beta_E = \sigma_{r_E, r_M} . \frac{\sigma_{r_E}}{\sigma_{r_M}} = correl(r_E, r_M) . \frac{sd(r_E)}{sd(r_M)}###The longer a stock's duration, the more sensitive it is to changes in interest rates, making its standard deviation ##sd(r_E)## higher, which is in the fraction's numerator, making its beta higher.
Also, the longer a stock's duration, the more correlated it is likely to be with the market portfolio, since the stock will react more strongly to surprise increases (or decreases) in interest rates, which affects the market portfolio in the same direction.
While this question specifically asks you to approach the problem from a single-factor CAPM framework, it's interesting to note that the effect of interest rate changes is often thought of as a whole separate factor in multi-factor CAPM's and arbitrage pricing theory (APT) models, which include the market portfolio factor in addition to others such as surprise interest rate changes. For example, here are five factors mentioned by Berry, Burmeister and McElroy (1988):
- risk of changes in default premiums;
- risk that the term structure of interest rates may change;
- risk of unanticipated inflation or deflation;
- risk that the long-run expected growth rate of profits for the economy will change; and
- residual market risk, or any remaining risk needed to explain a market index such as the S&P 500.
In the above list, factor 2 concerns interest rates while factor 5 is the market portfolio.
Which of the following assets would have the shortest duration?
The 90-day certificate of deposit (CD) pays no coupons, as is typical of money market securities, so it's equivalent to a zero coupon bond. Therefore its duration would equal its maturity which is 90 days. This duration is far shorter than the other securities whose durations would be years longer.
Note that this money market security's duration is not zero since the final payment in 90 days does not vary with any floating interest rate such as LIBOR or OIS, the final face value payment is fixed and written in the contract.
Question 999 duration, duration of a perpetuity with growth, CAPM, DDM
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the Macaulay duration of the stock now?
Starting with the CAPM's SML equation we can find the required return from the stock's beta, the market return and the risk free rate:
###\begin{aligned} r_E &= r_f + \beta_E(r_m-r_f) \\ &= 0.05 + 0.5(0.1-0.05) \\ &= 0.075 \\ \end{aligned} ###
Now that we have the total required return on equity, we can find the Macaulay duration using the 'duration of a perpetuity' formula where ##r## is the total required return:
###\begin{aligned} D_\text{Macaulay} &= \frac{1+r}{r-g} \\ &= \frac{1+0.075}{0.075-0.02} \\ &= 19.545455 \text{ years} \end{aligned}###So the weighted average time when you will receive your dividends is 19.545 years, weighted by the present value of all of the infinite number of dividends which stretch into perpetuity. It's interesting that the dividends and price are not needed in the formula.
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 3% pa and the market risk premium (MRP) is 6% pa. All returns are effective annual rates.
Which of the following statements is NOT correct?
If the Treasury bond yield were to fall 1 percentage point today, then the stock price is expected to rise by 25% approximately, ceteris paribus.
Which of the following statements about vanilla floating coupon bonds is NOT correct? A vanilla floating coupon bond's:
The benchmark rate used in a floating coupon bond is usually the London Interbank Offer Rate (LIBOR) or in Australia, the Bank Bill Swap Rate (BBSW). These rates change every day. Because of this, we say that these benchmark rates 'float', they're not fixed, since the rate is always changing, usually due to shifts in market expectations of future central bank monetary policy.
Which of the following statements about vanilla floating coupon bonds paying quarterly coupons is NOT correct? A vanilla floating coupon bond's:
A vanilla floating coupon bond's quarterly coupons following the first one, so that's coupon 2, 3, 4 and so on, are based on the benchmark rate at the time of the previous ex-coupon date. Therefore the next quarterly coupon is known for certain a quarter (3 months) in advance.
Due to the next coupon being fixed a quarter in advance, quarterly floating coupon bonds' Macaulay durations are equal to the time until that next coupon. This is because the bond's price is sensitive to changes in yields to maturity between now and the next coupon since the coupon (and price) is fixed for the remaining time. So an increase in a floating coupon bond's yield to maturity will cause it's price to fall.
Canaccord conducts a sensitivity analysis of the Israeli pharmaceutical firm InterCure's (INCR) estimated share price in figure 33 on page 30:
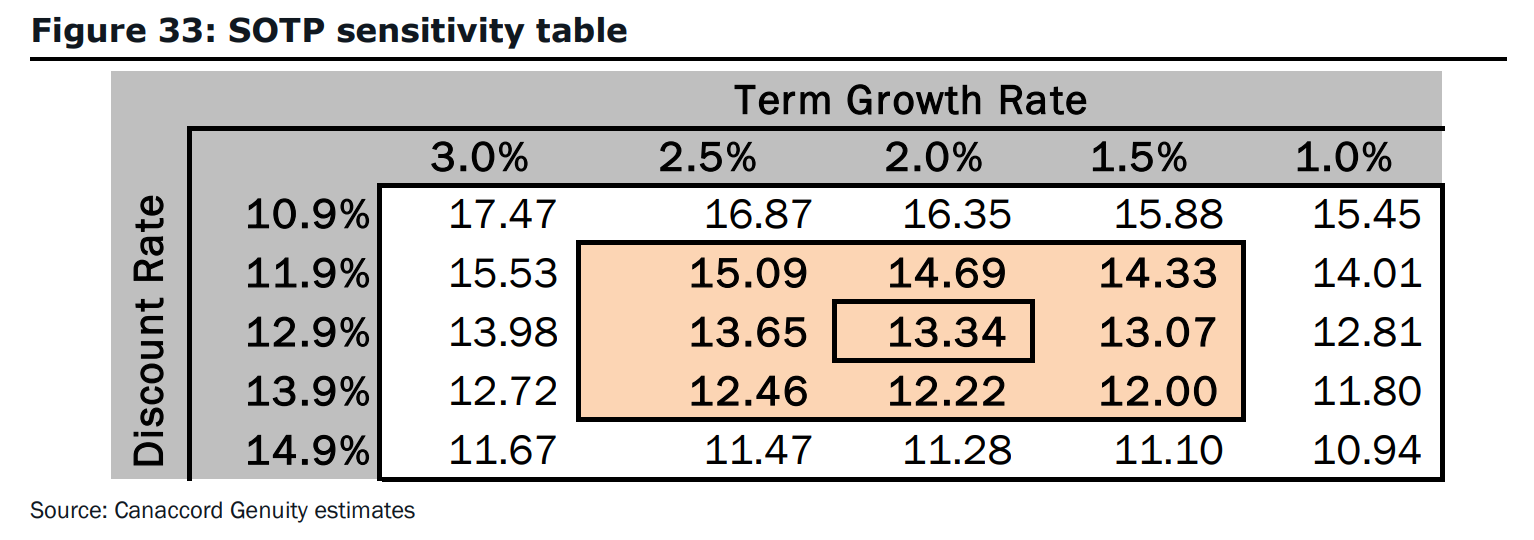
Estimate the Macaulay duration of INCR's equity. The Macaulay duration is approximately:
If the discount rate rate suddenly increased 1 percentage point from its current 12.9% pa 'base case' level to 13.9% pa, the share price will fall from $13.34 to $12.22, an 8.4% (=(12.22-13.34)/13.34) capital loss.
Using the duration-capital return formula, the approximate Macaulay duration can be estimated. Note that the squiggly equals ##\approx## means 'approximately equal':
###\dfrac{P_\text{new} - P_\text{old}}{P_\text{old}} \approx -D_\text{Macaulay}.\dfrac{\Delta y}{1+y}### ###\dfrac{12.22 - 13.34}{13.34} \approx -D_\text{Macaulay}.\dfrac{y_\text{new} - y_\text{old}}{1+y_\text{old}} ### ###-0.083958021 \approx -D_\text{Macaulay}.\dfrac{(0.139 - 0.129)}{(1+0.129)} ### ###-0.083958021 \approx -D_\text{Macaulay} \times 0.008857396 ### ###\begin{align} D_\text{Macaulay} \approx 9.47886057 \text{ years} \end{align}###Alternatively, the approximate Macaulay duration could be found by decreasing the discount rate by 1 percentage point from its current 12.9% pa 'base case' level to 11.9% pa, so the share price would rise from $13.34 to $14.69, a 10.12% (=(14.69-13.34)/13.34) capital gain, corresponding to a duration of 11.43 years (=0.1012/(0.01/(1+0.129))).