Question 871 duration, Macaulay duration, modified duration, portfolio duration
Which of the following statements about Macaulay duration is NOT correct? The Macaulay duration:
Question 872 duration, Macaulay duration, modified duration, portfolio duration
A fixed coupon bond’s modified duration is 20 years, and yields are currently 10% pa compounded annually. Which of the following statements about the bond is NOT correct?
Which of the following statements about Macaulay duration is NOT correct? The Macaulay duration:
Question 918 duration, Macaulay duration, modified duration, bond convexity
A fixed coupon bond’s modified duration is 10 years, and yields are currently 5% pa compounded annually. Which of the following statements about the bond is NOT correct?
Which of the following statements about bond convexity is NOT correct?
Find the Macaulay duration of a 2 year 5% pa annual fixed coupon bond which has a $100 face value and currently has a yield to maturity of 8% pa. The Macaulay duration is:
Find the Macaulay duration of a 2 year 5% pa semi-annual fixed coupon bond which has a $100 face value and currently has a yield to maturity of 8% pa. The Macaulay duration is:
Assume that the market portfolio has a duration of 15 years and an individual stock has a duration of 20 years.
What can you say about the stock's (single factor CAPM) beta with respect to the market portfolio? The stock's beta is likely to be:
Question 999 duration, duration of a perpetuity with growth, CAPM, DDM
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the Macaulay duration of the stock now?
Question 1000 duration, duration of a perpetuity with growth, needs refinement
An unlevered firm cuts its dividends and re-invests in zero-NPV projects with the same risk as its existing projects. This decreases the dividend yield, but increases the firm's equity's dividend growth rate and duration, while its total required return on equity remains unchanged. The equity can be valued as a perpetuity and the duration of a perpetuity is given below:
###D_\text{Macaulay} = \dfrac{1+r}{r-g}###What will be the effect on the stock's CAPM beta? Assume that there's no change in the risk free rate or market risk premium. The company's equity beta will:
Below is a table showing GMO's 2016 estimates of different assets' durations, appearing in Slater (2017).
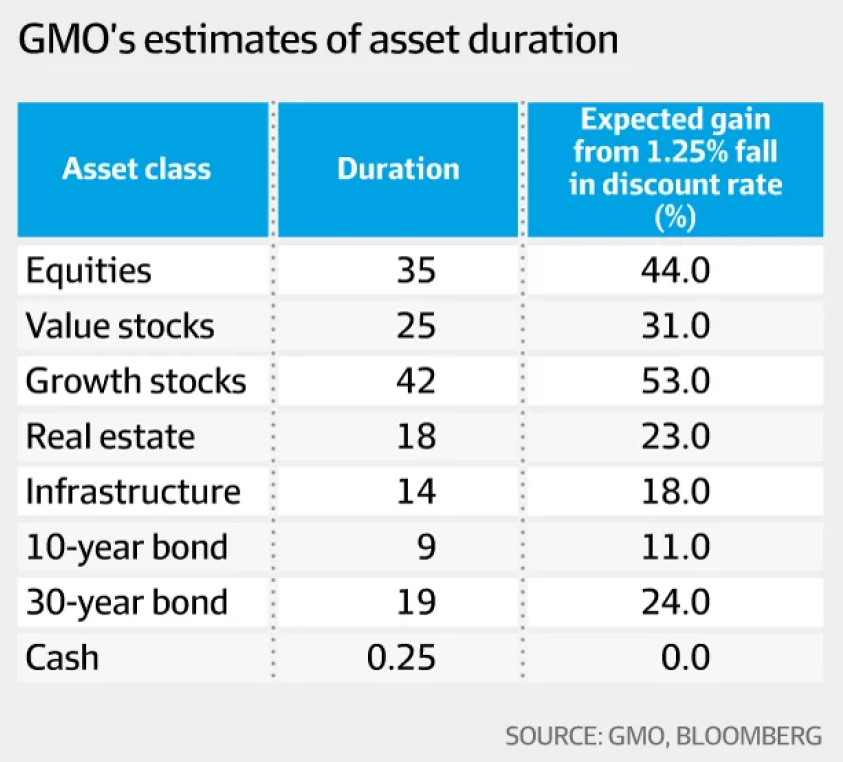
If you were certain that interest rates would fall more than the market expects, into what asset might you allocate more funds?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 3% pa and the market risk premium (MRP) is 6% pa. All returns are effective annual rates.
Which of the following statements is NOT correct?
Question 1034 duration, monetary policy, inflation, market efficiency
On 18 March 2022 the AFR's James Thomson wrote: "In a world where the bombs are still falling in Ukraine and the Fed is just getting started on what looks likely to be a year-long cycle of rising interest rates, it would take a certain amount of bravery to embrace the sort of high-tech, long duration plays that Wood favours" (Thomson, 2022).
Which of the following US macro-economic data releases is most likely to cause Cathie Wood's ARK ETF share price to fall?
Canaccord conducts a sensitivity analysis of the Israeli pharmaceutical firm InterCure's (INCR) estimated share price in figure 33 on page 30:
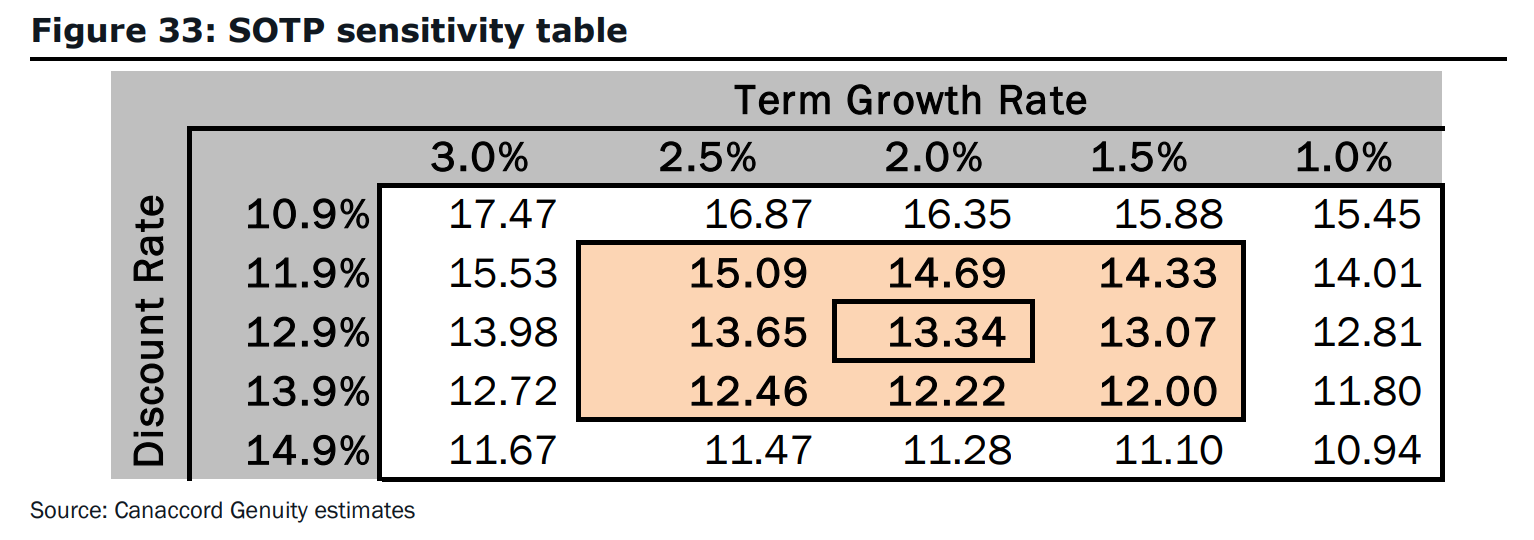
Estimate the Macaulay duration of INCR's equity. The Macaulay duration is approximately:
Question 1070 Multiples valuation, duration, DuPont formula, WACC, mispriced asset
Adam Schwab wrote an article titled 'Why Atlassian is one of the world’s most overvalued businesses' on 15 August 2022. He stated that:
Atlassian is one of the world’s most overvalued businesses by almost any metric. Even though it loses money, Atlassian trades on a multiple of price to sales of a comical 25 times. Stern did a comparison of price-sales multiples in January 2022, noting that the multiple for the entire market was 2.88 and for software (this was before the bubble popped) was 16 times (Schwab, 2022)
Which of the following explanations is NOT correct? Atlassian's stock may be fairly priced if investors beleive that its expected future: