A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
A firm's weighted average cost of capital before tax (##r_\text{WACC before tax}##) would increase due to:
A company has:
- 50 million shares outstanding.
- The market price of one share is currently $6.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts believe that the company's ordinary shares have a beta of 2.
- The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
- The company's debentures are publicly traded and their market price is equal to 90% of their face value.
- The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
A company has:
- 140 million shares outstanding.
- The market price of one share is currently $2.
- The company's debentures are publicly traded and their market price is equal to 93% of the face value.
- The debentures have a total face value of $50,000,000 and the current yield to maturity of corporate debentures is 12% per annum.
- The risk-free rate is 8.50% and the market return is 13.7%.
- Market analysts estimated that the company's stock has a beta of 0.90.
- The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC) in a classical tax system?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of equity to raise money for new projects of similar systematic risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
A company has:
- 10 million common shares outstanding, each trading at a price of $90.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant dividend of 9% of par. They currently trade at a price of $120 each.
- Debentures that have a total face value of $60,000,000 and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 90% of their face value.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts estimate that the company's common stock has a beta of 1.2. The corporate tax rate is 30%.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
A company has:
- 100 million ordinary shares outstanding which are trading at a price of $5 each. Market analysts estimated that the company's ordinary stock has a beta of 1.5. The risk-free rate is 5% and the market return is 10%.
- 1 million preferred shares which have a face (or par) value of $100 and pay a constant annual dividend of 9% of par. The next dividend will be paid in one year. Assume that all preference dividends will be paid when promised. They currently trade at a price of $90 each.
- Debentures that have a total face value of $200 million and a yield to maturity of 6% per annum. They are publicly traded and their market price is equal to 110% of their face value.
The corporate tax rate is 30%. All returns and yields are given as effective annual rates.
What is the company's after-tax Weighted Average Cost of Capital (WACC)? Assume a classical tax system.
Question 237 WACC, Miller and Modigliani, interest tax shield
Which of the following discount rates should be the highest for a levered company? Ignore the costs of financial distress.
Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?
There are many different ways to value a firm's assets. Which of the following will NOT give the correct market value of a levered firm's assets ##(V_L)##? Assume that:
- The firm is financed by listed common stock and vanilla annual fixed coupon bonds, which are both traded in a liquid market.
- The bonds' yield is equal to the coupon rate, so the bonds are issued at par. The yield curve is flat and yields are not expected to change. When bonds mature they will be rolled over by issuing the same number of new bonds with the same expected yield and coupon rate, and so on forever.
- Tax rates on the dividends and capital gains received by investors are equal, and capital gains tax is paid every year, even on unrealised gains regardless of when the asset is sold.
- There is no re-investment of the firm's cash back into the business. All of the firm's excess cash flow is paid out as dividends so real growth is zero.
- The firm operates in a mature industry with zero real growth.
- All cash flows and rates in the below equations are real (not nominal) and are expected to be stable forever. Therefore the perpetuity equation with no growth is suitable for valuation.
Where:
###r_\text{WACC before tax} = r_D.\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital before tax}### ###r_\text{WACC after tax} = r_D.(1-t_c).\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital after tax}### ###NI_L=(Rev-COGS-FC-Depr-\mathbf{IntExp}).(1-t_c) = \text{Net Income Levered}### ###CFFA_L=NI_L+Depr-CapEx - \varDelta NWC+\mathbf{IntExp} = \text{Cash Flow From Assets Levered}### ###NI_U=(Rev-COGS-FC-Depr).(1-t_c) = \text{Net Income Unlevered}### ###CFFA_U=NI_U+Depr-CapEx - \varDelta NWC= \text{Cash Flow From Assets Unlevered}###Question 370 capital budgeting, NPV, interest tax shield, WACC, CFFA
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $600k | |
| Depreciation of equipment per year | $250k | |
| Expected sale price of equipment at end of project | $200k | |
| Revenue per job | $12k | |
| Variable cost per job | $4k | |
| Quantity of jobs per year | 120 | |
| Fixed costs per year, paid at the end of each year | $100k | |
| Interest expense in first year (at t=1) | $16.091k | |
| Interest expense in second year (at t=2) | $9.711k | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Levered cost of equity | 12.5% | |
| Market portfolio return | 10% | |
| Beta of assets | 1.24 | |
| Beta of levered equity | 1.5 | |
| Firm's and project's debt-to-equity ratio | 25% | |
Notes
- The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
- Thousands are represented by 'k' (kilo).
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are nominal. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
A firm plans to issue equity and use the cash raised to pay off its debt. No assets will be bought or sold. Ignore the costs of financial distress.
Which of the following statements is NOT correct, all things remaining equal?
Question 418 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $8m | |
| Depreciation of equipment per year | $8m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 4m | |
| Sale price per unit | $10 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $2m | |
| Interest expense in first year (at t=1) | $0.562m | |
| Corporate tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 9% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.32 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-equity ratio | 50% | |
Notes
- Due to the project, current assets will increase by $6m now (t=0) and fall by $6m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa. All rates are given as effective annual rates.
- The project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Question 419 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM, no explanation
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $6m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 9m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $6 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense in first year (at t=1) | $0.53m | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.08 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-assets ratio | 50% | |
Notes
- Due to the project, current assets will increase by $5m now (t=0) and fall by $5m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-assets ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
One year ago you bought a $1,000,000 house partly funded using a mortgage loan. The loan size was $800,000 and the other $200,000 was your wealth or 'equity' in the house asset.
The interest rate on the home loan was 4% pa.
Over the year, the house produced a net rental yield of 2% pa and a capital gain of 2.5% pa.
Assuming that all cash flows (interest payments and net rental payments) were paid and received at the end of the year, and all rates are given as effective annual rates, what was the total return on your wealth over the past year?
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
You work for XYZ company and you’ve been asked to evaluate a new project which has double the systematic risk of the company’s other projects.
You use the Capital Asset Pricing Model (CAPM) formula and input the treasury yield ##(r_f )##, market risk premium ##(r_m-r_f )## and the company’s asset beta risk factor ##(\beta_{XYZ} )## into the CAPM formula which outputs a return.
This return that you’ve just found is:
Use the below information to value a mature levered company with growing annual perpetual cash flows and a constant debt-to-assets ratio. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. The firm's debt funding comprises annual fixed coupon bonds that all have the same seniority and coupon rate. When these bonds mature, new bonds will be re-issued, and so on in perpetuity. The yield curve is flat.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}_1## | $12.5m | Operating free cash flow at time 1 |
| ##\text{FFCF}_1 \text{ or }\text{CFFA}_1## | $14m | Firm free cash flow or cash flow from assets at time 1 |
| ##\text{EFCF}_1## | $11m | Equity free cash flow at time 1 |
| ##\text{BondCoupons}_1## | $1.2m | Bond coupons paid to debt holders at time 1 |
| ##g## | 2% pa | Growth rate of OFCF, FFCF, EFCF and Debt cash flow |
| ##\text{WACC}_\text{BeforeTax}## | 9% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 8.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Bond yield |
| ##r_\text{EL}## | 13% pa | Cost or required return of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##n_\text{shares}## | 1m | Number of shares |
| ##t_c## | 30% | Corporate tax rate |
Which of the following statements is NOT correct?
Four retail business people compete in the same city. They are all exactly the same except that they have different ways of funding or leasing the shop real estate needed to run their retail business.
The two main assets that retail stores need are:
- Inventory typically worth $1 million which has a beta of 2, and;
- Shopfront real estate worth $1 million which has a beta of 1. Shops can be bought or leased.
Lease contract prices are fixed for the term of the lease and based on expectations of the future state of the economy. When leases end, a new lease contract is negotiated and the lease cost may be higher or lower depending on the state of the economy and demand and supply if the economy is:
- Booming, shop real estate is worth more and lease costs are higher.
- In recession, shop real estate is worth less and lease costs are low.
Which retail business person will have the LOWEST beta of equity (or net wealth)?
An analyst is valuing a levered company whose owners insist on keeping the dollar amount of debt funding fixed. So the company cannot issue or repay its debt, its dollar value must remain constant. Any funding gaps will be met with equity.
The analyst is wondering, as he changes inputs into his valuation, such as the forecast growth rate of sales, then asset values and other things will change. This makes it hard to figure out which values can be held constant and would therefore make good model inputs, rather than outputs which vary depending on the inputs. Assume that the cost of debt (yield) remains constant and the company’s asset beta will also remain constant since any expansion (or downsize) will involve buying (or selling) more of the same assets.
Which of the following values can be assumed to stay constant when projected sales growth increases?
An analyst is valuing a levered company whose owners insist on keeping a constant market debt to assets ratio into the future.
The analyst is wondering how asset values and other things in her model will change when she changes the forecast sales growth rate.
Which of the below values will increase as the forecast growth rate of sales increases, with the debt to assets ratio remaining constant?
Assume that the cost of debt (yield) remains constant and the company’s asset beta will also remain constant since any expansion (or downsize) will involve buying (or selling) more of the same assets.
The analyst should expect which value or ratio to increase when the forecast growth rate of sales increases and the debt to assets ratio remains unchanged? In other words, which of the following values will NOT remain constant?
Meier and Tarhan (2006) conducted an interesting survey of corporate managers. The results are copied in Table 7 below. What proportion of managers are evaluating levered projects correctly?
| Table 7: Consistency between hurdle rate and the calculation of cash flows | |||||||
| Hurdle rate | Cash flow calculation (see below notes) | ||||||
|---|---|---|---|---|---|---|---|
| (i) | (ii) | (iii) | (iv) | (v) | Other | Total | |
| WACC | 11.3% | 34.8% | 1.7% | 3.5% | 18.3% | 1.7% | 71.3% |
| Equity levered | 0.0% | 2.6% | 0.9% | 0.0% | 0.9% | 0.9% | 6.1% |
| Equity unlevered | 1.7% | 1.7% | 0.9% | 0.9% | 1.7% | 0.9% | 7.8% |
| Other | 2.6% | 5.2% | 1.7% | 0.9% | 3.5% | 0.9% | 14.8% |
| Total | 16.5% | 44.4% | 5.2% | 5.2% | 24.4% | 4.4% | 100.0% |
The rows of the cross-tabulation indicate what the self-reported hurdle rate represents and the columns denote five different ways to calculate cash flows, (i) to (v), plus the “other” category. Each cell then displays the fraction of all 113 respondents for a given combination of what the hurdle rate represents and how the firm calculates its cash flows when evaluating a project.
The definitions of the cash flow calculations (i)-(v) are as follows:
(i) Earnings before interest and after taxes (EBIAT) + depreciation
(ii) Earnings before interest and after taxes (EBIAT) + depreciation – capital expenditures – net change in working capital
(iii) Earnings
(iv) Earnings + depreciation
(v) Earnings + depreciation – capital expenditures – net change in working capital
Assume that the WACC is after tax, the required return on unlevered equity is the WACC before tax, all projects are levered, the benefit of interest tax shields should be included in the valuation, earnings = net profit after tax (NPAT) and EBIAT = EBIT*(1-tc) which is often also called net operating profit after tax (NOPAT).
What proportion of managers are evaluating levered projects correctly?
Canaccord conducts a sensitivity analysis of the Israeli pharmaceutical firm InterCure's (INCR) estimated share price in figure 33 on page 30:
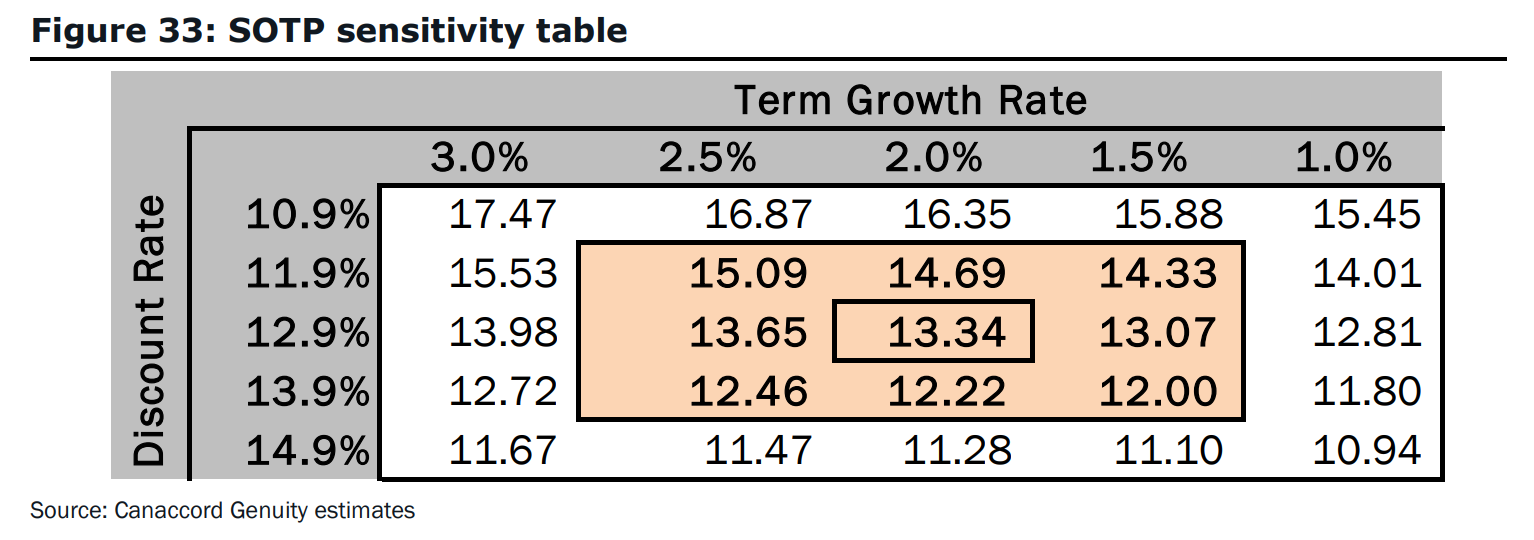
Estimate the Macaulay duration of INCR's equity. The Macaulay duration is approximately:
An analyst has prepared a discounted cash flow model to value a firm's share price. A sensitivity analysis data table with ‘conditional formatting’ shading is shown below. The table shows how changes in the weighted average cost of capital (WACC, left column) and terminal value growth rate (top row) affect the firm's model-estimated share price.
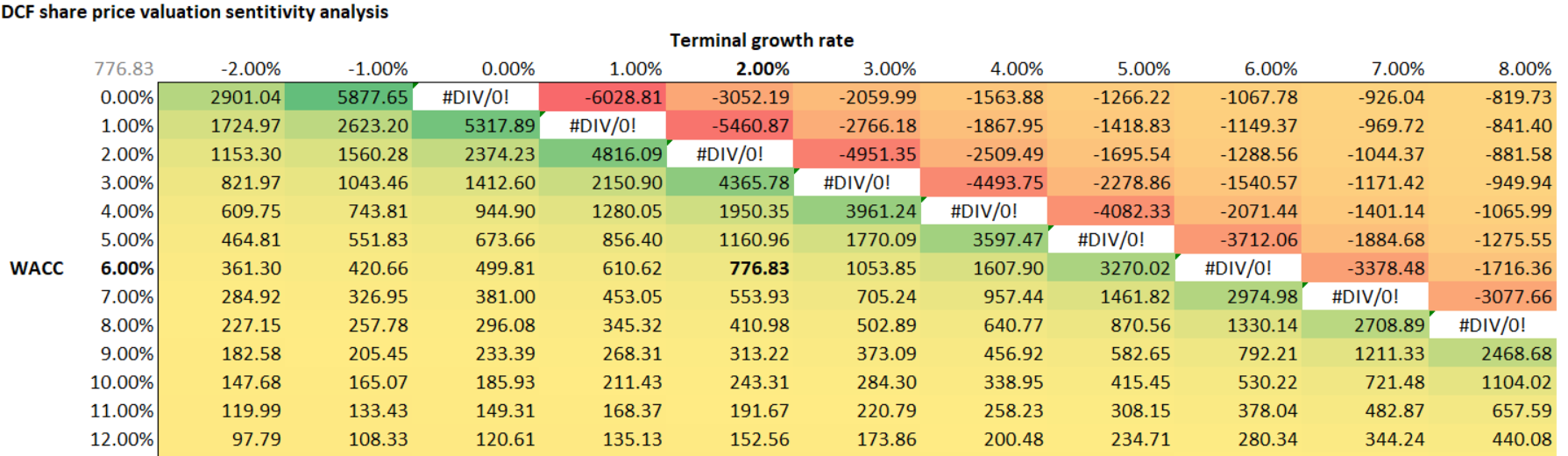
The base case estimates are shown in bold.
Which of the following statements is NOT correct? The model-estimated share price would normally be expected to:
Question 1070 Multiples valuation, duration, DuPont formula, WACC, mispriced asset
Adam Schwab wrote an article titled 'Why Atlassian is one of the world’s most overvalued businesses' on 15 August 2022. He stated that:
Atlassian is one of the world’s most overvalued businesses by almost any metric. Even though it loses money, Atlassian trades on a multiple of price to sales of a comical 25 times. Stern did a comparison of price-sales multiples in January 2022, noting that the multiple for the entire market was 2.88 and for software (this was before the bubble popped) was 16 times (Schwab, 2022)
Which of the following explanations is NOT correct? Atlassian's stock may be fairly priced if investors beleive that its expected future:
A firm is funded with $2 million of loans and $6 million of equity.
The interest rate on the loans is 8% pa. The cost of equity is estimated to be 20% pa. The corporate tax rate is 30% pa.
Which of the below statements is NOT correct? The: