Fight Finance

Question 145  NPV, APR, annuity due

A student just won the lottery. She won $1 million in cash after tax. She is trying to calculate how much she can spend per month for the rest of her life. She assumes that she will live for another 60 years. She wants to withdraw equal amounts at the beginning of every month, starting right now.

All of the cash is currently sitting in a bank account which pays interest at a rate of 6% pa, given as an APR compounding per month. On her last withdrawal, she intends to have nothing left in her bank account. How much can she withdraw at the beginning of each month?

(a) $1,388.89

(b) $5,116.18

(c) $5,141.76

(d) $18,966.13

(e) $19,332.80

Question 244  CAPM, SML, NPV, risk

Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:

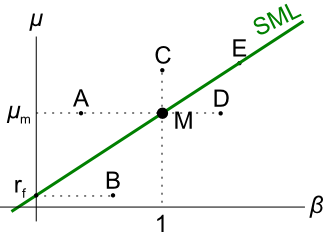
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?

(a) Asset A is underpriced.

(b) Asset B has a negative alpha (a negative excess return or abnormal return).

(c) Buying asset C would be a positive NPV investment.

(d) Asset D has less systematic variance than the market portfolio (M).

(e) Asset E is fairly priced.

Question 272  NPV

Suppose you had $100 in a savings account and the interest rate was 2% per year.

After 5 years, how much do you think you would have in the account if you left the money to grow?

than $102, $102 or than $102?

Question 442  economic depreciation, no explanation

A fairly valued share's current price is $4 and it has a total required return of 30%. Dividends are paid annually and next year's dividend is expected to be $1. After that, dividends are expected to grow by 5% pa. All rates are effective annual returns.

What is the expected dividend cash flow, economic depreciation, and economic income and economic value added (EVA) that will be earned over the second year (from t=1 to t=2) and paid at the end of that year (t=2)?

(a) $1.3, -$0.26, $1.56, $0

(b) $1.25, -$0.25, $1.5, $0

(c) $1.1025, -$0.2205, $1.323, $0

(d) $1.05, -$0.21, $1.26, $0

(e) $1, -$0.2, $1.2, $0

Question 719  mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate

A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.

(a) P1median = $1.105171,   P1mean = $1.521962

(b) P1median = $1.1,             P1mean = $1.42

(c) P1median = $1.521962,   P1mean = $1.105171

(d) P1median = $0.802519,   P1mean = $1.105171

(e) P1median = $1.42,           P1mean = $1.1

Question 776  market efficiency, systematic and idiosyncratic risk, beta, income and capital returns

Which of the following statements about returns is NOT correct? A stock's:

(a) Expected total return will equal its required total return if the stock is fairly priced.

(b) Expected total return will be less than its required total return if the stock is over-priced.

(c) Required total return should be higher than the risk free government bond yield if the stock has a positive beta.

(d) Required total return depends on its total variance, required capital return depends on systematic variance and the dividend yield depends on idiosyncratic variance.

(e) Expected capital return equals the expected total return less whatever the management decide that they will pay as an income return (which is the dividend yield).

Question 779  mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate

Fred owns some BHP shares. He has calculated BHP’s monthly returns for each month in the past 30 years using this formula:

###r_\text{t monthly}=\ln⁡ \left( \dfrac{P_t}{P_{t-1}} \right)###

He then took the arithmetic average and found it to be 0.8% per month using this formula:

###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.008=0.8\% \text{ per month}###

He also found the standard deviation of these monthly returns which was 15% per month:

###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.15=15\%\text{ per month}###

Assume that the past historical average return is the true population average of future expected returns and the stock's returns calculated above ##(r_\text{t monthly})## are normally distributed. Which of the below statements about Fred’s BHP shares is NOT correct?

(a) The returns ##r_\text{t monthly}## are continuously compounded monthly returns.

(b) The mean, median and mode of the continuously compounded annual return is expected to equal 0.8% per month.

(c) The annualised average continuously compounded return is ##\bar{r}_\text{cc annual}=12×0.008=0.096=9.6\%\text{ pa}##. The annualised standard deviation is ##\sigma_\text{annual} = \sqrt{12}×0.15=0.519615242 = 52\%\text{ pa}##.

(d) If the current price of the BHP shares is $20, they're expected to have a median value of $52.2339 ##(= 20×e^{0.008×12×10})## in 10 years.

(e) If the current price of the BHP shares is $20, they're expected to have a mean value of $13.5411 ##(= 20×e^{(0.008 - 0.15^2/2)×12×10})## in 10 years.

Question 901  Basel accord

The below graph from the RBA shows the phase-in of the Basel 3 minimum regulatory capital requirements under the Basel Committee on Banking Supervision (BCBS) on the left panel and in Australia under the Australian Prudential Regulatory Authority (APRA) on the right panel.

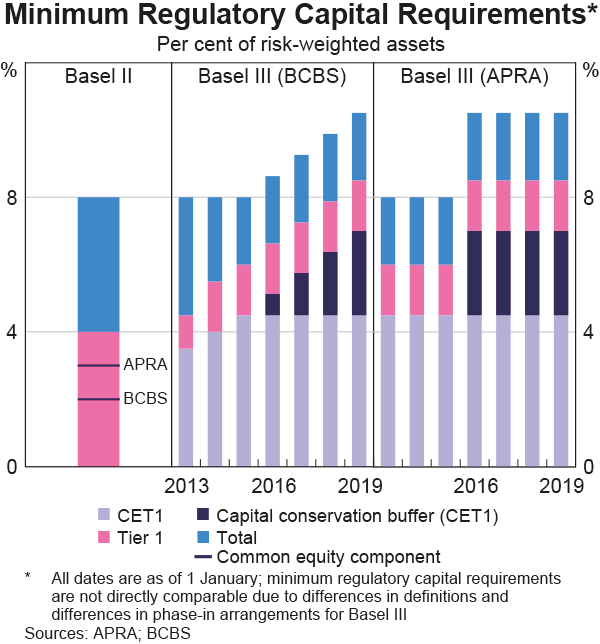
Which of the following statements about the Basel 3 minimum regulatory capital requirements as at 2019 is NOT correct? All minimum amounts exclude the 2.5% counter-cyclical buffer.

The Basel 3 minimum regulatory capital requirement as a percent of Risk Weighted Assets (RWA) is:

(a) 4.5% for Common Equity Tier 1 (CET1).

(b) 2% for Other Tier 1.

(c) 2% for Tier 2.

(d) 8% for overall regulatory capital.

Question 903  option, Black-Scholes-Merton option pricing, option on stock index

A six month European-style call option on the S&P500 stock index has a strike price of 2800 points.

The underlying S&P500 stock index currently trades at 2700 points, has a continuously compounded dividend yield of 2% pa and a standard deviation of continuously compounded returns of 25% pa.

The risk-free interest rate is 5% pa continuously compounded.

Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:

(a) 162.83 points

(b) 220.56 points

(c) 226.43 points

(d) 230.91 points

(e) 317.45 points

Question 965  foreign exchange reserve, foreign exchange rate, no explanation

Observe the below graph of Chinese foreign exchange reserves held by the central bank, as well as the Chinese currency the Yuan (CNY, also called the Renminbi, RMB) against the US Dollar. Note the inverted y-axis scale on the Yuan exchange rate graph.

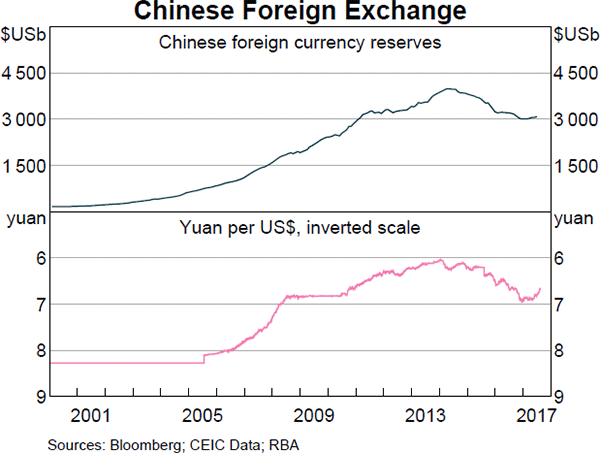
Which of the below statements is NOT correct?

(a) To increase FX reserves the Chinese central bank must buy CNY.

(b) The CNY appreciated against the USD from 2005 to 2013.

(c) The CNY was fixed prior to 2005 and from 2008 to 2010.

(d) If the Chinese central bank buys CNY using USD, the CNY is likely to appreciate against the USD, all other things remaining equal.

(e) The Chinese central bank spent its FX reserves from 2014 to 2016.