A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as a fully amortising loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.
What will be your monthly payments? Remember that mortgage loan payments are paid in arrears (at the end of the month).
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
You really want to go on a back packing trip to Europe when you finish university. Currently you have $1,500 in the bank. Bank interest rates are 8% pa, given as an APR compounding per month. If the holiday will cost $2,000, how long will it take for your bank account to reach that amount?
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Question 64 inflation, real and nominal returns and cash flows, APR, effective rate
In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.
The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
Your credit card shows a $600 debt liability. The interest rate is 24% pa, payable monthly. You can't pay any of the debt off, except in 6 months when it's your birthday and you'll receive $50 which you'll use to pay off the credit card. If that is your only repayment, how much will the credit card debt liability be one year from now?
You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.
How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.
A student just won the lottery. She won $1 million in cash after tax. She is trying to calculate how much she can spend per month for the rest of her life. She assumes that she will live for another 60 years. She wants to withdraw equal amounts at the beginning of every month, starting right now.
All of the cash is currently sitting in a bank account which pays interest at a rate of 6% pa, given as an APR compounding per month. On her last withdrawal, she intends to have nothing left in her bank account. How much can she withdraw at the beginning of each month?
A three year corporate bond yields 12% pa with a coupon rate of 10% pa, paid semi-annually.
Find the effective six month yield, effective annual yield and the effective daily yield. Assume that each month has 30 days and that there are 360 days in a year.
All answers are given in the same order:
##r_\text{eff semi-annual}##, ##r_\text{eff yearly}##, ##r_\text{eff daily}##.
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
A 2 year government bond yields 5% pa with a coupon rate of 6% pa, paid semi-annually.
Find the effective six month rate, effective annual rate and the effective daily rate. Assume that each month has 30 days and that there are 360 days in a year.
All answers are given in the same order:
##r_\text{eff semi-annual}##, ##r_\text{eff yrly}##, ##r_\text{eff daily}##.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
Harvey Norman the large retailer often runs sales advertising 2 years interest free when you purchase its products. This offer can be seen as a free personal loan from Harvey Norman to its customers.
Assume that banks charge an interest rate on personal loans of 12% pa given as an APR compounding per month. This is the interest rate that Harvey Norman deserves on the 2 year loan it extends to its customers. Therefore Harvey Norman must implicitly include the cost of this loan in the advertised sale price of its goods.
If you were a customer buying from Harvey Norman, and you were paying immediately, not in 2 years, what is the minimum percentage discount to the advertised sale price that you would insist on? (Hint: if it makes it easier, assume that you’re buying a product with an advertised price of $100).
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
To your surprise, you can actually afford to pay $2,000 per month and your mortgage allows early repayments without fees. If you maintain these higher monthly payments, how long will it take to pay off your mortgage?
You just agreed to a 30 year fully amortising mortgage loan with monthly payments of $2,500. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change. The below choices are given in the same order.
You just started work at your new job which pays $48,000 per year.
The human resources department have given you the option of being paid at the end of every week or every month.
Assume that there are 4 weeks per month, 12 months per year and 48 weeks per year.
Bank interest rates are 12% pa given as an APR compounding per month.
What is the dollar gain over one year, as a net present value, of being paid every week rather than every month?
Your main expense is fuel for your car which costs $100 per month. You just refueled, so you won't need any more fuel for another month (first payment at t=1 month).
You have $2,500 in a bank account which pays interest at a rate of 6% pa, payable monthly. Interest rates are not expected to change.
Assuming that you have no income, in how many months time will you not have enough money to fully refuel your car?
A 2 year corporate bond yields 3% pa with a coupon rate of 5% pa, paid semi-annually.
Find the effective monthly rate, effective six month rate, and effective annual rate.
##r_\text{eff monthly}##, ##r_\text{eff 6 month}##, ##r_\text{eff annual}##.
You want to buy a house priced at $400,000. You have saved a deposit of $40,000. The bank has agreed to lend you $360,000 as a fully amortising loan with a term of 30 years. The interest rate is 8% pa payable monthly and is not expected to change.
What will be your monthly payments?
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
You're trying to save enough money for a deposit to buy a house. You want to buy a house worth $400,000 and the bank requires a 20% deposit ($80,000) before it will give you a loan for the other $320,000 that you need.
You currently have no savings, but you just started working and can save $2,000 per month, with the first payment in one month from now. Bank interest rates on savings accounts are 4.8% pa with interest paid monthly and interest rates are not expected to change.
How long will it take to save the $80,000 deposit? Round your answer up to the nearest month.
A student won $1m in a lottery. Currently the money is in a bank account which pays interest at 6% pa, given as an APR compounding per month.
She plans to spend $20,000 at the beginning of every month from now on (so the first withdrawal will be at t=0). After each withdrawal, she will check how much money is left in the account. When there is less than $500,000 left, she will donate that remaining amount to charity.
In how many months will she make her last withdrawal and donate the remainder to charity?
Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
A 10 year Australian government bond was just issued at par with a yield of 3.9% pa. The fixed coupon payments are semi-annual. The bond has a face value of $1,000.
Six months later, just after the first coupon is paid, the yield of the bond decreases to 3.65% pa. What is the bond's new price?
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which one of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Many Australian home loans that are interest-only actually require payments to be made on a fully amortising basis after a number of years.
You decide to borrow $600,000 from the bank at an interest rate of 4.25% pa for 25 years. The payments will be interest-only for the first 10 years (t=0 to 10 years), then they will have to be paid on a fully amortising basis for the last 15 years (t=10 to 25 years).
Assuming that interest rates will remain constant, what will be your monthly payments over the first 10 years from now, and then the next 15 years after that? The answer options are given in the same order.
You just entered into a fully amortising home loan with a principal of $600,000, a variable interest rate of 4.25% pa and a term of 25 years.
Immediately after settling the loan, the variable interest rate suddenly falls to 4% pa! You can't believe your luck. Despite this, you plan to continue paying the same home loan payments as you did before. How long will it now take to pay off your home loan?
Assume that the lower interest rate was granted immediately and that rates were and are now again expected to remain constant. Round your answer up to the nearest whole month.
A home loan company advertises an interest rate of 6% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A credit card company advertises an interest rate of 18% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A semi-annual coupon bond has a yield of 3% pa. Which of the following statements about the yield is NOT correct? All rates are given to four decimal places.
Question 659 APR, effective rate, effective rate conversion, no explanation
A home loan company advertises an interest rate of 9% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given with an accuracy of 4 decimal places.
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###Question 662 APR, effective rate, effective rate conversion, no explanation
Which of the following interest rate labels does NOT make sense?
Which of the following interest rate quotes is NOT equivalent to a 10% effective annual rate of return? Assume that each year has 12 months, each month has 30 days, each day has 24 hours, each hour has 60 minutes and each minute has 60 seconds. APR stands for Annualised Percentage Rate.
A home loan company advertises an interest rate of 4.5% pa, payable monthly. Which of the following statements about the interest rate is NOT correct?
You just spent $1,000 on your credit card. The interest rate is 24% pa compounding monthly. Assume that your credit card account has no fees and no minimum monthly repayment.
If you can't make any interest or principal payments on your credit card debt over the next year, how much will you owe one year from now?
Below is a screenshot from ASIC’s MoneySmart future value compound interest calculator website.
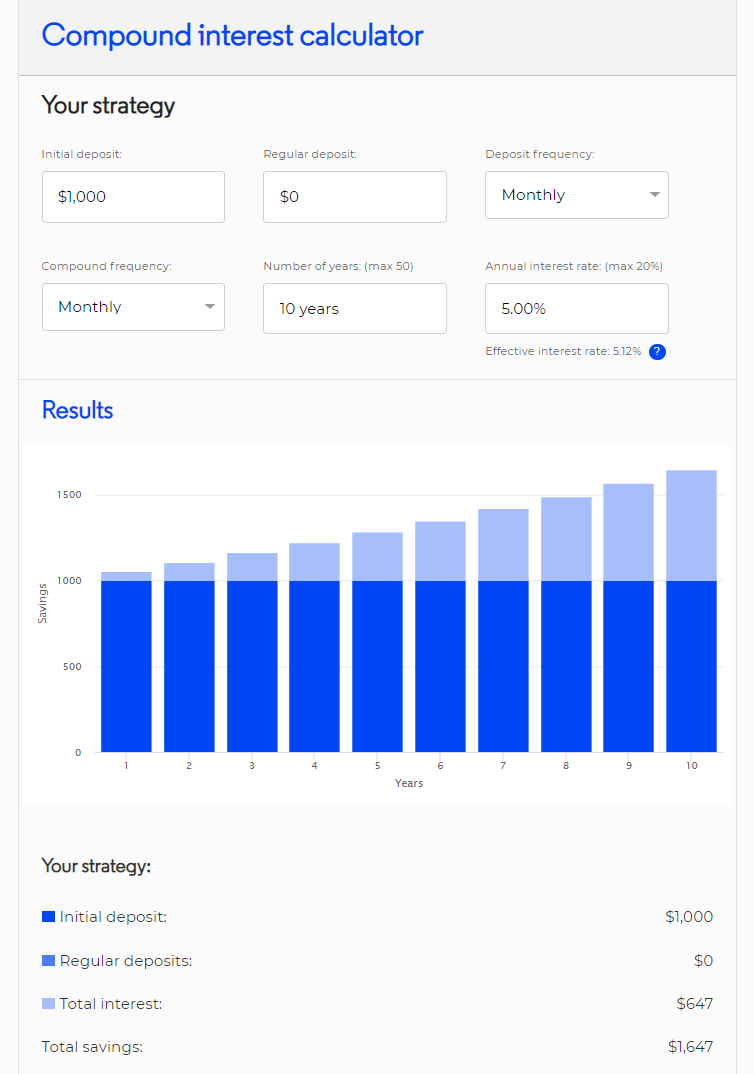
It shows that $1,000 invested in a bank account at 5% pa compounding monthly for 10 years will be worth $1,647, rounded to the nearest dollar.
Which of the following formulas replicates this result?
Below is a screenshot from ASIC’s MoneySmart future value compound interest calculator website.
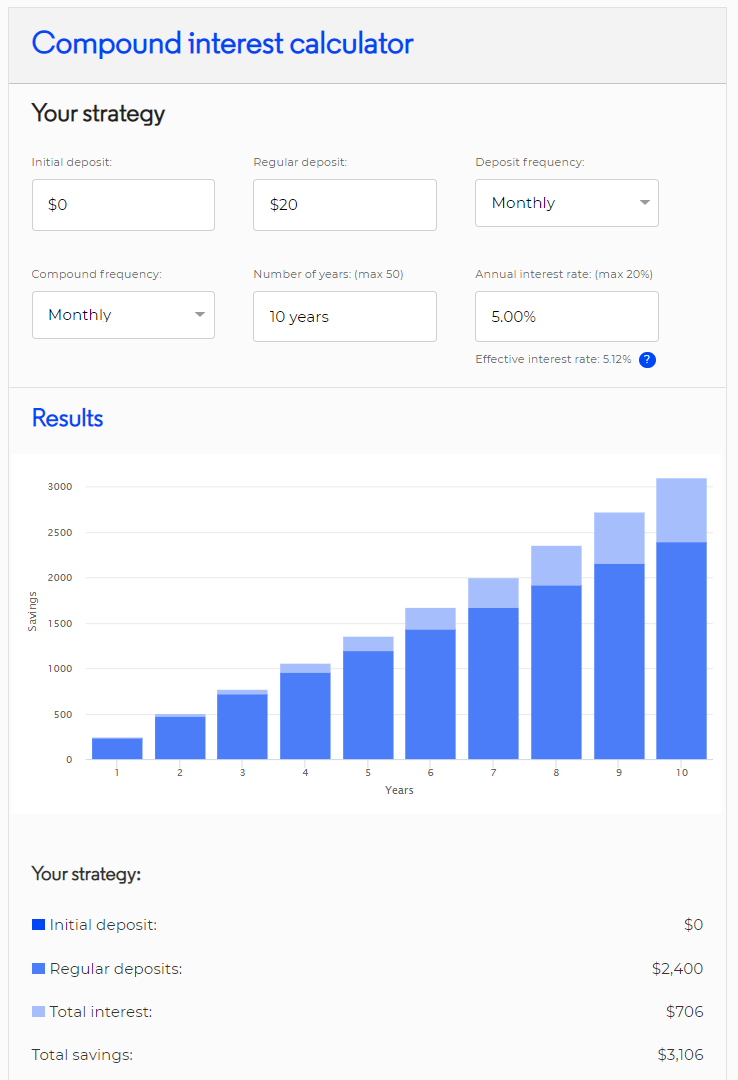
It shows that $20 invested (or deposited) into a bank account at the end of every month for 10 years at 5% pa compounding monthly will be worth $3,106 at the end of the 10 years, rounded to the nearest dollar.
Which of the following formulas replicates this result?
You wish to borrow $2,500 for 2 years to start a business. You approach different lenders who have the following offers. Which is the best lender to borrow from? All percentage rates are rounded to 6 decimal places.
Question 1076 fully amortising loan, interest only loan, APR
You just borrowed $800,000 using a 25 year home loan that's interest-only for the first 2 years, and principal and interest (P&I) for the remaining 23 years.
The interest rate is 7.44% pa compounding monthly which is not expected to change.
Which of the following statements is NOT correct?