Fight Finance

Question 4  DDM

For a price of $13, Carla will sell you a share paying a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.

Would you like to Carla's share or politely ?

Question 65  annuity with growth, needs refinement

Which of the below formulas gives the present value of an annuity with growth?

(a) ##\dfrac{C_1}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

(b) ##\dfrac{C_1(1+g)^T}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

(c) ##\dfrac{C_1}{r-g}\left(1-\dfrac{1+g}{(1+r)^T}\right)##

(d) ##\dfrac{C_1}{r-g}\left(1-\left(\dfrac{1+g}{1+r}\right)^T \right)##

(e) ##\dfrac{C_1(1+g)}{r-g}\left(1-\dfrac{1}{(1+r)^T}\right)##

Hint: The equation of a perpetuity without growth is: ###V_\text{0, perp without growth} = \frac{C_\text{1}}{r}###

The formula for the present value of an annuity without growth is derived from the formula for a perpetuity without growth.

The idea is than an annuity with T payments from t=1 to T inclusive is equivalent to a perpetuity starting at t=1 with fixed positive cash flows, plus a perpetuity starting T periods later (t=T+1) with fixed negative cash flows. The positive and negative cash flows after time period T cancel each other out, leaving the positive cash flows between t=1 to T, which is the annuity.

###\begin{aligned} V_\text{0, annuity} &= V_\text{0, perp without growth from t=1} - V_\text{0, perp without growth from t=T+1} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{T+1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r} - \dfrac{ \left( \dfrac{C_\text{1}}{r} \right) }{(1+r)^T} \\ &= \dfrac{C_\text{1}}{r}\left(1 - \dfrac{1}{(1+r)^T}\right) \\ \end{aligned}###

The equation of a perpetuity with growth is:

###V_\text{0, perp with growth} = \dfrac{C_\text{1}}{r-g}###

Question 255  bond pricing

In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.

A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?

(a) 94.20452353

(b) 100

(c) 106

(d) 112

(e) The bond is priceless.

Question 375  interest tax shield, CFFA

One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use net operating profit after tax (NOPAT).

###\begin{aligned} FFCF &= NOPAT + Depr - CapEx -\Delta NWC \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC \\ \end{aligned} \\###

Does this annual FFCF or the annual interest tax shield?

Question 406  leverage, WACC, margin loan, portfolio return

One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.

The interest rate on the margin loan was 7.84% pa.

Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.

What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.

(a) 1.0757%

(b) 2.7067%

(c) 5.1333%

(d) 9.0000%

(e) 11.7067%

Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).

Question 688  future, hedging

A pig farmer in the US is worried about the price of hogs falling and wants to lock in a price now. In one year the pig farmer intends to sell 1,000,000 pounds of hogs. Luckily, one year CME lean hog futures expire on the exact day that he wishes to sell his pigs. The futures have a notional principal of 40,000 pounds (about 18 metric tons) and currently trade at a price of 63.85 cents per pound. The underlying lean hogs spot price is 77.15 cents per pound. The correlation between the futures price and the underlying hogs price is one and the standard deviations are both 4 cents per pound. The initial margin is USD1,500 and the maintenance margin is USD1,200 per futures contract.

Which of the below statements is NOT correct?

(a) The pig farmer should sell futures to hedge against the danger of falling hog prices.

(b) The pig farmer should transact 30 lean hogs futures contracts with tailing since futures contracts require margins.

(c) The total initial margin that must be paid to the pig farmer’s futures broker is $45,000.

(d) If the futures price falls by more than 0.01175 cents per pound (rounded to 5 decimal places) then the pig farmer will receive a margin call from their broker.

(e) The future is trading in backwardation since the spot price exceeds the futures price, so the current basis is positive 13.30 cents.

Question 723  mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate

Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?

Price and Return Population Statistics
Time	Prices	LGDR	GDR	NDR
0	100
1	99	-0.010050	0.990000	-0.010000
2	180.40	0.600057	1.822222	0.822222
3	112.73	0.470181	0.624889	0.375111
Arithmetic average		0.0399	1.1457	0.1457
Arithmetic standard deviation		0.4384	0.5011	0.5011

 

(a) The geometric average of the gross discrete returns (GAGDR) equals 1.04075 which is 104.075%.

(b) ##\exp \left( \text{GAGDR} \right) = \text{AALGDR}##. The natural exponent of the GAGDR equals the arithmetic average of the logarithms of the gross discrete returns (AALGDR).

(c) ##\text{GAGDR}^T = \left( P_T/P_0 \right)##. The GAGDR raised to the power of the number of time period that it's measured over equals the ratio of the first and last prices.

(d) ##\text{GAGDR} = \exp \left( \text{AALGDR} \right)##. This is always true, regardless of the distribution of the prices or returns. The logarithm of the geometric average of the gross discrete returns (LGAGDR) is always equal to the arithmetic average of the logarithm of the gross discrete returns (AALGDR).

(e) ##\text{AAGDR} \approx \exp \left( \text{AALGDR} + \text{SDLGDR}^2/2 \right)##. This is only approximately true and depends on the distribution of the prices and returns. It's asymptotically true as the time period that the returns are measured over reaches infinity.

Question 824  option, no explanation

A put option written on a risky non-dividend paying stock will mature in one month. As is normal, assume that the option's exercise price is non-zero and positive ##(K>0)## and the stock has limited liability ##(S>0)##.

Which of the following statements is NOT correct? The put option's:

(a) Price must be greater than zero (p>0).

(b) Price can be greater than its exercise price (p>K).

(c) Price can be greater than the underlying asset's price (p>S).

(d) Exercise price can be greater than the underlying asset's price (K>S).

(e) Profit must be less than the payoff at maturity from the long trader’s perspective.

Question 826  future, basis risk, hedging

On 1 February 2016 you were told that your refinery company will need to purchase oil on 1 July 2016. You were afraid of the oil price rising between now and then so you bought some August 2016 futures contracts on 1 February 2016 to hedge against changes in the oil price. On 1 February 2016 the oil price was $40 and the August 2016 futures price was $43.

It's now 1 July 2016 and oil price is $45 and the August 2016 futures price is $46. You bought the spot oil and closed out your futures position on 1 July 2016.

What was the effective price paid for the oil, taking into account basis risk? All spot and futures oil prices quoted above and below are per barrel.

(a) $37

(b) $42

(c) $44

(d) $45

(e) $48

Question 892  foreign exchange reserve, foreign exchange rate, no explanation

The Chinese central bank has the largest amount of foreign currency reserves.

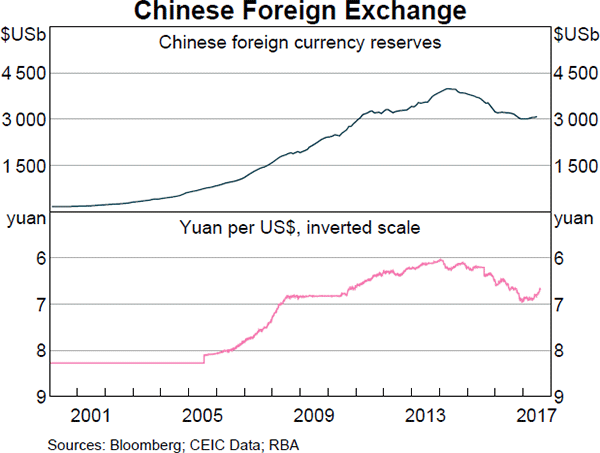
What could the large amounts of foreign exchange reserves held by the Chinese government be used for in a currency crisis? China's currency is called the Renminbi (RMB) or Yuan (CNY). In a Chinese currency crisis the Chinese government is likely to use its FX reserves to:

(a) Buy RMB.

(b) Buy USD.

(c) Buy EUR.

(d) Buy JPY.

(e) Sell RMB.