Question 448 franking credit, personal tax on dividends, imputation tax system
A small private company has a single shareholder. This year the firm earned a $100 profit before tax. All of the firm's after tax profits will be paid out as dividends to the owner.
The corporate tax rate is 30% and the sole shareholder's personal marginal tax rate is 45%.
The Australian imputation tax system applies because the company generates all of its income in Australia and pays corporate tax to the Australian Tax Office. Therefore all of the company's dividends are fully franked. The sole shareholder is an Australian for tax purposes and can therefore use the franking credits to offset his personal income tax liability.
What will be the personal tax payable by the shareholder and the corporate tax payable by the company?
Question 624 franking credit, personal tax on dividends, imputation tax system, no explanation
Which of the following statements about Australian franking credits is NOT correct? Franking credits:
The expression 'you have to spend money to make money' relates to which business decision?
Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Question 539 debt terminology, fully amortising loan, bond pricing
A 'fully amortising' loan can also be called a:
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
A home loan company advertises an interest rate of 6% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A semi-annual coupon bond has a yield of 3% pa. Which of the following statements about the yield is NOT correct? All rates are given to four decimal places.
A prospective home buyer can afford to pay $2,000 per month in mortgage loan repayments. The central bank recently lowered its policy rate by 0.25%, and residential home lenders cut their mortgage loan rates from 4.74% to 4.49%.
How much more can the prospective home buyer borrow now that interest rates are 4.49% rather than 4.74%? Give your answer as a proportional increase over the original amount he could borrow (##V_\text{before}##), so:
###\text{Proportional increase} = \frac{V_\text{after}-V_\text{before}}{V_\text{before}} ###Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates compounding per month.
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 3 years from now (first payment at t=3).
- 1 payment of $600 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
You are promised 20 payments of $100, where the first payment is immediate (t=0) and the last is at the end of the 19th year (t=19). The effective annual discount rate is ##r##.
Which of the following equations does NOT give the correct present value of these 20 payments?
Some countries' interest rates are so low that they're zero.
If interest rates are 0% pa and are expected to stay at that level for the foreseeable future, what is the most that you would be prepared to pay a bank now if it offered to pay you $10 at the end of every year for the next 5 years?
In other words, what is the present value of five $10 payments at time 1, 2, 3, 4 and 5 if interest rates are 0% pa?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
You're considering a business project which costs $11m now and is expected to pay a single cash flow of $11m in one year. So you pay $11m now, then one year later you receive $11m.
Assume that the initial $11m cost is funded using the your firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about the net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
A pharmaceutical firm has just discovered a valuable new drug. So far the news has been kept a secret.
The net present value of making and commercialising the drug is $200 million, but $600 million of bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and bond raising to shareholders simultaneously in the same announcement. The bonds will be issued shortly after.
Once the announcement is made and the bonds are issued, what is the expected increase in the value of the firm's assets (ΔV), market capitalisation of debt (ΔD) and market cap of equity (ΔE)?
The triangle symbol is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##ΔV = ΔD+ΔE##
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.
So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.
The required return of the stock is 15% pa.
The following is the Dividend Discount Model (DDM) used to price stocks:
###P_0=\dfrac{C_1}{r-g}###
If the assumptions of the DDM hold and the stock is fairly priced, which one of the following statements is NOT correct? The long term expected:
Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
A stock is expected to pay its first dividend of $20 in 3 years (t=3), which it will continue to pay for the next nine years, so there will be ten $20 payments altogether with the last payment in year 12 (t=12).
From the thirteenth year onward, the dividend is expected to be 4% more than the previous year, forever. So the dividend in the thirteenth year (t=13) will be $20.80, then $21.632 in year 14, and so on forever. The required return of the stock is 10% pa. All rates are effective annual rates. Calculate the current (t=0) stock price.
A stock is expected to pay a dividend of $15 in one year (t=1), then $25 for 9 years after that (payments at t=2 ,3,...10), and on the 11th year (t=11) the dividend will be 2% less than at t=10, and will continue to shrink at the same rate every year after that forever. The required return of the stock is 10%. All rates are effective annual rates.
What is the price of the stock now?
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid semi-annually. So there are two coupons per year, paid in arrears every six months.
For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.
An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
The following table shows a sample of historical total returns of shares in two different companies A and B.
| Stock Returns | ||
| Total effective annual returns | ||
| Year | ##r_A## | ##r_B## |
| 2007 | 0.2 | 0.4 |
| 2008 | 0.04 | -0.2 |
| 2009 | -0.1 | -0.3 |
| 2010 | 0.18 | 0.5 |
What is the historical sample covariance (##\hat{\sigma}_{A,B}##) and correlation (##\rho_{A,B}##) of stock A and B's total effective annual returns?
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
What is the covariance of a variable X with itself?
The cov(X, X) or ##\sigma_{X,X}## equals:
A stock's returns are normally distributed with a mean of 10% pa and a standard deviation of 20 percentage points pa. What is the 95% confidence interval of returns over the next year? Note that the Z-statistic corresponding to a one-tail:
- 90% normal probability density function is 1.282.
- 95% normal probability density function is 1.645.
- 97.5% normal probability density function is 1.960.
The 95% confidence interval of annual returns is between:
A firm can issue 5 year annual coupon bonds at a yield of 8% pa and a coupon rate of 12% pa.
The beta of its levered equity is 1. Five year government bonds yield 5% pa with a coupon rate of 6% pa. The market's expected dividend return is 4% pa and its expected capital return is 6% pa.
The firm's debt-to-equity ratio is 2:1. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?
You may assume:
- the value of debt (D) is constant through time,
- The cost of debt and the yield on debt are equal and given by ##r_D##.
- the appropriate rate to discount interest tax shields is ##r_D##.
- ##\text{IntExp}=D.r_D##
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Question 772 interest tax shield, capital structure, leverage
A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?
A company conducts a 4 for 3 stock split. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order.
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Which firms tend to have high forward-looking price-earnings (PE) ratios?
Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
Question 809 Markowitz portfolio theory, CAPM, Jensens alpha, CML, systematic and idiosyncratic risk
A graph of assets’ expected returns ##(\mu)## versus standard deviations ##(\sigma)## is given in the graph below. The CML is the capital market line.
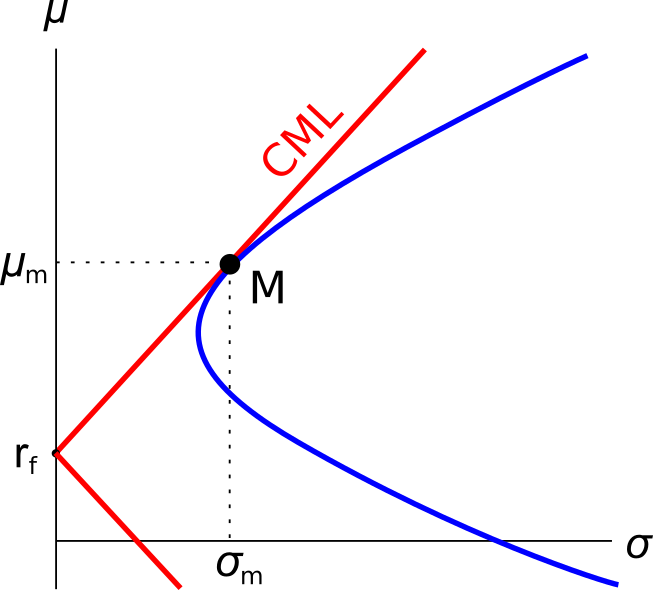
Which of the following statements about this graph, Markowitz portfolio theory and the Capital Asset Pricing Model (CAPM) theory is NOT correct?
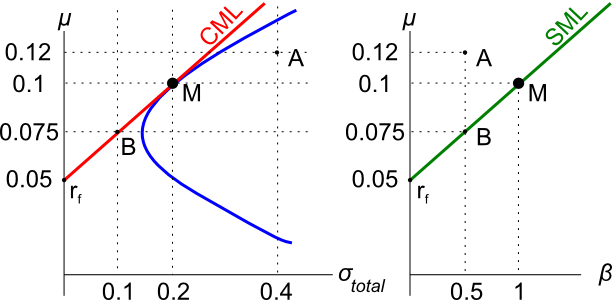
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
Question 780 mispriced asset, NPV, DDM, market efficiency, no explanation
A company advertises an investment costing $1,000 which they say is under priced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Of the 15% pa total expected return, the dividend yield is expected to be 4% pa and the capital yield 11% pa. Assume that the company's statements are correct.
What is the NPV of buying the investment if the 15% total return lasts for the next 100 years (t=0 to 100), then reverts to 10% after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant, the dividends can only be re-invested at 10% pa and all returns are given as effective annual rates. The answer choices below are given in the same order (15% for 100 years, and 15% forever):