Question 542 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to double every 10 years, what must be the expected future capital return, given as an effective annual rate?
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 295 inflation, real and nominal returns and cash flows, NPV
When valuing assets using discounted cash flow (net present value) methods, it is important to consider inflation. To properly deal with inflation:
(I) Discount nominal cash flows by nominal discount rates.
(II) Discount nominal cash flows by real discount rates.
(III) Discount real cash flows by nominal discount rates.
(IV) Discount real cash flows by real discount rates.
Which of the above statements is or are correct?
Question 575 inflation, real and nominal returns and cash flows
You expect a nominal payment of $100 in 5 years. The real discount rate is 10% pa and the inflation rate is 3% pa. Which of the following statements is NOT correct?
Question 554 inflation, real and nominal returns and cash flows
On his 20th birthday, a man makes a resolution. He will put $30 cash under his bed at the end of every month starting from today. His birthday today is the first day of the month. So the first addition to his cash stash will be in one month. He will write in his will that when he dies the cash under the bed should be given to charity.
If the man lives for another 60 years, how much money will be under his bed if he dies just after making his last (720th) addition?
Also, what will be the real value of that cash in today's prices if inflation is expected to 2.5% pa? Assume that the inflation rate is an effective annual rate and is not expected to change.
The answers are given in the same order, the amount of money under his bed in 60 years, and the real value of that money in today's prices.
Question 745 real and nominal returns and cash flows, inflation, income and capital returns
If the nominal gold price is expected to increase at the same rate as inflation which is 3% pa, which of the following statements is NOT correct?
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
The expression 'you have to spend money to make money' relates to which business decision?
Some countries' interest rates are so low that they're zero.
If interest rates are 0% pa and are expected to stay at that level for the foreseeable future, what is the most that you would be prepared to pay a bank now if it offered to pay you $10 at the end of every year for the next 5 years?
In other words, what is the present value of five $10 payments at time 1, 2, 3, 4 and 5 if interest rates are 0% pa?
Discounted cash flow (DCF) valuation prices assets by finding the present value of the asset's future cash flows. The single cash flow, annuity, and perpetuity equations are very useful for this.
Which of the following equations is the 'perpetuity with growth' equation?
A stock is just about to pay a dividend of $1 tonight. Future annual dividends are expected to grow by 2% pa. The next dividend of $1 will be paid tonight, and the year after that the dividend will be $1.02 (=1*(1+0.02)^1), and a year later 1.0404 (=1*(1+0.04)^2) and so on forever.
Its required total return is 10% pa. The total required return and growth rate of dividends are given as effective annual rates.
Calculate the current stock price.
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

The following cash flows are expected:
- 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
- 1 payment of $400 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
The following is the Dividend Discount Model (DDM) used to price stocks:
###P_0=\dfrac{C_1}{r-g}###
If the assumptions of the DDM hold and the stock is fairly priced, which one of the following statements is NOT correct? The long term expected:
A stock just paid its annual dividend of $9. The share price is $60. The required return of the stock is 10% pa as an effective annual rate.
What is the implied growth rate of the dividend per year?
Question 497 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
A stock is expected to pay a dividend of $15 in one year (t=1), then $25 for 9 years after that (payments at t=2 ,3,...10), and on the 11th year (t=11) the dividend will be 2% less than at t=10, and will continue to shrink at the same rate every year after that forever. The required return of the stock is 10%. All rates are effective annual rates.
What is the price of the stock now?
Question 31 DDM, perpetuity with growth, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?
The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in three and a half years (t = 3.5)?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_0 = \frac{d_1}{r - g} ###
Which expression is NOT equal to the expected dividend yield?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###p_0=\frac{d_1}{r_\text{eff}-g_\text{eff}}###
Which expression is NOT equal to the expected capital return?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
The boss of WorkingForTheManCorp has a wicked (and unethical) idea. He plans to pay his poor workers one week late so that he can get more interest on his cash in the bank.
Every week he is supposed to pay his 1,000 employees $1,000 each. So $1 million is paid to employees every week.
The boss was just about to pay his employees today, until he thought of this idea so he will actually pay them one week (7 days) later for the work they did last week and every week in the future, forever.
Bank interest rates are 10% pa, given as a real effective annual rate. So ##r_\text{eff annual, real} = 0.1## and the real effective weekly rate is therefore ##r_\text{eff weekly, real} = (1+0.1)^{1/52}-1 = 0.001834569##
All rates and cash flows are real, the inflation rate is 3% pa and there are 52 weeks per year. The boss will always pay wages one week late. The business will operate forever with constant real wages and the same number of employees.
What is the net present value (NPV) of the boss's decision to pay later?
Question 727 inflation, real and nominal returns and cash flows
The Australian Federal Government lends money to domestic students to pay for their university education. This is known as the Higher Education Contribution Scheme (HECS). The nominal interest rate on the HECS loan is set equal to the consumer price index (CPI) inflation rate. The interest is capitalised every year, which means that the interest is added to the principal. The interest and principal does not need to be repaid by students until they finish study and begin working.
Which of the following statements about HECS loans is NOT correct?
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
A share currently worth $100 is expected to pay a constant dividend of $4 for the next 5 years with the first dividend in one year (t=1) and the last in 5 years (t=5).
The total required return is 10% pa.
What do you expected the share price to be in 5 years, just after the dividend at that time has been paid?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0), in one year (t=1) and in two years (t=2), and still have $50,000 in the bank after that (t=2).
How much can you consume at each time?
What is the net present value (NPV) of undertaking a full-time Australian undergraduate business degree as an Australian citizen? Only include the cash flows over the duration of the degree, ignore any benefits or costs of the degree after it's completed.
Assume the following:
- The degree takes 3 years to complete and all students pass all subjects.
- There are 2 semesters per year and 4 subjects per semester.
- University fees per subject per semester are $1,277, paid at the start of each semester. Fees are expected to remain constant in real terms for the next 3 years.
- There are 52 weeks per year.
- The first semester is just about to start (t=0). The first semester lasts for 19 weeks (t=0 to 19).
- The second semester starts immediately afterwards (t=19) and lasts for another 19 weeks (t=19 to 38).
- The summer holidays begin after the second semester ends and last for 14 weeks (t=38 to 52). Then the first semester begins the next year, and so on.
- Working full time at the grocery store instead of studying full-time pays $20/hr and you can work 35 hours per week. Wages are paid at the end of each week and are expected to remain constant in real terms.
- Full-time students can work full-time during the summer holiday at the grocery store for the same rate of $20/hr for 35 hours per week.
- The discount rate is 9.8% pa. All rates and cash flows are real. Inflation is expected to be 3% pa. All rates are effective annual.
The NPV of costs from undertaking the university degree is:
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
Find Candys Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Candys Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 50 | |
| Operating expense | 10 | |
| Depreciation | 20 | |
| Interest expense | 10 | |
| Income before tax | 110 | |
| Tax at 30% | 33 | |
| Net income | 77 | |
| Candys Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 220 | 180 |
| PPE | ||
| Cost | 300 | 340 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 240 | 300 |
| Total assets | 460 | 480 |
| Liabilities | ||
| Current liabilities | 175 | 190 |
| Non-current liabilities | 135 | 130 |
| Owners' equity | ||
| Retained earnings | 50 | 60 |
| Contributed equity | 100 | 100 |
| Total L and OE | 460 | 480 |
Note: all figures are given in millions of dollars ($m).
Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Sidebar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 405 | |
| COGS | 100 | |
| Depreciation | 34 | |
| Rent expense | 22 | |
| Interest expense | 39 | |
| Taxable Income | 210 | |
| Taxes at 30% | 63 | |
| Net income | 147 | |
| Sidebar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Cash | 0 | 0 |
| Inventory | 70 | 50 |
| Trade debtors | 11 | 16 |
| Rent paid in advance | 4 | 3 |
| PPE | 700 | 680 |
| Total assets | 785 | 749 |
| Trade creditors | 11 | 19 |
| Bond liabilities | 400 | 390 |
| Contributed equity | 220 | 220 |
| Retained profits | 154 | 120 |
| Total L and OE | 785 | 749 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| World Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 300 | |
| COGS | 150 | |
| Operating expense | 50 | |
| Depreciation | 40 | |
| Interest expense | 10 | |
| Taxable income | 50 | |
| Tax at 30% | 15 | |
| Net income | 35 | |
| World Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 200 | 230 |
| PPE | ||
| Cost | 400 | 400 |
| Accumul. depr. | 75 | 35 |
| Carrying amount | 325 | 365 |
| Total assets | 525 | 595 |
| Liabilities | ||
| Current liabilities | 150 | 205 |
| Non-current liabilities | 235 | 250 |
| Owners' equity | ||
| Retained earnings | 100 | 100 |
| Contributed equity | 40 | 40 |
| Total L and OE | 525 | 595 |
Note: all figures above and below are given in millions of dollars ($m).
Your friend is trying to find the net present value of an investment which:
- Costs $1 million initially (t=0); and
- Pays a single positive cash flow of $1.1 million in one year (t=1).
The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.
Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.
He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).
He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.
Your friend has listed a few different ways to find the NPV which are written down below.
Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##
Method 2: ##-1m + 1.1m - 1m \times 0.1 ##
Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##
Which of the above calculations give the correct NPV? Select the most correct answer.
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Value the following business project to manufacture a new product.
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $3m | |
| Expected sale price of equipment at end of project | $0.6m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $5 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense per year | 0 | |
| Tax rate | 30% | |
| Weighted average cost of capital after tax per annum | 10% | |
Notes
- The firm's current assets and current liabilities are $3m and $2m respectively right now. This net working capital will not be used in this project, it will be used in other unrelated projects.
Due to the project, current assets (mostly inventory) will grow by $2m initially (at t = 0), and then by $0.2m at the end of the first year (t=1).
Current liabilities (mostly trade creditors) will increase by $0.1m at the end of the first year (t=1).
At the end of the project, the net working capital accumulated due to the project can be sold for the same price that it was bought. - The project cost $0.5m to research which was incurred one year ago.
Assumptions
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 3% pa.
- All rates are given as effective annual rates.
- The business considering the project is run as a 'sole tradership' (run by an individual without a company) and is therefore eligible for a 50% capital gains tax discount when the equipment is sold, as permitted by the Australian Tax Office.
What is the expected net present value (NPV) of the project?
There are many ways to calculate a firm's free cash flow (FFCF), also called cash flow from assets (CFFA). Some include the annual interest tax shield in the cash flow and some do not.
Which of the below FFCF formulas include the interest tax shield in the cash flow?
###(1) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp### ###(2) \quad FFCF=NI + Depr - CapEx -ΔNWC + IntExp.(1-t_c)### ###(3) \quad FFCF=EBIT.(1-t_c )+ Depr- CapEx -ΔNWC+IntExp.t_c### ###(4) \quad FFCF=EBIT.(1-t_c) + Depr- CapEx -ΔNWC### ###(5) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC+IntExp.t_c### ###(6) \quad FFCF=EBITDA.(1-t_c )+Depr.t_c- CapEx -ΔNWC### ###(7) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC### ###(8) \quad FFCF=EBIT-Tax + Depr - CapEx -ΔNWC-IntExp.t_c### ###(9) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC### ###(10) \quad FFCF=EBITDA-Tax - CapEx -ΔNWC-IntExp.t_c###The formulas for net income (NI also called earnings), EBIT and EBITDA are given below. Assume that depreciation and amortisation are both represented by 'Depr' and that 'FC' represents fixed costs such as rent.
###NI=(Rev - COGS - Depr - FC - IntExp).(1-t_c )### ###EBIT=Rev - COGS - FC-Depr### ###EBITDA=Rev - COGS - FC### ###Tax =(Rev - COGS - Depr - FC - IntExp).t_c= \dfrac{NI.t_c}{1-t_c}###A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
Question 370 capital budgeting, NPV, interest tax shield, WACC, CFFA
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $600k | |
| Depreciation of equipment per year | $250k | |
| Expected sale price of equipment at end of project | $200k | |
| Revenue per job | $12k | |
| Variable cost per job | $4k | |
| Quantity of jobs per year | 120 | |
| Fixed costs per year, paid at the end of each year | $100k | |
| Interest expense in first year (at t=1) | $16.091k | |
| Interest expense in second year (at t=2) | $9.711k | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Levered cost of equity | 12.5% | |
| Market portfolio return | 10% | |
| Beta of assets | 1.24 | |
| Beta of levered equity | 1.5 | |
| Firm's and project's debt-to-equity ratio | 25% | |
Notes
- The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
- Thousands are represented by 'k' (kilo).
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are nominal. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
Question 543 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to triple every 5 years, what must be the expected future capital return, given as an effective annual rate?
You deposit money into a bank. Which of the following statements is NOT correct? You:
Question 740 real and nominal returns and cash flows, DDM, inflation
Taking inflation into account when using the DDM can be hard. Which of the following formulas will NOT give a company's current stock price ##(P_0)##? Assume that the annual dividend was just paid ##(C_0)##, and the next dividend will be paid in one year ##(C_1)##.
A stock is expected to pay a dividend of $1 in one year. Its future annual dividends are expected to grow by 10% pa. So the first dividend of $1 is in one year, and the year after that the dividend will be $1.1 (=1*(1+0.1)^1), and a year later $1.21 (=1*(1+0.1)^2) and so on forever.
Its required total return is 30% pa. The total required return and growth rate of dividends are given as effective annual rates. The stock is fairly priced.
Calculate the pay back period of buying the stock and holding onto it forever, assuming that the dividends are received as at each time, not smoothly over each year.
A share will pay its next dividend of ##C_1## in one year, and will continue to pay a dividend every year after that forever, growing at a rate of ##g##. So the next dividend will be ##C_2=C_1 (1+g)^1##, then ##C_3=C_2 (1+g)^1##, and so on forever.
The current price of the share is ##P_0## and its required return is ##r##
Which of the following is NOT equal to the expected share price in 2 years ##(P_2)## just after the dividend at that time ##(C_2)## has been paid?
Question 748 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $2 tonight if you buy it today.
Thereafter the annual dividend is expected to grow by 3% pa, so the next dividend after the $2 one tonight will be $2.06 in one year, then in two years it will be $2.1218 and so on. The stock's required return is 8% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
Question 749 Multiples valuation, PE ratio, price to revenue ratio, price to book ratio, NPV
A real estate agent says that the price of a house in Sydney Australia is approximately equal to the gross weekly rent times 1000.
What type of valuation method is the real estate agent using?
Itau Unibanco is a major listed bank in Brazil with a market capitalisation of equity equal to BRL 85.744 billion, EPS of BRL 3.96 and 2.97 billion shares on issue.
Banco Bradesco is another major bank with total earnings of BRL 8.77 billion and 2.52 billion shares on issue.
Estimate Banco Bradesco's current share price using a price-earnings multiples approach assuming that Itau Unibanco is a comparable firm.
Note that BRL is the Brazilian Real, their currency. Figures sourced from Google Finance on the market close of the BVMF on 24 July 2015.
Question 758 time calculation, fully amortising loan, no explanation
Two years ago you entered into a fully amortising home loan with a principal of $1,000,000, an interest rate of 6% pa compounding monthly with a term of 25 years.
Then interest rates suddenly fall to 4.5% pa (t=0), but you continue to pay the same monthly home loan payments as you did before. How long will it now take to pay off your home loan? Measure the time taken to pay off the home loan from the current time which is 2 years after the home loan was first entered into.
Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 2, which was the 24th payment since the loan was granted. Also assume that rates were and are expected to remain constant.
Question 759 time calculation, fully amortising loan, no explanation
Five years ago you entered into a fully amortising home loan with a principal of $500,000, an interest rate of 4.5% pa compounding monthly with a term of 25 years.
Then interest rates suddenly fall to 3% pa (t=0), but you continue to pay the same monthly home loan payments as you did before. How long will it now take to pay off your home loan? Measure the time taken to pay off the home loan from the current time which is 5 years after the home loan was first entered into.
Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 5, which was the 60th payment since the loan was granted. Also assume that rates were and are expected to remain constant.
Question 760 time calculation, interest only loan, no explanation
Five years ago (##t=-5## years) you entered into an interest-only home loan with a principal of $500,000, an interest rate of 4.5% pa compounding monthly with a term of 25 years.
Then interest rates suddenly fall to 3% pa (##t=0##), but you continue to pay the same monthly home loan payments as you did before. Will your home loan be paid off by the end of its remaining term? If so, in how many years from now? Measure the time taken to pay off the home loan from the current time which is 5 years after the home loan was first entered into.
Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 5, which was the 60th payment since the loan was granted. Also assume that rates were and are expected to remain constant.
The phone company Optus have 2 mobile service plans on offer which both have the same amount of phone call, text message and internet data credit. Both plans have a contract length of 24 months and the monthly cost is payable in advance. The only difference between the two plans is that one is a:
- 'Bring Your Own' (BYO) mobile service plan, costing $80 per month. There is no phone included in this plan. The other plan is a:
- 'Bundled' mobile service plan that comes with the latest smart phone, costing $100 per month. This plan includes the latest smart phone.
Neither plan has any additional payments at the start or end. Assume that the discount rate is 1% per month given as an effective monthly rate.
The only difference between the plans is the phone, so what is the implied cost of the phone as a present value? Given that the latest smart phone actually costs $600 to purchase outright from another retailer, should you commit to the BYO plan or the bundled plan?
Radio-Rentals.com offers the Apple iphone 5S smart phone for rent at $12.95 per week paid in advance on a 2 year contract. After renting the phone, you must return it to Radio-Rentals.
Kogan.com offers the Apple iphone 5S smart phone for sale at $699. You estimate that the phone will last for 3 years before it will break and be worthless.
Currently, the effective annual interest rate is 11.351%, the effective monthly interest rate 0.9% and the effective weekly interest rate is 0.207%. Assume that there are exactly 52 weeks per year and 12 months per year.
Find the equivalent annual cost of renting the phone and also buying the phone. The answers below are listed in the same order.
Diversification in a portfolio of two assets works best when the correlation between their returns is:
All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:
Question 559 variance, standard deviation, covariance, correlation
Which of the following statements about standard statistical mathematics notation is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.
What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.
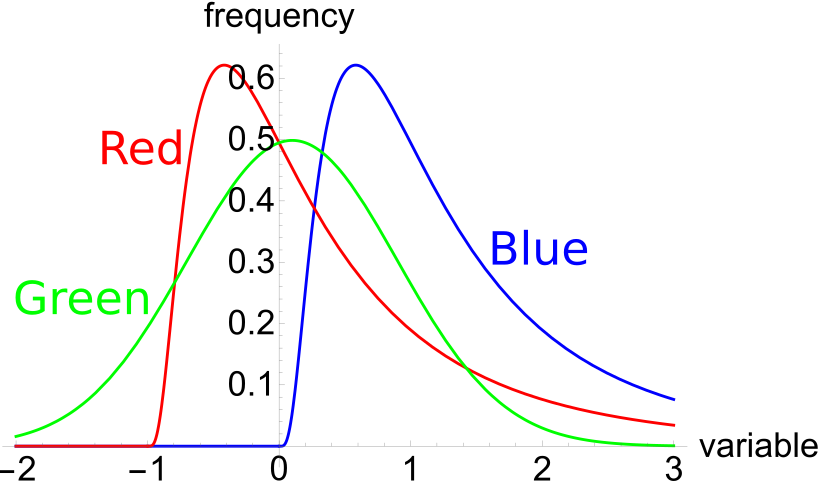
Which of the below statements is NOT correct?
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.

Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
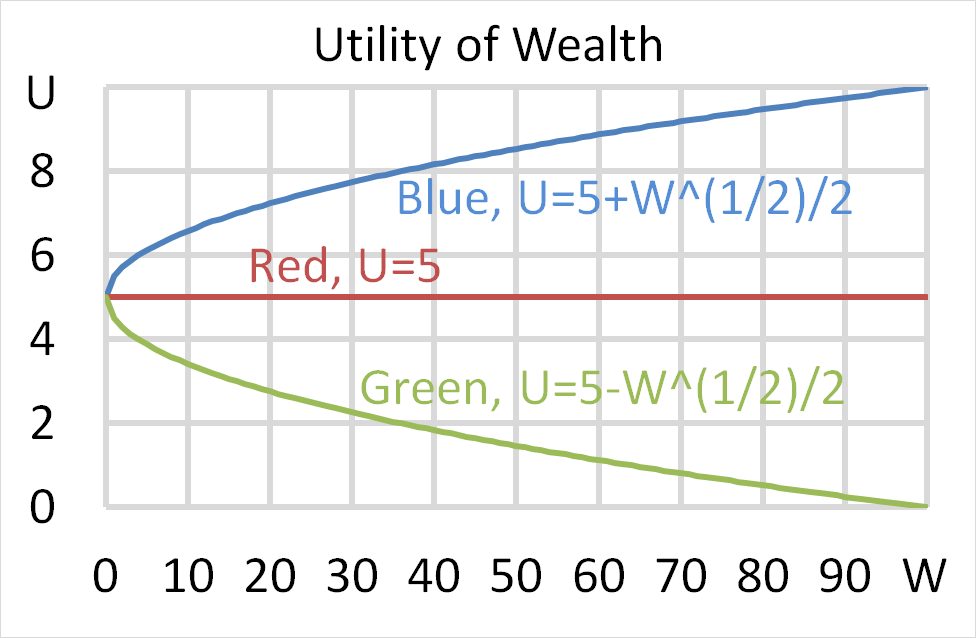
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
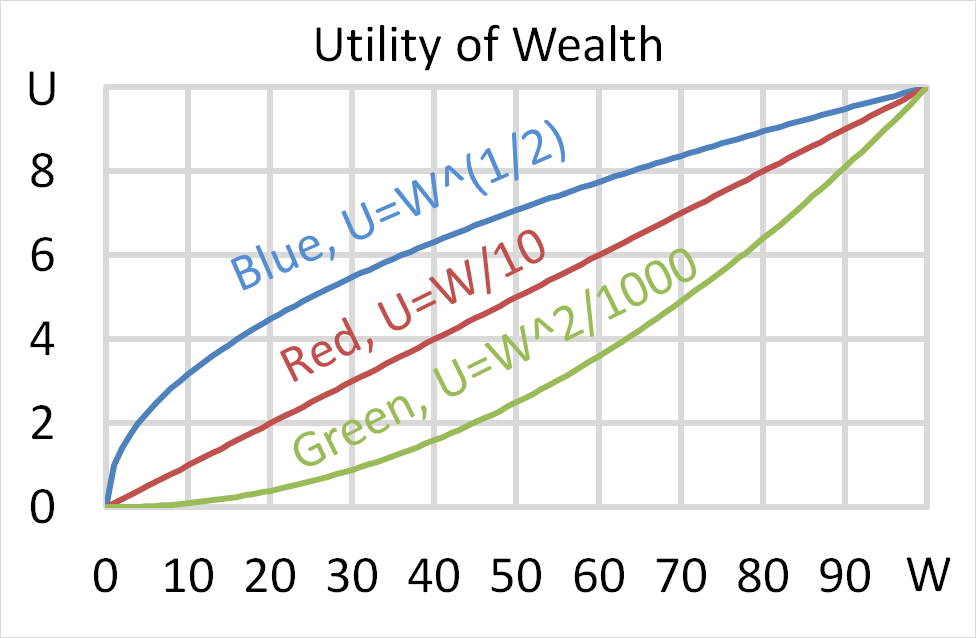
Mr Blue, Miss Red and Mrs Green are people with different utility functions. Which of the statements about the 3 utility functions is NOT correct?
A stock's required total return will increase when its:
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
Currently, a mining company has a share price of $6 and pays constant annual dividends of $0.50. The next dividend will be paid in 1 year. Suddenly and unexpectedly the mining company announces that due to higher than expected profits, all of these windfall profits will be paid as a special dividend of $0.30 in 1 year.
If investors believe that the windfall profits and dividend is a one-off event, what will be the new share price? If investors believe that the additional dividend is actually permanent and will continue to be paid, what will be the new share price? Assume that the required return on equity is unchanged. Choose from the following, where the first share price includes the one-off increase in earnings and dividends for the first year only ##(P_\text{0 one-off})## , and the second assumes that the increase is permanent ##(P_\text{0 permanent})##:
Note: When a firm makes excess profits they sometimes pay them out as special dividends. Special dividends are just like ordinary dividends but they are one-off and investors do not expect them to continue, unlike ordinary dividends which are expected to persist.
Question 568 rights issue, capital raising, capital structure
A company conducts a 1 for 5 rights issue at a subscription price of $7 when the pre-announcement stock price was $10. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order. Ignore all taxes, transaction costs and signalling effects.
In late 2003 the listed bank ANZ announced a 2-for-11 rights issue to fund the takeover of New Zealand bank NBNZ. Below is the chronology of events:
- 23/10/2003. Share price closes at $18.30.
- 24/10/2003. 2-for-11 rights issue announced at a subscription price of $13. The proceeds of the rights issue will be used to acquire New Zealand bank NBNZ. Trading halt announced in morning before market opens.
- 28/10/2003. Trading halt lifted. Last (and only) day that shares trade cum-rights. Share price opens at $18.00 and closes at $18.14.
- 29/10/2003. Shares trade ex-rights.
All things remaining equal, what would you expect ANZ's stock price to open at on the first day that it trades ex-rights (29/10/2003)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
There are a number of ways that assets can be depreciated. Generally the government's tax office stipulates a certain method.
But if it didn't, what would be the ideal way to depreciate an asset from the perspective of a businesses owner?
The hardest and most important aspect of business project valuation is the estimation of the:
Question 798 idiom, diversification, market efficiency, sunk cost, no explanation
The following quotes are most closely related to which financial concept?
- “Opportunity is missed by most people because it is dressed in overalls and looks like work” -Thomas Edison
- “The only place where success comes before work is in the dictionary” -Vidal Sassoon
- “The safest way to double your money is to fold it over and put it in your pocket” - Kin Hubbard
Question 800 leverage, portfolio return, risk, portfolio risk, capital structure, no explanation
Which of the following assets would you expect to have the highest required rate of return? All values are current market values.
Question 803 capital raising, rights issue, initial public offering, on market repurchase, no explanation
Which one of the following capital raisings or payouts involve the sale of shares to existing shareholders only?
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
A firm conducts a two-for-one stock split. Which of the following consequences would NOT be expected?
A graph of assets’ expected returns ##(\mu)## versus standard deviations ##(\sigma)## is given in the below diagram.
Each letter corresponds to a separate coloured area. The portfolios at the boundary of the areas, on the black lines, are excluded from each area. Assume that all assets represented in this graph are fairly priced, and that all risky assets can be short-sold.
Which of the following statements about this graph and Markowitz portfolio theory is NOT correct?
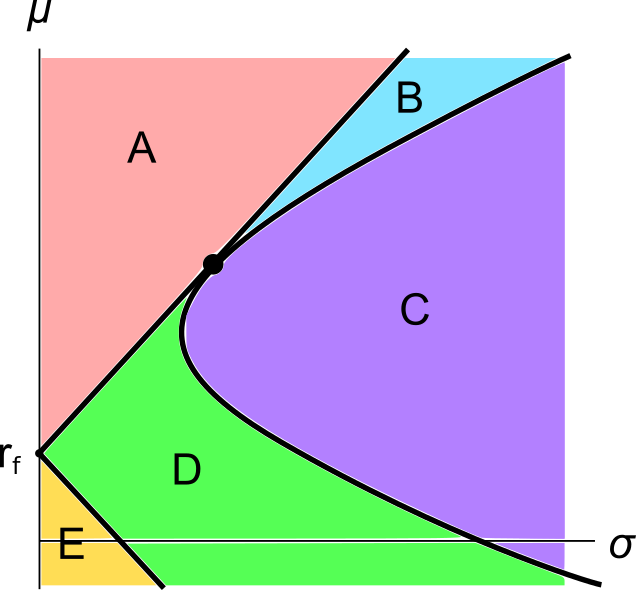
Question 809 Markowitz portfolio theory, CAPM, Jensens alpha, CML, systematic and idiosyncratic risk
A graph of assets’ expected returns ##(\mu)## versus standard deviations ##(\sigma)## is given in the graph below. The CML is the capital market line.
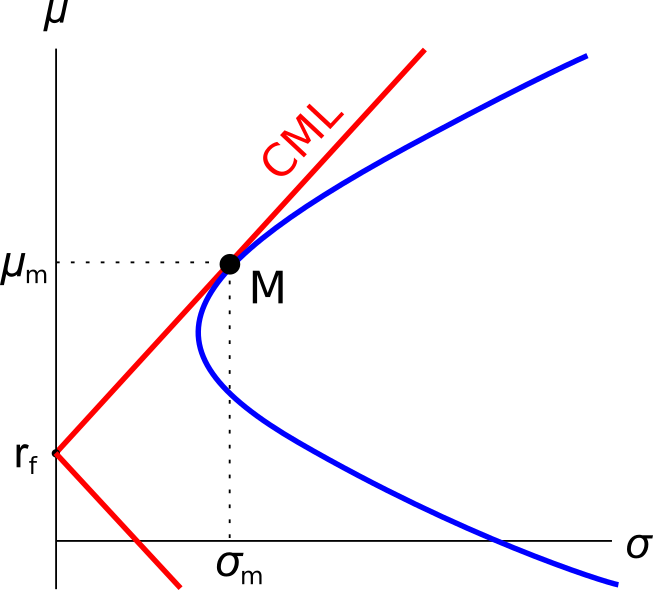
Which of the following statements about this graph, Markowitz portfolio theory and the Capital Asset Pricing Model (CAPM) theory is NOT correct?
Your friend wants to borrow $1,000 and offers to pay you back $100 in 6 months, with more $100 payments at the end of every month for another 11 months. So there will be twelve $100 payments in total. She says that 12 payments of $100 equals $1,200 so she's being generous.
If interest rates are 12% pa, given as an APR compounding monthly, what is the Net Present Value (NPV) of your friend's deal?
You are promised 20 payments of $100, where the first payment is immediate (t=0) and the last is at the end of the 19th year (t=19). The effective annual discount rate is ##r##.
Which of the following equations does NOT give the correct present value of these 20 payments?
Question 810 CAPM, systematic and idiosyncratic risk, market efficiency
Examine the graphs below. Assume that asset A is a single stock. Which of the following statements is NOT correct? Asset A:
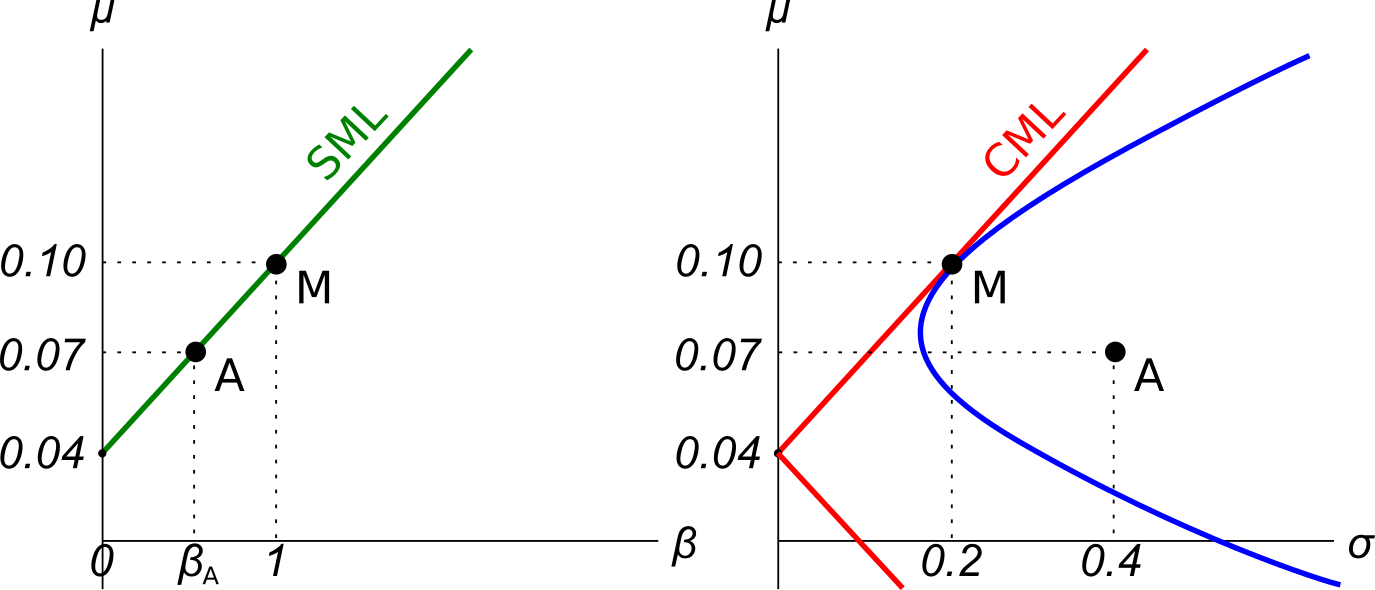
Let the 'income return' of a bond be the coupon at the end of the period divided by the market price now at the start of the period ##(C_1/P_0)##. The expected income return of a premium fixed coupon bond is:
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Of the 15% pa total expected return, the dividend yield is expected to always be 7% pa and rest is the capital yield.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% total return lasts for the next 100 years (t=0 to 100), then reverts to 10% after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant, the dividends can only be re-invested at 10% pa and all returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
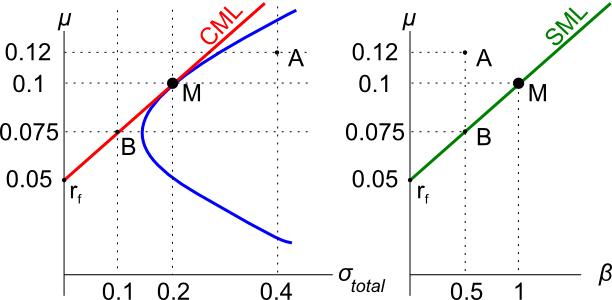
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
A stock's total standard deviation of returns is 20% pa. The market portfolio's total standard deviation of returns is 15% pa. The beta of the stock is 0.8.
What is the stock's diversifiable standard deviation?
A firm has a debt-to-assets ratio of 20%. What is its debt-to-equity ratio?
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 2 for 3 rights issue at a subscription price of $8 when the pre-announcement stock price was $9. Assume that all investors use their rights to buy those extra shares.
What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
Question 699 utility, risk aversion, utility function, gamble
Mr Blue, Miss Red and Mrs Green are people with different utility functions.
Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

Question 811 log-normal distribution, mean and median returns, return distribution, arithmetic and geometric averages
Which of the following statements about probability distributions is NOT correct?
Question 566 capital structure, capital raising, rights issue, on market repurchase, dividend, stock split, bonus issue
A company's share price fell by 20% and its number of shares rose by 25%. Assume that there are no taxes, no signalling effects and no transaction costs.
Which one of the following corporate events may have happened?