Question 24 implicit interest rate in wholesale credit, effective rate
A bathroom and plumbing supplies shop offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given in this question are effective annual rates.
A 180-day Bank Accepted Bill has a face value of $1,000,000. The interest rate is 8% pa and there are 365 days in the year. What is its price now?
A share was bought for $20 (at t=0) and paid its annual dividend of $3 one year later (at t=1). Just after the dividend was paid, the share price was $16 (at t=1). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Question 50 DDM, stock pricing, inflation, real and nominal returns and cash flows
Most listed Australian companies pay dividends twice per year, the 'interim' and 'final' dividends, which are roughly 6 months apart.
You are an equities analyst trying to value the company BHP. You decide to use the Dividend Discount Model (DDM) as a starting point, so you study BHP's dividend history and you find that BHP tends to pay the same interim and final dividend each year, and that both grow by the same rate.
You expect BHP will pay a $0.55 interim dividend in six months and a $0.55 final dividend in one year. You expect each to grow by 4% next year and forever, so the interim and final dividends next year will be $0.572 each, and so on in perpetuity.
Assume BHP's cost of equity is 8% pa. All rates are quoted as nominal effective rates. The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What is the current price of a BHP share?
You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.
You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.
At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?
Question 64 inflation, real and nominal returns and cash flows, APR, effective rate
In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.
The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
A company has:
- 50 million shares outstanding.
- The market price of one share is currently $6.
- The risk-free rate is 5% and the market return is 10%.
- Market analysts believe that the company's ordinary shares have a beta of 2.
- The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
- The company's debentures are publicly traded and their market price is equal to 90% of their face value.
- The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.
What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
Which statement(s) are correct?
(i) All stocks that plot on the Security Market Line (SML) are fairly priced.
(ii) All stocks that plot above the Security Market Line (SML) are overpriced.
(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.
Select the most correct response:
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
Your neighbour asks you for a loan of $100 and offers to pay you back $120 in one year.
You don't actually have any money right now, but you can borrow and lend from the bank at a rate of 10% pa. Rates are given as effective annual rates.
Assume that your neighbour will definitely pay you back. Ignore interest tax shields and transaction costs.
The Net Present Value (NPV) of lending to your neighbour is $9.09. Describe what you would do to actually receive a $9.09 cash flow right now with zero net cash flows in the future.
A 90-day $1 million Bank Accepted Bill (BAB) was bought for $990,000 and sold 30 days later for $996,000 (at t=30 days).
What was the total return, capital return and income return over the 30 days it was held?
Despite the fact that money market instruments such as bills are normally quoted with simple interest rates, please calculate your answers as compound interest rates, specifically, as effective 30-day rates, which is how the below answer choices are listed.
##r_\text{total}##, ##r_\text{capital}##, ## r_\text{income}##
An equity index is currently at 5,000 points. The 2 year futures price is 5,400 points and the total required return is 8% pa with continuous compounding. Each index point is worth $25.
What is the implied continuous dividend yield as a continuously compounded rate per annum?
One year ago you bought a $1,000,000 house partly funded using a mortgage loan. The loan size was $800,000 and the other $200,000 was your wealth or 'equity' in the house asset.
The interest rate on the home loan was 4% pa.
Over the year, the house produced a net rental yield of 2% pa and a capital gain of 2.5% pa.
Assuming that all cash flows (interest payments and net rental payments) were paid and received at the end of the year, and all rates are given as effective annual rates, what was the total return on your wealth over the past year?
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
The current gold price is $700, gold storage costs are 2% pa and the risk free rate is 10% pa, both with continuous compounding.
What should be the 3 year gold futures price?
A stock is expected to pay a dividend of $5 per share in 1 month and $5 again in 7 months.
The stock price is $100, and the risk-free rate of interest is 10% per annum with continuous compounding. The yield curve is flat. Assume that investors are risk-neutral.
An investor has just taken a short position in a one year forward contract on the stock.
Find the forward price ##(F_1)## and value of the contract ##(V_0)## initially. Also find the value of the short futures contract in 6 months ##(V_\text{0.5, SF})## if the stock price fell to $90.
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
In general, stock prices tend to rise. What does this mean for futures on equity?
The price of gold is currently $700 per ounce. The forward price for delivery in 1 year is $800. An arbitrageur can borrow money at 10% per annum given as an effective discrete annual rate. Assume that gold is fairly priced and the cost of storing gold is zero.
What is the best way to conduct an arbitrage in this situation? The best arbitrage strategy requires zero capital, has zero risk and makes money straight away. An arbitrageur should sell 1 forward on gold and:
Question 598 future, tailing the hedge, cross hedging
The standard deviation of monthly changes in the spot price of lamb is $0.015 per pound. The standard deviation of monthly changes in the futures price of live cattle is $0.012 per pound. The correlation between the spot price of lamb and the futures price of cattle is 0.4.
It is now January. A lamb producer is committed to selling 1,000,000 pounds of lamb in May. The spot price of live cattle is $0.30 per pound and the June futures price is $0.32 per pound. The spot price of lamb is $0.60 per pound.
The producer wants to use the June live cattle futures contracts to hedge his risk. Each futures contract is for the delivery of 50,000 pounds of cattle.
How many live cattle futures should the lamb farmer sell to hedge his risk? Round your answer to the nearest whole number of contracts.
In February a company sold one December 40,000 pound (about 18 metric tons) lean hog futures contract. It closed out its position in May.
The spot price was $0.68 per pound in February. The December futures price was $0.70 per pound when the trader entered into the contract in February, $0.60 when he closed out his position in May, and $0.55 when the contract matured in December.
What was the total profit?
An equity index fund manager controls a USD1 billion diversified equity portfolio with a beta of 1.3. The equity manager fears that a global recession will begin in the next year, causing equity prices to tumble. The market does not think that this will happen. If the fund manager wishes to reduce her portfolio beta to 0.5, how many S&P500 futures should she sell?
The US market equity index is the S&P500. One year CME futures on the S&P500 currently trade at 2,062 points and the spot price is 2,091 points. Each point is worth $250. How many one year S&P500 futures contracts should the fund manager sell?
What derivative position are you exposed to if you have the obligation to sell the underlying asset at maturity, so you will definitely be forced to sell the underlying asset?
Question 829 option, future, delta, gamma, theta, no explanation
Below are some statements about futures and European-style options on non-dividend paying stocks. Assume that the risk free rate is always positive. Which of these statements is NOT correct? All other things remaining equal:
A put option written on a risky non-dividend paying stock will mature in one month. As is normal, assume that the option's exercise price is non-zero and positive ##(K>0)## and the stock has limited liability ##(S>0)##.
Which of the following statements is NOT correct? The put option's:
Question 833 option, delta, theta, standard deviation, no explanation
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
Question 834 option, delta, theta, gamma, standard deviation, Black-Scholes-Merton option pricing
Which of the following statements about an option (either a call or put) and its underlying stock is NOT correct?
| European Call Option | ||
| on a non-dividend paying stock | ||
| Description | Symbol | Quantity |
| Spot price ($) | ##S_0## | 20 |
| Strike price ($) | ##K_T## | 18 |
| Risk free cont. comp. rate (pa) | ##r## | 0.05 |
| Standard deviation of the stock's cont. comp. returns (pa) | ##\sigma## | 0.3 |
| Option maturity (years) | ##T## | 1 |
| Call option price ($) | ##c_0## | 3.939488 |
| Delta | ##\Delta = N[d_1]## | 0.747891 |
| ##N[d_2]## | ##N[d_2]## | 0.643514 |
| Gamma | ##\Gamma## | 0.053199 |
| Theta ($/year) | ##\Theta = \partial c / \partial T## | 1.566433 |
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue. Let ##P_1## be the unknown price of a stock in one year. ##P_1## is a random variable. Let ##P_0 = 1##, so the share price now is $1. This one dollar is a constant, it is not a variable.

Which of the below statements is NOT correct? Financial practitioners commonly assume that the shape of the PDF represented in the colour:
Question 723 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 99 | -0.010050 | 0.990000 | -0.010000 |
| 2 | 180.40 | 0.600057 | 1.822222 | 0.822222 |
| 3 | 112.73 | 0.470181 | 0.624889 | 0.375111 |
| Arithmetic average | 0.0399 | 1.1457 | 0.1457 | |
| Arithmetic standard deviation | 0.4384 | 0.5011 | 0.5011 | |
Question 928 mean and median returns, mode return, return distribution, arithmetic and geometric averages, continuously compounding rate, no explanation
The arithmetic average continuously compounded or log gross discrete return (AALGDR) on the ASX200 accumulation index over the 24 years from 31 Dec 1992 to 31 Dec 2016 is 9.49% pa.
The arithmetic standard deviation (SDLGDR) is 16.92 percentage points pa.
Assume that the log gross discrete returns are normally distributed and that the above estimates are true population statistics, not sample statistics, so there is no standard error in the sample mean or standard deviation estimates. Also assume that the standardised normal Z-statistic corresponding to a one-tail probability of 2.5% is exactly -1.96.
If you had a $1 million fund that replicated the ASX200 accumulation index, in how many years would the mode dollar value of your fund first be expected to lie outside the 95% confidence interval forecast?
Note that the mode of a log-normally distributed future price is: ##P_{T \text{ mode}} = P_0.e^{(\text{AALGDR} - \text{SDLGDR}^2 ).T} ##
Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?
Which firms tend to have high forward-looking price-earnings (PE) ratios?
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
Question 749 Multiples valuation, PE ratio, price to revenue ratio, price to book ratio, NPV
A real estate agent says that the price of a house in Sydney Australia is approximately equal to the gross weekly rent times 1000.
What type of valuation method is the real estate agent using?
A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?
Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
There are a number of ways that assets can be depreciated. Generally the government's tax office stipulates a certain method.
But if it didn't, what would be the ideal way to depreciate an asset from the perspective of a businesses owner?
Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').
How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:
Annual interest expense is equal to:
Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Piano Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 310 | |
| COGS | 185 | |
| Operating expense | 20 | |
| Depreciation | 15 | |
| Interest expense | 10 | |
| Income before tax | 80 | |
| Tax at 30% | 24 | |
| Net income | 56 | |
| Piano Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 240 | 230 |
| PPE | ||
| Cost | 420 | 400 |
| Accumul. depr. | 50 | 35 |
| Carrying amount | 370 | 365 |
| Total assets | 610 | 595 |
| Liabilities | ||
| Current liabilities | 180 | 190 |
| Non-current liabilities | 290 | 265 |
| Owners' equity | ||
| Retained earnings | 90 | 90 |
| Contributed equity | 50 | 50 |
| Total L and OE | 610 | 595 |
Note: all figures are given in millions of dollars ($m).
A company increases the proportion of debt funding it uses to finance its assets by issuing bonds and using the cash to repurchase stock, leaving assets unchanged.
Ignoring the costs of financial distress, which of the following statements is NOT correct:
Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Scubar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 200 | |
| COGS | 60 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 90 | |
| Taxes at 30% | 27 | |
| Net income | 63 | |
| Scubar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 60 | 50 |
| Trade debtors | 19 | 6 |
| Rent paid in advance | 3 | 2 |
| PPE | 420 | 400 |
| Total assets | 502 | 458 |
| Trade creditors | 10 | 8 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 130 | 130 |
| Retained profits | 162 | 130 |
| Total L and OE | 502 | 458 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Read the following financial statements and calculate the firm's free cash flow over the 2014 financial year.
| UBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2014 | ||
| $m | ||
| Sales | 293 | |
| COGS | 200 | |
| Rent expense | 15 | |
| Gas expense | 8 | |
| Depreciation | 10 | |
| EBIT | 60 | |
| Interest expense | 0 | |
| Taxable income | 60 | |
| Taxes | 18 | |
| Net income | 42 | |
| UBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2014 | 2013 |
| $m | $m | |
| Assets | ||
| Cash | 30 | 29 |
| Accounts receivable | 5 | 7 |
| Pre-paid rent expense | 1 | 0 |
| Inventory | 50 | 46 |
| PPE | 290 | 300 |
| Total assets | 376 | 382 |
| Liabilities | ||
| Trade payables | 20 | 18 |
| Accrued gas expense | 3 | 2 |
| Non-current liabilities | 0 | 0 |
| Contributed equity | 212 | 212 |
| Retained profits | 136 | 150 |
| Asset revaluation reserve | 5 | 0 |
| Total L and OE | 376 | 382 |
Note: all figures are given in millions of dollars ($m).
The firm's free cash flow over the 2014 financial year was:
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
Question 903 option, Black-Scholes-Merton option pricing, option on stock index
A six month European-style call option on the S&P500 stock index has a strike price of 2800 points.
The underlying S&P500 stock index currently trades at 2700 points, has a continuously compounded dividend yield of 2% pa and a standard deviation of continuously compounded returns of 25% pa.
The risk-free interest rate is 5% pa continuously compounded.
Use the Black-Scholes-Merton formula to calculate the option price. The call option price now is:
Question 99 capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.
Assume that:
- The firm and individual investors can borrow at the same rate and have the same tax rates.
- The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
- There are no market frictions relating to debt such as asymmetric information or transaction costs.
- Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.
According to Miller and Modigliani's theory, which statement is correct?
Question 988 variance, covariance, beta, CAPM, risk, no explanation
| Price Data Time Series | |||||||||||
| Sourced from Yahoo Finance Historical Price Data | |||||||||||
| Date | S&P500 Index (^GSPC) | Apple (AAPL) | |||||||||
| Open | High | Low | Close | Adj close | Open | High | Low | Close | Adj close | ||
| 2007, Wed 3 Jan | 1418 | 1429 | 1408 | 1417 | 1417 | 12.33 | 12.37 | 11.7 | 11.97 | 10.42 | |
| 2008, Wed 2 Jan | 1468 | 1472 | 1442 | 1447 | 1447 | 28.47 | 28.61 | 27.51 | 27.83 | 24.22 | |
| 2009, Fri 2 Jan | 903 | 935 | 899 | 932 | 932 | 12.27 | 13.01 | 12.17 | 12.96 | 11.28 | |
| 2010, Mon 4 Jan | 1117 | 1134 | 1117 | 1133 | 1133 | 30.49 | 30.64 | 30.34 | 30.57 | 26.6 | |
| Source: Yahoo Finance. | |||||||||||
Which of the following statements about the above table which is used to calculate Apple's equity beta is NOT correct?
Question 578 inflation, real and nominal returns and cash flows
Which of the following statements about inflation is NOT correct?
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
Question 740 real and nominal returns and cash flows, DDM, inflation
Taking inflation into account when using the DDM can be hard. Which of the following formulas will NOT give a company's current stock price ##(P_0)##? Assume that the annual dividend was just paid ##(C_0)##, and the next dividend will be paid in one year ##(C_1)##.
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):
###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###
Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:
###r_\text{total}=r_\text{income}+r_\text{capital}###
So the total return of an asset is the income component plus the capital or price growth component.
Another way to break up total return is to use the Capital Asset Pricing Model:
###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###
###r_\text{total}=r_\text{time value}+r_\text{risk premium}###
So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.
Using the above theory and your general knowledge, which of the below equations, if any, are correct?
(I) ##r_\text{income}=r_\text{time value}##
(II) ##r_\text{income}=r_\text{risk premium}##
(III) ##r_\text{capital}=r_\text{time value}##
(IV) ##r_\text{capital}=r_\text{risk premium}##
(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##
Which of the equations are correct?
Question 271 CAPM, option, risk, systematic risk, systematic and idiosyncratic risk
All things remaining equal, according to the capital asset pricing model, if the systematic variance of an asset increases, its required return will increase and its price will decrease.
If the idiosyncratic variance of an asset increases, its price will be unchanged.
What is the relationship between the price of a call or put option and the total, systematic and idiosyncratic variance of the underlying asset that the option is based on? Select the most correct answer.
Call and put option prices increase when the:
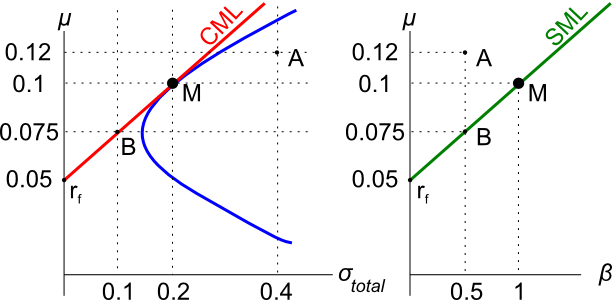
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?
Question 807 market efficiency, expected and historical returns, CAPM, beta, systematic risk, no explanation
You work in Asia and just woke up. It looked like a nice day but then you read the news and found out that last night the American share market fell by 10% while you were asleep due to surprisingly poor macro-economic world news. You own a portfolio of liquid stocks listed in Asia with a beta of 1.6. When the Asian equity markets open, what do you expect to happen to your share portfolio? Assume that the capital asset pricing model (CAPM) is correct and that the market portfolio contains all shares in the world, of which American shares are a big part. Your portfolio beta is measured against this world market portfolio.
When the Asian equity market opens for trade, you would expect your portfolio value to:
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
Question 180 equivalent annual cash flow, inflation, real and nominal returns and cash flows
Details of two different types of light bulbs are given below:
- Low-energy light bulbs cost $3.50, have a life of nine years, and use about $1.60 of electricity a year, paid at the end of each year.
- Conventional light bulbs cost only $0.50, but last only about a year and use about $6.60 of energy a year, paid at the end of each year.
The real discount rate is 5%, given as an effective annual rate. Assume that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the Equivalent Annual Cost (EAC) of the low-energy and conventional light bulbs. The below choices are listed in that order.
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 363 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 8% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 529 DDM, real and nominal returns and cash flows, inflation, real estate, no explanation
If housing rents are constrained from growing more than the maximum target inflation rate, and houses can be priced as a perpetuity of growing net rental cash flows, then what is the implication for house prices, all things remaining equal? Select the most correct answer.
Background: Since 1990, many central banks across the world have become 'inflation targeters'. They have adopted a policy of trying to keep inflation in a predictable narrow range, with the hope of encouraging long-term lending to fund more investment and maintain higher GDP growth.
Australia's central bank, the Reserve Bank of Australia (RBA), has specifically stated their inflation target range is between 2 and 3% pa.
Some Australian residential property market commentators suggest that because rental costs comprise a large part of the Australian consumer price index (CPI), rent costs across the nation cannot significantly exceed the maximum inflation target range of 3% pa without the prices of other goods growing by less than the target range for long periods, which is unlikely.