Fight Finance

Question 404  income and capital returns, real estate

One and a half years ago Frank bought a house for $600,000. Now it's worth only $500,000, based on recent similar sales in the area.

The expected total return on Frank's residential property is 7% pa.

He rents his house out for $1,600 per month, paid in advance. Every 12 months he plans to increase the rental payments.

The present value of 12 months of rental payments is $18,617.27.

The future value of 12 months of rental payments one year in the future is $19,920.48.

What is the expected annual rental yield of the property? Ignore the costs of renting such as maintenance, real estate agent fees and so on.

(a) 3.1029%

(b) 3.3201%

(c) 3.7235%

(d) 3.9841%

(e) 7%

Question 461  book and market values, ROE, ROA, market efficiency

One year ago a pharmaceutical firm floated by selling its 1 million shares for $100 each. Its book and market values of equity were both $100m. Its debt totalled $50m. The required return on the firm's assets was 15%, equity 20% and debt 5% pa.

In the year since then, the firm:

• Earned net income of $29m.
• Paid dividends totaling $10m.
• Discovered a valuable new drug that will lead to a massive 1,000 times increase in the firm's net income in 10 years after the research is commercialised. News of the discovery was publicly announced. The firm's systematic risk remains unchanged.

Which of the following statements is NOT correct? All statements are about current figures, not figures one year ago.

(a) The book value of equity would be larger than the market value of equity.

(b) The book ROA from accounting would be larger than the required return on assets from finance.

(c) The book ROE from accounting would be larger than the required return on equity from finance.

(d) The book ROE would be larger than the book ROA.

(e) The required return on equity would be larger than the required return on assets.

Hint: Book return on assets (ROA) and book return on equity (ROE) are ratios that accountants like to use to measure a business's past performance.

###\text{ROA}= \dfrac{\text{Net income}}{\text{Book value of assets}}###

###\text{ROE}= \dfrac{\text{Net income}}{\text{Book value of equity}}###

The required return on assets ##r_V## is a return that financiers like to use to estimate a business's future required performance which compensates them for the firm's assets' risks. If the business were to achieve realised historical returns equal to its required returns, then investment into the business's assets would have been a zero-NPV decision, which is neither good nor bad but fair.

###r_\text{V, 0 to 1}= \dfrac{\text{Cash flow from assets}_\text{1}}{\text{Market value of assets}_\text{0}} = \dfrac{CFFA_\text{1}}{V_\text{0}}###

Similarly for equity and debt.

Question 575  inflation, real and nominal returns and cash flows

You expect a nominal payment of $100 in 5 years. The real discount rate is 10% pa and the inflation rate is 3% pa. Which of the following statements is NOT correct?

(a) The nominal cash flow of $100 in 5 years is equivalent to a real cash flow of $86.2609 in 5 years. This means that $86.2609 will buy the same amount of goods and services now as $100 will buy in 5 years.

(b) The real discount rate of 10% pa is equivalent to a nominal discount rate of 13.3333% pa.

(c) The nominal price of goods and services will increase by 3% every year.

(d) The real price of goods and services will increase by 3% every year.

(e) The present value of your payment will increase by the nominal discount rate every year.

Question 49  inflation, real and nominal returns and cash flows, APR, effective rate

In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.

The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.

What is the real yield on these bonds, given as an APR compounding every 6 months?

(a) 0.3086%

(b) 0.6171%

(c) 0.6181%

(d) 0.6239%

(e) 0.6300%

Question 64  inflation, real and nominal returns and cash flows, APR, effective rate

In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.

The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.

What is the real yield on these bonds, given as an APR compounding every 6 months?

(a) -1.3529627%

(b) -0.4977348%

(c) 0.4977348%

(d) 1.3529627%

(e) 1.3621776%

Question 8  DDM

For a price of $10.20 each, Renee will sell you 100 shares. Each share is expected to pay dividends in perpetuity, growing at a rate of 5% pa. The next dividend is one year away (t=1) and is expected to be $1 per share.

The required return of the stock is 15% pa.

Would you like to the shares or politely ?

Question 105  NPV, risk, market efficiency

A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.

What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).

(a) $10

(b) $3

(c) $2.8037

(d) $2.7273

(e) $0

Question 125  option, speculation, market efficiency

Suppose that the US government recently announced that subsidies for fresh milk producers will be gradually phased out over the next year. Newspapers say that there are expectations of a 40% increase in the spot price of fresh milk over the next year.

Option prices on fresh milk trading on the Chicago Mercantile Exchange (CME) reflect expectations of this 40% increase in spot prices over the next year. Similarly to the rest of the market, you believe that prices will rise by 40% over the next year.

What option trades are likely to be profitable, or to be more specific, result in a positive Net Present Value (NPV)?

Assume that:

• Only the spot price is expected to increase and there is no change in expected volatility or other variables that affect option prices.
• No taxes, transaction costs, information asymmetry, bid-ask spreads or other market frictions.

(a) Buy one year call options on fresh milk.

(b) Buy one year put options on fresh milk.

(c) Sell one year call options on fresh milk.

(d) All of the above option trades are likely to have a positive NPV.

(e) None of the above option trades are likely to have a positive NPV.

Question 3  DDM, income and capital returns

The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###

What is ##g##? The value ##g## is the long term expected:

(a) Income return of the stock.

(b) Capital return of the stock.

(c) Total return of the stock.

(d) Dividend yield of the stock.

(e) Price-earnings ratio of the stock.

Question 55  NPV, DDM

A stock is expected to pay the following dividends:

Cash Flows of a Stock
Time (yrs)	0	1	2	3	4	...
Dividend ($)	0.00	1.15	1.10	1.05	1.00	...

After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,

• the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
• the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.

The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.

What will be the price of the stock in four and a half years (t = 4.5)?

(a) $5.2615

(b) $6.0386

(c) $6.3333

(d) $6.6425

(e) $11.9040

Question 497  income and capital returns, DDM, ex dividend date

A stock will pay you a dividend of $10 tonight if you buy it today. Thereafter the annual dividend is expected to grow by 5% pa, so the next dividend after the $10 one tonight will be $10.50 in one year, then in two years it will be $11.025 and so on. The stock's required return is 10% pa.

What is the stock price today and what do you expect the stock price to be tomorrow, approximately?

(a) $200 today and $210 tomorrow.

(b) $210 today and $220 tomorrow.

(c) $220 today and $230 tomorrow.

(d) $210 today and $200 tomorrow.

(e) $220 today and $210 tomorrow.

Question 148  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

### p_0 = \frac{d_1}{r - g} ###

Which expression is NOT equal to the expected dividend yield?

(a) ## r-g ##

(b) ## \dfrac{d_1}{p_0} ##

(c) ## \dfrac{d_5}{p_4} ##

(d) ## \dfrac{d_5(1+g)^2}{p_6} ##

(e) ## \dfrac{d_3}{p_0(1+r)^2} ##

Question 498  NPV, Annuity, perpetuity with growth, multi stage growth model

A business project is expected to cost $100 now (t=0), then pay $10 at the end of the third (t=3), fourth, fifth and sixth years, and then grow by 5% pa every year forever. So the cash flow will be $10.5 at the end of the seventh year (t=7), then $11.025 at the end of the eighth year (t=8) and so on perpetually. The total required return is 10℅ pa.

Which of the following formulas will NOT give the correct net present value of the project?

(a) ##-100+ \dfrac{ \dfrac{10}{0.1} \left(1-\dfrac{1}{(1+0.1)^3} \right)}{(1+0.1)^2} +\dfrac{\left(\dfrac{10}{0.1-0.05}\right)}{(1+0.1)^5} ##

(b) ##-100+ \dfrac{10}{(1+0.1)^3} +\dfrac{10}{(1+0.1)^4} +\dfrac{10}{(1+0.1)^5} +\dfrac{\left(\dfrac{10}{0.1-0.05}\right)}{(1+0.1)^5} ##

(c) ##-100+ \dfrac{ \dfrac{10}{0.1} \left(1-\dfrac{1}{(1+0.1)^4} \right)}{(1+0.1)^2} +\dfrac{\left(\dfrac{10.5}{0.1-0.05}\right)}{(1+0.1)^6} ##

(d) ##-100+ \dfrac{10}{(1+0.1)^3} +\dfrac{10}{(1+0.1)^4} +\dfrac{10}{(1+0.1)^5} +\dfrac{10}{(1+0.1)^6} +\dfrac{\left(\dfrac{10.5}{0.1-0.05}\right)}{(1+0.1)^6} ##

(e) ##-100+ \dfrac{ \dfrac{10}{0.1} \left(1-\dfrac{1}{(1+0.1)^3} \right)}{(1+0.1)^3} +\dfrac{\left(\dfrac{10}{0.1-0.05}\right)}{(1+0.1)^5} ##

Question 211  equivalent annual cash flow

You're advising your superstar client 40-cent who is weighing up buying a private jet or a luxury yacht. 40-cent is just as happy with either, but he wants to go with the more cost-effective option. These are the cash flows of the two options:

• The private jet can be bought for $6m now, which will cost $12,000 per month in fuel, piloting and airport costs, payable at the end of each month. The jet will last for 12 years.
• Or the luxury yacht can be bought for $4m now, which will cost $20,000 per month in fuel, crew and berthing costs, payable at the end of each month. The yacht will last for 20 years.

What's unusual about 40-cent is that he is so famous that he will actually be able to sell his jet or yacht for the same price as it was bought since the next generation of superstar musicians will buy it from him as a status symbol.

Bank interest rates are 10% pa, given as an effective annual rate. You can assume that 40-cent will live for another 60 years and that when the jet or yacht's life is at an end, he will buy a new one with the same details as above.

Would you advise 40-cent to buy the or the ?

Note that the effective monthly rate is ##r_\text{eff monthly}=(1+0.1)^{1/12}-1=0.00797414##

Question 457  PE ratio, Multiples valuation

Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.

(a) Highly liquid publically listed firms.

(b) Firms in a declining industry with very low or negative earnings growth.

(c) Firms expected to have temporarily low earnings over the next year, but with higher earnings later.

(d) Firms whose returns have a very low level of systematic risk.

(e) Firms whose assets include a very large proportion of cash.

Question 330  APR, effective rate, debt terminology

Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?

(a) Effective rates compound once over their time period. So an effective monthly rate compounds once per month.

(b) APR's compound more than once per year. So an APR compounding monthly compounds 12 times per year. The exception is an APR that compounds annually (once per year) which is the same thing as an effective annual rate.

(c) To convert an effective rate to an APR, multiply the effective rate by the number of time periods in one year. So an effective monthly rate multiplied by 12 is equal to an APR compounding monthly.

(d) To convert an APR compounding monthly to an effective monthly rate, divide the APR by the number of months in one year (12).

(e) To convert an APR compounding monthly to an effective weekly rate, divide the APR by the number of weeks in one year (approximately 52).

Question 290  APR, effective rate, debt terminology

Which of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?

(a) An effective annual rate could be called: "a yearly rate compounding per year".

(b) An APR compounding monthly could be called: "a yearly rate compounding per month".

(c) An effective monthly rate could be called: "a yearly rate compounding per month".

(d) An APR compounding daily could be called: "a yearly rate compounding per day".

(e) An effective 2-year rate could be called: "a 2-year rate compounding every 2 years".

Question 127  interest expense

A zero coupon bond that matures in 6 months has a face value of $1,000.

The firm that issued this bond is trying to forecast its income statement for the year. It needs to calculate the interest expense of the bond this year.

The bond is highly illiquid and hasn't traded on the market. But the finance department have assessed the bond's fair value to be $950 and this is its book value right now at the start of the year.

Assume that:

• the firm uses the 'effective interest method' to calculate interest expense.
• the market value of the bond is the same as the book value.
• the firm is only interested in this bond's interest expense. Do not include the interest expense for a new bond issued to refinance the current one, as would normally happen.

What will be the interest expense of the bond this year for the purpose of forecasting the income statement?

(a) $0

(b) $50.0000

(c) $51.3158

(d) $102.6316

(e) $1,000.0000

Question 223  CFFA, interest tax shield

Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?

(a) An increase in net capital spending.

(b) A decrease in the cash flow to creditors.

(c) An increase in interest expense.

(d) An increase in net working capital.

(e) A decrease in dividends paid.

Question 656  debt terminology

Which of the following statements is NOT correct? Lenders:

(a) Buy debt.

(b) Own debt.

(c) Are owed money.

(d) Write debt.

(e) Have debt assets.

Question 56  income and capital returns, bond pricing, premium par and discount bonds

Which of the following statements about risk free government bonds is NOT correct?

(a) Premium bonds have a positive expected capital return.

(b) Discount bonds have a positive expected capital return.

(c) Par bonds have a zero expected capital return.

(d) Par bonds have a total expected yield equal to their coupon yield.

(e) Zero coupon bonds selling at par would have zero expected total, income and capital yields.

Hint: Total return can be broken into income and capital returns as follows:

###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###

The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.

Question 239  income and capital returns, inflation, real and nominal returns and cash flows, interest only loan

A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.

From the bank's point of view, what is the long term expected nominal capital return of the loan asset?

(a) Approximately 6%.

(b) Approximately 4%.

(c) Approximately 2%.

(d) Approximately 0%.

(e) Approximately -2%.

Question 234  debt terminology

An 'interest only' loan can also be called a:

(a) Discount loan

(b) Par loan

(c) Premium loan

(d) Deferred repayment loan

(e) Fully amortising loan.

Question 138  bond pricing, premium par and discount bonds

Bonds A and B are issued by the same Australian company. Both bonds yield 7% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond A pays coupons of 10% pa and bond B pays coupons of 5% pa. Which of the following statements is true about the bonds' prices?

(a) The prices of bonds A and B will be more than $100.

(b) The prices of bonds A and B will be less than $100.

(c) Bond A will have a price more than $100, and bond B will have a price less than $100.

(d) Bond A will have a price less than $100, and bond B will have a price more than $100.

(e) Bonds A and B will both have a price of $100.

Question 153  bond pricing, premium par and discount bonds

Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100) and maturity (3 years).

The only difference is that bond X and Y's yields are 8 and 12% pa respectively. Which of the following statements is true?

(a) Bonds X and Y are premium bonds.

(b) Bonds X and Y are discount bonds.

(c) Bond X is a discount bond but bond Y is a premium bond.

(d) Bond X is a premium bond but bond Y is a discount bond.

(e) Bonds X and Y have the same price.

Question 207  income and capital returns, bond pricing, coupon rate, no explanation

For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?

Let: ##P_0## be the bond price now,

##F_T## be the bond's face value,

##T## be the bond's maturity in years,

##r_\text{total}## be the bond's total yield,

##r_\text{income}## be the bond's income yield,

##r_\text{capital}## be the bond's capital yield, and

##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.

(a) coupon rate = ##\dfrac{C_{0.5}+C_{1}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{total})^{0.5}+C_{1}}{P_0}##

(b) coupon rate = ##\dfrac{2 \times C_{0.5}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{capital})^{0.5}+C_{1}}{P_0}##

(c) coupon rate = ##\dfrac{2 \times C_{1}}{P_0}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}+C_{1}}{P_0}##

(d) coupon rate = ##\dfrac{2 \times C_{1}}{P_0}##, ##r_\text{income, 0 to 1}=\dfrac{2 \times C_{1}}{P_0}##

(e) coupon rate = ##\dfrac{2 \times C_{1}}{F_T}##, ##r_\text{income, 0 to 1}=\dfrac{C_{0.5}(1+r_\text{total})^{0.5}+C_{1}}{F_T}##

Question 732  real and nominal returns and cash flows, inflation, income and capital returns

An investor bought a bond for $100 (at t=0) and one year later it paid its annual coupon of $1 (at t=1). Just after the coupon was paid, the bond price was $100.50 (at t=1). Inflation over the past year (from t=0 to t=1) was 3% pa, given as an effective annual rate.

Which of the following statements is NOT correct? The bond investment produced a:

(a) Nominal income return of 1% pa ##\left( =\dfrac{1}{100} \right)##.

(b) Nominal capital return of 0.5% pa ##\left( =\dfrac{100.5-100}{100} \right)##.

(c) Nominal total return of 1.5% pa ##\left( =\dfrac{100.5-100+1}{100} \right)##.

(d) Real income return of 0.9708738% pa##\left( =\dfrac{ 1/(1+0.03)^1}{100} \right)##.

(e) Real capital return of 0.4854369% pa ##\left( =\dfrac{ (100.5-100)/(1+0.03)^1}{100} \right) ##.

Question 503  DDM, NPV, stock pricing

A share currently worth $100 is expected to pay a constant dividend of $4 for the next 5 years with the first dividend in one year (t=1) and the last in 5 years (t=5).

The total required return is 10% pa.

What do you expected the share price to be in 5 years, just after the dividend at that time has been paid?

(a) $100

(b) $115.16

(c) $136.63

(d) $161.05

(e) $185.47

Question 146  APR, effective rate

A three year corporate bond yields 12% pa with a coupon rate of 10% pa, paid semi-annually.

Find the effective six month yield, effective annual yield and the effective daily yield. Assume that each month has 30 days and that there are 360 days in a year.

All answers are given in the same order:

##r_\text{eff semi-annual}##, ##r_\text{eff yearly}##, ##r_\text{eff daily}##.

(a) 0.06, 0.1236, 0.000324.

(b) 0.058301, 0.12, 0.000315.

(c) 0.05, 0.1025, 0.000271.

(d) 0.05, 0.1, 0.000278.

(e) 0.048809, 0.1, 0.000265.

Question 269  time calculation, APR

A student won $1m in a lottery. Currently the money is in a bank account which pays interest at 6% pa, given as an APR compounding per month.

She plans to spend $20,000 at the beginning of every month from now on (so the first withdrawal will be at t=0). After each withdrawal, she will check how much money is left in the account. When there is less than $500,000 left, she will donate that remaining amount to charity.

In how many months will she make her last withdrawal and donate the remainder to charity?

(a) In 31 months (t=31 months).

(b) In 30 months (t=30 months).

(c) In 28 months (t=28 months).

(d) In 27 months (t=27 months).

(e) In 26 months (t=26 months).

Question 453  DDM, income and capital returns

The perpetuity with growth equation is:

###P_0=\dfrac{C_1}{r-g}###

Which of the following is NOT equal to the expected capital return as an effective annual rate?

(a) ##g##

(b) ##r+\dfrac{C_1}{P_0}##

(c) ##\dfrac{C_2}{C_1} -1##

(d) ##\dfrac{C_3-C_2}{C_2} ##

(e) ##\left( \dfrac{P_5}{P_3} \right)^{1/2}-1##

Question 350  CFFA

Find Sidebar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Sidebar Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	405
COGS	100
Depreciation	34
Rent expense	22
Interest expense	39
Taxable Income	210
Taxes at 30%	63
Net income	147

Sidebar Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Cash	0	0
Inventory	70	50
Trade debtors	11	16
Rent paid in advance	4	3
PPE	700	680
Total assets	785	749
Trade creditors	11	19
Bond liabilities	400	390
Contributed equity	220	220
Retained profits	154	120
Total L and OE	785	749

 

Note: All figures are given in millions of dollars ($m).

The cash flow from assets was:

(a) $138m

(b) $142m

(c) $143m

(d) $172m

(e) $176m

Question 512  capital budgeting, CFFA

Find the cash flow from assets (CFFA) of the following project.

Project Data
Project life	2 years
Initial investment in equipment	$6m
Depreciation of equipment per year for tax purposes	$1m
Unit sales per year	4m
Sale price per unit	$8
Variable cost per unit	$3
Fixed costs per year, paid at the end of each year	$1.5m
Tax rate	30%

Note 1: The equipment will have a book value of $4m at the end of the project for tax purposes. However, the equipment is expected to fetch $0.9 million when it is sold at t=2.

Note 2: Due to the project, the firm will have to purchase $0.8m of inventory initially, which it will sell at t=1. The firm will buy another $0.8m at t=1 and sell it all again at t=2 with zero inventory left. The project will have no effect on the firm's current liabilities.

Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).

(a) -6,   12.25,   16.68

(b) -6.8,   13.25,   14.05

(c) -6.8,   13.25,   15.88

(d) -6.8,   13.25,   18.51

(e) -6.8,   13.25,   17.71

Question 186  DDM, income and capital returns

Here's the Dividend Discount Model, used to price stocks:

### p_0=\frac{d_1}{r-g} ###

All rates are effective annual rates and the cash flows (##d_1##) are received every year. Note that the r and g terms in the above DDM could also be labelled: ###r = r_{\text{total, 0}\rightarrow\text{1yr, eff 1yr}}### ###g = r_{\text{capital, 0}\rightarrow\text{1yr, eff 1yr}}### Which of the following statements is NOT correct?

(a) The expected dividend in 3 years will be: ##d_3 = d_1 (1+g)^2##.

(b) The expected price in 3 years will be: ##p_3 = p_0 (1+g)^3##.

(c) The expected effective 3 year total return measured over 3 years is equal to: ##r_{\text{total, 0}\rightarrow\text{3yr, eff 3yr}} = (1+r)^3-1##.

(d) The expected effective 3 year total return measured over 3 years will be: ##r_{\text{total, 0}\rightarrow\text{3yr, eff 3yr}} = \dfrac{p_3-p_0+d_3}{p_0}##.

(e) The expected effective annual dividend yield will be: ##r_{\text{dividend, 0}\rightarrow\text{3yr, eff annual}} = \dfrac{d_1}{p_0}##.

Question 455  income and capital returns, payout policy, DDM, market efficiency

A fairly priced unlevered firm plans to pay a dividend of $1 next year (t=1) which is expected to grow by 3% pa every year after that. The firm's required return on equity is 8% pa.

The firm is thinking about reducing its future dividend payments by 10% so that it can use the extra cash to invest in more projects which are expected to return 8% pa, and have the same risk as the existing projects. Therefore, next year's dividend will be $0.90. No new equity or debt will be issued to fund the new projects, they'll all be funded by the cut in dividends.

What will be the stock's new annual capital return (proportional increase in price per year) if the change in payout policy goes ahead?

Assume that payout policy is irrelevant to firm value (so there's no signalling effects) and that all rates are effective annual rates.

(a) 2.7% pa.

(b) 3.0% pa.

(c) 3.5% pa.

(d) 3.3% pa.

(e) 3.8% pa.

Question 346  NPV, annuity due

Your poor friend asks to borrow some money from you. He would like $1,000 now (t=0) and every year for the next 5 years, so there will be 6 payments of $1,000 from t=0 to t=5 inclusive. In return he will pay you $10,000 in seven years from now (t=7).

What is the net present value (NPV) of lending to your friend?

Assume that your friend will definitely pay you back so the loan is risk-free, and that the yield on risk-free government debt is 10% pa, given as an effective annual rate.

(a) $1,340.7944

(b) $1,172.2533

(c) $776.3205

(d) $705.7459

(e) $340.7944

Question 25  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

A European company just issued two bonds, a

• 2 year zero coupon bond at a yield of 8% pa, and a
• 3 year zero coupon bond at a yield of 10% pa.

What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.

(a) 0.0374

(b) 0.0604

(c) 0.1204

(d) 0.1250

(e) 0.1411

Question 96  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

An Australian company just issued two bonds paying semi-annual coupons:

• 1 year zero coupon bond at a yield of 8% pa, and a
• 2 year zero coupon bond at a yield of 10% pa.

What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

(a) 6.01%

(b) 6.02%

(c) 9.20%

(d) 12.02%

(e) 18.40%

Question 624  franking credit, personal tax on dividends, imputation tax system, no explanation

Which of the following statements about Australian franking credits is NOT correct? Franking credits:

(a) Refund the corporate tax paid by companies to their individual shareholders. Therefore they prevent the double-taxation of dividends at the corporate and personal level.

(b) Are distributed to shareholders together with cash dividends.

(c) Are also called imputation credits.

(d) Are worthless to individuals who earn less than the tax-free threshold because they have a zero marginal personal tax rate.

(e) Are worthless to individual shareholders who are foreigners for tax purposes.

Question 206  CFFA, interest expense, interest tax shield

Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').

How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:

Annual interest expense is equal to:

(a) the bond's face value multiplied by its annual yield to maturity.

(b) the bond's face value multiplied by its annual coupon rate.

(c) the bond's market price at the start of the year multiplied by its annual yield to maturity.

(d) the bond's market price at the start of the year multiplied by its annual coupon rate.

(e) the future value of the actual cash payments of the bond over the year, grown to the end of the year, and grown by the bond's yield to maturity.

Question 68  WACC, CFFA, capital budgeting

A manufacturing company is considering a new project in the more risky services industry. The cash flows from assets (CFFA) are estimated for the new project, with interest expense excluded from the calculations. To get the levered value of the project, what should these unlevered cash flows be discounted by?

Assume that the manufacturing firm has a target debt-to-assets ratio that it sticks to.

(a) The manufacturing firm's before-tax WACC.

(b) The manufacturing firm's after-tax WACC.

(c) A services firm's before-tax WACC, assuming that the services firm has the same debt-to-assets ratio as the manufacturing firm.

(d) A services firm's after-tax WACC, assuming that the services firm has the same debt-to-assets ratio as the manufacturing firm.

(e) The services firm's levered cost of equity.

Question 371  interest tax shield, CFFA

One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:

###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###

Does this annual FFCF with zero interest expense or the annual interest tax shield?

Question 361  CFFA

Over the next year, the management of an unlevered company plans to:

• Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
• Pay dividends of $1m.
• Complete a $1.3m share buy-back.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2m

(b) $1m

(c) $0.4m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 226  CFFA

Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

World Bar
Income Statement for
year ending 30th June 2013
	$m
Sales	300
COGS	150
Operating expense	50
Depreciation	40
Interest expense	10
Taxable income	50
Tax at 30%	15
Net income	35

World Bar
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	200	230
PPE
Cost	400	400
Accumul. depr.	75	35
Carrying amount	325	365
Total assets	525	595
Liabilities
Current liabilities	150	205
Non-current liabilities	235	250
Owners' equity
Retained earnings	100	100
Contributed equity	40	40
Total L and OE	525	595

 

Note: all figures above and below are given in millions of dollars ($m).

(a) 145

(b) 100

(c) 90

(d) 60

(e) -20

Question 291  CFFA

Find Scubar Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Scubar Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	200
COGS	60
Depreciation	20
Rent expense	11
Interest expense	19
Taxable Income	90
Taxes at 30%	27
Net income	63

Scubar Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Inventory	60	50
Trade debtors	19	6
Rent paid in advance	3	2
PPE	420	400
Total assets	502	458
Trade creditors	10	8
Bond liabilities	200	190
Contributed equity	130	130
Retained profits	162	130
Total L and OE	502	458

 

Note: All figures are given in millions of dollars ($m).

The cash flow from assets was:

(a) $40m

(b) $41m

(c) $54m

(d) $60m

(e) $74m

Question 370  capital budgeting, NPV, interest tax shield, WACC, CFFA

Project Data
Project life	2 yrs
Initial investment in equipment	$600k
Depreciation of equipment per year	$250k
Expected sale price of equipment at end of project	$200k
Revenue per job	$12k
Variable cost per job	$4k
Quantity of jobs per year	120
Fixed costs per year, paid at the end of each year	$100k
Interest expense in first year (at t=1)	$16.091k
Interest expense in second year (at t=2)	$9.711k
Tax rate	30%
Government treasury bond yield	5%
Bank loan debt yield	6%
Levered cost of equity	12.5%
Market portfolio return	10%
Beta of assets	1.24
Beta of levered equity	1.5
Firm's and project's debt-to-equity ratio	25%

Notes

1. The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.

Assumptions

• The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
• Thousands are represented by 'k' (kilo).
• All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
• All rates and cash flows are nominal. The inflation rate is 2% pa.
• All rates are given as effective annual rates.
• The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.

What is the net present value (NPV) of the project?

(a) $684.222k

(b) $690.919k

(c) $697.616k

(d) $698.713k

(e) $710.601k

Question 337  capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model

A fast-growing firm is suitable for valuation using a multi-stage growth model.

It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:

• 12% pa for the next two years (from t=1 to 3),
• 5% over the fourth year (from t=3 to 4), and
• -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.

Assume that:

• The nominal WACC after tax is 9.5% pa and is not expected to change.
• The nominal WACC before tax is 10% pa and is not expected to change.
• The firm has a target debt-to-equity ratio that it plans to maintain.
• The inflation rate is 3% pa.
• All rates are given as nominal effective annual rates.

What is the levered value of this fast growing firm's assets?

(a) $13.19m

(b) $12.36m

(c) $11.77m

(d) $11.53m

(e) $11.20m

Question 75  WACC, CAPM

A company has:

• 50 million shares outstanding.
• The market price of one share is currently $6.
• The risk-free rate is 5% and the market return is 10%.
• Market analysts believe that the company's ordinary shares have a beta of 2.
• The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
• The company's debentures are publicly traded and their market price is equal to 90% of their face value.
• The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.

What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.

(a) 11.75%

(b) 11.82%

(c) 13.54%

(d) 13.78%

(e) 20.84%

Question 237  WACC, Miller and Modigliani, interest tax shield

Which of the following discount rates should be the highest for a levered company? Ignore the costs of financial distress.

(a) Cost of debt (##r_\text{D}##).

(b) Unlevered cost of equity (##r_\text{E, U}##).

(c) Levered cost of equity (##r_\text{E, L}##).

(d) Levered before-tax WACC (##r_\text{V, LxITS}##).

(e) Levered after-tax WACC (##r_\text{V, LwITS}##).

Question 738  financial statement, balance sheet, income statement

Where can a private firm's market value of equity be found? It can be sourced from the company's:

(a) Income statement

(b) Balance sheet

(c) Cash flow statement

(d) Stock exchange data.

(e) It's not published, it can only be estimated using multiples or discounted cash flow methods.

Question 749  Multiples valuation, PE ratio, price to revenue ratio, price to book ratio, NPV

A real estate agent says that the price of a house in Sydney Australia is approximately equal to the gross weekly rent times 1000.

What type of valuation method is the real estate agent using?

(a) Price to EBITDA multiple.

(b) Price to book multiple.

(c) Price to earnings multiple.

(d) Price to revenue multiple.

(e) Discounted cash flow (DCF).

Question 760  time calculation, interest only loan, no explanation

Five years ago (##t=-5## years) you entered into an interest-only home loan with a principal of $500,000, an interest rate of 4.5% pa compounding monthly with a term of 25 years.

Then interest rates suddenly fall to 3% pa (##t=0##), but you continue to pay the same monthly home loan payments as you did before. Will your home loan be paid off by the end of its remaining term? If so, in how many years from now? Measure the time taken to pay off the home loan from the current time which is 5 years after the home loan was first entered into.

Assume that the lower interest rate was given to you immediately after the loan repayment at the end of year 5, which was the 60th payment since the loan was granted. Also assume that rates were and are expected to remain constant.

(a) Yes, in 117 months, which is 9 years and 9 months.

(b) Yes, in 152 months, which is 12 years and 8 months.

(c) Yes, in 202 months, which is 16 years and 10 months.

(d) Yes, in 240 months, which is 20 years.

(e) No, it will take longer than 20 years to pay off the loan.

Question 762  equivalent annual cash flow, no explanation

Radio-Rentals.com offers the Apple iphone 5S smart phone for rent at $12.95 per week paid in advance on a 2 year contract. After renting the phone, you must return it to Radio-Rentals.

Kogan.com offers the Apple iphone 5S smart phone for sale at $699. You estimate that the phone will last for 3 years before it will break and be worthless.

Currently, the effective annual interest rate is 11.351%, the effective monthly interest rate 0.9% and the effective weekly interest rate is 0.207%. Assume that there are exactly 52 weeks per year and 12 months per year.

Find the equivalent annual cost of renting the phone and also buying the phone. The answers below are listed in the same order.

(a) $362.33,   $287.79

(b) $362.33,   $506.29

(c) $516.29,   $506.29

(d) $673.40,   $233.00

(e) $711.67,   $287.79

Question 403  PE ratio, no explanation

Which of the following investable assets is the LEAST suitable for valuation using PE multiples techniques?

(a) Common equity in a small private company.

(b) Common equity in a listed public company.

(c) Commercial real estate.

(d) Ten year commercial real estate lease.

(e) Residential real estate.

Question 493  PE ratio

A firm has 2m shares and a market capitalisation of equity of $30m. The firm just announced earnings of $5m and paid an annual dividend of $0.75 per share.

What is the firm's (backward looking) price/earnings (PE) ratio?

(a) 2.5

(b) 3

(c) 6

(d) 15

(e) 20

Question 620  bond pricing, income and capital returns

Let the 'income return' of a bond be the coupon at the end of the period divided by the market price now at the start of the period ##(C_1/P_0)##. The expected income return of a premium fixed coupon bond is:

(a) Less than its expected total return.

(b) Equal to its expected total return.

(c) More than its expected total return.

(d) More than its coupon rate.

(e) Equal to its coupon rate.

Question 254  time calculation, APR

Your main expense is fuel for your car which costs $100 per month. You just refueled, so you won't need any more fuel for another month (first payment at t=1 month).

You have $2,500 in a bank account which pays interest at a rate of 6% pa, payable monthly. Interest rates are not expected to change.

Assuming that you have no income, in how many months time will you not have enough money to fully refuel your car?

(a) In 23 months (t=23 months).

(b) In 24 months (t=24 months).

(c) In 25 months (t=25 months).

(d) In 26 months (t=26 months).

(e) In 27 months (t=27 months).

Question 609  debt terminology

You deposit cash into your bank account. Have you or debt?

Question 351  CFFA

Over the next year, the management of an unlevered company plans to:

• Achieve firm free cash flow (FFCF or CFFA) of $1m.
• Pay dividends of $1.8m
• Complete a $1.3m share buy-back.
• Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2.1m

(b) $1.3m

(c) $0.8m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 273  CFFA, capital budgeting

Value the following business project to manufacture a new product.

Project Data
Project life	2 yrs
Initial investment in equipment	$6m
Depreciation of equipment per year	$3m
Expected sale price of equipment at end of project	$0.6m
Unit sales per year	4m
Sale price per unit	$8
Variable cost per unit	$5
Fixed costs per year, paid at the end of each year	$1m
Interest expense per year	0
Tax rate	30%
Weighted average cost of capital after tax per annum	10%

Notes

1. The firm's current assets and current liabilities are $3m and $2m respectively right now. This net working capital will not be used in this project, it will be used in other unrelated projects.
   Due to the project, current assets (mostly inventory) will grow by $2m initially (at t = 0), and then by $0.2m at the end of the first year (t=1).
   Current liabilities (mostly trade creditors) will increase by $0.1m at the end of the first year (t=1).
   At the end of the project, the net working capital accumulated due to the project can be sold for the same price that it was bought.
2. The project cost $0.5m to research which was incurred one year ago.

Assumptions

• All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
• All rates and cash flows are real. The inflation rate is 3% pa.
• All rates are given as effective annual rates.
• The business considering the project is run as a 'sole tradership' (run by an individual without a company) and is therefore eligible for a 50% capital gains tax discount when the equipment is sold, as permitted by the Australian Tax Office.

What is the expected net present value (NPV) of the project?

(a) $5.2m

(b) $8.481735m

(c) $8.743802m

(d) $8.991736m

(e) $9.719008m

Question 343  CFFA, capital budgeting

An old company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.

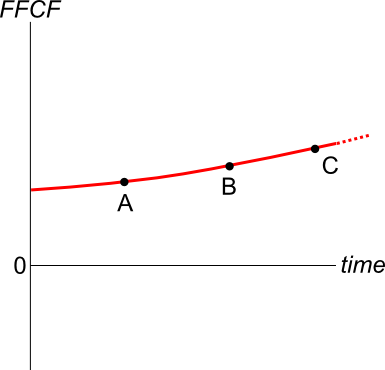
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:

###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###

Which point corresponds to the best time to calculate the terminal value?

(a) Point A.

(b) Point B.

(c) Point C.

(d) Any of the points.

(e) None of the points.

Question 360  CFFA

Find Ching-A-Lings Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Ching-A-Lings Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	100
COGS	20
Depreciation	20
Rent expense	11
Interest expense	19
Taxable Income	30
Taxes at 30%	9
Net income	21

Ching-A-Lings Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Inventory	49	38
Trade debtors	14	2
Rent paid in advance	5	5
PPE	400	400
Total assets	468	445
Trade creditors	4	10
Bond liabilities	200	190
Contributed equity	145	145
Retained profits	119	100
Total L and OE	468	445

 

Note: All figures are given in millions of dollars ($m).

The cash flow from assets was:

(a) $43m

(b) $31m

(c) $23m

(d) $11m

(e) $1m

Question 224  CFFA

Cash Flow From Assets (CFFA) can be defined as:

(a) Cash available to distribute to creditors and stockholders.

(b) Cash flow to creditors minus cash flow to stockholders.

(c) Net income (or earnings) plus depreciation plus interest expense.

(d) Net income minus the increase in net working capital.

(e) Net income minus net capital spending minus the increase in net working capital.

Question 559  variance, standard deviation, covariance, correlation

Which of the following statements about standard statistical mathematics notation is NOT correct?

(a) The arithmetic average of variable X is represented by ##\bar{X}##.

(b) The standard deviation of variable X is represented by ##\sigma_X##.

(c) The variance of variable X is represented by ##\sigma_X^2##.

(d) The covariance between variables X and Y is represented by ##\sigma_{X,Y}^2##.

(e) The correlation between variables X and Y is represented by ##\rho_{X,Y}##.

Question 635  continuously compounding rate

A $100 stock has a continuously compounded expected total return of 10% pa. Its dividend yield is 2% pa with continuous compounding. What do you expect its price to be in 2.5 years?

(a) $134.985881

(b) $128.402542

(c) $126.905871

(d) $122.140276

(e) $121.215844

Question 191  NPV, IRR, profitability index, pay back period

A project's Profitability Index (PI) is less than 1. Select the most correct statement:

(a) The project should be rejected.

(b) The project's IRR is more than its required return.

(c) The project's payback period will be less than 3 years.

(d) The project's IRR is equal to its required return.

(e) The project's NPV is greater than 1.

Question 140  IRR, NPV, profitability index

A project has an internal rate of return (IRR) which is greater than its required return. Select the most correct statement.

(a) The NPV will be negative and the profitability index will be less than 1.

(b) The NPV will be positive and the profitability index will be more than 1.

(c) The payback period will be positive and the Accounting Rate of Return will be more than the target return.

(d) The NPV will be positive and the profitability index will be negative.

(e) The NPV will be negative and the profitability index will be positive.

Question 700  utility, risk aversion, utility function, gamble

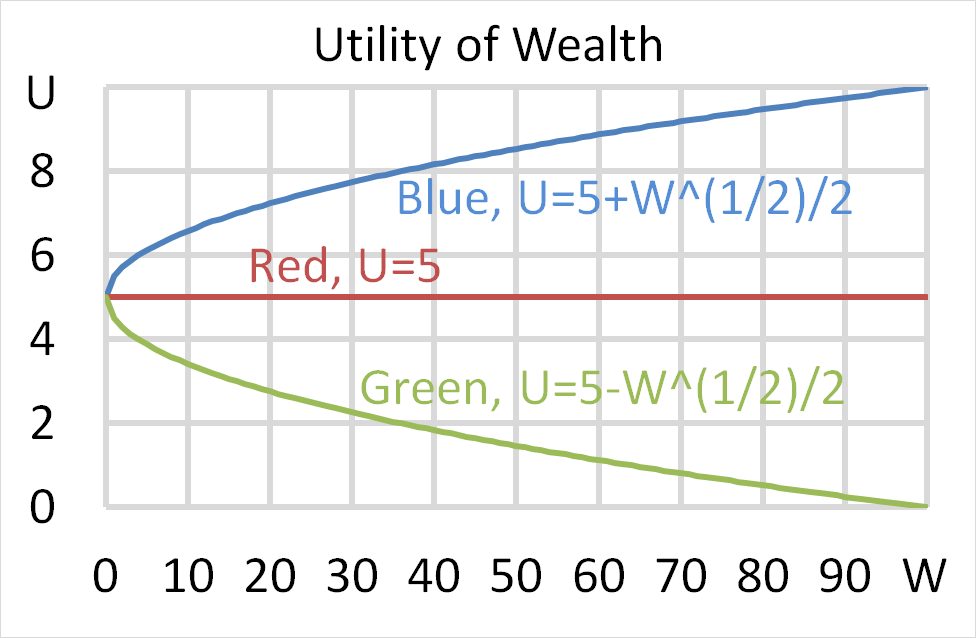
Mr Blue, Miss Red and Mrs Green are people with different utility functions.

Each person has $50 of initial wealth. A coin toss game is offered to each person at a casino where the player can win or lose $50. Each player can flip a coin and if they flip heads, they receive $50. If they flip tails then they will lose $50. Which of the following statements is NOT correct?

(a) Mr Blue's expected utility of wealth from gambling is 7.5 while refusing is 8.54. So the gamble makes him less happy.

(b) Miss Red's expected utility of wealth from gambling is 5 and refusing is also 5. So the gamble doesn't affect her happiness at all.

(c) Mr Blue's certainty equivalent of the risky gamble is $25. This is less than his current wealth which is why he would refuse.

(d) Miss Red's certainty equivalent of the risky gamble is any wealth. She's indifferent since she always has the same level of happiness.

(e) Mrs Green's certainty equivalent of the risky gamble is $25. This is less than her current wealth which is why she would refuse.

Question 306  risk, standard deviation

Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.

What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?

Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.

(a) ##\sigma_\text{yearly} = \sigma_\text{monthly}##

(b) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times 12##

(c) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times 144##

(d) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times \sqrt{12}##

(e) ##\sigma_\text{yearly} = \sigma_\text{monthly} \times {12}^{1/3}##

Question 339  bond pricing, inflation, market efficiency, income and capital returns

Economic statistics released this morning were a surprise: they show a strong chance of consumer price inflation (CPI) reaching 5% pa over the next 2 years.

This is much higher than the previous forecast of 3% pa.

A vanilla fixed-coupon 2-year risk-free government bond was issued at par this morning, just before the economic news was released.

What is the expected change in bond price after the economic news this morning, and in the next 2 years? Assume that:

• Inflation remains at 5% over the next 2 years.
• Investors demand a constant real bond yield.
• The bond price falls by the (after-tax) value of the coupon the night before the ex-coupon date, as in real life.

(a) Today the price would have increased significantly.
Over the next 2 years, the bond price is expected to increase, measured on each ex-coupon date.

(b) Today the price would have increased significantly.
Over the next 2 years, the bond price is expected to be unchanged, measured on each ex-coupon date.

(c) Today the price would have been unchanged.
Over the next 2 years, the bond price is expected to increase, measured on each ex-coupon date.

(d) Today the price would have decreased significantly.
Over the next 2 years, the bond price is expected to increase, measured on each ex-coupon date.

(e) Today the price would have decreased significantly.
Over the next 2 years, the bond price is expected to be unchanged, measured on each ex-coupon date.

Question 119  market efficiency, fundamental analysis, joint hypothesis problem

Your friend claims that by reading 'The Economist' magazine's economic news articles, she can identify shares that will have positive abnormal expected returns over the next 2 years. Assuming that her claim is true, which statement(s) are correct?

(i) Weak form market efficiency is broken.

(ii) Semi-strong form market efficiency is broken.

(iii) Strong form market efficiency is broken.

(iv) The asset pricing model used to measure the abnormal returns (such as the CAPM) is either wrong (mis-specification error) or is measured using the wrong inputs (data errors) so the returns may not be abnormal but rather fair for the level of risk.

Select the most correct response:

(a) Only (iii) is true.

(b) Only (ii) and (iii) are true.

(c) Only (i), (ii) and (iii) are true.

(d) Either (ii) and (iii) are true, or (iv) is true, or (ii), (iii) and (iv) are true.

(e) Either (i), (ii) and (iii) are true, or (iv) is true, or all are true.

Question 338  market efficiency, CAPM, opportunity cost, technical analysis

A man inherits $500,000 worth of shares.

He believes that by learning the secrets of trading, keeping up with the financial news and doing complex trend analysis with charts that he can quit his job and become a self-employed day trader in the equities markets.

What is the expected gain from doing this over the first year? Measure the net gain in wealth received at the end of this first year due to the decision to become a day trader. Assume the following:

• He earns $60,000 pa in his current job, paid in a lump sum at the end of each year.
• He enjoys examining share price graphs and day trading just as much as he enjoys his current job.
• Stock markets are weak form and semi-strong form efficient.
• He has no inside information.
• He makes 1 trade every day and there are 250 trading days in the year. Trading costs are $20 per trade. His broker invoices him for the trading costs at the end of the year.
• The shares that he currently owns and the shares that he intends to trade have the same level of systematic risk as the market portfolio.
• The market portfolio's expected return is 10% pa.

Measure the net gain over the first year as an expected wealth increase at the end of the year.

(a) $110,000

(b) $50,000

(c) $45,000

(d) -$15,000

(e) -$65,000

Question 242  technical analysis, market efficiency

Select the most correct statement from the following.

'Chartists', also known as 'technical traders', believe that:

(a) Markets are weak-form efficient.

(b) Markets are semi-strong-form efficient.

(c) Past prices cannot be used to predict future prices.

(d) Past returns can be used to predict future returns.

(e) Stock prices reflect all publically available information.

Question 340  market efficiency, opportunity cost

A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.

This fee is charged regardless of whether the fund makes gains or losses on your money.

The fund offers to invest your money in shares which have an expected return of 10% pa before fees.

You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.

What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:

• The fund has no private information.
• Markets are weak and semi-strong form efficient.
• The fund's transaction costs are negligible.
• The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.

(a) $0

(b) -$20,000.00

(c) -$48,000.17

(d) -$51,999.83

(e) -$80,000.00

Question 417  NPV, market efficiency, DDM

A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the end-of-year amount, paid at the end of every year.

This fee is charged regardless of whether the fund makes gains or losses on your money.

The fund offers to invest your money in shares which have an expected return of 10% pa before fees.

You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.

How much money do you expect to have in the fund in 40 years? Also, what is the future value of the fees that the fund expects to earn from you? Give both amounts as future values in 40 years. Assume that:

• The fund has no private information.
• Markets are weak and semi-strong form efficient.
• The fund's transaction costs are negligible.
• The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
• The fund invests its fees in the same companies as it invests your funds in, but with no fees.

The below answer choices list your expected wealth in 40 years and then the fund's expected wealth in 40 years.

(a) $4,462,125.27, $63,800.29

(b) $3,407,788.62, $1,118,136.94

(c) $3,316,736.53, $1,209,189.03

(d) $2,172,452.15, $2,353,473.41

(e) $2,017,206.85, $2,508,718.71

Question 673  CAPM, beta, expected and historical returns

A stock has a beta of 1.5. The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.

In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 1%. The risk free rate was unchanged.

What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?

(a) -12.5%

(b) -4%

(c) -1.5%

(d) -1%

(e) 12.5%

Question 380  leverage, capital structure

The "interest expense" on a company's annual income statement is equal to the cash interest payments (but not principal payments) made to debt holders during the year. or ?

Question 397  financial distress, leverage, capital structure, NPV

A levered firm has a market value of assets of $10m. Its debt is all comprised of zero-coupon bonds which mature in one year and have a combined face value of $9.9m.

Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.

Therefore the current market capitalisation of debt ##(D_0)## is $9m and equity ##(E_0)## is $1m.

A new project presents itself which requires an investment of $2m and will provide a:

• $6.6m cash flow with probability 0.5 in the good state of the world, and a
• -$4.4m (notice the negative sign) cash flow with probability 0.5 in the bad state of the world.

The project can be funded using the company's excess cash, no debt or equity raisings are required.

What would be the new market capitalisation of equity ##(E_\text{0, with project})## if shareholders vote to proceed with the project, and therefore should shareholders proceed with the project?

(a) $2.5m, so they should vote yes.

(b) $2.045455m, so they should vote yes.

(c) $0.9m, so they should vote no.

(d) $0, so they should vote no.

(e) -$0.9m, so they should vote no.

Question 305  option, short selling, speculation

You believe that the price of a share will fall significantly very soon, but the rest of the market does not. The market thinks that the share price will remain the same. Assuming that your prediction will soon be true, which of the following trades is a bad idea? In other words, which trade will NOT make money or prevent losses?

(a) Sell all existing stock that you own.

(b) Short sell the stock.

(c) Buy put options on the stock.

(d) Sell put options on the stock.

(e) Sell call options on the stock.

Question 312  foreign exchange rate, American and European terms

If the current AUD exchange rate is USD 0.9686 = AUD 1, what is the American terms quote of the AUD against the USD?

(a) 0.9686 USD per AUD

(b) 0.9686 AUD per USD

(c) 1.0324 USD per AUD

(d) 1.0324 AUD per USD

(e) 1.0324 AUD per 2 USD

Question 313  foreign exchange rate, American and European terms

If the AUD appreciates against the USD, the American terms quote of the AUD will or ?

Question 245  foreign exchange rate, monetary policy, foreign exchange rate direct quote, no explanation

Investors expect Australia's central bank, the RBA, to leave the policy rate unchanged at their next meeting.

Then unexpectedly, the policy rate is reduced due to fears that Australia's GDP growth is slowing.

What do you expect to happen to Australia's exchange rate? Direct and indirect quotes are given from the perspective of an Australian.

The Australian dollar will:

(a) Appreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will increase.

(b) Depreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will decrease.

(c) Appreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will decrease.

(d) Depreciate against the USD, so the 'direct quote' of the AUD (AUD per USD) will increase.

(e) Depreciate against the USD, so the 'indirect quote' of the AUD (USD per AUD) will increase.

Question 283  portfolio risk, correlation, needs refinement

Three important classes of investable risky assets are:

• Corporate debt which has low total risk,
• Real estate which has medium total risk,
• Equity which has high total risk.

Assume that the correlation between total returns on:

• Corporate debt and real estate is 0.1,
• Corporate debt and equity is 0.1,
• Real estate and equity is 0.5.

You are considering investing all of your wealth in one or more of these asset classes. Which portfolio will give the lowest total risk? You are restricted from shorting any of these assets. Disregard returns and the risk-return trade-off, pretend that you are only concerned with minimising risk.

(a) Most money in corporate debt, with some money in equity and real estate.

(b) Most money in equity, with some money in corporate debt and real estate.

(c) Most money in real estate, with some money in corporate debt and equity.

(d) Most money in corporate debt, with some money in real estate and none in equity.

(e) All money in corporate debt.

Question 450  CAPM, risk, portfolio risk, no explanation

The accounting identity states that the book value of a company's assets (A) equals its liabilities (L) plus owners equity (OE), so A = L + OE.

The finance version states that the market value of a company's assets (V) equals the market value of its debt (D) plus equity (E), so V = D + E.

Therefore a business's assets can be seen as a portfolio of the debt and equity that fund the assets.

Let ##\sigma_\text{V total}^2## be the total variance of returns on assets, ##\sigma_\text{V syst}^2## be the systematic variance of returns on assets, and ##\sigma_\text{V idio}^2## be the idiosyncratic variance of returns on assets, and ##\rho_\text{D idio, E idio}## be the correlation between the idiosyncratic returns on debt and equity.

Which of the following equations is NOT correct?

(a) ##r_V = \dfrac{D}{V}.r_D + \dfrac{E}{V}.r_E##

(b) ##\beta_V = \dfrac{D}{V}.\beta_D + \dfrac{E}{V}.\beta_E##

(c) ##\sigma_\text{V syst}^2 = \left(\dfrac{D}{V}\right)^2.\sigma_\text{D syst}^2 + \left(\dfrac{E}{V}\right)^2.\sigma_\text{E syst}^2##

(d) ##\sigma_\text{V idio}^2 = \left(\dfrac{D}{V}\right)^2.\sigma_\text{D idio}^2 + \left(\dfrac{E}{V}\right)^2.\sigma_\text{E idio}^2 + 2.\dfrac{D}{V}.\dfrac{E}{V}.\rho_\text{D idio, E idio}.\sigma_\text{D idio}.\sigma_\text{E idio}##

(e) ##\sigma_\text{V total}^2 = \left(\dfrac{D}{V}\right)^2.\sigma_\text{D total}^2 + \left(\dfrac{E}{V}\right)^2.\sigma_\text{E total}^2##

Question 594  future, continuously compounding rate

The current gold price is $700, gold storage costs are 2% pa and the risk free rate is 10% pa, both with continuous compounding.

What should be the 3 year gold futures price?

(a) $758.30

(b) $773.62

(c) $889.87

(d) $944.90

(e) $1,003.33

Question 722  mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate

Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?

Price and Return Population Statistics
Time	Prices	LGDR	GDR	NDR
0	100
1	50	-0.6931	0.5	-0.5
2	100	0.6931	2	1
Arithmetic average		0	1.25	0.25
Arithmetic standard deviation		0.9802	1.0607	1.0607

 

(a) The geometric average of the gross discrete returns (GAGDR) equals 1 which is 100%.

(b) ##\text{GAGDR} = \exp \left( \text{AALGDR} \right)##. The GAGDR is equal to the natural exponent of the arithmetic average of the logarithms of the gross discrete returns (AALGDR).

(c) ##\text{GAGDR} = \left( P_T/P_0 \right)^{1/T}##. The GAGDR equals the ratio of the last and first prices raised to the power of the inverse of the number of time periods between them.

(d) ##\text{LGAGDR} = \text{AALGDR}##. This is always true, regardless of the distribution of the prices or returns and the number of return observations. The logarithm of the geometric average of the gross discrete returns (LGAGDR) is always equal to the arithmetic average of the logarithms of the gross discrete returns (AALGDR).

(e) ##\text{LAAGDR} = \text{AALGDR} + \text{SDLGDR}^2/2##. This is always true, regardless of the distribution of the prices or returns and the number of return observations. The logarithm of the arithmetic average of the gross discrete returns (LAAGDR) equals the arithmetic average of the logarithms of the gross discrete returns (AALGDR) plus half the variance of the LGDR's.

Question 723  mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate

Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?

Price and Return Population Statistics
Time	Prices	LGDR	GDR	NDR
0	100
1	99	-0.010050	0.990000	-0.010000
2	180.40	0.600057	1.822222	0.822222
3	112.73	0.470181	0.624889	0.375111
Arithmetic average		0.0399	1.1457	0.1457
Arithmetic standard deviation		0.4384	0.5011	0.5011

 

(a) The geometric average of the gross discrete returns (GAGDR) equals 1.04075 which is 104.075%.

(b) ##\exp \left( \text{GAGDR} \right) = \text{AALGDR}##. The natural exponent of the GAGDR equals the arithmetic average of the logarithms of the gross discrete returns (AALGDR).

(c) ##\text{GAGDR}^T = \left( P_T/P_0 \right)##. The GAGDR raised to the power of the number of time period that it's measured over equals the ratio of the first and last prices.

(d) ##\text{GAGDR} = \exp \left( \text{AALGDR} \right)##. This is always true, regardless of the distribution of the prices or returns. The logarithm of the geometric average of the gross discrete returns (LGAGDR) is always equal to the arithmetic average of the logarithm of the gross discrete returns (AALGDR).

(e) ##\text{AAGDR} \approx \exp \left( \text{AALGDR} + \text{SDLGDR}^2/2 \right)##. This is only approximately true and depends on the distribution of the prices and returns. It's asymptotically true as the time period that the returns are measured over reaches infinity.

Question 779  mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate

Fred owns some BHP shares. He has calculated BHP’s monthly returns for each month in the past 30 years using this formula:

###r_\text{t monthly}=\ln⁡ \left( \dfrac{P_t}{P_{t-1}} \right)###

He then took the arithmetic average and found it to be 0.8% per month using this formula:

###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.008=0.8\% \text{ per month}###

He also found the standard deviation of these monthly returns which was 15% per month:

###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.15=15\%\text{ per month}###

Assume that the past historical average return is the true population average of future expected returns and the stock's returns calculated above ##(r_\text{t monthly})## are normally distributed. Which of the below statements about Fred’s BHP shares is NOT correct?

(a) The returns ##r_\text{t monthly}## are continuously compounded monthly returns.

(b) The mean, median and mode of the continuously compounded annual return is expected to equal 0.8% per month.

(c) The annualised average continuously compounded return is ##\bar{r}_\text{cc annual}=12×0.008=0.096=9.6\%\text{ pa}##. The annualised standard deviation is ##\sigma_\text{annual} = \sqrt{12}×0.15=0.519615242 = 52\%\text{ pa}##.

(d) If the current price of the BHP shares is $20, they're expected to have a median value of $52.2339 ##(= 20×e^{0.008×12×10})## in 10 years.

(e) If the current price of the BHP shares is $20, they're expected to have a mean value of $13.5411 ##(= 20×e^{(0.008 - 0.15^2/2)×12×10})## in 10 years.

Question 95  interest tax shield

The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###

###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###

For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?

You may assume:

• the value of debt (D) is constant through time,
• The cost of debt and the yield on debt are equal and given by ##r_D##.
• the appropriate rate to discount interest tax shields is ##r_D##.
• ##\text{IntExp}=D.r_D##

(a) ##D.t_c##

(b) ##D.r_D/t_c ##

(c) ##D.r_D.(1-t_c)##

(d) ##D.r_D/(1-t_c)##

(e) ##D.r_D.(t_c-1)##

Question 772  interest tax shield, capital structure, leverage

A firm issues debt and uses the funds to buy back equity. Assume that there are no costs of financial distress or transactions costs. Which of the following statements about interest tax shields is NOT correct?

(a) Higher debt leads to higher interest expense.

(b) Higher interest expense leads to lower profit before tax, following on from above.

(c) Lower profit before tax leads to lower tax payments, following on from above.

(d) Lower tax payments lead to higher cash flow from assets, following on from above.

(e) Lower profit after tax leads to a lower share price, following on from above.