Total cash flows can be broken into income and capital cash flows. What is the name given to the income cash flow from owning shares?
An asset's total expected return over the next year is given by:
###r_\text{total} = \dfrac{c_1+p_1-p_0}{p_0} ###
Where ##p_0## is the current price, ##c_1## is the expected income in one year and ##p_1## is the expected price in one year. The total return can be split into the income return and the capital return.
Which of the following is the expected capital return?
Question 542 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to double every 10 years, what must be the expected future capital return, given as an effective annual rate?
Question 278 inflation, real and nominal returns and cash flows
Imagine that the interest rate on your savings account was 1% per year and inflation was 2% per year.
Question 993 inflation, real and nominal returns and cash flows
In February 2020, the RBA cash rate was 0.75% pa and the Australian CPI inflation rate was 1.8% pa.
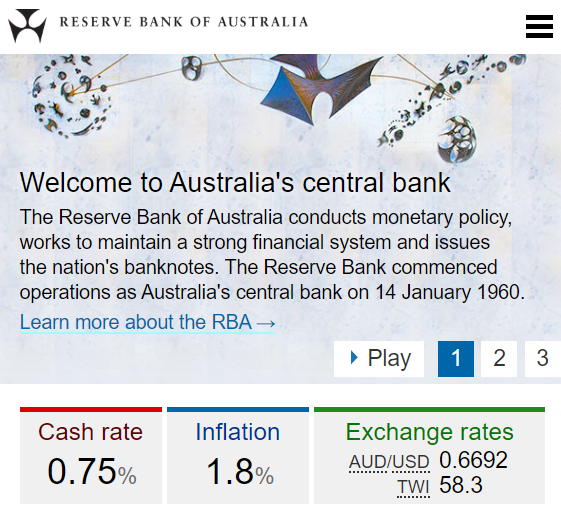
You currently have $100 in the bank which pays a 0.75% pa interest rate.
Apples currently cost $1 each at the shop and inflation is 1.8% pa which is the expected growth rate in the apple price.
This information is summarised in the table below, with some parts missing that correspond to the answer options. All rates are given as effective annual rates. Note that when payments are not specified as real, as in this question, they're conventionally assumed to be nominal.
| Wealth in Dollars and Apples | ||||
| Time (year) | Bank account wealth ($) | Apple price ($) | Wealth in apples | |
| 0 | 100 | 1 | 100 | |
| 1 | 100.75 | 1.018 | (a) | |
| 2 | (b) | (c) | (d) | |
Which of the following statements is NOT correct? Your:
Question 353 income and capital returns, inflation, real and nominal returns and cash flows, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.
Inflation is expected to be 2% pa. All rates are given as effective annual rates.
What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.
Question 525 income and capital returns, real and nominal returns and cash flows, inflation
Which of the following statements about cash in the form of notes and coins is NOT correct? Assume that inflation is positive.
Notes and coins:
Question 526 real and nominal returns and cash flows, inflation, no explanation
How can a nominal cash flow be precisely converted into a real cash flow?
Question 732 real and nominal returns and cash flows, inflation, income and capital returns
An investor bought a bond for $100 (at t=0) and one year later it paid its annual coupon of $1 (at t=1). Just after the coupon was paid, the bond price was $100.50 (at t=1). Inflation over the past year (from t=0 to t=1) was 3% pa, given as an effective annual rate.
Which of the following statements is NOT correct? The bond investment produced a:
You're considering making an investment in a particular company. They have preference shares, ordinary shares, senior debt and junior debt.
Which is the safest investment? Which has the highest expected returns?
Which business structure or structures have the advantage of limited liability for equity investors?
Question 531 bankruptcy or insolvency, capital structure, risk, limited liability
Who is most in danger of being personally bankrupt? Assume that all of their businesses' assets are highly liquid and can therefore be sold immediately.
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.
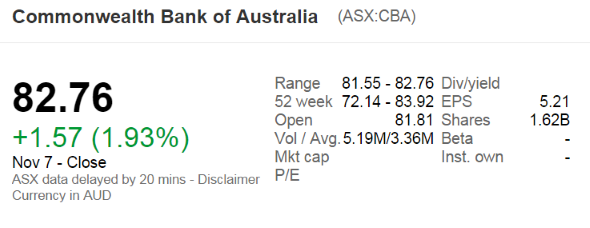
What was CBA's market capitalisation of equity?
Question 444 investment decision, corporate financial decision theory
The investment decision primarily affects which part of a business?
Question 445 financing decision, corporate financial decision theory
The financing decision primarily affects which part of a business?
Question 443 corporate financial decision theory, investment decision, financing decision, working capital decision, payout policy
Business people make lots of important decisions. Which of the following is the most important long term decision?
The expression 'you have to spend money to make money' relates to which business decision?
Katya offers to pay you $10 at the end of every year for the next 5 years (t=1,2,3,4,5) if you pay her $50 now (t=0). You can borrow and lend from the bank at an interest rate of 10% pa, given as an effective annual rate. Ignore credit risk.
This annuity formula ##\dfrac{C_1}{r}\left(1-\dfrac{1}{(1+r)^3} \right)## is equivalent to which of the following formulas? Note the 3.
In the below formulas, ##C_t## is a cash flow at time t. All of the cash flows are equal, but paid at different times.
Some countries' interest rates are so low that they're zero.
If interest rates are 0% pa and are expected to stay at that level for the foreseeable future, what is the most that you would be prepared to pay a bank now if it offered to pay you $10 at the end of every year for the next 5 years?
In other words, what is the present value of five $10 payments at time 1, 2, 3, 4 and 5 if interest rates are 0% pa?
There are many ways to write the ordinary annuity formula.
Which of the following is NOT equal to the ordinary annuity formula?
The following cash flows are expected:
- 10 yearly payments of $60, with the first payment in 3 years from now (first payment at t=3 and last at t=12).
- 1 payment of $400 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 58 NPV, inflation, real and nominal returns and cash flows, Annuity
A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.
After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.
The required return of the project is 21% pa given as an effective annual nominal rate.
All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.
The Net Present Value is:
The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###
What is ##g##? The value ##g## is the long term expected:
The first payment of a constant perpetual annual cash flow is received at time 5. Let this cash flow be ##C_5## and the required return be ##r##.
So there will be equal annual cash flows at time 5, 6, 7 and so on forever, and all of the cash flows will be equal so ##C_5 = C_6 = C_7 = ...##
When the perpetuity formula is used to value this stream of cash flows, it will give a value (V) at time:
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What would you call the expression ## C_1/P_0 ##?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###P_0=\frac{d_1}{r-g}###
A stock pays dividends annually. It just paid a dividend, but the next dividend (##d_1##) will be paid in one year.
According to the DDM, what is the correct formula for the expected price of the stock in 2.5 years?
In the dividend discount model:
###P_0 = \dfrac{C_1}{r-g}###
The return ##r## is supposed to be the:
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.
What is the price of the share now?
A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.00 | 1.05 | 1.10 | 1.15 | ... |
After year 4, the annual dividend will grow in perpetuity at 5% pa, so;
- the dividend at t=5 will be $1.15(1+0.05),
- the dividend at t=6 will be $1.15(1+0.05)^2, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. What is the current price of the stock?
The following is the Dividend Discount Model (DDM) used to price stocks:
### P_0 = \frac{d_1}{r-g} ###Assume that the assumptions of the DDM hold and that the time period is measured in years.
Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
###p_0=\frac{d_1}{r_\text{eff}-g_\text{eff}}###
Which expression is NOT equal to the expected capital return?
A stock pays semi-annual dividends. It just paid a dividend of $10. The growth rate in the dividend is 1% every 6 months, given as an effective 6 month rate. You estimate that the stock's required return is 21% pa, as an effective annual rate.
Using the dividend discount model, what will be the share price?
You own an apartment which you rent out as an investment property.
What is the price of the apartment using discounted cash flow (DCF, same as NPV) valuation?
Assume that:
- You just signed a contract to rent the apartment out to a tenant for the next 12 months at $2,000 per month, payable in advance (at the start of the month, t=0). The tenant is just about to pay you the first $2,000 payment.
- The contract states that monthly rental payments are fixed for 12 months. After the contract ends, you plan to sign another contract but with rental payment increases of 3%. You intend to do this every year.
So rental payments will increase at the start of the 13th month (t=12) to be $2,060 (=2,000(1+0.03)), and then they will be constant for the next 12 months.
Rental payments will increase again at the start of the 25th month (t=24) to be $2,121.80 (=2,000(1+0.03)2), and then they will be constant for the next 12 months until the next year, and so on. - The required return of the apartment is 8.732% pa, given as an effective annual rate.
- Ignore all taxes, maintenance, real estate agent, council and strata fees, periods of vacancy and other costs. Assume that the apartment will last forever and so will the rental payments.
Question 488 income and capital returns, payout policy, payout ratio, DDM
Two companies BigDiv and ZeroDiv are exactly the same except for their dividend payouts.
BigDiv pays large dividends and ZeroDiv doesn't pay any dividends.
Currently the two firms have the same earnings, assets, number of shares, share price, expected total return and risk.
Assume a perfect world with no taxes, no transaction costs, no asymmetric information and that all assets including business projects are fairly priced and therefore zero-NPV.
All things remaining equal, which of the following statements is NOT correct?
Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
- JP Morgan Chase's historical earnings per share (EPS) is $4.37;
- Citi Group's share price is $50.05 and historical EPS is $4.26;
- Wells Fargo's share price is $48.98 and historical EPS is $3.89.
Note: Figures sourced from Google Finance on 24 March 2014.
Estimate the Chinese bank ICBC's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that the renminbi (RMB) is the Chinese currency, also known as the yuan (CNY).
- The 4 major Chinese banks ICBC, China Construction Bank (CCB), Bank of China (BOC) and Agricultural Bank of China (ABC) are comparable companies;
- ICBC 's historical earnings per share (EPS) is RMB 0.74;
- CCB's backward-looking PE ratio is 4.59;
- BOC 's backward-looking PE ratio is 4.78;
- ABC's backward-looking PE ratio is also 4.78;
Note: Figures sourced from Google Finance on 25 March 2014. Share prices are from the Shanghai stock exchange.
Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:
- Apple, Google and Microsoft are comparable companies,
- Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
- Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
- Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.
Source: Google Finance 28 Feb 2014.
Which firms tend to have low forward-looking price-earnings (PE) ratios?
Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.
Which firms tend to have low forward-looking price-earnings (PE) ratios? Only consider firms with positive PE ratios.
Private equity firms are known to buy medium sized private companies operating in the same industry, merge them together into a larger company, and then sell it off in a public float (initial public offering, IPO).
If medium-sized private companies trade at PE ratios of 5 and larger listed companies trade at PE ratios of 15, what return can be achieved from this strategy?
Assume that:
- The medium-sized companies can be bought, merged and sold in an IPO instantaneously.
- There are no costs of finding, valuing, merging and restructuring the medium sized companies. Also, there is no competition to buy the medium-sized companies from other private equity firms.
- The large merged firm's earnings are the sum of the medium firms' earnings.
- The only reason for the difference in medium and large firm's PE ratios is due to the illiquidity of the medium firms' shares.
- Return is defined as: ##r_{0→1} = (p_1-p_0+c_1)/p_0## , where time zero is just before the merger and time one is just after.
A low-quality second-hand car can be bought now for $1,000 and will last for 1 year before it will be scrapped for nothing.
A high-quality second-hand car can be bought now for $4,900 and it will last for 5 years before it will be scrapped for nothing.
What is the equivalent annual cost of each car? Assume a discount rate of 10% pa, given as an effective annual rate.
The answer choices are given as the equivalent annual cost of the low-quality car and then the high quality car.
Question 180 equivalent annual cash flow, inflation, real and nominal returns and cash flows
Details of two different types of light bulbs are given below:
- Low-energy light bulbs cost $3.50, have a life of nine years, and use about $1.60 of electricity a year, paid at the end of each year.
- Conventional light bulbs cost only $0.50, but last only about a year and use about $6.60 of energy a year, paid at the end of each year.
The real discount rate is 5%, given as an effective annual rate. Assume that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the Equivalent Annual Cost (EAC) of the low-energy and conventional light bulbs. The below choices are listed in that order.
Carlos and Edwin are brothers and they both love Holden Commodore cars.
Carlos likes to buy the latest Holden Commodore car for $40,000 every 4 years as soon as the new model is released. As soon as he buys the new car, he sells the old one on the second hand car market for $20,000. Carlos never has to bother with paying for repairs since his cars are brand new.
Edwin also likes Commodores, but prefers to buy 4-year old cars for $20,000 and keep them for 11 years until the end of their life (new ones last for 15 years in total but the 4-year old ones only last for another 11 years). Then he sells the old car for $2,000 and buys another 4-year old second hand car, and so on.
Every time Edwin buys a second hand 4 year old car he immediately has to spend $1,000 on repairs, and then $1,000 every year after that for the next 10 years. So there are 11 payments in total from when the second hand car is bought at t=0 to the last payment at t=10. One year later (t=11) the old car is at the end of its total 15 year life and can be scrapped for $2,000.
Assuming that Carlos and Edwin maintain their love of Commodores and keep up their habits of buying new ones and second hand ones respectively, how much larger is Carlos' equivalent annual cost of car ownership compared with Edwin's?
The real discount rate is 10% pa. All cash flows are real and are expected to remain constant. Inflation is forecast to be 3% pa. All rates are effective annual. Ignore capital gains tax and tax savings from depreciation since cars are tax-exempt for individuals.
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Profitability Index (PI) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 200 |
| 2 | 250 |
What is the Profitability Index (PI) of the project? Assume that the cash flows shown in the table are paid all at once at the given point in time. The required return is 10% pa, given as an effective annual rate.
A project's Profitability Index (PI) is less than 1. Select the most correct statement:
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -90 |
| 1 | 30 |
| 2 | 105 |
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Profitability Index (PI) of the project?
The required return of a project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
What is the Net Present Value (NPV) of the project?
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
What is the Internal Rate of Return (IRR) of the project detailed in the table below?
Assume that the cash flows shown in the table are paid all at once at the given point in time. All answers are given as effective annual rates.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 0 |
| 2 | 121 |
If a project's net present value (NPV) is zero, then its internal rate of return (IRR) will be:
The required return of a building project is 10%, given as an effective annual rate. Assume that the cash flows shown in the table are paid all at once at the given point in time.
The building firm is just about to start the project and the client has signed the contract. Initially the firm will pay $100 to the sub-contractors to carry out the work and then will receive an $11 payment from the client in one year and $121 when the project is finished in 2 years. Ignore credit risk.
But the building company is considering selling the project to a competitor at different points in time and is pondering the minimum price that they should sell it for.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
Which of the below statements is NOT correct? The project is worth:
The required return of a project is 10%, given as an effective annual rate.
What is the payback period of the project in years?
Assume that the cash flows shown in the table are received smoothly over the year. So the $121 at time 2 is actually earned smoothly from t=1 to t=2.
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -100 |
| 1 | 11 |
| 2 | 121 |
A project has the following cash flows:
| Project Cash Flows | |
| Time (yrs) | Cash flow ($) |
| 0 | -400 |
| 1 | 0 |
| 2 | 500 |
What is the payback period of the project in years?
Normally cash flows are assumed to happen at the given time. But here, assume that the cash flows are received smoothly over the year. So the $500 at time 2 is actually earned smoothly from t=1 to t=2.
The below graph shows a project's net present value (NPV) against its annual discount rate.
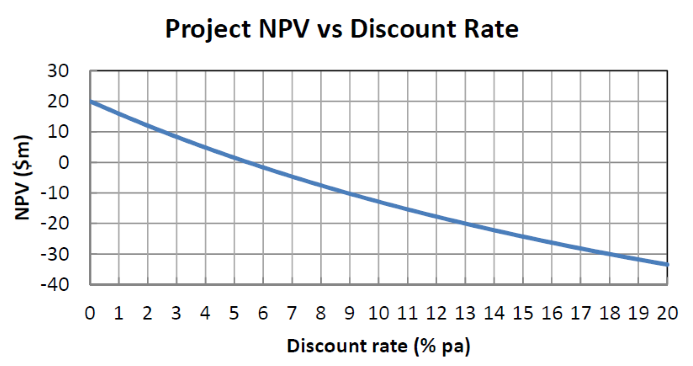
For what discount rate or range of discount rates would you accept and commence the project?
All answer choices are given as approximations from reading off the graph.
The below graph shows a project's net present value (NPV) against its annual discount rate.

Which of the following statements is NOT correct?
You have $100,000 in the bank. The bank pays interest at 10% pa, given as an effective annual rate.
You wish to consume an equal amount now (t=0) and in one year (t=1) and have nothing left in the bank at the end (t=1).
How much can you consume at each time?
An investor owns an empty block of land that has local government approval to be developed into a petrol station, car wash or car park. The council will only allow a single development so the projects are mutually exclusive.
All of the development projects have the same risk and the required return of each is 10% pa. Each project has an immediate cost and once construction is finished in one year the land and development will be sold. The table below shows the estimated costs payable now, expected sale prices in one year and the internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cost now ($) |
Sale price in one year ($) |
IRR (% pa) |
| Petrol station | 9,000,000 | 11,000,000 | 22.22 |
| Car wash | 800,000 | 1,100,000 | 37.50 |
| Car park | 70,000 | 110,000 | 57.14 |
Which project should the investor accept?
Question 579 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to double if the price grows by 10% pa?
An investor owns a whole level of an old office building which is currently worth $1 million. There are three mutually exclusive projects that can be started by the investor. The office building level can be:
- Rented out to a tenant for one year at $0.1m paid immediately, and then sold for $0.99m in one year.
- Refurbished into more modern commercial office rooms at a cost of $1m now, and then sold for $2.4m when the refurbishment is finished in one year.
- Converted into residential apartments at a cost of $2m now, and then sold for $3.4m when the conversion is finished in one year.
All of the development projects have the same risk so the required return of each is 10% pa. The table below shows the estimated cash flows and internal rates of returns (IRR's).
| Mutually Exclusive Projects | |||
| Project | Cash flow now ($) |
Cash flow in one year ($) |
IRR (% pa) |
| Rent then sell as is | -900,000 | 990,000 | 10 |
| Refurbishment into modern offices | -2,000,000 | 2,400,000 | 20 |
| Conversion into residential apartments | -3,000,000 | 3,400,000 | 13.33 |
Which project should the investor accept?
Question 580 price gains and returns over time, time calculation, effective rate
How many years will it take for an asset's price to quadruple (be four times as big, say from $1 to $4) if the price grows by 15% pa?
A home loan company advertises an interest rate of 6% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given to four decimal places.
A credit card offers an interest rate of 18% pa, compounding monthly.
Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###
Calculate the effective annual rates of the following three APR's:
- A credit card offering an interest rate of 18% pa, compounding monthly.
- A bond offering a yield of 6% pa, compounding semi-annually.
- An annual dividend-paying stock offering a return of 10% pa compounding annually.
All answers are given in the same order:
##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##
On his 20th birthday, a man makes a resolution. He will deposit $30 into a bank account at the end of every month starting from now, which is the start of the month. So the first payment will be in one month. He will write in his will that when he dies the money in the account should be given to charity.
The bank account pays interest at 6% pa compounding monthly, which is not expected to change.
If the man lives for another 60 years, how much money will be in the bank account if he dies just after making his last (720th) payment?
You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.
How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.
You want to buy an apartment worth $300,000. You have saved a deposit of $60,000.
The bank has agreed to lend you $240,000 as an interest only mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
Question 239 income and capital returns, inflation, real and nominal returns and cash flows, interest only loan
A bank grants a borrower an interest-only residential mortgage loan with a very large 50% deposit and a nominal interest rate of 6% that is not expected to change. Assume that inflation is expected to be a constant 2% pa over the life of the loan. Ignore credit risk.
From the bank's point of view, what is the long term expected nominal capital return of the loan asset?
Calculate the price of a newly issued ten year bond with a face value of $100, a yield of 8% pa and a fixed coupon rate of 6% pa, paid annually. So there's only one coupon per year, paid in arrears every year.
"Buy low, sell high" is a phrase commonly heard in financial markets. It states that traders should try to buy assets at low prices and sell at high prices.
Traders in the fixed-coupon bond markets often quote promised bond yields rather than prices. Fixed-coupon bond traders should try to:
Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?
The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.
Considering this, which of the following statements is NOT correct?
A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?
A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?
Which one of the following bonds is trading at a discount?
Which one of the following bonds is trading at a premium?
An investor bought two fixed-coupon bonds issued by the same company, a zero-coupon bond and a 7% pa semi-annual coupon bond. Both bonds have a face value of $1,000, mature in 10 years, and had a yield at the time of purchase of 8% pa.
A few years later, yields fell to 6% pa. Which of the following statements is correct? Note that a capital gain is an increase in price.
A 10 year bond has a face value of $100, a yield of 6% pa and a fixed coupon rate of 8% pa, paid semi-annually. What is its price?
Below are some statements about loans and bonds. The first descriptive sentence is correct. But one of the second sentences about the loans' or bonds' prices is not correct. Which statement is NOT correct? Assume that interest rates are positive.
Note that coupons or interest payments are the periodic payments made throughout a bond or loan's life. The face or par value of a bond or loan is the amount paid at the end when the debt matures.
Question 35 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
A European company just issued two bonds, a
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
Question 143 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 6-month zero coupon bond at a yield of 6% pa, and
- A 12 month zero coupon bond at a yield of 7% pa.
What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 96 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds paying semi-annual coupons:
- 1 year zero coupon bond at a yield of 8% pa, and a
- 2 year zero coupon bond at a yield of 10% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
You're trying to save enough money to buy your first car which costs $2,500. You can save $100 at the end of each month starting from now. You currently have no money at all. You just opened a bank account with an interest rate of 6% pa payable monthly.
How many months will it take to save enough money to buy the car? Assume that the price of the car will stay the same over time.
Your main expense is fuel for your car which costs $100 per month. You just refueled, so you won't need any more fuel for another month (first payment at t=1 month).
You have $2,500 in a bank account which pays interest at a rate of 6% pa, payable monthly. Interest rates are not expected to change.
Assuming that you have no income, in how many months time will you not have enough money to fully refuel your car?
A young lady is trying to decide if she should attend university or not.
The young lady's parents say that she must attend university because otherwise all of her hard work studying and attending school during her childhood was a waste.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The hard work studying at school in her childhood should be classified as:
A young lady is trying to decide if she should attend university. Her friends say that she should go to university because she is more likely to meet a clever young man than if she begins full time work straight away.
What's the correct way to classify this item from a capital budgeting perspective when trying to find the Net Present Value of going to university rather than working?
The opportunity to meet a desirable future spouse should be classified as:
A man is thinking about taking a day off from his casual painting job to relax.
He just woke up early in the morning and he's about to call his boss to say that he won't be coming in to work.
But he's thinking about the hours that he could work today (in the future) which are:
Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?
###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###
A firm has forecast its Cash Flow From Assets (CFFA) for this year and management is worried that it is too low. Which one of the following actions will lead to a higher CFFA for this year (t=0 to 1)? Only consider cash flows this year. Do not consider cash flows after one year, or the change in the NPV of the firm. Consider each action in isolation.
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###Find Ching-A-Lings Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Ching-A-Lings Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 20 | |
| Depreciation | 20 | |
| Rent expense | 11 | |
| Interest expense | 19 | |
| Taxable Income | 30 | |
| Taxes at 30% | 9 | |
| Net income | 21 | |
| Ching-A-Lings Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Inventory | 49 | 38 |
| Trade debtors | 14 | 2 |
| Rent paid in advance | 5 | 5 |
| PPE | 400 | 400 |
| Total assets | 468 | 445 |
| Trade creditors | 4 | 10 |
| Bond liabilities | 200 | 190 |
| Contributed equity | 145 | 145 |
| Retained profits | 119 | 100 |
| Total L and OE | 468 | 445 |
Note: All figures are given in millions of dollars ($m).
The cash flow from assets was:
Over the next year, the management of an unlevered company plans to:
- Make $5m in sales, $1.9m in net income and $2m in equity free cash flow (EFCF).
- Pay dividends of $1m.
- Complete a $1.3m share buy-back.
Assume that:
- All amounts are received and paid at the end of the year so you can ignore the time value of money.
- The firm has sufficient retained profits to legally pay the dividend and complete the buy back.
- The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.
How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?
Read the following financial statements and calculate the firm's free cash flow over the 2014 financial year.
| UBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2014 | ||
| $m | ||
| Sales | 293 | |
| COGS | 200 | |
| Rent expense | 15 | |
| Gas expense | 8 | |
| Depreciation | 10 | |
| EBIT | 60 | |
| Interest expense | 0 | |
| Taxable income | 60 | |
| Taxes | 18 | |
| Net income | 42 | |
| UBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2014 | 2013 |
| $m | $m | |
| Assets | ||
| Cash | 30 | 29 |
| Accounts receivable | 5 | 7 |
| Pre-paid rent expense | 1 | 0 |
| Inventory | 50 | 46 |
| PPE | 290 | 300 |
| Total assets | 376 | 382 |
| Liabilities | ||
| Trade payables | 20 | 18 |
| Accrued gas expense | 3 | 2 |
| Non-current liabilities | 0 | 0 |
| Contributed equity | 212 | 212 |
| Retained profits | 136 | 150 |
| Asset revaluation reserve | 5 | 0 |
| Total L and OE | 376 | 382 |
Note: all figures are given in millions of dollars ($m).
The firm's free cash flow over the 2014 financial year was:
Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Trademark Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 100 | |
| COGS | 25 | |
| Operating expense | 5 | |
| Depreciation | 20 | |
| Interest expense | 20 | |
| Income before tax | 30 | |
| Tax at 30% | 9 | |
| Net income | 21 | |
| Trademark Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 80 |
| PPE | ||
| Cost | 150 | 140 |
| Accumul. depr. | 60 | 40 |
| Carrying amount | 90 | 100 |
| Total assets | 210 | 180 |
| Liabilities | ||
| Current liabilities | 75 | 65 |
| Non-current liabilities | 75 | 55 |
| Owners' equity | ||
| Retained earnings | 10 | 10 |
| Contributed equity | 50 | 50 |
| Total L and OE | 210 | 180 |
Note: all figures are given in millions of dollars ($m).
Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| UniBar Corp | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 80 | |
| COGS | 40 | |
| Operating expense | 15 | |
| Depreciation | 10 | |
| Interest expense | 5 | |
| Income before tax | 10 | |
| Tax at 30% | 3 | |
| Net income | 7 | |
| UniBar Corp | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 120 | 90 |
| PPE | ||
| Cost | 360 | 320 |
| Accumul. depr. | 40 | 30 |
| Carrying amount | 320 | 290 |
| Total assets | 440 | 380 |
| Liabilities | ||
| Current liabilities | 110 | 60 |
| Non-current liabilities | 190 | 180 |
| Owners' equity | ||
| Retained earnings | 95 | 95 |
| Contributed equity | 45 | 45 |
| Total L and OE | 440 | 380 |
Note: all figures are given in millions of dollars ($m).
Find the cash flow from assets (CFFA) of the following project.
| One Year Mining Project Data | ||
| Project life | 1 year | |
| Initial investment in building mine and equipment | $9m | |
| Depreciation of mine and equipment over the year | $8m | |
| Kilograms of gold mined at end of year | 1,000 | |
| Sale price per kilogram | $0.05m | |
| Variable cost per kilogram | $0.03m | |
| Before-tax cost of closing mine at end of year | $4m | |
| Tax rate | 30% | |
Note 1: Due to the project, the firm also anticipates finding some rare diamonds which will give before-tax revenues of $1m at the end of the year.
Note 2: The land that will be mined actually has thermal springs and a family of koalas that could be sold to an eco-tourist resort for an after-tax amount of $3m right now. However, if the mine goes ahead then this natural beauty will be destroyed.
Note 3: The mining equipment will have a book value of $1m at the end of the year for tax purposes. However, the equipment is expected to fetch $2.5m when it is sold.
Find the project's CFFA at time zero and one. Answers are given in millions of dollars ($m), with the first cash flow at time zero, and the second at time one.
Find the cash flow from assets (CFFA) of the following project.
| Project Data | ||
| Project life | 2 years | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year for tax purposes | $1m | |
| Unit sales per year | 4m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $3 | |
| Fixed costs per year, paid at the end of each year | $1.5m | |
| Tax rate | 30% | |
Note 1: The equipment will have a book value of $4m at the end of the project for tax purposes. However, the equipment is expected to fetch $0.9 million when it is sold at t=2.
Note 2: Due to the project, the firm will have to purchase $0.8m of inventory initially, which it will sell at t=1. The firm will buy another $0.8m at t=1 and sell it all again at t=2 with zero inventory left. The project will have no effect on the firm's current liabilities.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.
In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.
If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.
Remember:
### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###
where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.
Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.
In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.
If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?
Assume that:
- No income (rent) was received from the house during the short time over which house prices fell.
- Your friend will not declare bankruptcy, he will always pay off his debts.
One year ago you bought $100,000 of shares partly funded using a margin loan. The margin loan size was $70,000 and the other $30,000 was your own wealth or 'equity' in the share assets.
The interest rate on the margin loan was 7.84% pa.
Over the year, the shares produced a dividend yield of 4% pa and a capital gain of 5% pa.
What was the total return on your wealth? Ignore taxes, assume that all cash flows (interest payments and dividends) were paid and received at the end of the year, and all rates above are effective annual rates.
Hint: Remember that wealth in this context is your equity (E) in the house asset (V = D+E) which is funded by the loan (D) and your deposit or equity (E).
Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?
Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.
Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?
Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?
Remember:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.
Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.
Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.
The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.
Assume the following:
- Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
- Motorola had a 20% after-tax WACC before it merged with Google.
- Google and Motorola have the same level of gearing.
- Both companies operate in a classical tax system.
You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.
The mobile phone manufacturing project's:
A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use earnings before interest and tax (EBIT).
###\begin{aligned} FFCF &= (EBIT)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ \end{aligned} \\###
One method for calculating a firm's free cash flow (FFCF, or CFFA) is to ignore interest expense. That is, pretend that interest expense ##(IntExp)## is zero:
###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp \\ &= (Rev - COGS - Depr - FC - 0)(1-t_c) + Depr - CapEx -\Delta NWC - 0\\ \end{aligned}###
One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use net operating profit after tax (NOPAT).
###\begin{aligned} FFCF &= NOPAT + Depr - CapEx -\Delta NWC \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC \\ \end{aligned} \\###
Question 370 capital budgeting, NPV, interest tax shield, WACC, CFFA
| Project Data | ||
| Project life | 2 yrs | |
| Initial investment in equipment | $600k | |
| Depreciation of equipment per year | $250k | |
| Expected sale price of equipment at end of project | $200k | |
| Revenue per job | $12k | |
| Variable cost per job | $4k | |
| Quantity of jobs per year | 120 | |
| Fixed costs per year, paid at the end of each year | $100k | |
| Interest expense in first year (at t=1) | $16.091k | |
| Interest expense in second year (at t=2) | $9.711k | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Levered cost of equity | 12.5% | |
| Market portfolio return | 10% | |
| Beta of assets | 1.24 | |
| Beta of levered equity | 1.5 | |
| Firm's and project's debt-to-equity ratio | 25% | |
Notes
- The project will require an immediate purchase of $50k of inventory, which will all be sold at cost when the project ends. Current liabilities are negligible so they can be ignored.
Assumptions
- The debt-to-equity ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio. Note that interest expense is different in each year.
- Thousands are represented by 'k' (kilo).
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are nominal. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Question 69 interest tax shield, capital structure, leverage, WACC
Which statement about risk, required return and capital structure is the most correct?
A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?
A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.
In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of equity to raise money for new projects of similar systematic risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Question 99 capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.
Assume that:
- The firm and individual investors can borrow at the same rate and have the same tax rates.
- The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
- There are no market frictions relating to debt such as asymmetric information or transaction costs.
- Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.
According to Miller and Modigliani's theory, which statement is correct?
A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?
Question 121 capital structure, leverage, financial distress, interest tax shield
Fill in the missing words in the following sentence:
All things remaining equal, as a firm's amount of debt funding falls, benefits of interest tax shields __________ and the costs of financial distress __________.
Question 337 capital structure, interest tax shield, leverage, real and nominal returns and cash flows, multi stage growth model
A fast-growing firm is suitable for valuation using a multi-stage growth model.
It's nominal unlevered cash flow from assets (##CFFA_U##) at the end of this year (t=1) is expected to be $1 million. After that it is expected to grow at a rate of:
- 12% pa for the next two years (from t=1 to 3),
- 5% over the fourth year (from t=3 to 4), and
- -1% forever after that (from t=4 onwards). Note that this is a negative one percent growth rate.
Assume that:
- The nominal WACC after tax is 9.5% pa and is not expected to change.
- The nominal WACC before tax is 10% pa and is not expected to change.
- The firm has a target debt-to-equity ratio that it plans to maintain.
- The inflation rate is 3% pa.
- All rates are given as nominal effective annual rates.
What is the levered value of this fast growing firm's assets?
Question 490 expected and historical returns, accounting ratio
Which of the following is NOT a synonym of 'required return'?
Which of the following equations is NOT equal to the total return of an asset?
Let ##p_0## be the current price, ##p_1## the expected price in one year and ##c_1## the expected income in one year.
A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).
What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:
##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.
In the 'Austin Powers' series of movies, the character Dr. Evil threatens to destroy the world unless the United Nations pays him a ransom (video 1, video 2). Dr. Evil makes the threat on two separate occasions:
- In 1969 he demands a ransom of $1 million (=10^6), and again;
- In 1997 he demands a ransom of $100 billion (=10^11).
If Dr. Evil's demands are equivalent in real terms, in other words $1 million will buy the same basket of goods in 1969 as $100 billion would in 1997, what was the implied inflation rate over the 28 years from 1969 to 1997?
The answer choices below are given as effective annual rates:
Question 155 inflation, real and nominal returns and cash flows, Loan, effective rate conversion
You are a banker about to grant a 2 year loan to a customer. The loan's principal and interest will be repaid in a single payment at maturity, sometimes called a zero-coupon loan, discount loan or bullet loan.
You require a real return of 6% pa over the two years, given as an effective annual rate. Inflation is expected to be 2% this year and 4% next year, both given as effective annual rates.
You judge that the customer can afford to pay back $1,000,000 in 2 years, given as a nominal cash flow. How much should you lend to her right now?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation ##(\rho_{A,B})## | Dollars invested |
||
| A | 0.1 | 0.4 | 0.5 | 60 | ||
| B | 0.2 | 0.6 | 140 | |||
What is the standard deviation (not variance) of returns of the above portfolio?
Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.
If the variance of stock A's returns increases but the:
- Prices and expected returns of each stock stays the same,
- Variance of stock B's returns stays the same,
- Correlation of returns between the stocks stays the same.
Which of the following statements is NOT correct?
All things remaining equal, the higher the correlation of returns between two stocks:
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 6% pa.
- Stock A has an expected return of 5% pa.
- Stock B has an expected return of 10% pa.
What portfolio weights should the investor have in stocks A and B respectively?
Question 556 portfolio risk, portfolio return, standard deviation
An investor wants to make a portfolio of two stocks A and B with a target expected portfolio return of 12% pa.
- Stock A has an expected return of 10% pa and a standard deviation of 20% pa.
- Stock B has an expected return of 15% pa and a standard deviation of 30% pa.
The correlation coefficient between stock A and B's expected returns is 70%.
What will be the annual standard deviation of the portfolio with this 12% pa target return?
What is the correlation of a variable X with itself?
The corr(X, X) or ##\rho_{X,X}## equals:
Let the standard deviation of returns for a share per month be ##\sigma_\text{monthly}##.
What is the formula for the standard deviation of the share's returns per year ##(\sigma_\text{yearly})##?
Assume that returns are independently and identically distributed (iid) so they have zero auto correlation, meaning that if the return was higher than average today, it does not indicate that the return tomorrow will be higher or lower than average.
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 3 years from now (first payment at t=3).
- 1 payment of $600 in 5 years and 6 months (t=5.5) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
The following cash flows are expected:
- 10 yearly payments of $80, with the first payment in 6.5 years from now (first payment at t=6.5).
- A single payment of $500 in 4 years and 3 months (t=4.25) from now.
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
You are promised 20 payments of $100, where the first payment is immediate (t=0) and the last is at the end of the 19th year (t=19). The effective annual discount rate is ##r##.
Which of the following equations does NOT give the correct present value of these 20 payments?
Telsa Motors advertises that its Model S electric car saves $570 per month in fuel costs. Assume that Tesla cars last for 10 years, fuel and electricity costs remain the same, and savings are made at the end of each month with the first saving of $570 in one month from now.
The effective annual interest rate is 15.8%, and the effective monthly interest rate is 1.23%. What is the present value of the savings?
The present value of an annuity of 3 annual payments of $5,000 in arrears (at the end of each year) is $12,434.26 when interest rates are 10% pa compounding annually.
If the same amount of $12,434.26 is put in the bank at the same interest rate of 10% pa compounded annually and the same cash flow of $5,000 is withdrawn at the end of every year, how much money will be in the bank in 3 years, just after that third $5,000 payment is withdrawn?
Your poor friend asks to borrow some money from you. He would like $1,000 now (t=0) and every year for the next 5 years, so there will be 6 payments of $1,000 from t=0 to t=5 inclusive. In return he will pay you $10,000 in seven years from now (t=7).
What is the net present value (NPV) of lending to your friend?
Assume that your friend will definitely pay you back so the loan is risk-free, and that the yield on risk-free government debt is 10% pa, given as an effective annual rate.
The phone company Optus have 2 mobile service plans on offer which both have the same amount of phone call, text message and internet data credit. Both plans have a contract length of 24 months and the monthly cost is payable in advance. The only difference between the two plans is that one is a:
- 'Bring Your Own' (BYO) mobile service plan, costing $80 per month. There is no phone included in this plan. The other plan is a:
- 'Bundled' mobile service plan that comes with the latest smart phone, costing $100 per month. This plan includes the latest smart phone.
Neither plan has any additional payments at the start or end. Assume that the discount rate is 1% per month given as an effective monthly rate.
The only difference between the plans is the phone, so what is the implied cost of the phone as a present value? Given that the latest smart phone actually costs $600 to purchase outright from another retailer, should you commit to the BYO plan or the bundled plan?
A European bond paying annual coupons of 6% offers a yield of 10% pa.
Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.
All answers are given in the same order:
### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###
Question 49 inflation, real and nominal returns and cash flows, APR, effective rate
In Australia, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 2.83% pa.
The inflation rate is currently 2.2% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
Question 64 inflation, real and nominal returns and cash flows, APR, effective rate
In Germany, nominal yields on semi-annual coupon paying Government Bonds with 2 years until maturity are currently 0.04% pa.
The inflation rate is currently 1.4% pa, given as an APR compounding per quarter. The inflation rate is not expected to change over the next 2 years.
What is the real yield on these bonds, given as an APR compounding every 6 months?
You want to buy an apartment worth $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising mortgage loan with a term of 25 years. The interest rate is 6% pa and is not expected to change.
What will be your monthly payments?
Your credit card shows a $600 debt liability. The interest rate is 24% pa, payable monthly. You can't pay any of the debt off, except in 6 months when it's your birthday and you'll receive $50 which you'll use to pay off the credit card. If that is your only repayment, how much will the credit card debt liability be one year from now?
A three year corporate bond yields 12% pa with a coupon rate of 10% pa, paid semi-annually.
Find the effective six month yield, effective annual yield and the effective daily yield. Assume that each month has 30 days and that there are 360 days in a year.
All answers are given in the same order:
##r_\text{eff semi-annual}##, ##r_\text{eff yearly}##, ##r_\text{eff daily}##.
You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?
You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.
Harvey Norman the large retailer often runs sales advertising 2 years interest free when you purchase its products. This offer can be seen as a free personal loan from Harvey Norman to its customers.
Assume that banks charge an interest rate on personal loans of 12% pa given as an APR compounding per month. This is the interest rate that Harvey Norman deserves on the 2 year loan it extends to its customers. Therefore Harvey Norman must implicitly include the cost of this loan in the advertised sale price of its goods.
If you were a customer buying from Harvey Norman, and you were paying immediately, not in 2 years, what is the minimum percentage discount to the advertised sale price that you would insist on? (Hint: if it makes it easier, assume that you’re buying a product with an advertised price of $100).
You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.
To your surprise, you can actually afford to pay $2,000 per month and your mortgage allows early repayments without fees. If you maintain these higher monthly payments, how long will it take to pay off your mortgage?
You just started work at your new job which pays $48,000 per year.
The human resources department have given you the option of being paid at the end of every week or every month.
Assume that there are 4 weeks per month, 12 months per year and 48 weeks per year.
Bank interest rates are 12% pa given as an APR compounding per month.
What is the dollar gain over one year, as a net present value, of being paid every week rather than every month?
A 2 year corporate bond yields 3% pa with a coupon rate of 5% pa, paid semi-annually.
Find the effective monthly rate, effective six month rate, and effective annual rate.
##r_\text{eff monthly}##, ##r_\text{eff 6 month}##, ##r_\text{eff annual}##.
You're trying to save enough money for a deposit to buy a house. You want to buy a house worth $400,000 and the bank requires a 20% deposit ($80,000) before it will give you a loan for the other $320,000 that you need.
You currently have no savings, but you just started working and can save $2,000 per month, with the first payment in one month from now. Bank interest rates on savings accounts are 4.8% pa with interest paid monthly and interest rates are not expected to change.
How long will it take to save the $80,000 deposit? Round your answer up to the nearest month.
Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Which one of the below statements about effective rates and annualised percentage rates (APR's) is NOT correct?
Question 524 risk, expected and historical returns, bankruptcy or insolvency, capital structure, corporate financial decision theory, limited liability
Which of the following statements is NOT correct?
Question 461 book and market values, ROE, ROA, market efficiency
One year ago a pharmaceutical firm floated by selling its 1 million shares for $100 each. Its book and market values of equity were both $100m. Its debt totalled $50m. The required return on the firm's assets was 15%, equity 20% and debt 5% pa.
In the year since then, the firm:
- Earned net income of $29m.
- Paid dividends totaling $10m.
- Discovered a valuable new drug that will lead to a massive 1,000 times increase in the firm's net income in 10 years after the research is commercialised. News of the discovery was publicly announced. The firm's systematic risk remains unchanged.
Which of the following statements is NOT correct? All statements are about current figures, not figures one year ago.
Hint: Book return on assets (ROA) and book return on equity (ROE) are ratios that accountants like to use to measure a business's past performance.
###\text{ROA}= \dfrac{\text{Net income}}{\text{Book value of assets}}###
###\text{ROE}= \dfrac{\text{Net income}}{\text{Book value of equity}}###
The required return on assets ##r_V## is a return that financiers like to use to estimate a business's future required performance which compensates them for the firm's assets' risks. If the business were to achieve realised historical returns equal to its required returns, then investment into the business's assets would have been a zero-NPV decision, which is neither good nor bad but fair.
###r_\text{V, 0 to 1}= \dfrac{\text{Cash flow from assets}_\text{1}}{\text{Market value of assets}_\text{0}} = \dfrac{CFFA_\text{1}}{V_\text{0}}###
Similarly for equity and debt.
Question 729 book and market values, balance sheet, no explanation
If a firm makes a profit and pays no dividends, which of the firm’s accounts will increase?
Question 768 accounting terminology, book and market values, no explanation
Accountants and finance professionals have lots of names for the same things which can be quite confusing.
Which of the following groups of items are NOT synonyms?
Which one of the following businesses is likely to be a public company in Australia, judging by its name?
Question 446 working capital decision, corporate financial decision theory
The working capital decision primarily affects which part of a business?
Question 447 payout policy, corporate financial decision theory
Payout policy is most closely related to which part of a business?
Which of the following decisions relates to the current assets and current liabilities of the firm?
Question 767 idiom, corporate financial decision theory, no explanation
The sayings "Don't cry over spilt milk", "Don't regret the things that you can't change" and "What's done is done" are most closely related to which financial concept?
In his survey paper from 1956, John Lintner stated: “A prudent foresighted management will always do its best to plan ahead in all aspects of financial policy to avoid getting into such uncomfortable situations where dividends have to be cut substantially below those which the company's previous practice would lead stockholders to expect on the basis of current earnings.”
This is a statement about which decision made by financial managers?
Which of the following statements is NOT equivalent to the yield on debt?
Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.
You bought a house, primarily funded using a home loan from a bank. Which of the following statements is NOT correct?
Question 771 debt terminology, interest expense, interest tax shield, credit risk, no explanation
You deposit money into a bank account. Which of the following statements about this deposit is NOT correct?
Question 987 interest tax shield, capital structure, debt terminology
What creates interest tax shields for a company?
Question 22 NPV, perpetuity with growth, effective rate, effective rate conversion
What is the NPV of the following series of cash flows when the discount rate is 10% given as an effective annual rate?
The first payment of $90 is in 3 years, followed by payments every 6 months in perpetuity after that which shrink by 3% every 6 months. That is, the growth rate every 6 months is actually negative 3%, given as an effective 6 month rate. So the payment at ## t=3.5 ## years will be ## 90(1-0.03)^1=87.3 ##, and so on.
Question 249 equivalent annual cash flow, effective rate conversion
Details of two different types of desserts or edible treats are given below:
- High-sugar treats like candy, chocolate and ice cream make a person very happy. High sugar treats are cheap at only $2 per day.
- Low-sugar treats like nuts, cheese and fruit make a person equally happy if these foods are of high quality. Low sugar treats are more expensive at $4 per day.
The advantage of low-sugar treats is that a person only needs to pay the dentist $2,000 for fillings and root canal therapy once every 15 years. Whereas with high-sugar treats, that treatment needs to be done every 5 years.
The real discount rate is 10%, given as an effective annual rate. Assume that there are 365 days in every year and that all cash flows are real. The inflation rate is 3% given as an effective annual rate.
Find the equivalent annual cash flow (EAC) of the high-sugar treats and low-sugar treats, including dental costs. The below choices are listed in that order.
Ignore the pain of dental therapy, personal preferences and other factors.
An effective semi-annual return of 5% ##(r_\text{eff 6mth})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
An effective monthly return of 1% ##(r_\text{eff monthly})## is equivalent to an effective annual return ##(r_\text{eff annual})## of:
Question 662 APR, effective rate, effective rate conversion, no explanation
Which of the following interest rate labels does NOT make sense?
Question 659 APR, effective rate, effective rate conversion, no explanation
A home loan company advertises an interest rate of 9% pa, payable monthly. Which of the following statements about the interest rate is NOT correct? All rates are given with an accuracy of 4 decimal places.
Question 658 CFFA, income statement, balance sheet, no explanation
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the income statement needed? Note that the income statement is sometimes also called the profit and loss, P&L, or statement of financial performance.
Question 737 financial statement, balance sheet, income statement
Where can a publicly listed firm's book value of equity be found? It can be sourced from the company's:
Question 738 financial statement, balance sheet, income statement
Where can a private firm's market value of equity be found? It can be sourced from the company's:
For a price of $100, Vera will sell you a 2 year bond paying semi-annual coupons of 10% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 8% pa.
For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.
For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $100, Andrea will sell you a 2 year bond paying annual coupons of 10% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.
For a price of $95, Nicole will sell you a 10 year bond paying semi-annual coupons of 8% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 8% pa.
A three year bond has a face value of $100, a yield of 10% and a fixed coupon rate of 5%, paid semi-annually. What is its price?
A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.
The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.
Question 108 bond pricing, zero coupon bond, term structure of interest rates, forward interest rate
An Australian company just issued two bonds:
- A 1 year zero coupon bond at a yield of 10% pa, and
- A 2 year zero coupon bond at a yield of 8% pa.
What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.
Question 572 bond pricing, zero coupon bond, term structure of interest rates, expectations hypothesis, forward interest rate, yield curve
In the below term structure of interest rates equation, all rates are effective annual yields and the numbers in subscript represent the years that the yields are measured over:
###(1+r_{0-3})^3 = (1+r_{0-1})(1+r_{1-2})(1+r_{2-3}) ###
Which of the following statements is NOT correct?
Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.
Which bond would have the higher current price?
A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?
A two year Government bond has a face value of $100, a yield of 2.5% pa and a fixed coupon rate of 0.5% pa, paid semi-annually. What is its price?
Question 56 income and capital returns, bond pricing, premium par and discount bonds
Which of the following statements about risk free government bonds is NOT correct?
Hint: Total return can be broken into income and capital returns as follows:
###\begin{aligned} r_\text{total} &= \frac{c_1}{p_0} + \frac{p_1-p_0}{p_0} \\ &= r_\text{income} + r_\text{capital} \end{aligned} ###
The capital return is the growth rate of the price.
The income return is the periodic cash flow. For a bond this is the coupon payment.
Bonds A and B are issued by the same Australian company. Both bonds yield 7% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond A pays coupons of 10% pa and bond B pays coupons of 5% pa. Which of the following statements is true about the bonds' prices?
Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100), maturity (3 years) and yield (10%) as each other.
Which of the following statements is true?
Question 207 income and capital returns, bond pricing, coupon rate, no explanation
For a bond that pays fixed semi-annual coupons, how is the annual coupon rate defined, and how is the bond's annual income yield from time 0 to 1 defined mathematically?
Let: ##P_0## be the bond price now,
##F_T## be the bond's face value,
##T## be the bond's maturity in years,
##r_\text{total}## be the bond's total yield,
##r_\text{income}## be the bond's income yield,
##r_\text{capital}## be the bond's capital yield, and
##C_t## be the bond's coupon at time t in years. So ##C_{0.5}## is the coupon in 6 months, ##C_1## is the coupon in 1 year, and so on.
Question 536 idiom, bond pricing, capital structure, leverage
The expression 'my word is my bond' is often used in everyday language to make a serious promise.
Why do you think this expression uses the metaphor of a bond rather than a share?
Question 538 bond pricing, income and capital returns, no explanation
Risk-free government bonds that have coupon rates greater than their yields:
A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 3 years and have a face value of $100 each. Bond yields are 5% pa, given as an APR compounding every 6 months, and the yield curve is flat.
How many bonds should the firm issue?
An investor bought a 5 year government bond with a 2% pa coupon rate at par. Coupons are paid semi-annually. The face value is $100.
Calculate the bond's new price 8 months later after yields have increased to 3% pa. Note that both yields are given as APR's compounding semi-annually. Assume that the yield curve was flat before the change in yields, and remained flat afterwards as well.
A four year bond has a face value of $100, a yield of 6% and a fixed coupon rate of 12%, paid semi-annually. What is its price?
Which one of the following bonds is trading at par?
Question 770 expected and historical returns, income and capital returns, coupon rate, bond pricing
Which of the following statements is NOT correct? Assume that all events are a surprise and that all other things remain equal. So for example, don't assume that just because a company's dividends and profit rise that its required return will also rise, assume the required return stays the same.
Estimate the French bank Societe Generale's share price using a backward-looking price earnings (PE) multiples approach with the following assumptions and figures only. Note that EUR is the euro, the European monetary union's currency.
- The 4 major European banks Credit Agricole (ACA), Deutsche Bank AG (DBK), UniCredit (UCG) and Banco Santander (SAN) are comparable companies to Societe Generale (GLE);
- Societe Generale's (GLE's) historical earnings per share (EPS) is EUR 2.92;
- ACA's backward-looking PE ratio is 16.29 and historical EPS is EUR 0.84;
- DBK's backward-looking PE ratio is 25.01 and historical EPS is EUR 1.26;
- SAN's backward-looking PE ratio is 14.71 and historical EPS is EUR 0.47;
- UCG's backward-looking PE ratio is 15.78 and historical EPS is EUR 0.40;
Note: Figures sourced from Google Finance on 27 March 2015.
Question 990 Multiples valuation, EV to EBITDA ratio, enterprise value
A firm has:
2 million shares;
$200 million EBITDA expected over the next year;
$100 million in cash (not included in EV);
1/3 market debt-to-assets ratio is (market assets = EV + cash);
4% pa expected dividend yield over the next year, paid annually with the next dividend expected in one year;
2% pa expected dividend growth rate;
40% expected payout ratio over the next year;10 times EV/EBITDA ratio.
30% corporate tax rate.
The stock can be valued using the EV/EBITDA multiple, dividend discount model, Gordon growth model or PE multiple. Which of the below statements is NOT correct based on an EV/EBITDA multiple valuation?
A European company just issued two bonds, a
- 3 year zero coupon bond at a yield of 6% pa, and a
- 4 year zero coupon bond at a yield of 6.5% pa.
What is the company's forward rate over the fourth year (from t=3 to t=4)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.
A young lady is trying to decide if she should attend university or begin working straight away in her home town.
The young lady's grandma says that she should not go to university because she is less likely to marry the local village boy whom she likes because she will spend less time with him if she attends university.
What's the correct way to classify this item from a capital budgeting perspective when trying to decide whether to attend university?
The cost of not marrying the local village boy should be classified as:
The 'time value of money' is most closely related to which of the following concepts?
Question 522 income and capital returns, real and nominal returns and cash flows, inflation, real estate
A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 2.5% pa. Inflation is expected to be 2.5% pa.
All of the above are effective nominal rates and investors believe that they will stay the same in perpetuity.
What are the property's expected real total, capital and income returns?
The answer choices below are given in the same order.
Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| Piano Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 310 | |
| COGS | 185 | |
| Operating expense | 20 | |
| Depreciation | 15 | |
| Interest expense | 10 | |
| Income before tax | 80 | |
| Tax at 30% | 24 | |
| Net income | 56 | |
| Piano Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 240 | 230 |
| PPE | ||
| Cost | 420 | 400 |
| Accumul. depr. | 50 | 35 |
| Carrying amount | 370 | 365 |
| Total assets | 610 | 595 |
| Liabilities | ||
| Current liabilities | 180 | 190 |
| Non-current liabilities | 290 | 265 |
| Owners' equity | ||
| Retained earnings | 90 | 90 |
| Contributed equity | 50 | 50 |
| Total L and OE | 610 | 595 |
Note: all figures are given in millions of dollars ($m).
Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.
| World Bar | ||
| Income Statement for | ||
| year ending 30th June 2013 | ||
| $m | ||
| Sales | 300 | |
| COGS | 150 | |
| Operating expense | 50 | |
| Depreciation | 40 | |
| Interest expense | 10 | |
| Taxable income | 50 | |
| Tax at 30% | 15 | |
| Net income | 35 | |
| World Bar | ||
| Balance Sheet | ||
| as at 30th June | 2013 | 2012 |
| $m | $m | |
| Assets | ||
| Current assets | 200 | 230 |
| PPE | ||
| Cost | 400 | 400 |
| Accumul. depr. | 75 | 35 |
| Carrying amount | 325 | 365 |
| Total assets | 525 | 595 |
| Liabilities | ||
| Current liabilities | 150 | 205 |
| Non-current liabilities | 235 | 250 |
| Owners' equity | ||
| Retained earnings | 100 | 100 |
| Contributed equity | 40 | 40 |
| Total L and OE | 525 | 595 |
Note: all figures above and below are given in millions of dollars ($m).
Find the cash flow from assets (CFFA) of the following project.
| Project Data | |
| Project life | 2 years |
| Initial investment in equipment | $8m |
| Depreciation of equipment per year for tax purposes | $3m |
| Unit sales per year | 10m |
| Sale price per unit | $9 |
| Variable cost per unit | $4 |
| Fixed costs per year, paid at the end of each year | $2m |
| Tax rate | 30% |
Note 1: Due to the project, the firm will have to purchase $40m of inventory initially (at t=0). Half of this inventory will be sold at t=1 and the other half at t=2.
Note 2: The equipment will have a book value of $2m at the end of the project for tax purposes. However, the equipment is expected to fetch $1m when it is sold. Assume that the full capital loss is tax-deductible and taxed at the full corporate tax rate.
Note 3: The project will be fully funded by equity which investors will expect to pay dividends totaling $10m at the end of each year.
Find the project's CFFA at time zero, one and two. Answers are given in millions of dollars ($m).
To value a business's assets, the free cash flow of the firm (FCFF, also called CFFA) needs to be calculated. This requires figures from the firm's income statement and balance sheet. For what figures is the balance sheet needed? Note that the balance sheet is sometimes also called the statement of financial position.
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_{0} = \frac{c_1}{r_{\text{eff}} - g_{\text{eff}}} ###
What is the discount rate '## r_\text{eff} ##' in this equation?
Here's the Dividend Discount Model, used to price stocks:
### p_0=\frac{d_1}{r-g} ###
All rates are effective annual rates and the cash flows (##d_1##) are received every year. Note that the r and g terms in the above DDM could also be labelled: ###r = r_{\text{total, 0}\rightarrow\text{1yr, eff 1yr}}### ###g = r_{\text{capital, 0}\rightarrow\text{1yr, eff 1yr}}### Which of the following statements is NOT correct?
A company's shares just paid their annual dividend of $2 each.
The stock price is now $40 (just after the dividend payment). The annual dividend is expected to grow by 3% every year forever. The assumptions of the dividend discount model are valid for this company.
What do you expect the effective annual dividend yield to be in 3 years (dividend yield from t=3 to t=4)?
The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.
### p_0= \frac{c_1}{r-g} ###
Which expression is equal to the expected dividend return?
Three years ago Frederika bought a house for $400,000.
Now it's worth $600,000, based on recent similar sales in the area.
Frederika's residential property has an expected total return of 7% pa.
She rents her house out for $2,500 per month, paid in advance. Every 12 months she plans to increase the rental payments.
The present value of 12 months of rental payments is $29,089.48.
The future value of 12 months of rental payments one year ahead is $31,125.74.
What is the expected annual capital yield of the property?
Question 405 DDM, income and capital returns, no explanation
The perpetuity with growth formula is:
###P_0= \dfrac{C_1}{r-g}###
Which of the following is NOT equal to the total required return (r)?
The perpetuity with growth equation is:
###P_0=\dfrac{C_1}{r-g}###
Which of the following is NOT equal to the expected capital return as an effective annual rate?
Question 455 income and capital returns, payout policy, DDM, market efficiency
A fairly priced unlevered firm plans to pay a dividend of $1 next year (t=1) which is expected to grow by 3% pa every year after that. The firm's required return on equity is 8% pa.
The firm is thinking about reducing its future dividend payments by 10% so that it can use the extra cash to invest in more projects which are expected to return 8% pa, and have the same risk as the existing projects. Therefore, next year's dividend will be $0.90. No new equity or debt will be issued to fund the new projects, they'll all be funded by the cut in dividends.
What will be the stock's new annual capital return (proportional increase in price per year) if the change in payout policy goes ahead?
Assume that payout policy is irrelevant to firm value (so there's no signalling effects) and that all rates are effective annual rates.
Total cash flows can be broken into income and capital cash flows.
What is the name given to the cash flow generated from selling shares at a higher price than they were bought?
The perpetuity with growth formula, also known as the dividend discount model (DDM) or Gordon growth model, is appropriate for valuing a company's shares. ##P_0## is the current share price, ##C_1## is next year's expected dividend, ##r## is the total required return and ##g## is the expected growth rate of the dividend.
###P_0=\dfrac{C_1}{r-g}###
The below graph shows the expected future price path of the company's shares. Which of the following statements about the graph is NOT correct?

Question 543 price gains and returns over time, IRR, NPV, income and capital returns, effective return
For an asset price to triple every 5 years, what must be the expected future capital return, given as an effective annual rate?
Question 546 income and capital returns, interest only loan, no explanation
Which of the following statements about the capital and income returns of an interest-only loan is correct?
Assume that the yield curve (which shows total returns over different maturities) is flat and is not expected to change.
An interest-only loan's expected:
An investor bought a 10 year 2.5% pa fixed coupon government bond priced at par. The face value is $100. Coupons are paid semi-annually and the next one is in 6 months.
Six months later, just after the coupon at that time was paid, yields suddenly and unexpectedly fell to 2% pa. Note that all yields above are given as APR's compounding semi-annually.
What was the bond investors' historical total return over that first 6 month period, given as an effective semi-annual rate?
Question 728 inflation, real and nominal returns and cash flows, income and capital returns, no explanation
Which of the following statements about gold is NOT correct? Assume that the gold price increases by inflation. Gold has a:
An Apple (NASDAQ:AAPL) stock was purchased by an investor for $120 and one year later was sold for $150. A dividend of $4 was also collected at the end of the year just before the stock was sold.
Which of the following statements about the stock investment is NOT correct? Ignore taxes.
Over the year, the investor made a:
.
Question 748 income and capital returns, DDM, ex dividend date
A stock will pay you a dividend of $2 tonight if you buy it today.
Thereafter the annual dividend is expected to grow by 3% pa, so the next dividend after the $2 one tonight will be $2.06 in one year, then in two years it will be $2.1218 and so on. The stock's required return is 8% pa.
What is the stock price today and what do you expect the stock price to be tomorrow, approximately?
Question 744 income and capital returns, real and nominal returns and cash flows, inflation
If someone says "my shares rose by 10% last year", what do you assume that they mean? The effective annual:
A share’s current price is $60. It’s expected to pay a dividend of $1.50 in one year. The growth rate of the dividend is 0.5% pa and the stock’s required total return is 3% pa. The stock’s price can be modeled using the dividend discount model (DDM):
##P_0=\dfrac{C_1}{r-g}##
Which of the following methods is NOT equal to the stock’s expected price in one year and six months (t=1.5 years)? Note that the symbolic formulas shown in each line below do equal the formulas with numbers. The formula is just repeated with symbols and then numbers in case it helps you to identify the incorrect statement more quickly.
In the dividend discount model (DDM), share prices fall when dividends are paid. Let the high price before the fall be called the peak, and the low price after the fall be called the trough.
###P_0=\dfrac{C_1}{r-g}###
Which of the following statements about the DDM is NOT correct?
A wholesale glass importer offers credit to its customers. Customers are given 30 days to pay for their goods, but if they pay within 5 days they will get a 1% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 5th day or the 30th day. All rates given below are effective annual rates.
You just bought $100,000 worth of inventory from a wholesale supplier. You are given the option of paying within 5 days and receiving a 2% discount, or paying the full price within 60 days.
You actually don't have the cash to pay within 5 days, but you could borrow it from the bank (as an overdraft) at 10% pa, given as an effective annual rate.
In 60 days you will have enough money to pay the full cost without having to borrow from the bank.
What is the implicit interest rate charged by the wholesale supplier, given as an effective annual rate? Also, should you borrow from the bank in 5 days to pay the supplier and receive the discount? Or just pay the full price on the last possible date?
Assume that there are 365 days per year.
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $100m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $112m | Firm free cash flow or cash flow from assets (includes interest tax shields) |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 7% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 6.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 9% pa | Cost of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with constant annual perpetual cash flows from assets. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. Both the operating and firm free cash flows are constant (but not equal to each other).
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $48.5m | Operating free cash flow |
| ##\text{FFCF or CFFA}## | $50m | Firm free cash flow or cash flow from assets |
| ##g## | 0% pa | Growth rate of OFCF and FFCF |
| ##\text{WACC}_\text{BeforeTax}## | 10% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 9.7% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Cost of debt |
| ##r_\text{EL}## | 11.25% pa | Cost of levered equity |
| ##D/V_L## | 20% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
What is the value of the levered firm including interest tax shields?
Use the below information to value a levered company with annual perpetual cash flows from assets that grow. The next cash flow will be generated in one year from now. Note that ‘k’ means kilo or 1,000. So the $30k is $30,000.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}## | $30k | Operating free cash flow |
| ##g## | 1.5% pa | Growth rate of OFCF |
| ##r_\text{D}## | 4% pa | Cost of debt |
| ##r_\text{EL}## | 16.3% pa | Cost of levered equity |
| ##D/V_L## | 80% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##t_c## | 30% | Corporate tax rate |
| ##n_\text{shares}## | 100k | Number of shares |
Which of the following statements is NOT correct?
When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.
Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).
In approximately how many years will the company's total dividends be as large as the country's GDP?
Question 548 equivalent annual cash flow, time calculation, no explanation
An Apple iPhone 6 smart phone can be bought now for $999. An Android Kogan Agora 4G+ smart phone can be bought now for $240.
If the Kogan phone lasts for one year, approximately how long must the Apple phone last for to have the same equivalent annual cost?
Assume that both phones have equivalent features besides their lifetimes, that both are worthless once they've outlasted their life, the discount rate is 10% pa given as an effective annual rate, and there are no extra costs or benefits from either phone.
Question 935 real estate, NPV, perpetuity with growth, multi stage growth model, DDM
You're thinking of buying an investment property that costs $1,000,000. The property's rent revenue over the next year is expected to be $50,000 pa and rent expenses are $20,000 pa, so net rent cash flow is $30,000. Assume that net rent is paid annually in arrears, so this next expected net rent cash flow of $30,000 is paid one year from now.
The year after, net rent is expected to fall by 2% pa. So net rent at year 2 is expected to be $29,400 (=30,000*(1-0.02)^1).
The year after that, net rent is expected to rise by 1% pa. So net rent at year 3 is expected to be $29,694 (=30,000*(1-0.02)^1*(1+0.01)^1).
From year 3 onwards, net rent is expected to rise at 2.5% pa forever. So net rent at year 4 is expected to be $30,436.35 (=30,000*(1-0.02)^1*(1+0.01)^1*(1+0.025)^1).
Assume that the total required return on your investment property is 6% pa. Ignore taxes. All returns are given as effective annual rates.
What is the net present value (NPV) of buying the investment property?
Stocks in the United States usually pay quarterly dividends. For example, the retailer Wal-Mart Stores paid a $0.47 dividend every quarter over the 2013 calendar year and plans to pay a $0.48 dividend every quarter over the 2014 calendar year.
Using the dividend discount model and net present value techniques, calculate the stock price of Wal-Mart Stores assuming that:
- The time now is the beginning of January 2014. The next dividend of $0.48 will be received in 3 months (end of March 2014), with another 3 quarterly payments of $0.48 after this (end of June, September and December 2014).
- The quarterly dividend will increase by 2% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in 2015 will be $0.4896 (##=0.48×(1+0.02)^1##), with the first at the end of March 2015 and the last at the end of December 2015. In 2016 each quarterly dividend will be $0.499392 (##=0.48×(1+0.02)^2##), with the first at the end of March 2016 and the last at the end of December 2016, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- All cash flows and rates are nominal. Inflation is 3% pa.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
Stocks in the United States usually pay quarterly dividends. For example, the software giant Microsoft paid a $0.23 dividend every quarter over the 2013 financial year and plans to pay a $0.28 dividend every quarter over the 2014 financial year.
Using the dividend discount model and net present value techniques, calculate the stock price of Microsoft assuming that:
- The time now is the beginning of July 2014. The next dividend of $0.28 will be received in 3 months (end of September 2014), with another 3 quarterly payments of $0.28 after this (end of December 2014, March 2015 and June 2015).
- The quarterly dividend will increase by 2.5% every year, but each quarterly dividend over the year will be equal. So each quarterly dividend paid in the financial year beginning in September 2015 will be $ 0.287 ##(=0.28×(1+0.025)^1)##, with the last at the end of June 2016. In the next financial year beginning in September 2016 each quarterly dividend will be $0.294175 ##(=0.28×(1+0.025)^2)##, with the last at the end of June 2017, and so on forever.
- The total required return on equity is 6% pa.
- The required return and growth rate are given as effective annual rates.
- Dividend payment dates and ex-dividend dates are at the same time.
- Remember that there are 4 quarters in a year and 3 months in a quarter.
What is the current stock price?
You are an equities analyst trying to value the equity of the Australian supermarket conglomerate Woolworths, with ticker WOW. In Australia, listed companies like Woolworths tend to pay dividends every 6 months. The payment around September is the final dividend and the payment around March is called the interim dividend. Both occur annually.
- Today is mid-November 2018.
- WOW's last final dividend of $0.50 was two months ago in mid-September 2018.
- WOW's last interim dividend of $0.43 was eight months ago in mid-March 2018.
- Judging by the dividend history and WOW's prospects, you judge that the growth rate in the dividends will be 3% pa forever.
- Assume that WOW's total cost of equity is 6.5% pa. All rates are quoted as nominal effective rates.
- The dividends are nominal cash flows and the inflation rate is 2.5% pa.
What should be the current share price of WOW?
For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?
Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.
A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:
Which of the following companies is most suitable for valuation using PE multiples techniques?
A mature firm has constant expected future earnings and dividends. Both amounts are equal. So earnings and dividends are expected to be equal and unchanging.
Which of the following statements is NOT correct?
A firm has 1 million shares which trade at a price of $30 each. The firm is expected to announce earnings of $3 million at the end of the year and pay an annual dividend of $1.50 per share.
What is the firm's (forward looking) price/earnings (PE) ratio?
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.

What was CBA's backwards-looking price-earnings ratio?
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.
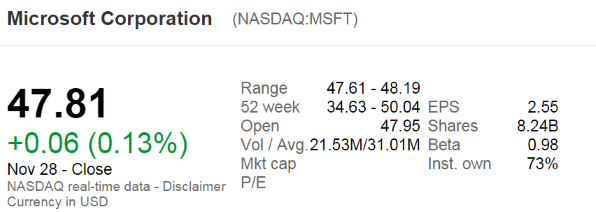
What was MSFT's backwards-looking price-earnings ratio?
A firm has 2m shares and a market capitalisation of equity of $30m. The firm just announced earnings of $5m and paid an annual dividend of $0.75 per share.
What is the firm's (backward looking) price/earnings (PE) ratio?
A 2 year government bond yields 5% pa with a coupon rate of 6% pa, paid semi-annually.
Find the effective six month rate, effective annual rate and the effective daily rate. Assume that each month has 30 days and that there are 360 days in a year.
All answers are given in the same order:
##r_\text{eff semi-annual}##, ##r_\text{eff yrly}##, ##r_\text{eff daily}##.
How much more can you borrow using an interest-only loan compared to a 25-year fully amortising loan if interest rates are 6% pa compounding per month and are not expected to change? If it makes it easier, assume that you can afford to pay $2,000 per month on either loan. Express your answer as a proportional increase using the following formula:
###\text{Proportional Increase} = \dfrac{V_\text{0,interest only}}{V_\text{0,fully amortising}} - 1###Which of the following interest rate quotes is NOT equivalent to a 10% effective annual rate of return? Assume that each year has 12 months, each month has 30 days, each day has 24 hours, each hour has 60 minutes and each minute has 60 seconds. APR stands for Annualised Percentage Rate.
A home loan company advertises an interest rate of 4.5% pa, payable monthly. Which of the following statements about the interest rate is NOT correct?
You just spent $1,000 on your credit card. The interest rate is 24% pa compounding monthly. Assume that your credit card account has no fees and no minimum monthly repayment.
If you can't make any interest or principal payments on your credit card debt over the next year, how much will you owe one year from now?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What will be the price of the stock in four and a half years (t = 4.5)?
When using the dividend discount model to price a stock:
### p_{0} = \frac{d_1}{r - g} ###
The growth rate of dividends (g):
A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock is 10% pa, given as an effective annual rate.
What is the price of the share now?
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 8 | 8 | 8 | 20 | 8 | ... |
After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. Note that the $8 dividend at time zero is about to be paid tonight.
What will be the price of the stock in 5 years (t = 5), just after the dividend at that time has been paid?
The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:
###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###
###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###
For a firm with debt, what is the amount of the interest tax shield per year?
Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.
For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.
The advantage of negative gearing is an example of the benefits of:
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.

What was MSFT's market capitalisation of equity?
Question 452 limited liability, expected and historical returns
What is the lowest and highest expected share price and expected return from owning shares in a company over a finite period of time?
Let the current share price be ##p_0##, the expected future share price be ##p_1##, the expected future dividend be ##d_1## and the expected return be ##r##. Define the expected return as:
##r=\dfrac{p_1-p_0+d_1}{p_0} ##
The answer choices are stated using inequalities. As an example, the first answer choice "(a) ##0≤p<∞## and ##0≤r< 1##", states that the share price must be larger than or equal to zero and less than positive infinity, and that the return must be larger than or equal to zero and less than one.
Government bonds currently have a return of 5% pa. A stock has an expected return of 6% pa and the market return is 7% pa. What is the beta of the stock?
Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?
| Portfolio Details | ||||||
| Stock | Expected return |
Standard deviation |
Correlation | Beta | Dollars invested |
|
| A | 0.2 | 0.4 | 0.12 | 0.5 | 40 | |
| B | 0.3 | 0.8 | 1.5 | 80 | ||
What is the beta of the above portfolio?
Fundamentalists who analyse company financial reports and news announcements (but who don't have inside information) will make positive abnormal returns if:
A stock is expected to pay the following dividends:
| Cash Flows of a Stock | ||||||
| Time (yrs) | 0 | 1 | 2 | 3 | 4 | ... |
| Dividend ($) | 0.00 | 1.15 | 1.10 | 1.05 | 1.00 | ... |
After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,
- the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
- the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.
The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.
What is the current price of the stock?
Currently, a mining company has a share price of $6 and pays constant annual dividends of $0.50. The next dividend will be paid in 1 year. Suddenly and unexpectedly the mining company announces that due to higher than expected profits, all of these windfall profits will be paid as a special dividend of $0.30 in 1 year.
If investors believe that the windfall profits and dividend is a one-off event, what will be the new share price? If investors believe that the additional dividend is actually permanent and will continue to be paid, what will be the new share price? Assume that the required return on equity is unchanged. Choose from the following, where the first share price includes the one-off increase in earnings and dividends for the first year only ##(P_\text{0 one-off})## , and the second assumes that the increase is permanent ##(P_\text{0 permanent})##:
Note: When a firm makes excess profits they sometimes pay them out as special dividends. Special dividends are just like ordinary dividends but they are one-off and investors do not expect them to continue, unlike ordinary dividends which are expected to persist.
A very low-risk stock just paid its semi-annual dividend of $0.14, as it has for the last 5 years. You conservatively estimate that from now on the dividend will fall at a rate of 1% every 6 months.
If the stock currently sells for $3 per share, what must be its required total return as an effective annual rate?
If risk free government bonds are trading at a yield of 4% pa, given as an effective annual rate, would you consider buying or selling the stock?
The stock's required total return is:
A share just paid its semi-annual dividend of $5. The dividend is expected to grow at 1% every 6 months forever. This 1% growth rate is an effective 6 month rate.
Therefore the next dividend will be $5.05 in six months. The required return of the stock 8% pa, given as an effective annual rate.
What is the price of the share now?
In the dividend discount model:
### P_0= \frac{d_1}{r-g} ###
The pronumeral ##g## is supposed to be the:
A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the end-of-year amount, paid at the end of every year.
This fee is charged regardless of whether the fund makes gains or losses on your money.
The fund offers to invest your money in shares which have an expected return of 10% pa before fees.
You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.
How much money do you expect to have in the fund in 40 years? Also, what is the future value of the fees that the fund expects to earn from you? Give both amounts as future values in 40 years. Assume that:
- The fund has no private information.
- Markets are weak and semi-strong form efficient.
- The fund's transaction costs are negligible.
- The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.
- The fund invests its fees in the same companies as it invests your funds in, but with no fees.
The below answer choices list your expected wealth in 40 years and then the fund's expected wealth in 40 years.
A company advertises an investment costing $1,000 which they say is underpriced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Assume that there are no dividend payments so the entire 15% total return is all capital return.
Assuming that the company's statements are correct, what is the NPV of buying the investment if the 15% return lasts for the next 100 years (t=0 to 100), then reverts to 10% pa after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant. All returns are given as effective annual rates.
The answer choices below are given in the same order (15% for 100 years, and 15% forever):
What type of present value equation is best suited to value a residential house investment property that is expected to pay constant rental payments forever? Note that 'constant' has the same meaning as 'level' in this context.
A firm is considering a business project which costs $11m now and is expected to pay a constant $1m at the end of every year forever.
Assume that the initial $11m cost is funded using the firm's existing cash so no new equity or debt will be raised. The cost of capital is 10% pa.
Which of the following statements about net present value (NPV), internal rate of return (IRR) and payback period is NOT correct?
Question 780 mispriced asset, NPV, DDM, market efficiency, no explanation
A company advertises an investment costing $1,000 which they say is under priced. They say that it has an expected total return of 15% pa, but a required return of only 10% pa. Of the 15% pa total expected return, the dividend yield is expected to be 4% pa and the capital yield 11% pa. Assume that the company's statements are correct.
What is the NPV of buying the investment if the 15% total return lasts for the next 100 years (t=0 to 100), then reverts to 10% after that time? Also, what is the NPV of the investment if the 15% return lasts forever?
In both cases, assume that the required return of 10% remains constant, the dividends can only be re-invested at 10% pa and all returns are given as effective annual rates. The answer choices below are given in the same order (15% for 100 years, and 15% forever):
Question 241 Miller and Modigliani, leverage, payout policy, diversification, NPV
One of Miller and Modigliani's (M&M's) important insights is that a firm's managers should not try to achieve a particular level of leverage in a world with zero taxes and perfect information since investors can make their own leverage. Therefore corporate capital structure policy is irrelevant since investors can achieve their own desired leverage at the personal level by borrowing or lending on their own.
This principal of 'home-made' or 'do-it-yourself' leverage can also be applied to other topics. Read the following statements to decide which are true:
(I) Payout policy: a firm's managers should not try to achieve a particular pattern of equity payout.
(II) Agency costs: a firm's managers should not try to minimise agency costs.
(III) Diversification: a firm's managers should not try to diversify across industries.
(IV) Shareholder wealth: a firm's managers should not try to maximise shareholders' wealth.
Which of the above statement(s) are true?
The average weekly earnings of an Australian adult worker before tax was $1,542.40 per week in November 2014 according to the Australian Bureau of Statistics. Therefore average annual earnings before tax were $80,204.80 assuming 52 weeks per year. Personal income tax rates published by the Australian Tax Office are reproduced for the 2014-2015 financial year in the table below:
| Taxable income | Tax on this income |
|---|---|
| 0 – $18,200 | Nil |
| $18,201 – $37,000 | 19c for each $1 over $18,200 |
| $37,001 – $80,000 | $3,572 plus 32.5c for each $1 over $37,000 |
| $80,001 – $180,000 | $17,547 plus 37c for each $1 over $80,000 |
| $180,001 and over | $54,547 plus 45c for each $1 over $180,000 |
The above rates do not include the Medicare levy of 2%. Exclude the Medicare levy from your calculations
How much personal income tax would you have to pay per year if you earned $80,204.80 per annum before-tax?
Question 449 personal tax on dividends, classical tax system
A small private company has a single shareholder. This year the firm earned a $100 profit before tax. All of the firm's after tax profits will be paid out as dividends to the owner.
The corporate tax rate is 30% and the sole shareholder's personal marginal tax rate is 45%.
The United States' classical tax system applies because the company generates all of its income in the US and pays corporate tax to the Internal Revenue Service. The shareholder is also an American for tax purposes.
What will be the personal tax payable by the shareholder and the corporate tax payable by the company?
Question 448 franking credit, personal tax on dividends, imputation tax system
A small private company has a single shareholder. This year the firm earned a $100 profit before tax. All of the firm's after tax profits will be paid out as dividends to the owner.
The corporate tax rate is 30% and the sole shareholder's personal marginal tax rate is 45%.
The Australian imputation tax system applies because the company generates all of its income in Australia and pays corporate tax to the Australian Tax Office. Therefore all of the company's dividends are fully franked. The sole shareholder is an Australian for tax purposes and can therefore use the franking credits to offset his personal income tax liability.
What will be the personal tax payable by the shareholder and the corporate tax payable by the company?
A mining firm has just discovered a new mine. So far the news has been kept a secret.
The net present value of digging the mine and selling the minerals is $250 million, but $500 million of new equity and $300 million of new bonds will need to be issued to fund the project and buy the necessary plant and equipment.
The firm will release the news of the discovery and equity and bond raising to shareholders simultaneously in the same announcement. The shares and bonds will be issued shortly after.
Once the announcement is made and the new shares and bonds are issued, what is the expected increase in the value of the firm's assets ##(\Delta V)##, market capitalisation of debt ##(\Delta D)## and market cap of equity ##(\Delta E)##? Assume that markets are semi-strong form efficient.
The triangle symbol ##\Delta## is the Greek letter capital delta which means change or increase in mathematics.
Ignore the benefit of interest tax shields from having more debt.
Remember: ##\Delta V = \Delta D+ \Delta E##
Question 625 dividend re-investment plan, capital raising
Which of the following statements about dividend re-investment plans (DRP's) is NOT correct?
In late 2003 the listed bank ANZ announced a 2-for-11 rights issue to fund the takeover of New Zealand bank NBNZ. Below is the chronology of events:
- 23/10/2003. Share price closes at $18.30.
- 24/10/2003. 2-for-11 rights issue announced at a subscription price of $13. The proceeds of the rights issue will be used to acquire New Zealand bank NBNZ. Trading halt announced in morning before market opens.
- 28/10/2003. Trading halt lifted. Last (and only) day that shares trade cum-rights. Share price opens at $18.00 and closes at $18.14.
- 29/10/2003. Shares trade ex-rights.
All things remaining equal, what would you expect ANZ's stock price to open at on the first day that it trades ex-rights (29/10/2003)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
In mid 2009 the listed mining company Rio Tinto announced a 21-for-40 renounceable rights issue. Below is the chronology of events:
- 04/06/2009. Share price opens at $69.00 and closes at $66.90.
- 05/06/2009. 21-for-40 rights issue announced at a subscription price of $28.29.
- 16/06/2009. Last day that shares trade cum-rights. Share price opens at $76.40 and closes at $75.50.
- 17/06/2009. Shares trade ex-rights. Rights trading commences.
All things remaining equal, what would you expect Rio Tinto's stock price to open at on the first day that it trades ex-rights (17/6/2009)? Ignore the time value of money since time is negligibly short. Also ignore taxes.
Question 513 stock split, reverse stock split, stock dividend, bonus issue, rights issue
Which of the following statements is NOT correct?
Question 566 capital structure, capital raising, rights issue, on market repurchase, dividend, stock split, bonus issue
A company's share price fell by 20% and its number of shares rose by 25%. Assume that there are no taxes, no signalling effects and no transaction costs.
Which one of the following corporate events may have happened?
A company conducts a 2 for 3 rights issue at a subscription price of $8 when the pre-announcement stock price was $9. Assume that all investors use their rights to buy those extra shares.
What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A firm wishes to raise $100 million now. The firm's current market value of equity is $300m and the market price per share is $5. They estimate that they'll be able to issue shares in a rights issue at a subscription price of $4. All answers are rounded to 6 decimal places. Ignore the time value of money and assume that all shareholders exercise their rights. Which of the following statements is NOT correct?
Question 803 capital raising, rights issue, initial public offering, on market repurchase, no explanation
Which one of the following capital raisings or payouts involve the sale of shares to existing shareholders only?
A firm is about to conduct a 2-for-7 rights issue with a subscription price of $10 per share. They haven’t announced the capital raising to the market yet and the share price is currently $13 per share. Assume that every shareholder will exercise their rights, the cash raised will simply be put in the bank, and the rights issue is completed so quickly that the time value of money can be ignored. Disregard signalling, taxes and agency-related effects.
Which of the following statements about the rights issue is NOT correct? After the rights issue is completed:
A company conducts a 4 for 3 stock split. What is the percentage change in the stock price and the number of shares outstanding? The answers are given in the same order.
A company conducts a 10 for 3 stock split. What is the percentage increase in the stock price and the number of shares outstanding? The answers are given in the same order.
A firm conducts a two-for-one stock split. Which of the following consequences would NOT be expected?
Which one of the following statements is NOT correct? A 1-for-4 bonus issue:
When someone says that they're "buying American dollars" (USD), what type of asset are they probably buying? They're probably buying:
An Indonesian lady wishes to convert 1 million Indonesian rupiah (IDR) to Australian dollars (AUD). Exchange rates are 13,125 IDR per USD and 0.79 USD per AUD. How many AUD is the IDR 1 million worth?
Question 315 foreign exchange rate, American and European terms
If the current AUD exchange rate is USD 0.9686 = AUD 1, what is the European terms quote of the AUD against the USD?
Question 319 foreign exchange rate, monetary policy, American and European terms
Investors expect the Reserve Bank of Australia (RBA) to keep the policy rate steady at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 25 basis points due to fears that the economy is growing too fast and that inflation will be above their target rate of 2 to 3 per cent.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:
Question 321 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will increase the policy rate by 50 basis points due to high future GDP and inflation forecasts.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar will:
Question 626 cross currency interest rate parity, foreign exchange rate, forward foreign exchange rate
The Australian cash rate is expected to be 2% pa over the next one year, while the Japanese cash rate is expected to be 0% pa, both given as nominal effective annual rates. The current exchange rate is 100 JPY per AUD.
What is the implied 1 year forward foreign exchange rate?
Question 245 foreign exchange rate, monetary policy, foreign exchange rate direct quote, no explanation
Investors expect Australia's central bank, the RBA, to leave the policy rate unchanged at their next meeting.
Then unexpectedly, the policy rate is reduced due to fears that Australia's GDP growth is slowing.
What do you expect to happen to Australia's exchange rate? Direct and indirect quotes are given from the perspective of an Australian.
The Australian dollar will:
Question 606 foreign exchange rate, American and European terms
Which of the following FX quotes (current in October 2015) is given in American terms?
The Australian dollar's value was:
Did the Australian dollar or against the US dollar between these dates?
Which of the following quantities is commonly assumed to be normally distributed?
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Which of the below statements is NOT correct?
The symbol ##\text{GDR}_{0\rightarrow 1}## represents a stock's gross discrete return per annum over the first year. ##\text{GDR}_{0\rightarrow 1} = P_1/P_0##. The subscript indicates the time period that the return is mentioned over. So for example, ##\text{AAGDR}_{1 \rightarrow 3}## is the arithmetic average GDR measured over the two year period from years 1 to 3, but it is expressed as a per annum rate.
Which of the below statements about the arithmetic and geometric average GDR is NOT correct?
Question 811 log-normal distribution, mean and median returns, return distribution, arithmetic and geometric averages
Which of the following statements about probability distributions is NOT correct?
Question 721 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some Commonwealth Bank (CBA) shares. He has calculated CBA’s monthly returns for each month in the past 20 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 1% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.01=1\% \text{ per month}###He also found the standard deviation of these monthly returns which was 5% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.05=5\%\text{ per month}###Which of the below statements about Fred’s CBA shares is NOT correct? Assume that the past historical average return is the true population average of future expected returns.
Government bonds currently have a return of 5%. A stock has a beta of 2 and the market return is 7%. What is the expected return of the stock?
Treasury bonds currently have a return of 5% pa. A stock has a beta of 0.5 and the market return is 10% pa. What is the expected return of the stock?
A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.
The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.
The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.
What is the firm's after-tax WACC? Assume a classical tax system.
According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?
Which statement(s) are correct?
(i) All stocks that plot on the Security Market Line (SML) are fairly priced.
(ii) All stocks that plot above the Security Market Line (SML) are overpriced.
(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.
Select the most correct response:
A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?
A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.
According to the Capital Asset Pricing Model (CAPM), which statement is correct?
Question 104 CAPM, payout policy, capital structure, Miller and Modigliani, risk
Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.
For a firm operating in this perfect world, which statement(s) are correct?
(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.
(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.
(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.
Select the most correct response:
The security market line (SML) shows the relationship between beta and expected return.
Buying investment projects that plot above the SML would lead to:
According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?
Question 235 SML, NPV, CAPM, risk
The security market line (SML) shows the relationship between beta and expected return.
Investment projects that plot on the SML would have:
Question 244 CAPM, SML, NPV, risk
Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:
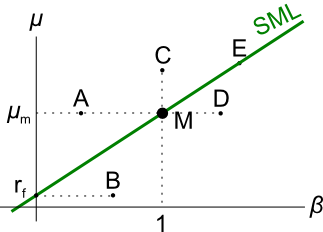
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?
The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):
###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###
Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:
###r_\text{total}=r_\text{income}+r_\text{capital}###
So the total return of an asset is the income component plus the capital or price growth component.
Another way to break up total return is to use the Capital Asset Pricing Model:
###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###
###r_\text{total}=r_\text{time value}+r_\text{risk premium}###
So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.
Using the above theory and your general knowledge, which of the below equations, if any, are correct?
(I) ##r_\text{income}=r_\text{time value}##
(II) ##r_\text{income}=r_\text{risk premium}##
(III) ##r_\text{capital}=r_\text{time value}##
(IV) ##r_\text{capital}=r_\text{risk premium}##
(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##
Which of the equations are correct?
Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?
Due to floods overseas, there is a cut in the supply of the mineral iron ore and its price increases dramatically. An Australian iron ore mining company therefore expects a large but temporary increase in its profit and cash flows. The mining company does not have any positive NPV projects to begin, so what should it do? Select the most correct answer.
A newly floated farming company is financed with senior bonds, junior bonds, cumulative non-voting preferred stock and common stock. The new company has no retained profits and due to floods it was unable to record any revenues this year, leading to a loss. The firm is not bankrupt yet since it still has substantial contributed equity (same as paid-up capital).
On which securities must it pay interest or dividend payments in this terrible financial year?
An equity index is currently at 5,000 points. The 2 year futures price is 5,400 points and the total required return is 8% pa with continuous compounding. Each index point is worth $25.
What is the implied continuous dividend yield as a continuously compounded rate per annum?
A stock is expected to pay a dividend of $5 per share in 1 month and $5 again in 7 months.
The stock price is $100, and the risk-free rate of interest is 10% per annum with continuous compounding. The yield curve is flat. Assume that investors are risk-neutral.
An investor has just taken a short position in a one year forward contract on the stock.
Find the forward price ##(F_1)## and value of the contract ##(V_0)## initially. Also find the value of the short futures contract in 6 months ##(V_\text{0.5, SF})## if the stock price fell to $90.
A $100 stock has a continuously compounded expected total return of 10% pa. Its dividend yield is 2% pa with continuous compounding. What do you expect its price to be in one year?
A $100 stock has a continuously compounded expected total return of 10% pa. Its dividend yield is 2% pa with continuous compounding. What do you expect its price to be in 2.5 years?
Question 320 foreign exchange rate, monetary policy, American and European terms
Investors expect the Reserve Bank of Australia (RBA) to decrease the overnight cash rate at their next meeting.
Then unexpectedly, the RBA announce that they will keep the policy rate unchanged.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar is likely to:
Question 322 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to decrease the policy rate by 25 basis points at their next meeting.
Then unexpectedly, the RBA announce that they will decrease the policy rate by 50 basis points due to fears of a recession and deflation.
What do you expect to happen to Australia's exchange rate? The Australian dollar will:
Question 323 foreign exchange rate, monetary policy, American and European terms
The market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting.
As expected, the RBA increases the policy rate by 25 basis points.
What do you expect to happen to Australia's exchange rate in the short term? The Australian dollar will:
In the 1997 Asian financial crisis many countries' exchange rates depreciated rapidly against the US dollar (USD). The Thai, Indonesian, Malaysian, Korean and Filipino currencies were severely affected. The below graph shows these Asian countries' currencies in USD per one unit of their currency, indexed to 100 in June 1997.
Of the statements below, which is NOT correct? The Asian countries':
An American wishes to convert USD 1 million to Australian dollars (AUD). The exchange rate is 0.8 USD per AUD. How much is the USD 1 million worth in AUD?
A Chinese man wishes to convert AUD 1 million into Chinese Renminbi (RMB, also called the Yuan (CNY)). The exchange rate is 6.35 RMB per USD, and 0.72 USD per AUD. How much is the AUD 1 million worth in RMB?
Question 335 foreign exchange rate, American and European terms
Investors expect Australia's central bank, the RBA, to reduce the policy rate at their next meeting due to fears that the economy is slowing. Then unexpectedly, the policy rate is actually kept unchanged.
What do you expect to happen to Australia's exchange rate?
Question 667 forward foreign exchange rate, foreign exchange rate, cross currency interest rate parity, no explanation
The Australian cash rate is expected to be 2% pa over the next one year, while the US cash rate is expected to be 0% pa, both given as nominal effective annual rates. The current exchange rate is 0.73 USD per AUD.
What is the implied 1 year USD per AUD forward foreign exchange rate?
Question 888 foreign exchange rate, speculation, no explanation
The current Australian exchange rate is 0.8 USD per AUD.
If you think that the AUD will depreciate against the USD, contrary to the rest of the market, how could you profit? Right now you should:
Question 891 foreign exchange rate, monetary policy, no explanation
Suppose the market expects the Bank of Japan (BoJ) to decrease their short term interest rate by 15 basis points at their next meeting. The current short term interest rate is -0.1% pa and the exchange rate is 100 JPY per USD.
Then unexpectedly, the BoJ announce that they will leave the short term interest rate unchanged.
What do you expect to happen to Japan’s exchange rate on the day when the surprise announcement is made? The Japanese Yen (JPY) is likely to suddenly:
Question 924 foreign exchange rate, forward foreign exchange rate, arbitrage, forward interest rate, no explanation
Suppose that the yield curve in the United States of America and Australia is flat and that the current:
- USD federal funds rate is 1% pa;
- AUD cash rate is 1.5% pa;
- Spot AUD exchange rate is 1 USD per AUD;
- One year forward AUD exchange rate is 0.97 USD per AUD.
You suspect that there’s an arbitrage opportunity.
Which one of the following statements about the potential arbitrage opportunity is NOT correct?
An equity index is currently at 5,200 points. The 6 month futures price is 5,300 points and the total required return is 6% pa with continuous compounding. Each index point is worth $25.
What is the implied dividend yield as a continuously compounded rate per annum?
An equity index is currently at 4,800 points. The 1.5 year futures price is 5,100 points and the total required return is 6% pa with continuous compounding. Each index point is worth $25.
What is the implied dividend yield as a continuously compounded rate per annum?
Question 719 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed. The graph below summarises this information and provides some helpful formulas.

In one year, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 720 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
A stock has an arithmetic average continuously compounded return (AALGDR) of 10% pa, a standard deviation of continuously compounded returns (SDLGDR) of 80% pa and current stock price of $1. Assume that stock prices are log-normally distributed.
In 5 years, what do you expect the median and mean prices to be? The answer options are given in the same order.
Question 723 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Here is a table of stock prices and returns. Which of the statements below the table is NOT correct?
| Price and Return Population Statistics | ||||
| Time | Prices | LGDR | GDR | NDR |
| 0 | 100 | |||
| 1 | 99 | -0.010050 | 0.990000 | -0.010000 |
| 2 | 180.40 | 0.600057 | 1.822222 | 0.822222 |
| 3 | 112.73 | 0.470181 | 0.624889 | 0.375111 |
| Arithmetic average | 0.0399 | 1.1457 | 0.1457 | |
| Arithmetic standard deviation | 0.4384 | 0.5011 | 0.5011 | |
Question 779 mean and median returns, return distribution, arithmetic and geometric averages, continuously compounding rate
Fred owns some BHP shares. He has calculated BHP’s monthly returns for each month in the past 30 years using this formula:
###r_\text{t monthly}=\ln \left( \dfrac{P_t}{P_{t-1}} \right)###He then took the arithmetic average and found it to be 0.8% per month using this formula:
###\bar{r}_\text{monthly}= \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( r_\text{t monthly} \right)} }{T} =0.008=0.8\% \text{ per month}###He also found the standard deviation of these monthly returns which was 15% per month:
###\sigma_\text{monthly} = \dfrac{ \displaystyle\sum\limits_{t=1}^T{\left( \left( r_\text{t monthly} - \bar{r}_\text{monthly} \right)^2 \right)} }{T} =0.15=15\%\text{ per month}###Assume that the past historical average return is the true population average of future expected returns and the stock's returns calculated above ##(r_\text{t monthly})## are normally distributed. Which of the below statements about Fred’s BHP shares is NOT correct?
If a variable, say X, is normally distributed with mean ##\mu## and variance ##\sigma^2## then mathematicians write ##X \sim \mathcal{N}(\mu, \sigma^2)##.
If a variable, say Y, is log-normally distributed and the underlying normal distribution has mean ##\mu## and variance ##\sigma^2## then mathematicians write ## Y \sim \mathbf{ln} \mathcal{N}(\mu, \sigma^2)##.
The below three graphs show probability density functions (PDF) of three different random variables Red, Green and Blue.

Select the most correct statement:
Question 907 continuously compounding rate, return types, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its continuously compounded return ##(r_{CC})## be? If the price now is ##P_0## and the price in one year is ##P_1## then the continuously compounded return over the next year is:
###r_\text{CC annual} = \ln{\left[ \dfrac{P_1}{P_0} \right]} = \text{LGDR}_\text{annual}###Question 908 effective rate, return types, gross discrete return, return distribution, price gains and returns over time
For an asset's price to double from say $1 to $2 in one year, what must its gross discrete return (GDR) be? If the price now is ##P_0## and the price in one year is ##P_1## then the gross discrete return over the next year is:
###\text{GDR}_\text{annual} = \dfrac{P_1}{P_0}###A furniture distributor offers credit to its customers. Customers are given 25 days to pay for their goods, but if they pay immediately they will get a 1% discount.
What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay either immediately or on the 25th day. All rates given below are effective annual rates.
Question 778 CML, systematic and idiosyncratic risk, portfolio risk, CAPM
The capital market line (CML) is shown in the graph below. The total standard deviation is denoted by σ and the expected return is μ. Assume that markets are efficient so all assets are fairly priced.
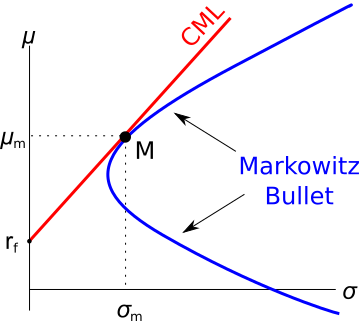
Which of the below statements is NOT correct?
In the home loan market, the acronym LVR stands for Loan to Valuation Ratio. If you bought a house worth one million dollars, partly funded by an $800,000 home loan, then your LVR was 80%. The LVR is equivalent to which of the following ratios?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
An old company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
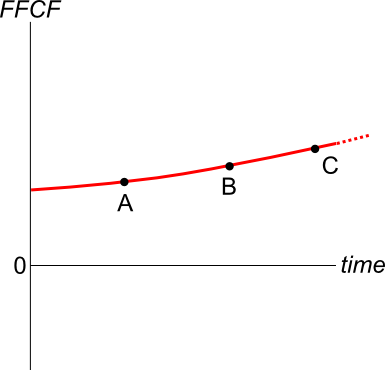
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.
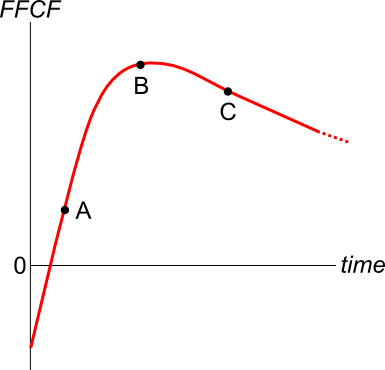
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:
###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###
Which point corresponds to the best time to calculate the terminal value?
Question 419 capital budgeting, NPV, interest tax shield, WACC, CFFA, CAPM, no explanation
| Project Data | ||
| Project life | 1 year | |
| Initial investment in equipment | $6m | |
| Depreciation of equipment per year | $6m | |
| Expected sale price of equipment at end of project | 0 | |
| Unit sales per year | 9m | |
| Sale price per unit | $8 | |
| Variable cost per unit | $6 | |
| Fixed costs per year, paid at the end of each year | $1m | |
| Interest expense in first year (at t=1) | $0.53m | |
| Tax rate | 30% | |
| Government treasury bond yield | 5% | |
| Bank loan debt yield | 6% | |
| Market portfolio return | 10% | |
| Covariance of levered equity returns with market | 0.08 | |
| Variance of market portfolio returns | 0.16 | |
| Firm's and project's debt-to-assets ratio | 50% | |
Notes
- Due to the project, current assets will increase by $5m now (t=0) and fall by $5m at the end (t=1). Current liabilities will not be affected.
Assumptions
- The debt-to-assets ratio will be kept constant throughout the life of the project. The amount of interest expense at the end of each period has been correctly calculated to maintain this constant debt-to-equity ratio.
- Millions are represented by 'm'.
- All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
- All rates and cash flows are real. The inflation rate is 2% pa.
- All rates are given as effective annual rates.
- The 50% capital gains tax discount is not available since the project is undertaken by a firm, not an individual.
What is the net present value (NPV) of the project?
Use the below information to value a mature levered company with growing annual perpetual cash flows and a constant debt-to-assets ratio. The next cash flow will be generated in one year from now, so a perpetuity can be used to value this firm. The firm's debt funding comprises annual fixed coupon bonds that all have the same seniority and coupon rate. When these bonds mature, new bonds will be re-issued, and so on in perpetuity. The yield curve is flat.
| Data on a Levered Firm with Perpetual Cash Flows | ||
| Item abbreviation | Value | Item full name |
| ##\text{OFCF}_1## | $12.5m | Operating free cash flow at time 1 |
| ##\text{FFCF}_1 \text{ or }\text{CFFA}_1## | $14m | Firm free cash flow or cash flow from assets at time 1 |
| ##\text{EFCF}_1## | $11m | Equity free cash flow at time 1 |
| ##\text{BondCoupons}_1## | $1.2m | Bond coupons paid to debt holders at time 1 |
| ##g## | 2% pa | Growth rate of OFCF, FFCF, EFCF and Debt cash flow |
| ##\text{WACC}_\text{BeforeTax}## | 9% pa | Weighted average cost of capital before tax |
| ##\text{WACC}_\text{AfterTax}## | 8.25% pa | Weighted average cost of capital after tax |
| ##r_\text{D}## | 5% pa | Bond yield |
| ##r_\text{EL}## | 13% pa | Cost or required return of levered equity |
| ##D/V_L## | 50% pa | Debt to assets ratio, where the asset value includes tax shields |
| ##n_\text{shares}## | 1m | Number of shares |
| ##t_c## | 30% | Corporate tax rate |
Which of the following statements is NOT correct?
A firm has a debt-to-equity ratio of 60%. What is its debt-to-assets ratio?
Stock A and B's returns have a correlation of 0.3. Which statement is NOT correct?
Question 308 risk, standard deviation, variance, no explanation
A stock's standard deviation of returns is expected to be:
- 0.09 per month for the first 5 months;
- 0.14 per month for the next 7 months.
What is the expected standard deviation of the stock per year ##(\sigma_\text{annual})##?
Assume that returns are independently and identically distributed (iid) and therefore have zero auto-correlation.
A stock's required total return will increase when its:
Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Assume that investors can borrow and lend at the risk free rate. Which of the below statements is NOT correct?
Which of the following is NOT a valid method for estimating the beta of a company's stock? Assume that markets are efficient, a long history of past data is available, the stock possesses idiosyncratic and market risk. The variances and standard deviations below denote total risks.
Question 800 leverage, portfolio return, risk, portfolio risk, capital structure, no explanation
Which of the following assets would you expect to have the highest required rate of return? All values are current market values.
Which of the following statements about an asset’s standard deviation of returns is NOT correct? All other things remaining equal, the higher the asset’s standard deviation of returns:
Question 576 inflation, real and nominal returns and cash flows
What is the present value of a nominal payment of $1,000 in 4 years? The nominal discount rate is 8% pa and the inflation rate is 2% pa.
Question 727 inflation, real and nominal returns and cash flows
The Australian Federal Government lends money to domestic students to pay for their university education. This is known as the Higher Education Contribution Scheme (HECS). The nominal interest rate on the HECS loan is set equal to the consumer price index (CPI) inflation rate. The interest is capitalised every year, which means that the interest is added to the principal. The interest and principal does not need to be repaid by students until they finish study and begin working.
Which of the following statements about HECS loans is NOT correct?
Question 739 real and nominal returns and cash flows, inflation
There are a number of different formulas involving real and nominal returns and cash flows. Which one of the following formulas is NOT correct? All returns are effective annual rates. Note that the symbol ##\approx## means 'approximately equal to'.
Question 992 inflation, real and nominal returns and cash flows
You currently have $100 in the bank which pays a 10% pa interest rate.
Oranges currently cost $1 each at the shop and inflation is 5% pa which is the expected growth rate in the orange price.
This information is summarised in the table below, with some parts missing that correspond to the answer options. All rates are given as effective annual rates. Note that when payments are not specified as real, as in this question, they're conventionally assumed to be nominal.
| Wealth in Dollars and Oranges | ||||
| Time (year) | Bank account wealth ($) | Orange price ($) | Wealth in oranges | |
| 0 | 100 | 1 | 100 | |
| 1 | 110 | 1.05 | (a) | |
| 2 | (b) | (c) | (d) | |
Which of the following statements is NOT correct? Your:
Question 408 leverage, portfolio beta, portfolio risk, real estate, CAPM
You just bought a house worth $1,000,000. You financed it with an $800,000 mortgage loan and a deposit of $200,000.
You estimate that:
- The house has a beta of 1;
- The mortgage loan has a beta of 0.2.
What is the beta of the equity (the $200,000 deposit) that you have in your house?
Also, if the risk free rate is 5% pa and the market portfolio's return is 10% pa, what is the expected return on equity in your house? Ignore taxes, assume that all cash flows (interest payments and rent) were paid and received at the end of the year, and all rates are effective annual rates.
A fairly priced stock has an expected return of 15% pa. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the beta of the stock?
A fairly priced stock has a beta that is the same as the market portfolio's beta. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the expected return of the stock?
A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.
What is the price of the stock now?
The CAPM can be used to find a business's expected opportunity cost of capital:
###r_i=r_f+β_i (r_m-r_f)###
What should be used as the risk free rate ##r_f##?

Assets A, B, M and ##r_f## are shown on the graphs above. Asset M is the market portfolio and ##r_f## is the risk free yield on government bonds. Which of the below statements is NOT correct?
Question 657 systematic and idiosyncratic risk, CAPM, no explanation
A stock's required total return will decrease when its:
A stock's total standard deviation of returns is 20% pa. The market portfolio's total standard deviation of returns is 15% pa. The beta of the stock is 0.8.
What is the stock's diversifiable standard deviation?
The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
A stock has a beta of 0.5.
In the last 5 minutes, the federal government unexpectedly raised taxes. Over this time the share market fell by 3%. The risk free rate was unchanged.
What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
Question 810 CAPM, systematic and idiosyncratic risk, market efficiency
Examine the graphs below. Assume that asset A is a single stock. Which of the following statements is NOT correct? Asset A:
You work for XYZ company and you’ve been asked to evaluate a new project which has double the systematic risk of the company’s other projects.
You use the Capital Asset Pricing Model (CAPM) formula and input the treasury yield ##(r_f )##, market risk premium ##(r_m-r_f )## and the company’s asset beta risk factor ##(\beta_{XYZ} )## into the CAPM formula which outputs a return.
This return that you’ve just found is:
The market's expected total return is 10% pa and the risk free rate is 5% pa, both given as effective annual rates.
A stock has a beta of 0.7.
In the last 5 minutes, bad economic news was released showing a higher chance of recession. Over this time the share market fell by 2%. The risk free rate was unchanged. What do you think was the stock's historical return over the last 5 minutes, given as an effective 5 minute rate?
A common phrase heard in financial markets is that ‘high risk investments deserve high returns’. To make this statement consistent with the Capital Asset Pricing Model (CAPM), a high amount of what specific type of risk deserves a high return?
Investors deserve high returns when they buy assets with high:
Three important classes of investable risky assets are:
- Corporate debt which has low total risk,
- Real estate which has medium total risk,
- Equity which has high total risk.
Assume that the correlation between total returns on:
- Corporate debt and real estate is 0.1,
- Corporate debt and equity is 0.1,
- Real estate and equity is 0.5.
You are considering investing all of your wealth in one or more of these asset classes. Which portfolio will give the lowest total risk? You are restricted from shorting any of these assets. Disregard returns and the risk-return trade-off, pretend that you are only concerned with minimising risk.
Question 965 foreign exchange reserve, foreign exchange rate, no explanation
Observe the below graph of Chinese foreign exchange reserves held by the central bank, as well as the Chinese currency the Yuan (CNY, also called the Renminbi, RMB) against the US Dollar. Note the inverted y-axis scale on the Yuan exchange rate graph.
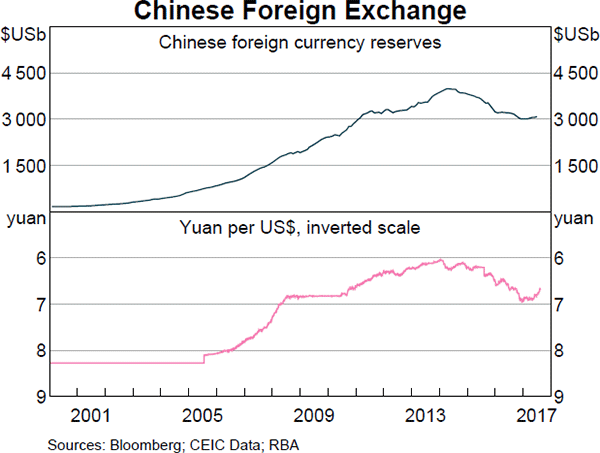
Which of the below statements is NOT correct?
Question 494 franking credit, personal tax on dividends, imputation tax system
A firm pays a fully franked cash dividend of $100 to one of its Australian shareholders who has a personal marginal tax rate of 15%. The corporate tax rate is 30%.
What will be the shareholder's personal tax payable due to the dividend payment?
You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.
How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).
A prospective home buyer can afford to pay $2,000 per month in mortgage loan repayments. The central bank recently lowered its policy rate by 0.25%, and residential home lenders cut their mortgage loan rates from 4.74% to 4.49%.
How much more can the prospective home buyer borrow now that interest rates are 4.49% rather than 4.74%? Give your answer as a proportional increase over the original amount he could borrow (##V_\text{before}##), so:
###\text{Proportional increase} = \frac{V_\text{after}-V_\text{before}}{V_\text{before}} ###Assume that:
- Interest rates are expected to be constant over the life of the loan.
- Loans are interest-only and have a life of 30 years.
- Mortgage loan payments are made every month in arrears and all interest rates are given as annualised percentage rates compounding per month.
The below screenshot of Commonwealth Bank of Australia's (CBA) details were taken from the Google Finance website on 7 Nov 2014. Some information has been deliberately blanked out.

What was CBA's approximate payout ratio over the 2014 financial year?
Note that the firm's interim and final dividends were $1.83 and $2.18 respectively over the 2014 financial year.
The below screenshot of Microsoft's (MSFT) details were taken from the Google Finance website on 28 Nov 2014. Some information has been deliberately blanked out.

What was MSFT's approximate payout ratio over the last year?
Note that MSFT's past four quarterly dividends were $0.31, $0.28, $0.28 and $0.28.
The following cash flows are expected:
- A perpetuity of yearly payments of $30, with the first payment in 5 years (first payment at t=5, which continues every year after that forever).
- One payment of $100 in 6 years and 3 months (t=6.25).
What is the NPV of the cash flows if the discount rate is 10% given as an effective annual rate?
Question 742 price gains and returns over time, no explanation
For an asset's price to quintuple (be five times as big, say from $1 to $5) every 5 years, what must be its effective annual capital return?
Bonds X and Y are issued by the same US company. Both bonds yield 6% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.
The only difference is that bond X pays coupons of 8% pa and bond Y pays coupons of 12% pa. Which of the following statements is true?
Question 574 inflation, real and nominal returns and cash flows, NPV
What is the present value of a nominal payment of $100 in 5 years? The real discount rate is 10% pa and the inflation rate is 3% pa.
Question 578 inflation, real and nominal returns and cash flows
Which of the following statements about inflation is NOT correct?
Question 604 inflation, real and nominal returns and cash flows
Apples and oranges currently cost $1 each. Inflation is 5% pa, and apples and oranges are equally affected by this inflation rate. Note that when payments are not specified as real, as in this question, they're conventionally assumed to be nominal.
Which of the following statements is NOT correct?
Question 664 real and nominal returns and cash flows, inflation, no explanation
What is the present value of real payments of $100 every year forever, with the first payment in one year? The nominal discount rate is 7% pa and the inflation rate is 4% pa.
Examine the graph of the AUD versus the USD, EUR and JPY. Note that RHS means right hand side and LHS left hand side which indicates which axis each line corresponds to. Assume inflation rates in each country were equal over the time period 1984 to 2018.
Which of the following statements is NOT correct?
Examine the below graph.
Which of the below statements is NOT correct?
Suppose the current Australian exchange rate is 0.8 USD per AUD.
If you think that the AUD will appreciate against the USD, contrary to the rest of the market, how could you profit? Right now you should:
Question 973 foreign exchange rate, monetary policy, no explanation
Suppose the market expects the Reserve Bank of Australia (RBA) to increase the policy rate by 25 basis points at their next meeting. The current exchange rate is 0.8 USD per AUD.
Then unexpectedly, the RBA announce that they will leave the policy rate unchanged due to increasing unemployment and fears of a potential recession.
What do you expect to happen to Australia's exchange rate on the day when the surprise announcement is made? The Australian dollar is likely to:
Question 974 foreign exchange rate, monetary policy, no explanation
Suppose the market expects the Bank of Japan (BoJ) to increase their short term interest rate by 15 basis points at their next meeting. The current short term interest rate is -0.1% pa and the exchange rate is 100 JPY per USD.
As expected, the BoJ announce that they will increase short term interest rate by 15 basis points.
What do you expect to happen to Japan’s exchange rate on the day when the announcement is made? The Japanese Yen (JPY) is likely to: