Fight Finance

Question 67  CFFA, interest tax shield

Here are the Net Income (NI) and Cash Flow From Assets (CFFA) equations:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###

###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###

What is the formula for calculating annual interest expense (IntExp) which is used in the equations above?

Select one of the following answers. Note that D is the value of debt which is constant through time, and ##r_D## is the cost of debt.

(a) ##D(1+r_D)##

(b) ##D/(1+r_D) ##

(c) ##D.r_D ##

(d) ##D / r_D##

(e) ##NI.r_D##

Question 89  WACC, CFFA, interest tax shield

A retail furniture company buys furniture wholesale and distributes it through its retail stores. The owner believes that she has some good ideas for making stylish new furniture. She is considering a project to buy a factory and employ workers to manufacture the new furniture she's designed. Furniture manufacturing has more systematic risk than furniture retailing.

Her furniture retailing firm's after-tax WACC is 20%. Furniture manufacturing firms have an after-tax WACC of 30%. Both firms are optimally geared. Assume a classical tax system.

Which method(s) will give the correct valuation of the new furniture-making project? Select the most correct answer.

(a) Discount the project's unlevered CFFA by the furniture manufacturing firms' 30% WACC after tax.

(b) Discount the project's unlevered CFFA by the company's 20% WACC after tax.

(c) Discount the project's levered CFFA by the company's 20% WACC after tax.

(d) Discount the project's levered CFFA by the furniture manufacturing firms' 30% WACC after tax.

(e) The methods outlined in answers (a) and (c) will give the same valuations, both are correct.

Question 113  WACC, CFFA, capital budgeting

The US firm Google operates in the online advertising business. In 2011 Google bought Motorola Mobility which manufactures mobile phones.

Assume the following:

• Google had a 10% after-tax weighted average cost of capital (WACC) before it bought Motorola.
• Motorola had a 20% after-tax WACC before it merged with Google.
• Google and Motorola have the same level of gearing.
• Both companies operate in a classical tax system.

You are a manager at Motorola. You must value a project for making mobile phones. Which method(s) will give the correct valuation of the mobile phone manufacturing project? Select the most correct answer.

The mobile phone manufacturing project's:

(a) Unlevered CFFA should be discounted by Google's 10% WACC after tax.

(b) Unlevered CFFA should be discounted by Motorola's 20% WACC after tax.

(c) Levered CFFA should be discounted by Google's 10% WACC after tax.

(d) Levered CFFA should be discounted by Motorola's 20% WACC after tax.

(e) Unlevered CFFA by 15%, the average of Google and Motorola's WACC after tax.

Question 69  interest tax shield, capital structure, leverage, WACC

Which statement about risk, required return and capital structure is the most correct?

(a) The before-tax cost of debt is less than the before-tax cost of equity. Therefore debt is a cheaper form of financing than equity so companies should try to finance their projects with debt only.

(b) Debt makes a firm's equity more risky. Therefore the higher the amount of debt, the higher the cost of equity.

(c) The more debt a firm has, the higher its tax shields. Therefore firms should seek to have as much debt and as little equity as possible.

(d) The more debt, the lower the firm's after tax WACC. The after tax WACC is the discount rate that discounts the firm's cash flows, so the lower it is the more the firm is worth. Therefore firms should try to make their after tax WACC as low as possible by using as much debt as possible.

(e) The less debt, the lower the chance of bankruptcy. Therefore firms should try to pay off all of their debt so that they are financed by equity only.

Question 74  WACC, capital structure, CAPM

A firm's weighted average cost of capital before tax (##r_\text{WACC before tax}##) would increase due to:

(a) The firm issuing more debt and using the proceeds to repurchase stock.

(b) The firm issuing more equity and using the proceeds to pay off debt holders.

(c) The firm's industry becoming more systematically risky, for example if it was a mining company whose performance became more sensitive to countries' GDP growth, so the correlation of the firm's returns with the market was higher.

(d) The firm's industry becoming less systematically risky, for example if it was a child care centre and the government announced higher subsidies for parents using child care centres, so the correlation of the firm's returns with the market was lower.

(e) None of the above.

Question 75  WACC, CAPM

A company has:

• 50 million shares outstanding.
• The market price of one share is currently $6.
• The risk-free rate is 5% and the market return is 10%.
• Market analysts believe that the company's ordinary shares have a beta of 2.
• The company has 1 million preferred stock which have a face (or par) value of $100 and pay a constant dividend of 10% of par. They currently trade for $80 each.
• The company's debentures are publicly traded and their market price is equal to 90% of their face value.
• The debentures have a total face value of $60,000,000 and the current yield to maturity of corporate debentures is 10% per annum. The corporate tax rate is 30%.

What is the company's after-tax weighted average cost of capital (WACC)? Assume a classical tax system.

(a) 11.75%

(b) 11.82%

(c) 13.54%

(d) 13.78%

(e) 20.84%

Question 78  WACC, capital structure

A company issues a large amount of bonds to raise money for new projects of similar risk to the company's existing projects. The net present value (NPV) of the new projects is positive but small. Assume a classical tax system. Which statement is NOT correct?

(a) The debt-to-assets (D/V) ratio will increase.

(b) The debt-to-equity ratio (D/E) will increase.

(c) Firm value is likely to have increased due to the higher amount of interest tax shields, assuming that there will not be any costs of financial distress.

(d) The company's after-tax WACC is likely to have decreased.

(e) The company's before-tax WACC is likely to have decreased.

Question 84  WACC, capital structure, capital budgeting

A firm is considering a new project of similar risk to the current risk of the firm. This project will expand its existing business. The cash flows of the project have been calculated assuming that there is no interest expense. In other words, the cash flows assume that the project is all-equity financed.

In fact the firm has a target debt-to-equity ratio of 1, so the project will be financed with 50% debt and 50% equity. To find the levered value of the firm's assets, what discount rate should be applied to the project's unlevered cash flows? Assume a classical tax system.

(a) The required return on equity, ##r_E##

(b) The required return on debt, ##r_D##

(c) The after-tax required return on debt, ##r_D.(1-t_c)##

(d) The after-tax WACC, ##\text{WACC after tax}=\frac{D}{V_L}.r_D.(1-t_c )+\frac{E_L}{V_L}.r_E##

(e) The pre-tax WACC, ##\text{WACC before tax}=\frac{D}{V_L}.r_D+\frac{E_L}{V_L}.r_E##

Question 88  WACC, CAPM

A firm can issue 3 year annual coupon bonds at a yield of 10% pa and a coupon rate of 8% pa.

The beta of its levered equity is 2. The market's expected return is 10% pa and 3 year government bonds yield 6% pa with a coupon rate of 4% pa.

The market value of equity is $1 million and the market value of debt is $1 million. The corporate tax rate is 30%.

What is the firm's after-tax WACC? Assume a classical tax system.

(a) 8.40%

(b) 10.50%

(c) 10.80%

(d) 12.00%

(e) 21.00%

Question 114  WACC, capital structure, risk

A firm's WACC before tax would decrease due to:

(a) the firm's industry becoming more systematically risky, for example if it was a mining company and commodities prices varied more strongly and were more positively correlated with the market portfolio.

(b) the firm's industry becoming less systematically risky, for example if it was a child care centre and the government announced permanently higher subsidies for parents' child care expenses.

(c) the firm issuing more debt and using the proceeds to repurchase stock.

(d) the firm issuing more equity and using the proceeds to pay off debt holders.

(e) none of the above.

Question 115  capital structure, leverage, WACC

A firm has a debt-to-assets ratio of 50%. The firm then issues a large amount of debt to raise money for new projects of similar market risk to the company's existing projects. Assume a classical tax system. Which statement is correct?

(a) The debt-to-assets (D/V) ratio will decrease.

(b) The debt-to-equity ratio (D/E) will decrease.

(c) The firm's cost of equity will decrease.

(d) The company's after-tax WACC will decrease.

(e) The company's before-tax WACC will decrease.

Question 302  WACC, CAPM

Which of the following statements about the weighted average cost of capital (WACC) is NOT correct?

(a) WACC before tax ##= r_D.\dfrac{D}{V_L} + r_{EL}.\dfrac{E_L}{V_L}##

(b) WACC before tax ##= r_f + \beta_{VL}.(r_m - r_f)##

(c) WACC after tax ##= r_D.(1-t_c).\dfrac{D}{V_L} + r_{EL}.\dfrac{E_L}{V_L}##

(d) WACC after tax ##= r_f + \beta_{VL}.(r_m - r_f) - \dfrac{r_D.D.t_c}{V_L}##

(e) WACC after tax ##= r_f + \beta_{VL}.(r_m - r_f)##

Question 303  WACC, CAPM, CFFA

There are many different ways to value a firm's assets. Which of the following will NOT give the correct market value of a levered firm's assets ##(V_L)##? Assume that:

• The firm is financed by listed common stock and vanilla annual fixed coupon bonds, which are both traded in a liquid market.
• The bonds' yield is equal to the coupon rate, so the bonds are issued at par. The yield curve is flat and yields are not expected to change. When bonds mature they will be rolled over by issuing the same number of new bonds with the same expected yield and coupon rate, and so on forever.
• Tax rates on the dividends and capital gains received by investors are equal, and capital gains tax is paid every year, even on unrealised gains regardless of when the asset is sold.
• There is no re-investment of the firm's cash back into the business. All of the firm's excess cash flow is paid out as dividends so real growth is zero.
• The firm operates in a mature industry with zero real growth.
• All cash flows and rates in the below equations are real (not nominal) and are expected to be stable forever. Therefore the perpetuity equation with no growth is suitable for valuation.

(a) ##V_L = n_\text{shares}.P_\text{share} + n_\text{bonds}.P_\text{bond}##

(b) ##V_L = n_\text{shares}.\dfrac{\text{Dividend per share}}{r_f + \beta_{EL}(r_m - r_f)} + n_\text{bonds}.\dfrac{\text{Coupon per bond}}{r_f + \beta_D(r_m - r_f)}##

(c) ##V_L = \dfrac{\text{CFFA}_{L}}{r_\text{WACC before tax}}##

(d) ##V_L = \dfrac{\text{CFFA}_{U}}{r_\text{WACC after tax}}##

(e) ##V_L = \dfrac{\text{CFFA}_{L}}{r_\text{WACC after tax}}##

Where:

###r_\text{WACC before tax} = r_D.\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital before tax}### ###r_\text{WACC after tax} = r_D.(1-t_c).\frac{D}{V_L} + r_{EL}.\frac{E_L}{V_L} = \text{Weighted average cost of capital after tax}### ###NI_L=(Rev-COGS-FC-Depr-\mathbf{IntExp}).(1-t_c) = \text{Net Income Levered}### ###CFFA_L=NI_L+Depr-CapEx - \varDelta NWC+\mathbf{IntExp} = \text{Cash Flow From Assets Levered}### ###NI_U=(Rev-COGS-FC-Depr).(1-t_c) = \text{Net Income Unlevered}### ###CFFA_U=NI_U+Depr-CapEx - \varDelta NWC= \text{Cash Flow From Assets Unlevered}###

Question 176  CFFA

Why is Capital Expenditure (CapEx) subtracted in the Cash Flow From Assets (CFFA) formula?

###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###

(a) CapEx is added in the Net Income (NI) equation so it needs subtracting in the CFFA equation.

(b) CapEx is a financing cash flow that needs to be ignored. Therefore it should be subtracted.

(c) CapEx is not a cash flow, it's a non-cash expense made up by accountants that needs to be subtracted.

(d) CapEx is subtracted to account for the net cash spent on capital assets.

(e) CapEx is subtracted because it's too hard to predict, therefore we exclude it.

Question 188  CFFA

Find Trademark Corporation's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Trademark Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	100
COGS	25
Operating expense	5
Depreciation	20
Interest expense	20
Income before tax	30
Tax at 30%	9
Net income	21

Trademark Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	120	80
PPE
Cost	150	140
Accumul. depr.	60	40
Carrying amount	90	100
Total assets	210	180
Liabilities
Current liabilities	75	65
Non-current liabilities	75	55
Owners' equity
Retained earnings	10	10
Contributed equity	50	50
Total L and OE	210	180

 

Note: all figures are given in millions of dollars ($m).

(a) -19

(b) 21

(c) 41

(d) 61

(e) 121

Question 206  CFFA, interest expense, interest tax shield

Interest expense (IntExp) is an important part of a company's income statement (or 'profit and loss' or 'statement of financial performance').

How does an accountant calculate the annual interest expense of a fixed-coupon bond that has a liquid secondary market? Select the most correct answer:

Annual interest expense is equal to:

(a) the bond's face value multiplied by its annual yield to maturity.

(b) the bond's face value multiplied by its annual coupon rate.

(c) the bond's market price at the start of the year multiplied by its annual yield to maturity.

(d) the bond's market price at the start of the year multiplied by its annual coupon rate.

(e) the future value of the actual cash payments of the bond over the year, grown to the end of the year, and grown by the bond's yield to maturity.

Question 208  CFFA

Find UniBar Corp's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

UniBar Corp
Income Statement for
year ending 30th June 2013
	$m
Sales	80
COGS	40
Operating expense	15
Depreciation	10
Interest expense	5
Income before tax	10
Tax at 30%	3
Net income	7

UniBar Corp
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	120	90
PPE
Cost	360	320
Accumul. depr.	40	30
Carrying amount	320	290
Total assets	440	380
Liabilities
Current liabilities	110	60
Non-current liabilities	190	180
Owners' equity
Retained earnings	95	95
Contributed equity	45	45
Total L and OE	440	380

 

Note: all figures are given in millions of dollars ($m).

(a) 12

(b) 2

(c) -8

(d) -18

(e) 48

Question 223  CFFA, interest tax shield

Which one of the following will increase the Cash Flow From Assets in this year for a tax-paying firm, all else remaining constant?

(a) An increase in net capital spending.

(b) A decrease in the cash flow to creditors.

(c) An increase in interest expense.

(d) An increase in net working capital.

(e) A decrease in dividends paid.

Question 224  CFFA

Cash Flow From Assets (CFFA) can be defined as:

(a) Cash available to distribute to creditors and stockholders.

(b) Cash flow to creditors minus cash flow to stockholders.

(c) Net income (or earnings) plus depreciation plus interest expense.

(d) Net income minus the increase in net working capital.

(e) Net income minus net capital spending minus the increase in net working capital.

Question 77  interest tax shield

The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###

###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###

For a firm with debt, what is the amount of the interest tax shield per year?

(a) ##IntExp.t_c##

(b) ##IntExp/t_c##

(c) ##IntExp.(1-t_c)##

(d) ##IntExp/(1-t_c)##

(e) ##IntExp.(t_c-1)##

Question 95  interest tax shield

The equations for Net Income (NI, also known as Earnings or Net Profit After Tax) and Cash Flow From Assets (CFFA, also known as Free Cash Flow to the Firm) per year are:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c)###

###CFFA=NI+Depr-CapEx - \varDelta NWC+IntExp###

For a firm with debt, what is the formula for the present value of interest tax shields if the tax shields occur in perpetuity?

You may assume:

• the value of debt (D) is constant through time,
• The cost of debt and the yield on debt are equal and given by ##r_D##.
• the appropriate rate to discount interest tax shields is ##r_D##.
• ##\text{IntExp}=D.r_D##

(a) ##D.t_c##

(b) ##D.r_D/t_c ##

(c) ##D.r_D.(1-t_c)##

(d) ##D.r_D/(1-t_c)##

(e) ##D.r_D.(t_c-1)##

Question 99  capital structure, interest tax shield, Miller and Modigliani, trade off theory of capital structure

A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged.

Assume that:

• The firm and individual investors can borrow at the same rate and have the same tax rates.
• The firm's debt and shares are fairly priced and the shares are repurchased at the market price, not at a premium.
• There are no market frictions relating to debt such as asymmetric information or transaction costs.
• Shareholders wealth is measured in terms of utiliity. Shareholders are wealth-maximising and risk-averse. They have a preferred level of overall leverage. Before the firm's capital restructure all shareholders were optimally levered.

According to Miller and Modigliani's theory, which statement is correct?

(a) The firm's share price and shareholder wealth will both decrease. This is because the firm will have more debt and therefore more risk so the discount rate applied to its cash flows will be higher, decreasing the value of the firm and therefore the value of the firm's equity and share price.

(b) The firm's share price and shareholder wealth will both increase. This is because the firm will have more debt which will amplify the returns of equity investors. This will mean that returns on equity can be much higher and investors will pay a premium for this, leading to an increase in the stock price.

(c) The firm's share price and shareholder wealth will both increase since it has more debt and therefore more tax shields.

(d) The firm's share price will increase due to the higher value of tax shields. But shareholder wealth will remain unchanged because capital structure is irrelevant when investors can use home-made leverage to create tax-shields themselves.

(e) The firm's share price and shareholder wealth will both increase. This is because the cost of debt is cheaper than equity, leading to a lower (before and after tax) WACC. This lower WACC will lead to a higher value of the firm and a higher share price.

Question 240  negative gearing, interest tax shield

Unrestricted negative gearing is allowed in Australia, New Zealand and Japan. Negative gearing laws allow income losses on investment properties to be deducted from a tax-payer's pre-tax personal income. Negatively geared investors benefit from this tax advantage. They also hope to benefit from capital gains which exceed the income losses.

For example, a property investor buys an apartment funded by an interest only mortgage loan. Interest expense is $2,000 per month. The rental payments received from the tenant living on the property are $1,500 per month. The investor can deduct this income loss of $500 per month from his pre-tax personal income. If his personal marginal tax rate is 46.5%, this saves $232.5 per month in personal income tax.

The advantage of negative gearing is an example of the benefits of:

(a) Diversification.

(b) The time value of money.

(c) Interest tax shields.

(d) Depreciation tax shields.

(e) A 'buy and hold' investment strategy.

Question 296  CFFA, interest tax shield

Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?

Remember:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###

(a) An increase in revenue (##Rev##).

(b) An decrease in revenue (##Rev##).

(c) An increase in rent expense (part of fixed costs, ##FC##).

(d) An increase in interest expense (##IntExp##).

(e) An increase in dividends.

Question 368  interest tax shield, CFFA

A method commonly seen in textbooks for calculating a levered firm's free cash flow (FFCF, or CFFA) is the following:

###\begin{aligned} FFCF &= (Rev - COGS - Depr - FC - IntExp)(1-t_c) + \\ &\space\space\space+ Depr - CapEx -\Delta NWC + IntExp(1-t_c) \\ \end{aligned}###

Does this annual FFCF or the annual interest tax shield?

Question 369  interest tax shield, CFFA

One formula for calculating a levered firm's free cash flow (FFCF, or CFFA) is to use earnings before interest and tax (EBIT).

###\begin{aligned} FFCF &= (EBIT)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ &= (Rev - COGS - Depr - FC)(1-t_c) + Depr - CapEx -\Delta NWC + IntExp.t_c \\ \end{aligned} \\###

Does this annual FFCF or the annual interest tax shield?

Question 94  leverage, capital structure, real estate

Your friend just bought a house for $400,000. He financed it using a $320,000 mortgage loan and a deposit of $80,000.

In the context of residential housing and mortgages, the 'equity' tied up in the value of a person's house is the value of the house less the value of the mortgage. So the initial equity your friend has in his house is $80,000. Let this amount be E, let the value of the mortgage be D and the value of the house be V. So ##V=D+E##.

If house prices suddenly fall by 10%, what would be your friend's percentage change in equity (E)? Assume that the value of the mortgage is unchanged and that no income (rent) was received from the house during the short time over which house prices fell.

Remember:

### r_{0\rightarrow1}=\frac{p_1-p_0+c_1}{p_0} ###

where ##r_{0-1}## is the return (percentage change) of an asset with price ##p_0## initially, ##p_1## one period later, and paying a cash flow of ##c_1## at time ##t=1##.

(a) -100%

(b) -50%

(c) -12.5%

(d) -10%

(e) -8%

Question 241  Miller and Modigliani, leverage, payout policy, diversification, NPV

One of Miller and Modigliani's (M&M's) important insights is that a firm's managers should not try to achieve a particular level of leverage in a world with zero taxes and perfect information since investors can make their own leverage. Therefore corporate capital structure policy is irrelevant since investors can achieve their own desired leverage at the personal level by borrowing or lending on their own.

This principal of 'home-made' or 'do-it-yourself' leverage can also be applied to other topics. Read the following statements to decide which are true:

(I) Payout policy: a firm's managers should not try to achieve a particular pattern of equity payout.

(II) Agency costs: a firm's managers should not try to minimise agency costs.

(III) Diversification: a firm's managers should not try to diversify across industries.

(IV) Shareholder wealth: a firm's managers should not try to maximise shareholders' wealth.

Which of the above statement(s) are true?

(a) I only.

(b) I and II only.

(c) I and III only.

(d) III only.

(e) All are true.

Question 301  leverage, capital structure, real estate

Your friend just bought a house for $1,000,000. He financed it using a $900,000 mortgage loan and a deposit of $100,000.

In the context of residential housing and mortgages, the 'equity' or 'net wealth' tied up in a house is the value of the house less the value of the mortgage loan. Assuming that your friend's only asset is his house, his net wealth is $100,000.

If house prices suddenly fall by 15%, what would be your friend's percentage change in net wealth?

Assume that:

• No income (rent) was received from the house during the short time over which house prices fell.
• Your friend will not declare bankruptcy, he will always pay off his debts.

(a) -1,000%

(b) -150%

(c) -100%

(d) -15%

(e) -10%

Question 104  CAPM, payout policy, capital structure, Miller and Modigliani, risk

Assume that there exists a perfect world with no transaction costs, no asymmetric information, no taxes, no agency costs, equal borrowing rates for corporations and individual investors, the ability to short the risk free asset, semi-strong form efficient markets, the CAPM holds, investors are rational and risk-averse and there are no other market frictions.

For a firm operating in this perfect world, which statement(s) are correct?

(i) When a firm changes its capital structure and/or payout policy, share holders' wealth is unaffected.

(ii) When the idiosyncratic risk of a firm's assets increases, share holders do not expect higher returns.

(iii) When the systematic risk of a firm's assets increases, share holders do not expect higher returns.

Select the most correct response:

(a) Only (i) is true.

(b) Only (ii) is true.

(c) Only (iii) is true.

(d) Only (i) and (ii) are true.

(e) All statements (i), (ii) and (iii) are true.

Question 98  capital structure, CAPM

A firm changes its capital structure by issuing a large amount of debt and using the funds to repurchase shares. Its assets are unchanged. Ignore interest tax shields.

According to the Capital Asset Pricing Model (CAPM), which statement is correct?

(a) The beta of the firm's assets will increase.

(b) The beta of the firm's assets will decrease.

(c) The beta of the firm's equity will increase.

(d) The beta of the firm's equity will decrease.

(e) The beta of the firm's equity will be unchanged.

Question 3  DDM, income and capital returns

The following equation is called the Dividend Discount Model (DDM), Gordon Growth Model or the perpetuity with growth formula: ### P_0 = \frac{ C_1 }{ r - g } ###

What is ##g##? The value ##g## is the long term expected:

(a) Income return of the stock.

(b) Capital return of the stock.

(c) Total return of the stock.

(d) Dividend yield of the stock.

(e) Price-earnings ratio of the stock.

Question 5  DDM

For a price of $6, Carlos will sell you a share which will pay a dividend of $1 in one year and every year after that forever. The required return of the stock is 10% pa.

Would you like to his share or politely ?

Question 7  DDM

For a price of $1040, Camille will sell you a share which just paid a dividend of $100, and is expected to pay dividends every year forever, growing at a rate of 5% pa.

So the next dividend will be ##100(1+0.05)^1=$105.00##, and the year after it will be ##100(1+0.05)^2=110.25## and so on.

The required return of the stock is 15% pa.

Would you like to the share or politely ?

Question 8  DDM

For a price of $10.20 each, Renee will sell you 100 shares. Each share is expected to pay dividends in perpetuity, growing at a rate of 5% pa. The next dividend is one year away (t=1) and is expected to be $1 per share.

The required return of the stock is 15% pa.

Would you like to the shares or politely ?

Question 9  DDM, NPV

For a price of $129, Joanne will sell you a share which is expected to pay a $30 dividend in one year, and a $10 dividend every year after that forever. So the stock's dividends will be $30 at t=1, $10 at t=2, $10 at t=3, and $10 forever onwards.

The required return of the stock is 10% pa.

Would you like to the share or politely ?

Question 10  DDM

For a price of $95, Sherylanne will sell you a share which is expected to pay its first dividend of $10 in 7 years (t=7), and will continue to pay the same $10 dividend every year after that forever.

The required return of the stock is 10% pa.

Would you like to the share or politely ?

Question 18  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

### p_{0} = \frac{c_1}{r_{\text{eff}} - g_{\text{eff}}} ###

What is the discount rate '## r_\text{eff} ##' in this equation?

(a) The expected total return of the stock.

(b) The expected capital return of the stock.

(c) The expected dividend return of the stock.

(d) The expected income return of the stock.

(e) The expected growth rate of the stock price.

Question 28  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

### P_{0} = \frac{C_1}{r_{\text{eff}} - g_{\text{eff}}} ###

What would you call the expression ## C_1/P_0 ##?

(a) The expected total return of the stock.

(b) The expected income return of the stock.

(c) The expected capital return of the stock.

(d) The expected growth rate of the dividend.

(e) The expected growth rate of the stock price.

Question 31  DDM, perpetuity with growth, effective rate conversion

What is the NPV of the following series of cash flows when the discount rate is 5% given as an effective annual rate?

The first payment of $10 is in 4 years, followed by payments every 6 months forever after that which shrink by 2% every 6 months. That is, the growth rate every 6 months is actually negative 2%, given as an effective 6 month rate. So the payment at ## t=4.5 ## years will be ## 10(1-0.02)^1=9.80 ##, and so on.

(a) $188.62

(b) $184.07

(c) $120.43

(d) $117.53

(e) $8.07

Question 36  DDM, perpetuity with growth

A stock pays annual dividends which are expected to continue forever. It just paid a dividend of $10. The growth rate in the dividend is 2% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?

(a) $127.5

(b) $125

(c) $102

(d) $101.98

(e) $100

Question 41  DDM, income and capital returns

The following is the Dividend Discount Model (DDM) used to price stocks:

### P_0 = \frac{d_1}{r-g} ###

Assume that the assumptions of the DDM hold and that the time period is measured in years.

Which of the following is equal to the expected dividend in 3 years, ## d_3 ##?

(a) ## d_1(1+g)^3 ##

(b) ## P_3(r-g) ##

(c) ## d_2(1+g)^2 ##

(d) ## P_0(1+g)^3(r-g) ##

(e) ## P_0(1+g)^2(r-g) ##

Question 54  NPV, DDM

A stock is expected to pay the following dividends:

Cash Flows of a Stock
Time (yrs)	0	1	2	3	4	...
Dividend ($)	0.00	1.15	1.10	1.05	1.00	...

After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,

• the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
• the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.

The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.

What is the current price of the stock?

(a) $7.2968

(b) $7.5018

(c) $7.6667

(d) $7.7522

(e) $9.4101

Question 55  NPV, DDM

A stock is expected to pay the following dividends:

Cash Flows of a Stock
Time (yrs)	0	1	2	3	4	...
Dividend ($)	0.00	1.15	1.10	1.05	1.00	...

After year 4, the annual dividend will grow in perpetuity at -5% pa. Note that this is a negative growth rate, so the dividend will actually shrink. So,

• the dividend at t=5 will be ##$1(1-0.05) = $0.95##,
• the dividend at t=6 will be ##$1(1-0.05)^2 = $0.9025##, and so on.

The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates.

What will be the price of the stock in four and a half years (t = 4.5)?

(a) $5.2615

(b) $6.0386

(c) $6.3333

(d) $6.6425

(e) $11.9040

Question 142  DDM, income and capital returns

When using the dividend discount model to price a stock:

### p_{0} = \frac{d_1}{r - g} ###

The growth rate of dividends (g):

(a) Is the stock's required return.

(b) Is the stock's expected total return.

(c) Is the stock's expected dividend return.

(d) Is the stock's expected real yield.

(e) Should be less than the expected GDP growth rate of the country where the company does business.

Question 148  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

### p_0 = \frac{d_1}{r - g} ###

Which expression is NOT equal to the expected dividend yield?

(a) ## r-g ##

(b) ## \dfrac{d_1}{p_0} ##

(c) ## \dfrac{d_5}{p_4} ##

(d) ## \dfrac{d_5(1+g)^2}{p_6} ##

(e) ## \dfrac{d_3}{p_0(1+r)^2} ##

Question 150  DDM, effective rate

A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock is 10% pa, given as an effective annual rate.

What is the price of the share now?

(a) $127.50

(b) $171.14

(c) $173.33

(d) $174.56

(e) $354.06

Question 158  DDM, income and capital returns

The following equation is the Dividend Discount Model, also known as the 'Gordon Growth Model' or the 'Perpetuity with growth' equation.

###p_0=\frac{d_1}{r_\text{eff}-g_\text{eff}}###

Which expression is NOT equal to the expected capital return?

(a) ## g_\text{eff} ##

(b) ## \dfrac{p_1}{p_0} -1 ##

(c) ## \dfrac{d_5}{d_4} -1 ##

(d) ## \dfrac{d_1}{p_0} - 1 ##

(e) ## \dfrac{p_1-p_0}{p_0} ##

Question 161  DDM

A share just paid its semi-annual dividend of $10. The dividend is expected to grow at 2% every 6 months forever. This 2% growth rate is an effective 6 month rate. Therefore the next dividend will be $10.20 in six months. The required return of the stock 10% pa, given as an effective annual rate.

What is the price of the share now?

(a) $127.50

(b) $171.14

(c) $173.33

(d) $174.56

(e) $354.06

Question 165  DDM, PE ratio, payout ratio

For certain shares, the forward-looking Price-Earnings Ratio (##P_0/EPS_1##) is equal to the inverse of the share's total expected return (##1/r_\text{total}##). For what shares is this true?

Use the general accounting definition of 'payout ratio' which is dividends per share (DPS) divided by earnings per share (EPS) and assume that all cash flows, earnings and rates are real rather than nominal.

A company's forward-looking PE ratio will be the inverse of its total expected return on equity when it has a:

(a) 100% payout ratio and high expected growth in earnings and dividends.

(b) 100% payout ratio and negative expected growth in earnings and dividends.

(c) 100% payout ratio and no expected growth in earnings or dividends.

(d) 0% payout ratio and no expected growth in earnings or dividends.

(e) 0% payout ratio and negative expected growth in earnings and dividends.

Question 166  DDM, no explanation

A stock pays annual dividends. It just paid a dividend of $3. The growth rate in the dividend is 4% pa. You estimate that the stock's required return is 10% pa. Both the discount rate and growth rate are given as effective annual rates. Using the dividend discount model, what will be the share price?

(a) 30

(b) 31.16

(c) 31.2

(d) 50

(e) 52

Question 169  NPV, DDM

A stock is expected to pay the following dividends:

Cash Flows of a Stock
Time (yrs)	0	1	2	3	4	...
Dividend ($)	8	8	8	20	8	...

After year 4, the dividend will grow in perpetuity at 4% pa. The required return on the stock is 10% pa. Both the growth rate and required return are given as effective annual rates. Note that the $8 dividend at time zero is about to be paid tonight.

What is the current price of the stock?

(a) 170.24

(b) 141.09

(c) 137.09

(d) 131.62

(e) 127.98

Question 171  DDM, income and capital returns

The following is the Dividend Discount Model used to price stocks:

### p_0=\frac{d_1}{r-g} ###

Which of the following statements about the Dividend Discount Model is NOT correct?

(a) The dividend yield is equal to ##(r-g)##.

(b) The dividend yield is equal to ##\left( \dfrac{d_1}{p_0} \right)##.

(c) The total return of the stock is equal to ##(r)##.

(d) The total return of the stock is equal to ##\left( \dfrac{d_1+p_0.g}{p_0} \right)##.

(e) The total return of the stock is equal to ##(r+g)##.

Question 181  DDM

A stock pays annual dividends. It just paid a dividend of $5. The growth rate in the dividend is 1% pa. You estimate that the stock's required return is 8% pa. Both the discount rate and growth rate are given as effective annual rates.

Using the dividend discount model, what will be the share price?

(a) 72.1429

(b) 71.4286

(c) 63.1250

(d) 63.1150

(e) 62.5000

Question 232  CAPM, DDM

A stock has a beta of 0.5. Its next dividend is expected to be $3, paid one year from now. Dividends are expected to be paid annually and grow by 2% pa forever. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. All returns are effective annual rates.

What is the price of the stock now?

(a) $55.6364

(b) $54.5455

(c) $40.8

(d) $40

(e) $37.5

Question 248  CAPM, DDM, income and capital returns

The total return of any asset can be broken down in different ways. One possible way is to use the dividend discount model (or Gordon growth model):

###p_0 = \frac{c_1}{r_\text{total}-r_\text{capital}}###

Which, since ##c_1/p_0## is the income return (##r_\text{income}##), can be expressed as:

###r_\text{total}=r_\text{income}+r_\text{capital}###

So the total return of an asset is the income component plus the capital or price growth component.

Another way to break up total return is to use the Capital Asset Pricing Model:

###r_\text{total}=r_\text{f}+β(r_\text{m}- r_\text{f})###

###r_\text{total}=r_\text{time value}+r_\text{risk premium}###

So the risk free rate is the time value of money and the term ##β(r_\text{m}- r_\text{f})## is the compensation for taking on systematic risk.

Using the above theory and your general knowledge, which of the below equations, if any, are correct?

(I) ##r_\text{income}=r_\text{time value}##

(II) ##r_\text{income}=r_\text{risk premium}##

(III) ##r_\text{capital}=r_\text{time value}##

(IV) ##r_\text{capital}=r_\text{risk premium}##

(V) ##r_\text{income}+r_\text{capital}=r_\text{time value}+r_\text{risk premium}##

Which of the equations are correct?

(a) I, IV and V only.

(b) II, III and V only.

(c) V only.

(d) All are true.

(e) None are true.

Question 289  DDM, expected and historical returns, ROE

In the dividend discount model:

###P_0 = \dfrac{C_1}{r-g}###

The return ##r## is supposed to be the:

(a) Expected future total return of the market price of equity.

(b) Expected future total return of the book price of equity.

(c) Actual historical total return on the market price of equity.

(d) Actual historical total return on the book price of equity.

(e) Actual historical return on equity (ROE) defined as (Net Income / Owners Equity).

Question 329  DDM, expected and historical returns

In the dividend discount model:

### P_0= \frac{d_1}{r-g} ###

The pronumeral ##g## is supposed to be the:

(a) Expected future growth rate of the dividend.

(b) Actual historical growth rate of the dividend.

(c) Expected future growth rate of the total required return on equity r.

(d) Actual historical growth rate of the market share price.

(e) Actual historical growth rate of the return on equity (ROE) defined as (Net Income / Owners Equity).

Question 333  DDM, time calculation

When using the dividend discount model, care must be taken to avoid using a nominal dividend growth rate that exceeds the country's nominal GDP growth rate. Otherwise the firm is forecast to take over the country since it grows faster than the average business forever.

Suppose a firm's nominal dividend grows at 10% pa forever, and nominal GDP growth is 5% pa forever. The firm's total dividends are currently $1 billion (t=0). The country's GDP is currently $1,000 billion (t=0).

In approximately how many years will the company's total dividends be as large as the country's GDP?

(a) 1,443 years

(b) 1,199 years

(c) 955 years

(d) 674 years

(e) 148 years

Question 362  income and capital returns, DDM, real estate

Three years ago Frederika bought a house for $400,000.

Now it's worth $600,000, based on recent similar sales in the area.

Frederika's residential property has an expected total return of 7% pa.

She rents her house out for $2,500 per month, paid in advance. Every 12 months she plans to increase the rental payments.

The present value of 12 months of rental payments is $29,089.48.

The future value of 12 months of rental payments one year ahead is $31,125.74.

What is the expected annual capital yield of the property?

(a) -0.7814%

(b) -0.2724%

(c) 1.8124%

(d) 2%

(e) 2.1518%

Question 21  income and capital returns, bond pricing

A fixed coupon bond was bought for $90 and paid its annual coupon of $3 one year later (at t=1 year). Just after the coupon was paid, the bond price was $92 (at t=1 year). What was the total return, capital return and income return? Calculate your answers as effective annual rates.

The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.

(a) -0.0556, -0.0222, -0.0333

(b) 0.0222, -0.0111, 0.0333.

(c) 0.0333, 0.0556, 0.0222.

(d) 0.0556, 0.0222, 0.0333.

(e) 0.0556, 0.0333, 0.0222.

Question 30  income and capital returns

A share was bought for $20 (at t=0) and paid its annual dividend of $3 one year later (at t=1). Just after the dividend was paid, the share price was $16 (at t=1). What was the total return, capital return and income return? Calculate your answers as effective annual rates.

The choices are given in the same order: ## r_\text{total},r_\text{capital},r_\text{income} ##.

(a) -0.2, -0.35, 0.15.

(b) -0.05, -0.2, 0.15.

(c) -0.05, 0.15, -0.2.

(d) 0.05, 0.2, -0.15.

(e) 0.15, -0.05, -0.2.

Question 136  income and capital returns

A stock was bought for $8 and paid a dividend of $0.50 one year later (at t=1 year). Just after the dividend was paid, the stock price was $7 (at t=1 year).

What were the total, capital and dividend returns given as effective annual rates? The choices are given in the same order:

##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.

(a) 0.0625, -0.0625, -0.125.

(b) 0.0625, 0.125, -0.0625.

(c) -0.0625, 0.0625, -0.125.

(d) -0.0625, -0.125, 0.0625.

(e) -0.125, -0.1875, 0.0625.

Question 151  income and capital returns

A share was bought for $30 (at t=0) and paid its annual dividend of $6 one year later (at t=1).

Just after the dividend was paid, the share price fell to $27 (at t=1). What were the total, capital and income returns given as effective annual rates?

The choices are given in the same order:

##r_\text{total}## , ##r_\text{capital}## , ##r_\text{dividend}##.

(a) -0.1, -0.3, 0.2.

(b) -0.1, 0.1, -0.2.

(c) 0.1, -0.1, 0.2.

(d) 0.1, 0.2, -0.1.

(e) 0.2, 0.1, -0.1.

Question 162  income and capital returns

A share was bought for $10 (at t=0) and paid its annual dividend of $0.50 one year later (at t=1). Just after the dividend was paid, the share price was $11 (at t=1).

What was the total return, capital return and income return? Calculate your answers as effective annual rates. The choices are given in the same order:

##r_\text{total}##, ##r_\text{capital}##, ##r_\text{dividend}##.

(a) -0.15, -0.1, -0.05.

(b) 0.05, 0.15, 0.1.

(c) 0.1, 0.05, 0.05.

(d) 0.15, 0.05, 0.1.

(e) 0.15, 0.1, 0.05.

Question 210  real estate, inflation, real and nominal returns and cash flows, income and capital returns

Assume that the Gordon Growth Model (same as the dividend discount model or perpetuity with growth formula) is an appropriate method to value real estate.

An old rule of thumb in the real estate industry is that properties should yield a 5% pa rental return. Some investors also regard property to be as risky as the stock market, therefore property is thought to have a required total return of 9% pa which is the average total return on the stock market including dividends.

Assume that all returns are effective annual rates and they are nominal (not reduced by inflation). Inflation is expected to be 2% pa.

You're considering purchasing an investment property which has a rental yield of 5% pa and you expect it to have the same risk as the stock market. Select the most correct statement about this property.

(a) The nominal property price is expected to grow by approximately 9% pa.

(b) The nominal property price is expected to grow by approximately 5% pa.

(c) The nominal property price is expected to grow by approximately 4% pa.

(d) The real property price is expected to grow by approximately 7% pa.

(e) The real property price is expected to grow by approximately 6% pa.

Question 282  expected and historical returns, income and capital returns

You're the boss of an investment bank's equities research team. Your five analysts are each trying to find the expected total return over the next year of shares in a mining company. The mining firm:

• Is regarded as a mature company since it's quite stable in size and was floated around 30 years ago. It is not a high-growth company;
• Share price is very sensitive to changes in the price of the market portfolio, economic growth, the exchange rate and commodities prices. Due to this, its standard deviation of total returns is much higher than that of the market index;
• Experienced tough times in the last 10 years due to unexpected falls in commodity prices.
• Shares are traded in an active liquid market.

Your team of analysts present their findings, and everyone has different views. While there's no definitive true answer, whose calculation of the expected total return is the most plausible? Assume that:

• The analysts' source data is correct and true, but their inferences might be wrong;
• All returns and yields are given as effective annual nominal rates.

(a) Alice says 5% pa since she calculated that this was the average total yield on government bonds over the last 10 years. She says that this is also the expected total yield implied by current prices on one year government bonds.

(b) Bob says 4% pa since he calculated that this was the average total return on the mining stock over the last 10 years.

(c) Cate says 3% pa since she calculated that this was the average growth rate of the share price over the last 10 years.

(d) Dave says 6% pa since he calculated that this was the average growth rate of the share market price index (not the accumulation index) over the last 10 years.

(e) Eve says 15% pa since she calculated that this was the discount rate implied by the dividend discount model using the current share price, forecast dividend in one year and a 3% growth rate in dividends thereafter, which is the expected long term inflation rate.

Question 341  Multiples valuation, PE ratio

Estimate Microsoft's (MSFT) share price using a price earnings (PE) multiples approach with the following assumptions and figures only:

• Apple, Google and Microsoft are comparable companies,
• Apple's (AAPL) share price is $526.24 and historical EPS is $40.32.
• Google's (GOOG) share price is $1,215.65 and historical EPS is $36.23.
• Micrsoft's (MSFT) historical earnings per share (EPS) is $2.71.

Source: Google Finance 28 Feb 2014.

(a) $63.15

(b) $61.67

(c) $30.83

(d) $28.25

(e) $8.60

Question 347  PE ratio, Multiples valuation

Which of the following investable assets are NOT suitable for valuation using PE multiples techniques?

(a) Common equity in small private companies.

(b) Common equity in large private companies.

(c) Common equity in listed public companies.

(d) Fixed term bonds of listed public companies.

(e) Real estate.

Question 348  PE ratio, Multiples valuation

Estimate the US bank JP Morgan's share price using a price earnings (PE) multiples approach with the following assumptions and figures only:

• The major US banks JP Morgan Chase (JPM), Citi Group (C) and Wells Fargo (WFC) are comparable companies;
• JP Morgan Chase's historical earnings per share (EPS) is $4.37;
• Citi Group's share price is $50.05 and historical EPS is $4.26;
• Wells Fargo's share price is $48.98 and historical EPS is $3.89.

Note: Figures sourced from Google Finance on 24 March 2014.

(a) $53.2353

(b) $53.1831

(c) $53.0995

(d) $26.5498

(e) $2.7849

Question 354  PE ratio, Multiples valuation

Which firms tend to have low forward-looking price-earnings (PE) ratios?

Only consider firms with positive earnings, disregard firms with negative earnings and therefore negative PE ratios.

(a) Illiquid small private companies.

(b) High growth technology firms.

(c) Firms expected to have temporarily low earnings over the next year, but with higher earnings later.

(d) Firms with a very low level of systematic risk.

(e) Firms whose assets include a very large proportion of cash.

Question 209  CFFA

Find Piano Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

Piano Bar
Income Statement for
year ending 30th June 2013
	$m
Sales	310
COGS	185
Operating expense	20
Depreciation	15
Interest expense	10
Income before tax	80
Tax at 30%	24
Net income	56

Piano Bar
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	240	230
PPE
Cost	420	400
Accumul. depr.	50	35
Carrying amount	370	365
Total assets	610	595
Liabilities
Current liabilities	180	190
Non-current liabilities	290	265
Owners' equity
Retained earnings	90	90
Contributed equity	50	50
Total L and OE	610	595

 

Note: all figures are given in millions of dollars ($m).

(a) 116

(b) 61

(c) 56

(d) 41

(e) 11

Question 226  CFFA

Find World Bar's Cash Flow From Assets (CFFA), also known as Free Cash Flow to the Firm (FCFF), over the year ending 30th June 2013.

World Bar
Income Statement for
year ending 30th June 2013
	$m
Sales	300
COGS	150
Operating expense	50
Depreciation	40
Interest expense	10
Taxable income	50
Tax at 30%	15
Net income	35

World Bar
Balance Sheet
as at 30th June	2013	2012
	$m	$m
Assets
Current assets	200	230
PPE
Cost	400	400
Accumul. depr.	75	35
Carrying amount	325	365
Total assets	525	595
Liabilities
Current liabilities	150	205
Non-current liabilities	235	250
Owners' equity
Retained earnings	100	100
Contributed equity	40	40
Total L and OE	525	595

 

Note: all figures above and below are given in millions of dollars ($m).

(a) 145

(b) 100

(c) 90

(d) 60

(e) -20

Question 273  CFFA, capital budgeting

Value the following business project to manufacture a new product.

Project Data
Project life	2 yrs
Initial investment in equipment	$6m
Depreciation of equipment per year	$3m
Expected sale price of equipment at end of project	$0.6m
Unit sales per year	4m
Sale price per unit	$8
Variable cost per unit	$5
Fixed costs per year, paid at the end of each year	$1m
Interest expense per year	0
Tax rate	30%
Weighted average cost of capital after tax per annum	10%

Notes

1. The firm's current assets and current liabilities are $3m and $2m respectively right now. This net working capital will not be used in this project, it will be used in other unrelated projects.
   Due to the project, current assets (mostly inventory) will grow by $2m initially (at t = 0), and then by $0.2m at the end of the first year (t=1).
   Current liabilities (mostly trade creditors) will increase by $0.1m at the end of the first year (t=1).
   At the end of the project, the net working capital accumulated due to the project can be sold for the same price that it was bought.
2. The project cost $0.5m to research which was incurred one year ago.

Assumptions

• All cash flows occur at the start or end of the year as appropriate, not in the middle or throughout the year.
• All rates and cash flows are real. The inflation rate is 3% pa.
• All rates are given as effective annual rates.
• The business considering the project is run as a 'sole tradership' (run by an individual without a company) and is therefore eligible for a 50% capital gains tax discount when the equipment is sold, as permitted by the Australian Tax Office.

What is the expected net present value (NPV) of the project?

(a) $5.2m

(b) $8.481735m

(c) $8.743802m

(d) $8.991736m

(e) $9.719008m

Question 342  CFFA, capital budgeting

A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.

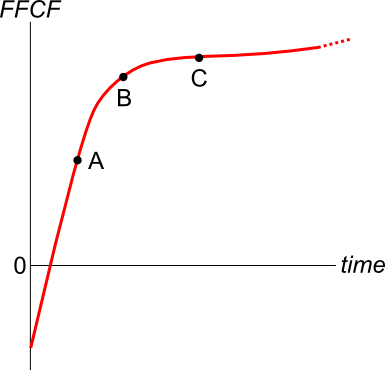
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:

###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###

Which point corresponds to the best time to calculate the terminal value?

(a) Point A.

(b) Point B.

(c) Point C.

(d) Any of the points.

(e) None of the points.

Question 343  CFFA, capital budgeting

An old company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.

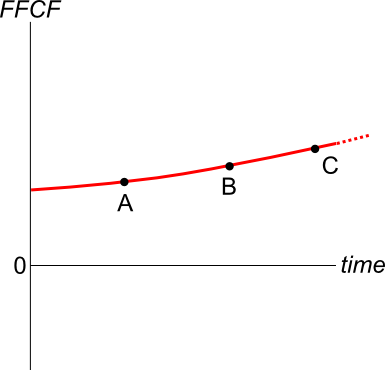
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:

###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###

Which point corresponds to the best time to calculate the terminal value?

(a) Point A.

(b) Point B.

(c) Point C.

(d) Any of the points.

(e) None of the points.

Question 344  CFFA, capital budgeting

A new company's Firm Free Cash Flow (FFCF, same as CFFA) is forecast in the graph below.

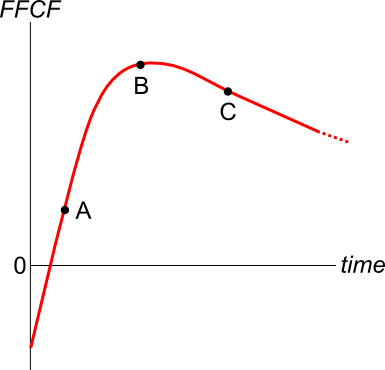
To value the firm's assets, the terminal value needs to be calculated using the perpetuity with growth formula:

###V_{\text{terminal, }t-1} = \dfrac{FFCF_{\text{terminal, }t}}{r-g}###

Which point corresponds to the best time to calculate the terminal value?

(a) Point A.

(b) Point B.

(c) Point C.

(d) Any of the points.

(e) None of the points.

Question 349  CFFA, depreciation tax shield

Which one of the following will decrease net income (NI) but increase cash flow from assets (CFFA) in this year for a tax-paying firm, all else remaining constant?

Remember:

###NI = (Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - \Delta NWC+IntExp###

(a) An increase in revenue (Rev).

(b) An increase in rent expense (part of fixed costs, FC).

(c) An increase in depreciation expense (Depr).

(d) An decrease in net working capital (ΔNWC).

(e) An increase in dividends.

Question 351  CFFA

Over the next year, the management of an unlevered company plans to:

• Achieve firm free cash flow (FFCF or CFFA) of $1m.
• Pay dividends of $1.8m
• Complete a $1.3m share buy-back.
• Spend $0.8m on new buildings without buying or selling any other fixed assets. This capital expenditure is included in the CFFA figure quoted above.

Assume that:

• All amounts are received and paid at the end of the year so you can ignore the time value of money.
• The firm has sufficient retained profits to pay the dividend and complete the buy back.
• The firm plans to run a very tight ship, with no excess cash above operating requirements currently or over the next year.

How much new equity financing will the company need? In other words, what is the value of new shares that will need to be issued?

(a) $2.1m

(b) $1.3m

(c) $0.8m

(d) $0.3m

(e) No new shares need to be issued, the firm will be sufficiently financed.

Question 359  CFFA

Which one of the following will have no effect on net income (NI) but decrease cash flow from assets (CFFA or FFCF) in this year for a tax-paying firm, all else remaining constant?

Remember:

###NI=(Rev-COGS-FC-Depr-IntExp).(1-t_c )### ###CFFA=NI+Depr-CapEx - ΔNWC+IntExp###

(a) An increase in revenue (Rev).

(b) An increase in rent expense (a type of recurring fixed cost, FC).

(c) An increase in depreciation expense (Depr).

(d) An increase in inventories (a current asset).

(e) An decrease in interest expense (IntExp).

Question 366  opportunity cost, NPV, CFFA

Your friend is trying to find the net present value of an investment which:

• Costs $1 million initially (t=0); and
• Pays a single positive cash flow of $1.1 million in one year (t=1).

The investment has a total required return of 10% pa due to its moderate level of undiversifiable risk.

Your friend is aware of the importance of opportunity costs and the time value of money, but he is unsure of how to find the NPV of the project.

He knows that the opportunity cost of investing the $1m in the project is the expected gain from investing the money in shares instead. Like the project, shares also have an expected return of 10% since they have moderate undiversifiable risk. This opportunity cost is $0.1m ##(=1m \times 10\%)## which occurs in one year (t=1).

He knows that the time value of money should be accounted for, and this can be done by finding the present value of the cash flows in one year.

Your friend has listed a few different ways to find the NPV which are written down below.

Method 1: ##-1m + \dfrac{1.1m}{(1+0.1)^1} ##

Method 2: ##-1m + 1.1m - 1m \times 0.1 ##

Method 3: ##-1m + \dfrac{1.1m}{(1+0.1)^1} - 1m \times 0.1 ##

Which of the above calculations give the correct NPV? Select the most correct answer.

(a) Method 1 only.

(b) Method 2 only.

(c) Method 3 only.

(d) Methods 1 and 2 only.

(e) Methods 1 and 3 only.

Question 93  correlation, CAPM, systematic risk

A stock's correlation with the market portfolio increases while its total risk is unchanged. What will happen to the stock's expected return and systematic risk?

(a) The stock will have a higher return and higher systematic risk.

(b) The stock will have a lower return and higher systematic risk.

(c) The stock will have a higher return and lower systematic risk.

(d) The stock will have a lower return and lower systematic risk.

(e) The stock's return and systematic risk will be unchanged.

Question 111  portfolio risk, correlation

All things remaining equal, the variance of a portfolio of two positively-weighted stocks rises as:

(a) The correlation between the stocks' returns rise.

(b) The correlation between the stocks' returns decline.

(c) The portfolio standard deviation declines.

(d) Both stocks' individual variances decline.

(e) Both stocks' individual standard deviations decline.

Question 236  diversification, correlation, risk

Diversification in a portfolio of two assets works best when the correlation between their returns is:

(a) -1

(b) -0.5

(c) 0

(d) 0.5

(e) 1

Question 293  covariance, correlation, portfolio risk

All things remaining equal, the higher the correlation of returns between two stocks:

(a) The more diversification is possible when those stocks are combined in a portfolio.

(b) The lower the variance of returns of an equally-weighted portfolio of those stocks.

(c) The lower the volatility of returns of an equal-weighted portfolio of those stocks.

(d) The higher the covariance between those stocks' returns.

(e) The more likely that when one stock has a positive return, the other has a negative return.

Question 285  covariance, portfolio risk

Two risky stocks A and B comprise an equal-weighted portfolio. The correlation between the stocks' returns is 70%.

If the variance of stock A's returns increases but the:

• Prices and expected returns of each stock stays the same,
• Variance of stock B's returns stays the same,
• Correlation of returns between the stocks stays the same.

Which of the following statements is NOT correct?

(a) The variance of the portfolio returns will increase.

(b) The standard deviation of the portfolio returns will increase.

(c) The covariance of returns between stocks A and B will stay the same.

(d) The portfolio expected return will stay the same.

(e) The portfolio value will stay the same.

Question 66  CAPM, SML

Government bonds currently have a return of 5% pa. A stock has an expected return of 6% pa and the market return is 7% pa. What is the beta of the stock?

(a) -0.5

(b) 0

(c) 0.5

(d) 1

(e) 7

Question 71  CAPM, risk

Stock A has a beta of 0.5 and stock B has a beta of 1. Which statement is NOT correct?

(a) Stock A has less systematic risk than stock B, so stock A is expected to return less than stock B.

(b) Stock B has the same systematic risk as the market, so they're expected to have the same return.

(c) Stock B has the same beta as the market, so it also has the same total risk as the market.

(d) If stock A and B were combined in a portfolio with weights of 50% each, the beta of the portfolio would be 0.75.

(e) Stocks A and B have more systematic risk than the risk free security (government bonds) so their return should be greater than the risk free rate.

Question 72  CAPM, portfolio beta, portfolio risk

Portfolio Details
Stock	Expected return	Standard deviation	Correlation	Beta	Dollars invested
A	0.2	0.4	0.12	0.5	40
B	0.3	0.8		1.5	80

What is the beta of the above portfolio?

(a) 0.75

(b) 0.833333333

(c) 1

(d) 1.166666667

(e) 1.4

Question 76  CAPM, SML

Government bonds currently have a return of 5%. A stock has a beta of 2 and the market return is 7%. What is the expected return of the stock?

(a) 5%

(b) 7%

(c) 9%

(d) 12%

(e) 19%

Question 79  CAPM, risk

Which statement is the most correct?

(a) The risk free rate has zero systematic risk and zero idiosyncratic risk.

(b) The market portfolio has zero idiosyncratic risk.

(c) The market portfolio has zero systematic risk.

(d) a and b are true.

(e) a and c are true.

Question 80  CAPM, risk, diversification

Diversification is achieved by investing in a large amount of stocks. What type of risk is reduced by diversification?

(a) Idiosyncratic risk.

(b) Systematic risk.

(c) Both idiosyncratic and systematic risk.

(d) Market risk.

(e) Beta risk.

Question 86  CAPM

Treasury bonds currently have a return of 5% pa. A stock has a beta of 0.5 and the market return is 10% pa. What is the expected return of the stock?

(a) 5% pa

(b) 7.5% pa

(c) 10% pa

(d) 12.5% pa

(e) 20% pa

Question 90  CAPM, risk

According to the theory of the Capital Asset Pricing Model (CAPM), total variance can be broken into two components, systematic variance and idiosyncratic variance. Which of the following events would be considered the most diversifiable according to the theory of the CAPM?

(a) Global economic recession.

(b) A major terrorist attack, grounding all commercial aircraft in the US and Europe.

(c) An increase in corporate tax rates.

(d) The outbreak of world war.

(e) A company's poor earnings announcement.

Question 92  CAPM, SML, CML

Which statement(s) are correct?

(i) All stocks that plot on the Security Market Line (SML) are fairly priced.

(ii) All stocks that plot above the Security Market Line (SML) are overpriced.

(iii) All fairly priced stocks that plot on the Capital Market Line (CML) have zero idiosyncratic risk.

Select the most correct response:

(a) Only (i) is true.

(b) Only (ii) is true.

(c) Only (iii) is true.

(d) All statements (i), (ii) and (iii) are true.

(e) Only statements (i) and (iii) are true.

Question 106  CAPM

A fairly priced stock has an expected return of 15% pa. Treasury bonds yield 5% pa and the market portfolio's expected return is 10% pa. What is the beta of the stock?

(a) 0

(b) 0.5

(c) 1

(d) 1.5

(e) 2

Question 110  CAPM, SML, NPV

The security market line (SML) shows the relationship between beta and expected return.

Buying investment projects that plot above the SML would lead to:

(a) A positive NPV.

(b) A zero NPV.

(c) A negative NPV.

(d) A large amount of diversifiable risk.

(e) Zero diversifiable risk.

Question 112  CAPM, risk

According to the theory of the Capital Asset Pricing Model (CAPM), total risk can be broken into two components, systematic risk and idiosyncratic risk. Which of the following events would be considered a systematic, undiversifiable event according to the theory of the CAPM?

(a) A decrease in house prices in one city.

(b) An increase in mining industry tax rates.

(c) An increase in corporate tax rates.

(d) A case of fraud at a major retailer.

(e) A poor earnings announcement from a major firm.

Question 235  SML, NPV, CAPM, risk

The security market line (SML) shows the relationship between beta and expected return.

Investment projects that plot on the SML would have:

(a) A positive NPV and should be accepted.

(b) A zero NPV.

(c) A negative NPV and should be rejected.

(d) A large amount of diversifiable risk.

(e) Zero diversifiable risk.

Question 244  CAPM, SML, NPV, risk

Examine the following graph which shows stocks' betas ##(\beta)## and expected returns ##(\mu)##:

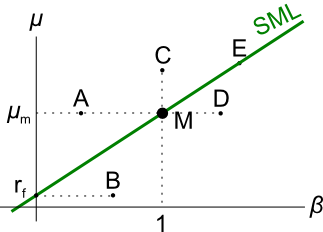
Assume that the CAPM holds and that future expectations of stocks' returns and betas are correctly measured. Which statement is NOT correct?

(a) Asset A is underpriced.

(b) Asset B has a negative alpha (a negative excess return or abnormal return).

(c) Buying asset C would be a positive NPV investment.

(d) Asset D has less systematic variance than the market portfolio (M).

(e) Asset E is fairly priced.

Question 100  market efficiency, technical analysis, joint hypothesis problem

A company selling charting and technical analysis software claims that independent academic studies have shown that its software makes significantly positive abnormal returns. Assuming the claim is true, which statement(s) are correct?

(I) Weak form market efficiency is broken.

(II) Semi-strong form market efficiency is broken.

(III) Strong form market efficiency is broken.

(IV) The asset pricing model used to measure the abnormal returns (such as the CAPM) had mis-specification error so the returns may not be abnormal but rather fair for the level of risk.

Select the most correct response:

(a) Only III is true.

(b) Only II and III are true.

(c) Only I, II and III are true.

(d) Only IV is true.

(e) Either I, II and III are true, or IV is true, or they are all true.

Question 105  NPV, risk, market efficiency

A person is thinking about borrowing $100 from the bank at 7% pa and investing it in shares with an expected return of 10% pa. One year later the person intends to sell the shares and pay back the loan in full. Both the loan and the shares are fairly priced.

What is the Net Present Value (NPV) of this one year investment? Note that you are asked to find the present value (##V_0##), not the value in one year (##V_1##).

(a) $10

(b) $3

(c) $2.8037

(d) $2.7273

(e) $0

Question 119  market efficiency, fundamental analysis, joint hypothesis problem

Your friend claims that by reading 'The Economist' magazine's economic news articles, she can identify shares that will have positive abnormal expected returns over the next 2 years. Assuming that her claim is true, which statement(s) are correct?

(i) Weak form market efficiency is broken.

(ii) Semi-strong form market efficiency is broken.

(iii) Strong form market efficiency is broken.

(iv) The asset pricing model used to measure the abnormal returns (such as the CAPM) is either wrong (mis-specification error) or is measured using the wrong inputs (data errors) so the returns may not be abnormal but rather fair for the level of risk.

Select the most correct response:

(a) Only (iii) is true.

(b) Only (ii) and (iii) are true.

(c) Only (i), (ii) and (iii) are true.

(d) Either (ii) and (iii) are true, or (iv) is true, or (ii), (iii) and (iv) are true.

(e) Either (i), (ii) and (iii) are true, or (iv) is true, or all are true.

Question 242  technical analysis, market efficiency

Select the most correct statement from the following.

'Chartists', also known as 'technical traders', believe that:

(a) Markets are weak-form efficient.

(b) Markets are semi-strong-form efficient.

(c) Past prices cannot be used to predict future prices.

(d) Past returns can be used to predict future returns.

(e) Stock prices reflect all publically available information.

Question 243  fundamental analysis, market efficiency

Fundamentalists who analyse company financial reports and news announcements (but who don't have inside information) will make positive abnormal returns if:

(a) Markets are weak and semi-strong form efficient but strong-form inefficient.

(b) Markets are weak form efficient but semi-strong and strong-form inefficient.

(c) Chartists make negative excess returns.

(d) Insiders make positive excess returns.

(e) Insiders make negative excess returns.

Question 338  market efficiency, CAPM, opportunity cost, technical analysis

A man inherits $500,000 worth of shares.

He believes that by learning the secrets of trading, keeping up with the financial news and doing complex trend analysis with charts that he can quit his job and become a self-employed day trader in the equities markets.

What is the expected gain from doing this over the first year? Measure the net gain in wealth received at the end of this first year due to the decision to become a day trader. Assume the following:

• He earns $60,000 pa in his current job, paid in a lump sum at the end of each year.
• He enjoys examining share price graphs and day trading just as much as he enjoys his current job.
• Stock markets are weak form and semi-strong form efficient.
• He has no inside information.
• He makes 1 trade every day and there are 250 trading days in the year. Trading costs are $20 per trade. His broker invoices him for the trading costs at the end of the year.
• The shares that he currently owns and the shares that he intends to trade have the same level of systematic risk as the market portfolio.
• The market portfolio's expected return is 10% pa.

Measure the net gain over the first year as an expected wealth increase at the end of the year.

(a) $110,000

(b) $50,000

(c) $45,000

(d) -$15,000

(e) -$65,000

Question 340  market efficiency, opportunity cost

A managed fund charges fees based on the amount of money that you keep with them. The fee is 2% of the start-of-year amount, but it is paid at the end of every year.

This fee is charged regardless of whether the fund makes gains or losses on your money.

The fund offers to invest your money in shares which have an expected return of 10% pa before fees.

You are thinking of investing $100,000 in the fund and keeping it there for 40 years when you plan to retire.

What is the Net Present Value (NPV) of investing your money in the fund? Note that the question is not asking how much money you will have in 40 years, it is asking: what is the NPV of investing in the fund? Assume that:

• The fund has no private information.
• Markets are weak and semi-strong form efficient.
• The fund's transaction costs are negligible.
• The cost and trouble of investing your money in shares by yourself, without the managed fund, is negligible.

(a) $0

(b) -$20,000.00

(c) -$48,000.17

(d) -$51,999.83

(e) -$80,000.00

Question 128  debt terminology, needs refinement

An 'interest payment' is the same thing as a 'coupon payment'. or ?

Question 129  debt terminology

An 'interest rate' is the same thing as a 'coupon rate'. or ?

Question 130  debt terminology

An 'interest rate' is the same thing as a 'yield'. or ?

Question 330  APR, effective rate, debt terminology

Which of the following statements about effective rates and annualised percentage rates (APR's) is NOT correct?

(a) Effective rates compound once over their time period. So an effective monthly rate compounds once per month.

(b) APR's compound more than once per year. So an APR compounding monthly compounds 12 times per year. The exception is an APR that compounds annually (once per year) which is the same thing as an effective annual rate.

(c) To convert an effective rate to an APR, multiply the effective rate by the number of time periods in one year. So an effective monthly rate multiplied by 12 is equal to an APR compounding monthly.

(d) To convert an APR compounding monthly to an effective monthly rate, divide the APR by the number of months in one year (12).

(e) To convert an APR compounding monthly to an effective weekly rate, divide the APR by the number of weeks in one year (approximately 52).

Question 372  debt terminology

Which of the following statements is NOT correct? Borrowers:

(a) Receive cash at the start and promise to pay cash in the future, as set out in the debt contract.

(b) Are debtors.

(c) Owe money.

(d) Are funded by debt.

(e) Buy debt.

Question 373  debt terminology

Which of the following statements is NOT correct? Lenders:

(a) Are long debt.

(b) Invest in debt.

(c) Are owed money.

(d) Provide debt funding.

(e) Have debt liabilities.

Question 374  debt terminology

Which of the following statements is NOT equivalent to the yield on debt?

Assume that the debt being referred to is fairly priced, but do not assume that it's priced at par.

(a) Debt coupon rate.

(b) Required return on debt.

(c) Total return on debt.

(d) Opportunity cost of debt.

(e) Cost of debt capital.

Question 109  credit rating, credit risk

Bonds with lower (worse) credit ratings tend to have:

(a) Lower yields to maturity.

(b) Higher probabilities of default.

(c) Lower coupon rates when priced at par.

(d) Lower total risk.

(e) Lower credit risk.

Question 120  credit risk, payout policy

A newly floated farming company is financed with senior bonds, junior bonds, cumulative non-voting preferred stock and common stock. The new company has no retained profits and due to floods it was unable to record any revenues this year, leading to a loss. The firm is not bankrupt yet since it still has substantial contributed equity (same as paid-up capital).

On which securities must it pay interest or dividend payments in this terrible financial year?

(a) Preferred stock only.

(b) The senior and junior bonds only.

(c) Common stock only.

(d) The senior and junior bonds and the preferred stock.

(e) No payments on any security is required since the firm made a loss.

Question 197  credit risk, bank accepted bill

A highly levered risky firm is trying to raise more debt. The types of debt being considered, in no particular order, are senior bonds, junior bonds, bank accepted bills, promissory notes and bank loans.

Which of these forms of debt is the safest from the perspective of the debt investors who are thinking of investing in the firm's new debt?

(a) Senior bonds

(b) Junior bonds

(c) Bank accepted bills

(d) Promissory notes

(e) Bank loans

Question 221  credit risk

You're considering making an investment in a particular company. They have preference shares, ordinary shares, senior debt and junior debt.

Which is the safest investment? Which has the highest expected returns?

(a) Junior debt is the safest. Preference shares have the highest expected returns.

(b) Preference shares are the safest. Ordinary shares have the highest expected returns.

(c) Senior debt is the safest. Ordinary shares have the highest expected returns.

(d) Junior debt is the safest. Ordinary shares have the highest expected returns.

(e) Senior debt is the safest. Junior debt have the highest expected returns.

Question 24  implicit interest rate in wholesale credit, effective rate

A bathroom and plumbing supplies shop offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.

What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given in this question are effective annual rates.

(a) 0.0004

(b) 0.1299

(c) 0.1308

(d) 0.1377

(e) 0.1493

Question 34  implicit interest rate in wholesale credit

A wholesale glass importer offers credit to its customers. Customers are given 30 days to pay for their goods, but if they pay within 5 days they will get a 1% discount.

What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 5th day or the 30th day. All rates given below are effective annual rates.

(a) 0.1580

(b) 0.1460

(c) 0.1365

(d) 0.1301

(e) 0.0004

Question 62  implicit interest rate in wholesale credit

A wholesale building supplies business offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay within 7 days they will get a 2% discount.

What is the effective interest rate implicit in the discount being offered?

Assume 365 days in a year and that all customers pay on either the 7th day or the 60th day. All rates given below are effective annual rates.

(a) 0.000381

(b) 0.129887

(c) 0.137736

(d) 0.149276

(e) 0.278643

Question 139  implicit interest rate in wholesale credit

A wholesale shop offers credit to its customers. The customers are given 21 days to pay for their goods. But if they pay straight away (now) they get a 1% discount.

What is the effective interest rate given to customers who pay in 21 days? All rates given below are effective annual rates. Assume 365 days in a year.

(a) 0.0005

(b) 0.0006

(c) 0.1603

(d) 0.1738

(e) 0.1909

Question 154  implicit interest rate in wholesale credit, no explanation

A wholesale vitamin supplements store offers credit to its customers. Customers are given 30 days to pay for their goods, but if they pay within 5 days they will get a 1% discount.

What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay on either the 5th day or the 30th day. All of the below answer choices are given as effective annual interest rates.

(a) 0.158047

(b) 0.146000

(c) 0.136477

(d) 0.063047

(e) 0.000402

Question 164  implicit interest rate in wholesale credit

A wholesale store offers credit to its customers. Customers are given 60 days to pay for their goods, but if they pay immediately they will get a 1.5% discount.

What is the effective interest rate implicit in the discount being offered? Assume 365 days in a year and that all customers pay either immediately or the 60th day. All of the below answer choices are given as effective annual interest rates.

(a) 0.0003

(b) 0.0878

(c) 0.0913

(d) 0.0948

(e) 0.0963

Question 297  implicit interest rate in wholesale credit

You just bought $100,000 worth of inventory from a wholesale supplier. You are given the option of paying within 5 days and receiving a 2% discount, or paying the full price within 60 days.

You actually don't have the cash to pay within 5 days, but you could borrow it from the bank (as an overdraft) at 10% pa, given as an effective annual rate.

In 60 days you will have enough money to pay the full cost without having to borrow from the bank.

What is the implicit interest rate charged by the wholesale supplier, given as an effective annual rate? Also, should you borrow from the bank in 5 days to pay the supplier and receive the discount? Or just pay the full price on the last possible date?

Assume that there are 365 days per year.

(a) 0.143476 is the implicit rate. The buying firm should borrow from the bank and pay at day 5.

(b) 0.130771 is the implicit rate. The buying firm should NOT borrow from the bank and just pay at day 60.

(c) 0.125473 is the implicit rate. The buying firm should borrow from the bank and pay at day 5.

(d) 0.120131 is the implicit rate. The buying firm should NOT borrow from the bank and just pay at day 60.

(e) 0.020408 is the implicit rate. The buying firm should borrow from the bank and pay at day 5.

Question 58  NPV, inflation, real and nominal returns and cash flows, Annuity

A project to build a toll bridge will take two years to complete, costing three payments of $100 million at the start of each year for the next three years, that is at t=0, 1 and 2.

After completion, the toll bridge will yield a constant $50 million at the end of each year for the next 10 years. So the first payment will be at t=3 and the last at t=12. After the last payment at t=12, the bridge will be given to the government.

The required return of the project is 21% pa given as an effective annual nominal rate.

All cash flows are real and the expected inflation rate is 10% pa given as an effective annual rate. Ignore taxes.

The Net Present Value is:

(a) -$112,496,484

(b) -$32,260,693

(c) -$19,645,987

(d) $5,222,533

(e) $200,000,000

Question 353  income and capital returns, inflation, real and nominal returns and cash flows, real estate

A residential investment property has an expected nominal total return of 6% pa and nominal capital return of 3% pa.

Inflation is expected to be 2% pa. All rates are given as effective annual rates.

What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.

(a) 3.9216%, 2.9412%, 0.9804%.

(b) 3.9216%, 0.9804%, 2.9412%.

(c) 3.9216%, 0.9804%, 0.9804%.

(d) 1.9804%, 1.0000%, 0.9804%.

(e) 1.9608%, 0.9804%, 0.9804%.

Question 363  income and capital returns, inflation, real and nominal returns and cash flows, real estate

A residential investment property has an expected nominal total return of 8% pa and nominal capital return of 3% pa.

Inflation is expected to be 2% pa. All rates are given as effective annual rates.

What are the property's expected real total, capital and income returns? The answer choices below are given in the same order.

(a) 5.8824%, 0.9804%, 4.902%.

(b) 5.8824%, 0.9804%, 2.9412%.

(c) 4.0000%, 1.0000%, 3.0000%.

(d) 3.9412%, 1.0000%, 2.9412%.

(e) 3.9216%, 0.9804%, 2.9412%.

Question 16  credit card, APR, effective rate

A credit card offers an interest rate of 18% pa, compounding monthly.

Find the effective monthly rate, effective annual rate and the effective daily rate. Assume that there are 365 days in a year.

All answers are given in the same order:

### r_\text{eff monthly} , r_\text{eff yearly} , r_\text{eff daily} ###

(a) 0.0072, 0.09, 0.0002.

(b) 0.0139, 0.18, 0.0005.

(c) 0.0139, 6.2876, 0.0055.

(d) 0.015, 0.1956, 0.0005.

(e) 0.015, 0.1956, 0.006.

Question 26  APR, effective rate

A European bond paying annual coupons of 6% offers a yield of 10% pa.

Convert the yield into an effective monthly rate, an effective annual rate and an effective daily rate. Assume that there are 365 days in a year.

All answers are given in the same order:

### r_\text{eff, monthly} , r_\text{eff, yearly} , r_\text{eff, daily} ###

(a) 0.0041, 0.05, 0.0001.

(b) 0.0080, 0.1, 0.0003.

(c) 0.0083, 0.1, 0.0003.

(d) 0.0083, 2.1384, 0.0031.

(e) 0.0083, 0.1047, 0.0033.

Question 131  APR, effective rate

Calculate the effective annual rates of the following three APR's:

• A credit card offering an interest rate of 18% pa, compounding monthly.
• A bond offering a yield of 6% pa, compounding semi-annually.
• An annual dividend-paying stock offering a return of 10% pa compounding annually.

All answers are given in the same order:

##r_\text{credit card, eff yrly}##, ##r_\text{bond, eff yrly}##, ##r_\text{stock, eff yrly}##

(a) 0.1956, 0.0609, 0.1.

(b) 0.015, 0.09, 0.1.

(c) 0.1881, 0.0609, 0.1025.

(d) 0.1956, 0.0617, 0.1047.

(e) 6.2876, 0.1236, 0.1.

Question 134  fully amortising loan, APR

You want to buy an apartment worth $400,000. You have saved a deposit of $80,000. The bank has agreed to lend you the $320,000 as a fully amortising mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?

(a) $888.89

(b) $1,600.00

(c) $1,885.99

(d) $1,918.56

(e) $23,247.65

Question 146  APR, effective rate

A three year corporate bond yields 12% pa with a coupon rate of 10% pa, paid semi-annually.

Find the effective six month yield, effective annual yield and the effective daily yield. Assume that each month has 30 days and that there are 360 days in a year.

All answers are given in the same order:

##r_\text{eff semi-annual}##, ##r_\text{eff yearly}##, ##r_\text{eff daily}##.

(a) 0.06, 0.1236, 0.000324.

(b) 0.058301, 0.12, 0.000315.

(c) 0.05, 0.1025, 0.000271.

(d) 0.05, 0.1, 0.000278.

(e) 0.048809, 0.1, 0.000265.

Question 149  fully amortising loan, APR

You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as a fully amortising loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?

(a) $32,692.01

(b) $2,697.98

(c) $2,652.17

(d) $2,250.00

(e) $1,250.00

Question 156  APR, effective rate

A 2 year government bond yields 5% pa with a coupon rate of 6% pa, paid semi-annually.

Find the effective six month rate, effective annual rate and the effective daily rate. Assume that each month has 30 days and that there are 360 days in a year.

All answers are given in the same order:

##r_\text{eff semi-annual}##, ##r_\text{eff yrly}##, ##r_\text{eff daily}##.

(a) 0.024695, 0.05, 0.000136.

(b) 0.025, 0.050625, 0.000137.

(c) 0.029563, 0.06, 0.000162.

(d) 0.03, 0.06, 0.000167.

(e) 0.03, 0.0609, 0.000164.

Question 172  fully amortising loan, APR

You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $2,000 per month. The interest rate is 9% pa which is not expected to change.

How much did you borrow? After 5 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.

(a) 246,567.70,   93,351.63

(b) 246,567.70,   235,741.91

(c) 248,563.73,   96,346.75

(d) 248,563.73,   238,323.24

(e) 256,580.38,   245,314.97

Question 187  fully amortising loan, APR

You just signed up for a 30 year fully amortising mortgage with monthly payments of $1,000 per month. The interest rate is 6% pa which is not expected to change.

How much did you borrow? After 20 years, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change.

(a) 169,672.58,     90,724.32

(b) 166,791.61,     90,073.45

(c) 166,791.61,     139,580.77

(d) 165,177.97,     88,321.04

(e) 165,177.97,     137,639.05

Question 203  fully amortising loan, APR

You just signed up for a 30 year fully amortising mortgage loan with monthly payments of $1,500 per month. The interest rate is 9% pa which is not expected to change.

How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change.

(a) 184,925.77,     164,313.82

(b) 184,925.77,     115,517.84

(c) 186,422.80,     166,717.43

(d) 186,422.80,     118,412.54

(e) 192,435.28,     170,986.32

Question 222  fully amortising loan, APR

You just agreed to a 30 year fully amortising mortgage loan with monthly payments of $2,500. The interest rate is 9% pa which is not expected to change.

How much did you borrow? After 10 years, how much will be owing on the mortgage? The interest rate is still 9% and is not expected to change. The below choices are given in the same order.

(a) $320,725.47,     $284,977.19

(b) $310,704.66,     $277,862.39

(c) $310,704.66,     $197,354.23

(d) $308,209.62,     $273,856.37

(e) $308,209.62,     $192,529.73

Question 256  APR, effective rate

A 2 year corporate bond yields 3% pa with a coupon rate of 5% pa, paid semi-annually.

Find the effective monthly rate, effective six month rate, and effective annual rate.

##r_\text{eff monthly}##, ##r_\text{eff 6 month}##, ##r_\text{eff annual}##.

(a) 0.002466, 0.014889, 0.03.

(b) 0.002485, 0.015, 0.030225.

(c) 0.004074, 0.024695, 0.05.

(d) 0.004124, 0.025, 0.050625.

(e) 0.004167, 0.025, 0.05.

Question 259  fully amortising loan, APR

You want to buy a house priced at $400,000. You have saved a deposit of $40,000. The bank has agreed to lend you $360,000 as a fully amortising loan with a term of 30 years. The interest rate is 8% pa payable monthly and is not expected to change.

What will be your monthly payments?

(a) $1,000

(b) $1,106.6497

(c) $2,400

(d) $2,571.8327

(e) $2,641.5525

Question 12  bond pricing

For a price of $100, Carol will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with similar risk, maturity and coupon characteristics trade at a yield of 12% pa.

Would you like to her bond or politely ?

Question 13  bond pricing

For a price of $100, Rad will sell you a 5 year bond paying semi-annual coupons of 16% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.

Would you like to the bond or politely ?

Question 14  bond pricing

For a price of $100, Andrea will sell you a 2 year bond paying annual coupons of 10% pa. The face value of the bond is $100. Other bonds with the same risk, maturity and coupon characteristics trade at a yield of 6% pa.

Would you like to the bond or politely ?

Question 17  bond pricing

A three year bond has a face value of $100, a yield of 10% and a fixed coupon rate of 5%, paid semi-annually. What is its price?

(a) 87.31

(b) 86.92

(c) 76.37

(d) 74.62

(e) 58.63

Question 23  bond pricing, premium par and discount bonds

Bonds X and Y are issued by the same US company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond X and Y's coupon rates are 8 and 12% pa respectively. Which of the following statements is true?

(a) Bonds X and Y are premium bonds.

(b) Bonds X and Y are discount bonds.

(c) Bond X is a discount bond but bond Y is a premium bond.

(d) Bond X is a premium bond but bond Y is a discount bond.

(e) Bonds X and Y are par bonds.

Question 25  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

A European company just issued two bonds, a

• 2 year zero coupon bond at a yield of 8% pa, and a
• 3 year zero coupon bond at a yield of 10% pa.

What is the company's forward rate over the third year (from t=2 to t=3)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.

(a) 0.0374

(b) 0.0604

(c) 0.1204

(d) 0.1250

(e) 0.1411

Question 33  bond pricing, premium par and discount bonds

Bonds A and B are issued by the same company. They have the same face value, maturity, seniority and coupon payment frequency. The only difference is that bond A has a 5% coupon rate, while bond B has a 10% coupon rate. The yield curve is flat, which means that yields are expected to stay the same.

Which bond would have the higher current price?

(a) Bond A will have a higher price.

(b) Bond B will have a higher price.

(c) Bonds A and B will have the same price.

(d) The higher priced bond can't be determined without knowing their yields.

(e) The higher priced bond can't be determined without knowing the inflation rate.

Question 35  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

A European company just issued two bonds, a

• 1 year zero coupon bond at a yield of 8% pa, and a
• 2 year zero coupon bond at a yield of 10% pa.

What is the company's forward rate over the second year (from t=1 to t=2)? Give your answer as an effective annual rate, which is how the above bond yields are quoted.

(a) 0.0185

(b) 0.0374

(c) 0.0604

(d) 0.1204

(e) 0.1250

Question 38  bond pricing

A two year Government bond has a face value of $100, a yield of 0.5% and a fixed coupon rate of 0.5%, paid semi-annually. What is its price?

(a) $100.0000

(b) $98.0346

(c) $99.0062

(d) $99.0087

(e) $99.0124

Question 48  IRR, NPV, bond pricing, premium par and discount bonds, market efficiency

The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.

Considering this, which of the following statements is NOT correct?

(a) The internal rate of return (IRR) of buying a fairly priced bond is equal to the bond's yield.

(b) The Present Value of a fairly priced bond's coupons and face value is equal to its price.

(c) If a fairly priced bond's required return rises, its price will fall.

(d) Fairly priced premium bonds' yields are less than their coupon rates, prices are more than their face values, and the NPV of buying them is therefore positive.

(e) The NPV of buying a fairly priced bond is zero.

Question 63  bond pricing, NPV, market efficiency

The theory of fixed interest bond pricing is an application of the theory of Net Present Value (NPV). Also, a 'fairly priced' asset is not over- or under-priced. Buying or selling a fairly priced asset has an NPV of zero.

Considering this, which of the following statements is NOT correct?

(a) The internal rate of return (IRR) of buying a bond is equal to the bond's yield.

(b) The present value of a fairly priced bond's coupons and face value is equal to its price.

(c) If the required return of a bond falls, its price will fall.

(d) Fairly priced discount bonds' yield is more than the coupon rate, price is less than face value, and the NPV of buying them is zero.

(e) The NPV of buying a fairly priced bond is zero.

Question 96  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

An Australian company just issued two bonds paying semi-annual coupons:

• 1 year zero coupon bond at a yield of 8% pa, and a
• 2 year zero coupon bond at a yield of 10% pa.

What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

(a) 6.01%

(b) 6.02%

(c) 9.20%

(d) 12.02%

(e) 18.40%

Question 108  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

An Australian company just issued two bonds:

• A 1 year zero coupon bond at a yield of 10% pa, and
• A 2 year zero coupon bond at a yield of 8% pa.

What is the forward rate on the company's debt from years 1 to 2? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

(a) 0.1840

(b) 0.1202

(c) 0.0920

(d) 0.0602

(e) 0.0301

Question 133  bond pricing

A bond maturing in 10 years has a coupon rate of 4% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value of the bond is $100. What is its price?

(a) $33.93

(b) $55.37

(c) $57.61

(d) $68.28

(e) $85.12

Question 143  bond pricing, zero coupon bond, term structure of interest rates, forward interest rate

An Australian company just issued two bonds:

• A 6-month zero coupon bond at a yield of 6% pa, and
• A 12 month zero coupon bond at a yield of 7% pa.

What is the company's forward rate from 6 to 12 months? Give your answer as an APR compounding every 6 months, which is how the above bond yields are quoted.

(a) 0.0400

(b) 0.0500

(c) 0.0660

(d) 0.0800

(e) 0.1321

Question 159  bond pricing

A three year bond has a fixed coupon rate of 12% pa, paid semi-annually. The bond's yield is currently 6% pa. The face value is $100. What is its price?

(a) $116.25

(b) $74.04

(c) $85.89

(d) $83.75

(e) $71.38

Question 163  bond pricing, premium par and discount bonds

Bonds X and Y are issued by different companies, but they both pay a semi-annual coupon of 10% pa and they have the same face value ($100), maturity (3 years) and yield (10%) as each other.

Which of the following statements is true?

(a) Bonds X and Y are premium bonds.

(b) Bonds X and Y are discount bonds.

(c) Bond X is a discount bond but bond Y is a premium bond.

(d) Bond X is a premium bond but bond Y is a discount bond.

(e) Bonds X and Y are par bonds.

Question 168  bond pricing

A four year bond has a face value of $100, a yield of 6% and a fixed coupon rate of 12%, paid semi-annually. What is its price?

(a) 67.2123

(b) 78.9409

(c) 81.7042

(d) 111.1513

(e) 121.0591

Question 178  bond pricing, premium par and discount bonds

Which one of the following bonds is trading at a discount?

(a) a ten-year bond with a $4000 face value whose yield to maturity is 6.0% and coupon rate is 6.5% paid semi-annually.

(b) a 6-year bond with a principal of $40,000 and a price of $45,000.

(c) a 15-year bond with a $10,000 face value whose yield to maturity is 8.0% and coupon rate is 10.0% paid semi-annually.

(d) a two-year bond with a $50,000 face value whose yield to maturity is 5.2% and coupon rate is 5.2% paid semi-annually.

(e) None of the above bonds are discount bonds.

Question 179  bond pricing, capital raising

A firm wishes to raise $20 million now. They will issue 8% pa semi-annual coupon bonds that will mature in 5 years and have a face value of $100 each. Bond yields are 6% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

(a) 140,202

(b) 184,280

(c) 184,460

(d) 186,881

(e) 200,000

Question 183  bond pricing

A five year bond has a face value of $100, a yield of 12% and a fixed coupon rate of 6%, paid semi-annually.

What is the bond's price?

(a) 36.2655

(b) 55.8395

(c) 59.3381

(d) 77.9197

(e) 87.3629

Question 193  bond pricing, premium par and discount bonds

Which one of the following bonds is trading at par?

(a) a ten-year bond with a $4000 face value whose yield to maturity is 6.0% and coupon rate is 6.5% paid semi-annually.

(b) a 6-year bond with a principal of $40,000 and a price of $45,000.

(c) a 15-year bond with a $10,000 face value whose yield to maturity is 8.0% and coupon rate is 10.0% paid semi-annually.

(d) a two-year bond with a $50,000 face value whose yield to maturity is 5.2% compounding semi-annually which has a price of $50,000.

(e) None of the above bonds are trading at par.

Question 194  bond pricing, capital raising

A firm wishes to raise $8 million now. They will issue 7% pa semi-annual coupon bonds that will mature in 10 years and have a face value of $100 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue?

(a) 107,441

(b) 98,393

(c) 90,480

(d) 80,000

(e) 64,039

Question 227  bond pricing, premium par and discount bonds

Which one of the following bonds is trading at a premium?

(a) a ten-year bond with a $4,000 face value whose yield to maturity is 6.0% and coupon rate is 5.9% paid semi-annually.

(b) a fifteen-year bond with a $10,000 face value whose yield to maturity is 8.0% and coupon rate is 7.8% paid semi-annually.

(c) a five-year bond with a $2,000 face value whose yield to maturity is 7.0% and coupon rate is 7.2% paid semi-annually.

(d) a two-year bond with a $50,000 face value whose yield to maturity is 5.2% and coupon rate is 5.2% paid semi-annually.

(e) None of the above bonds are premium bonds.

Question 229  bond pricing

An investor bought two fixed-coupon bonds issued by the same company, a zero-coupon bond and a 7% pa semi-annual coupon bond. Both bonds have a face value of $1,000, mature in 10 years, and had a yield at the time of purchase of 8% pa.

A few years later, yields fell to 6% pa. Which of the following statements is correct? Note that a capital gain is an increase in price.

(a) The zero-coupon bond and the 7% semi-annual coupon bond were both discount bonds but now they are both premium bonds.

(b) The zero-coupon bond and the 7% semi-annual coupon bond were both premium bonds but now they are both discount bonds.

(c) When yields fell, the investor made a capital loss on both bonds.

(d) When yields fell, the investor made a capital gain on both bonds.

(e) When yields fell, the investor made a capital gain on the zero coupon bond but a loss on the 7% semi-annual coupon bond.

Question 230  bond pricing, capital raising

A firm wishes to raise $10 million now. They will issue 6% pa semi-annual coupon bonds that will mature in 8 years and have a face value of $1,000 each. Bond yields are 10% pa, given as an APR compounding every 6 months, and the yield curve is flat.

How many bonds should the firm issue? All numbers are rounded up.

(a) 9,023 bonds

(b) 10,000 bonds

(c) 11,485 bonds

(d) 12,713 bonds

(e) 12,768 bonds

Question 233  bond pricing

A four year bond has a face value of $100, a yield of 9% and a fixed coupon rate of 6%, paid semi-annually. What is its price?

(a) $94.6187

(b) $90.1062

(c) $72.592

(d) $70.3185

(e) $53.1754

Question 255  bond pricing

In these tough economic times, central banks around the world have cut interest rates so low that they are practically zero. In some countries, government bond yields are also very close to zero.

A three year government bond with a face value of $100 and a coupon rate of 2% pa paid semi-annually was just issued at a yield of 0%. What is the price of the bond?

(a) 94.20452353

(b) 100

(c) 106

(d) 112

(e) The bond is priceless.

Question 332  bond pricing, premium par and discount bonds

Bonds X and Y are issued by the same US company. Both bonds yield 6% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond X pays coupons of 8% pa and bond Y pays coupons of 12% pa. Which of the following statements is true?

(a) Bonds X and Y are premium bonds.

(b) Bonds X and Y are discount bonds.

(c) Bond X is a discount bond but bond Y is a premium bond.

(d) Bond X is a premium bond but bond Y is a discount bond.

(e) Bonds X and Y are par bonds.

Question 257  bond pricing

A 10 year bond has a face value of $100, a yield of 6% pa and a fixed coupon rate of 8% pa, paid semi-annually. What is its price?

(a) $114.7202

(b) $114.8775

(c) $122.9398

(d) $126.628

(e) $174.3874

Question 266  bond pricing, premium par and discount bonds

Bonds X and Y are issued by the same company. Both bonds yield 10% pa, and they have the same face value ($100), maturity, seniority, and payment frequency.

The only difference is that bond X pays coupons of 6% pa and bond Y pays coupons of 8% pa. Which of the following statements is true?

(a) Bonds X and Y are premium bonds.

(b) Bonds X and Y are discount bonds.

(c) Bond X is a discount bond but bond Y is a premium bond.

(d) Bond X is a premium bond but bond Y is a discount bond.

(e) Bonds X and Y are par bonds.

Question 287  bond pricing

A 30 year Japanese government bond was just issued at par with a yield of 1.7% pa. The fixed coupon payments are semi-annual. The bond has a face value of $100.

Six months later, just after the first coupon is paid, the yield of the bond increases to 2% pa. What is the bond's new price?

(a) $89.5717

(b) $89.6632

(c) $90.5598

(d) $93.3393

(e) $100.0000

Question 29  interest only loan

You want to buy an apartment priced at $300,000. You have saved a deposit of $30,000. The bank has agreed to lend you the $270,000 as an interest only loan with a term of 25 years. The interest rate is 12% pa and is not expected to change.

What will be your monthly payments? Remember that mortgage payments are paid in arrears (at the end of the month).

(a) 900

(b) 2,700

(c) 2,722.1

(d) 2,843.71

(e) 34,424.99

Question 42  interest only loan

You just signed up for a 30 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 6% pa which is not expected to change.

How much did you borrow? After 15 years, just after the 180th payment at that time, how much will be owing on the mortgage? The interest rate is still 6% and is not expected to change. Remember that the mortgage is interest-only and that mortgage payments are paid in arrears (at the end of the month).

(a) $495,533.92, $349,640.96

(b) $500,374.84, $355,510.54

(c) $500,374.84, $250,187.42

(d) $600,000.00, $600,000.00

(e) $600,000.00, $300,000.00

Question 57  interest only loan

You just borrowed $400,000 in the form of a 25 year interest-only mortgage with monthly payments of $3,000 per month. The interest rate is 9% pa which is not expected to change.

You actually plan to pay more than the required interest payment. You plan to pay $3,300 in mortgage payments every month, which your mortgage lender allows. These extra payments will reduce the principal and the minimum interest payment required each month.

At the maturity of the mortgage, what will be the principal? That is, after the last (300th) interest payment of $3,300 in 25 years, how much will be owing on the mortgage?

(a) $6,766.6469

(b) $35,748.4866

(c) $63,663.4188

(d) $90,000.0000

(e) Nothing, the mortgage will be fully paid off prior to maturity.

Question 107  interest only loan

You want to buy an apartment worth $300,000. You have saved a deposit of $60,000.

The bank has agreed to lend you $240,000 as an interest only mortgage loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?

(a) 17,435.74

(b) 1,438.92

(c) 1,414.49

(d) 1,200.00

(e) 666.67

Question 160  interest only loan

You want to buy an apartment priced at $500,000. You have saved a deposit of $50,000. The bank has agreed to lend you the $450,000 as an interest only loan with a term of 30 years. The interest rate is 6% pa and is not expected to change. What will be your monthly payments?

(a) $ 1,250.00

(b) $ 2,250.00

(c) $ 2,652.17

(d) $ 2,697.98

(e) $ 32,692.01

Question 381  Merton model of corporate debt, option, real option

In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying risk free government bonds and:

(a) Selling the company's assets.

(b) Buying a call option on the company's assets.

(c) Buying a put option on the company's assets.

(d) Selling a call option on the company's assets.

(e) Selling a put option on the company's assets.

Question 382  Merton model of corporate debt, real option, option

In the Merton model of corporate debt, buying a levered company's shares is equivalent to:

(a) Buying the company's assets.

(b) Buying a call option on the company's assets.

(c) Buying a put option on the company's assets.

(d) Buying the company's assets and buying a call option on those assets.

(e) Buying the company's assets and buying a put option on those assets.

Question 383  Merton model of corporate debt, real option, option

In the Merton model of corporate debt, buying a levered company's debt is equivalent to buying the company's assets and:

(a) Selling government bonds.

(b) Buying a call option on the company's assets.

(c) Buying a put option on the company's assets.

(d) Selling a call option on the company's assets.

(e) Selling a put option on the company's assets.

Question 385  Merton model of corporate debt, real option, option

A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:

##V## = Market value of assets.

##E## = Market value of (levered) equity.

##D## = Market value of zero coupon bonds.

##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The levered equity graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?

(a) Label a represents the market value of equity ##(E)## at t=0 on the red curved line or t=1 on the blue crooked line.

(b) Label b represents the market value of equity now ##(E_0)##.

(c) Label c represents the market value of equity if the assets were liquidated right now.

(d) Label d represents the face value of debt at maturity ##(F_1)##.

(e) Label e represents the market value of debt ##(D)## at t=0 on the red curved line or t=1 on the blue crooked line.

Question 386  Merton model of corporate debt, real option, option

A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:

##V## = Market value of assets.

##E## = Market value of (levered) equity.

##D## = Market value of zero coupon bonds.

##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

The risky corporate debt graph above contains bold labels a to e. Which of the following statements about those labels is NOT correct?

(a) Label a represents the market value of equity ##(E)## at t=0 on the red curved line or t=1 on the blue crooked line.

(b) Label b represents the face value of debt at maturity ##(F_1)##.

(c) Label c represents the market value of debt now ##(D_0)##.

(d) Label d represents the face value of debt at maturity ##(F_1)##.

(e) Label e represents the market value of assets ##(V)## at t=0 on the red curved line or t=1 on the blue crooked line.

Question 433  Merton model of corporate debt, real option, option, no explanation

A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:

##V## = Market value of assets.

##E## = Market value of (levered) equity.

##D## = Market value of zero coupon bonds.

##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

What is the payoff to equity holders at maturity, assuming that they keep their shares until maturity?

(a) ##max(V_1 - F_1, 0)##.

(b) ##max(V_1 - D_1, 0)##.

(c) ##max(F_1 - V_1, 0)##.

(d) ##max(D_1 - V_1, 0)##.

(e) ##-min(F_1 - V_1, 0)##.

Question 434  Merton model of corporate debt, real option, option

A risky firm will last for one period only (t=0 to 1), then it will be liquidated. So it's assets will be sold and the debt holders and equity holders will be paid out in that order. The firm has the following quantities:

##V## = Market value of assets.

##E## = Market value of (levered) equity.

##D## = Market value of zero coupon bonds.

##F_1## = Total face value of zero coupon bonds which is promised to be paid in one year.

What is the payoff to debt holders at maturity, assuming that they keep their debt until maturity?

(a) ##\max(V_1 - F_1,0)##.

(b) ##\max(F_1, V_1)##.

(c) ##\max(F_1, 0)##.

(d) ##\min(F_1, V_1)##.

(e) ##\min(V_1-F_1, F_1)##.

Question 384  option, real option

Which of the following is the least useful method or model to calculate the value of a real option in a project?

(a) Project value with the option less project value without the option.

(b) No-arbitrage binomial option pricing model.

(c) Risk-neutral binomial option pricing model.

(d) Gordon growth model.

(e) Black-Sholes option pricing model.

Question 387  real option, option

One of the reasons why firms may not begin projects with relatively small positive net present values (NPV's) is because they wish to maximise the value of their:

(a) Expansion option.

(b) Abandonment option.

(c) Timing (or delaying) option.

(d) Production (or switching) option.

(e) Underlying asset.

Question 388  real option, option

A moped is a bicycle with pedals and a little motor that can be switched on to assist the rider. Mopeds are useful for quick transport using the motor, and for physical exercise when using the pedals unassisted. This offers the rider:

(a) An expansion option.

(b) An abandonment option.

(c) A timing (or delaying) option.

(d) A production (or switching) option.

(e) Lots of options to exercise if they're out-of-money and have no fuel.

Question 389  real option, option

You're thinking of starting a new cafe business, but you're not sure if it will be profitable.

You have to decide what type of cups, mugs and glasses you wish to buy. You can pay to have your cafe's name printed on them, or just buy the plain un-marked ones. For marketing reasons it's better to have the cafe name printed. But the plain un-marked cups, mugs and glasses maximise your:

(a) Expansion option.

(b) Abandonment option.

(c) Timing (or delaying) option.

(d) Production (or switching) option.

(e) Underlying asset.

Question 390  real option, option

Some financially minded people insist on a prenuptial agreement before committing to marry their partner. This agreement states how the couple's assets should be divided in case they divorce. Prenuptial agreements are designed to give the richer partner more of the couples' assets if they divorce, thus maximising the richer partner's:

(a) Expansion option.

(b) Abandonment option.

(c) Timing (or delaying) option.

(d) Production (or switching) option.

(e) Underlying asset.

Question 392  real option, option

An abandonment option is best modeled as a or option?

Question 391  real option, option

An expansion option is best modeled as a or option?

Question 393  real option, option

A timing option is best modeled as a or option?

Question 394  real option, option

According to option theory, it's rational for students to submit their assignments as or as possible?

Question 395  real option, option

The cheapest mobile phones available tend to be those that are 'locked' into a cell phone operator's network. Locked phones can not be used with other cell phone operators' networks.

Locked mobile phones are cheaper than unlocked phones because the locked-in network operator helps create a monopoly by:

(a) Destroying customers' expansion option.

(b) Destroying customers' abandonment option.

(c) Destroying customers' timing (or delaying) option.

(d) Destroying customers' production (or switching) option.

(e) Growing customers' binomial tree.

Question 397  financial distress, leverage, capital structure, NPV

A levered firm has a market value of assets of $10m. Its debt is all comprised of zero-coupon bonds which mature in one year and have a combined face value of $9.9m.

Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.

Therefore the current market capitalisation of debt ##(D_0)## is $9m and equity ##(E_0)## is $1m.

A new project presents itself which requires an investment of $2m and will provide a:

• $6.6m cash flow with probability 0.5 in the good state of the world, and a
• -$4.4m (notice the negative sign) cash flow with probability 0.5 in the bad state of the world.

The project can be funded using the company's excess cash, no debt or equity raisings are required.

What would be the new market capitalisation of equity ##(E_\text{0, with project})## if shareholders vote to proceed with the project, and therefore should shareholders proceed with the project?

(a) $2.5m, so they should vote yes.

(b) $2.045455m, so they should vote yes.

(c) $0.9m, so they should vote no.

(d) $0, so they should vote no.

(e) -$0.9m, so they should vote no.

Question 398  financial distress, capital raising, leverage, capital structure, NPV

A levered firm has zero-coupon bonds which mature in one year and have a combined face value of $9.9m.

Investors are risk-neutral and therefore all debt and equity holders demand the same required return of 10% pa.

In one year the firm's assets will be worth:

• $13.2m with probability 0.5 in the good state of the world, or
• $6.6m with probability 0.5 in the bad state of the world.

A new project presents itself which requires an investment of $2m and will provide a certain cash flow of $3.3m in one year.

The firm doesn't have any excess cash to make the initial $2m investment, but the funds can be raised from shareholders through a fairly priced rights issue. Ignore all transaction costs.

Should shareholders vote to proceed with the project and equity raising? What will be the gain in shareholder wealth if they decide to proceed?

(a) Yes, $3m

(b) Yes, $1.5m

(c) Yes, $1m

(d) No, -$0.5m

(e) No, -$1.5m

Question 102  option, hedging

A company runs a number of slaughterhouses which supply hamburger meat to McDonalds. The company is afraid that live cattle prices will increase over the next year, even though there is widespread belief in the market that they will be stable. What can the company do to hedge against the risk of increasing live cattle prices? Which statement(s) are correct?

(i) buy call options on live cattle.

(ii) buy put options on live cattle.

(iii) sell call options on live cattle.

Select the most correct response:

(a) Only (i) is true.

(b) Only (ii) is true.

(c) Only (iii) is true.

(d) Only (i) and (ii) is true.

(e) All statements (i), (ii) and (iii) are true.

Question 103  option

Below are 4 option graphs. Note that the y-axis is payoff at maturity (T). What options do they depict? List them in the order that they are numbered.

(a) 1: short call, 2: long call, 3: short put, 4: long put.

(b) 1: long call, 2: long put, 3: short call, 4: short put.

(c) 1: short put, 2: long put, 3: short call, 4: long call.

(d) 1: long put, 2: short put, 3: long call, 4: short call.

(e) 1: long put, 2: short call, 3: short put, 4: long call.

Question 122  option

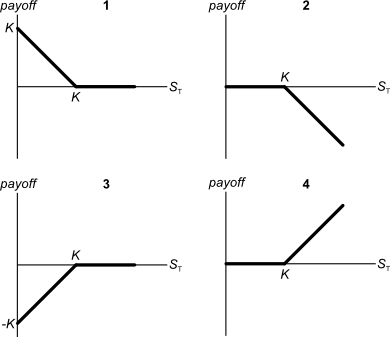
You have just sold an 'in the money' 6 month European put option on the mining company BHP at an exercise price of $40 for a premium of $3.

Which of the following statements best describes your situation?

(a) You have bought the right to buy a BHP share for $40 in 6 months.

(b) You have bought the right to sell a BHP share for $40 in 6 months.

(c) You have bought the obligation to sell a BHP share for $40 in 6 months.

(d) You have sold the right that allows your counterparty to buy a BHP share from you for $40 in 6 months. This means that you have the obligation to sell a BHP share to your counterparty for $40 in 6 months if he wants to buy it.

(e) You have sold the right that allows your counterparty to sell a BHP share to you for $40 in 6 months. This means that you have the obligation to buy a BHP share from your counterparty for $40 in 6 months if he wants to sell it.

Question 123  option

Below are 4 option graphs. Note that the y-axis is payoff at maturity (T). What options do they depict? List them in the order that they are numbered

(a) 1: short call, 2: long call, 3: short put, 4: long put.

(b) 1: long call, 2: long put, 3: short call, 4: short put.

(c) 1: short put, 2: long put, 3: short call, 4: long call.

(d) 1: long put, 2: short put, 3: long call, 4: short call.

(e) 1: short call, 2: long put, 3: long call, 4: short put.

Question 274  derivative terminology, option

The 'option price' in an option contract is paid at the start when the option contract is agreed to. or ?

Question 276  derivative terminology, option

The 'option strike price' in an option contract, also known as the exercise price, is paid at the start when the option contract is agreed to. or ?

Question 304  option

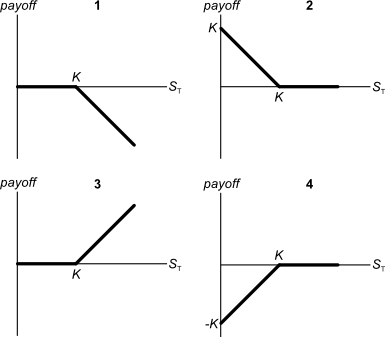
Which one of the following is NOT usually considered an 'investable' asset for long-term wealth creation?

(a) Shares (ordinary and preference stocks).

(b) Real estate (land and buildings).

(c) Options (calls and puts).

(d) Human capital (education)

(e) Debt (bond and loan assets)

Question 334  option

Which option position has the possibility of unlimited potential losses?

(a) Long call options.

(b) Short call options.

(c) Long put options.

(d) Short put options.

(e) No option positions have the possibility of unlimited potential losses.

Question 396  real option, option

Your firm's research scientists can begin an exciting new project at a cost of $10m now, after which there’s a:

• 70% chance that cash flows will be $1m per year forever, starting in 5 years (t=5). This is the A state of the world.
• 20% chance that cash flows will be $3m per year forever, starting in 5 years (t=5). This is the B state of the world.
• 10% chance of a major break through in which case the cash flows will be $20m per year forever starting in 5 years (t=5), or instead, the project can be expanded by investing another $10m (at t=5) which is expected to give cash flows of $60m per year forever, starting at year 9 (t=9). Note that the perpetual cash flows are either the $20m from year 4 onwards, or the $60m from year 9 onwards after the additional $10m year 5 investment, but not both. This is the C state of the world.

The firm's cost of capital is 10% pa.

What's the present value (at t=0) of the option to expand in year 5?

(a) $12.54m

(b) $13.71m

(c) $20.98m

(d) $26.25m

(e) $27.37m

Question 399  option, no explanation

A European call option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.

What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the call option?

(a) ##\max(S_T - K, 0)##.

(b) ##\max(S_T - K, K)##.

(c) ##\max(K-S_T, 0)##.

(d) ##\max(K-S_T, K)##.

(e) ##\min(K-S_T, 0)##.

Question 400  option, no explanation

A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.

What is an expression for the payoff at maturity ##(f_T)## in dollars from owning (being long) the put option?

(a) ##\max(S_T - K, 0)##.

(b) ##\max(S_T - K, K)##.

(c) ##\max(K-S_T, 0)##.

(d) ##\max(K-S_T, K)##.

(e) ##\min(K-S_T, 0)##.

Question 431  option, no explanation

A European put option will mature in ##T## years with a strike price of ##K## dollars. The underlying asset has a price of ##S## dollars.

What is an expression for the payoff at maturity ##(f_T)## in dollars from having written (being short) the put option?

(a) ##\max(S_T - K, 0)##.

(b) ##-\max(S_T - K, 0)##.

(c) ##\max(K-S_T, 0)##.

(d) ##-\max(K-S_T, 0)##.

(e) ##-\min(S_T - K, 0)##.

Question 432  option, option intrinsic value, no explanation

An American style call option with a strike price of ##K## dollars will mature in ##T## years. The underlying asset has a price of ##S## dollars.

What is an expression for the current intrinsic value in dollars from owning (being long) the American style call option? Note that the intrinsic value of an option does not subtract the premium paid to buy the option.

(a) ##\min(S_0 - K, 0)##.

(b) ##\min(K-S_0, 0)##.

(c) ##\max(S_0-K, 0)##.

(d) ##\max(K-S_0, 0)##.

(e) ##\max(K, S_0)##.

Question 435  option, no explanation

Will the price of a call option on equity or if the standard deviation of returns (risk) of the underlying shares becomes higher?

Question 439  option, no explanation

Two call options are exactly the same, but one has a low and the other has a high exercise price. Which option would you expect to have the higher price, the option with the or exercise price, or should they have the price?